当前位置：文档之家 › 有限自动机理论06章图灵机-简化

有限自动机理论06章图灵机-简化

  • 格式：ppt
  • 大小：1.40 MB
  • 文档页数：220

下载文档原格式

  / 220

合集下载

有限自动机理论05章下推自动机(简化)

有限自动机理论05章下推自动机(简化)


接收语言L={(ab)n|n≥0}
< q1，a，Z0，q2，AZ0> < q2，b，A，q1，ε> < q1，ε，Z0，q1，ε > 规则是不确定的。
n 接收语言L={(ab) |n>0}
< q0，a，Z0，q0，AZ0> < q0，b，A，q1，ε> < q1，a，Z0，q2，AZ0> < q2，b，A，q1，ε> < q1，ε，Z0，q1，ε> 规则是不确定的。
NFA：δ(q，x)= {q1，q2，… qn｝ 单态的PDA： <x，q， q1 > <x，q， q2 > … <x，q， qn >
NFA：
若 q ∈δ*(q0，w) 单态的PDA： 有 （*，w，q0）=>*（*，ε，q）
NFA：
若q∈F 则 单态的PDA： <ε，q，ε>
q0∈Q是开始状态 Z0∈Г是栈底符号 FQ是接收状态集合
δ：Q×(∑∪{ε})×Г→Q×Г* 对于确定的PDA，有 δ(q，x，D）=( q′，V) 对于不确定的PDA，有 ( q′，V) ∈δ（q，x，D）
一般
使用 <q，x，D，q′，V> 表示δ函数
定义5-2 PDA格局(或瞬间描述ID) 格局代表某个时刻PDA的情况 PDA的格局是一个三元式 (q，w，ζ)
不确定 PDA 对于某一格局可 能会有不同的下一格局。
+ 用=> 代表格局的多次变换
* 用=> 代表格局的任意次变换
5.1.3 PDA接收语言的两种方式
定义 5-3 PAD 以空栈方式接收的语 言为L(M），且 L(M)={w|(q0，w，Z0) =>*(q ， ε ， ε) q∈Q}
理论计算机科学中的图灵机

理论计算机科学中的图灵机

理论计算机科学中的图灵机图灵机是理论计算机科学中的一个重要概念。

它被认为是能够计算任何可计算问题的最基本的计算机模型。

理解图灵机对于对计算机科学的学习和研究都至关重要。

一、图灵机的定义和原理图灵机是由英国数学家图灵提出的一种计算模型。

它包括一个有限控制器和一条无限长的纸带。

纸带被划分为一系列的单元格，每个单元格上可以写上一个字符。

控制器通过读取纸带上的字符和控制器内部的状态来进行计算。

它可以进行有限的计算，而且可以处理无限长的输入。

在图灵机模型中，所有的操作都是基于读取和写入单元格上的字符来进行。

图灵机具有非常简单的结构，但它却能够计算出任何可计算问题。

二、图灵机的应用图灵机能够计算出任何可计算问题，因此它在理论计算机科学中有着非常重要的应用。

它被用于证明计算机科学中的许多重要问题，例如停机问题和可计算性问题。

通过证明一个问题是不可计算的，我们可以得出它是无法用计算机解决的。

这对于计算机的设计和实现都有着重要的指导意义。

此外，图灵机还被广泛应用于计算机语言和自动机理论的研究中。

我们可以使用图灵机来描述计算机语言的语法和语义，并且使用它来定义自动机模型。

这在编程语言的编译、解释和分析中都有着广泛的应用。

三、图灵机的限制尽管图灵机是一种非常强大的计算模型，它仍然存在着一些限制。

其中最明显的一点是图灵机的速度。

尽管图灵机能够计算出任何可计算问题，但某些问题可能需要非常长的时间才能得到结果。

例如，计算出一个长文本的哈希值可能需要几分钟，而对于一个复合的问题，甚至需要几个世纪才能计算得出。

此外，图灵机还无法解决某些问题，例如非计算问题和不规则问题。

这些问题之所以无法用图灵机解决，是因为它们没有确定的方法来解决它们。

这些问题是无法用算法来解决的，并且需要人类直接进行解决。

四、结语图灵机是理论计算机科学中最重要的概念之一。

它被认为是能够计算出任何可计算问题的最基本计算机模型。

通过图灵机的研究，我们可以深入理解计算机科学的基本原理，理解计算机能力和限制。

图灵机计算机的理论模型

图灵机计算机的理论模型


图灵机——计算机的理论模型
机器的程序是五元组｛Si , X , Y , L(R或N) , Sj｝形式的指 令集，定义了机器在一个特定状态下读入一个特定字符时所 采取的动作。 五个元素的含义如下：
①Si 表示机器当前的状态；
②X 表示机器从方格中读入的内容，也即当前内容； ③Y 表示机器用来代替X 写入方格中的内容； ④L、R、N 分别表示左移一格、右移一格和不移动； ⑤Sj 表示机器下一步的状态。
图灵机——计算机的理论模型
图灵机的计算开始于初始状态，设为S0，终止于停止（HALT）状态，设为SH。 例: 设计能够实现“a+1”运算的图灵机，计算完成后要求读写头回到原位。
图灵机进行“a+1”运算的控制规则表
输入
当前状态 （Si） S0 S1 S1 S1 S2 S2 S2 S3 S3 S3 S4 当前内容 （X ） b 0 1 b 0 1 b 0 1 b 任意 重写的新内容 （Y） b 1 0 b 1 0 1 0 1 b b
英国科学家阿兰.图灵 （1912-1954）
图灵证明，只有图灵机能解决的 计算问题，实际计算机才能解决。
“图灵奖”是美国计算机协会于1966年设立的。
什么是图灵机？ 图灵机由一条无限长的纸带、读/写头及控制
器构成。
图灵机模型
控制器内包括控制规则表，它能够通过读/写头对纸带上 的符号进行读或写，读写头可以在纸带上左右移动。 纸带分成了一个个的小方格，每个方格中可以记录机器 字母表里的符号，如0或1等。
பைடு நூலகம்输出
读写头移动方向 （L，R或N） L R L R R L L R R N R 进入的新状态 （Sj） S1 S3 S2 SH S3 S2 S4 S3 S3 SH S3
turingmachine图灵机

turingmachine图灵机

图灵机的基本思想 图灵机的组成 图灵机的计算思想
图灵机的意义
图灵机模型理论是计算科学最核心的理论之一 图灵机模型为计算机设计指明了方向 图灵机模型是算法分析和程序语言设计的基础
理论
图灵机概述
所谓的图灵机就是指一个抽象的机器，它有 一条无限长的纸带，纸带分成了一个一个的 小方格，每个方格有不同的颜色。有一个机 器头在纸带上移来移去。机器头有一组内部 状态，还有一些固定的程序。在每个时刻， 机器头都要从当前纸带上读入一个方格信息， 然后结合自己的内部状态查找程序表，根据 程序输出信息到纸带方格上，并转换自己的 内部状态，然后进行移动。
读写头
状态控制器
图灵机的组成
一个确定型单带图灵机由以下四个部分组成 (见上页图)： ·无限长的带子 TAPE，带子划成小格， 格子标记 … , －3，－2，－1，0，1，2, 3，… ·读写头HEAD ·控制规则表TABLE ·状态存储器
图灵机的组成-TAPE
纸带被划分为一个接一个的小格子，每个格 子上包含一个来自有限字母表的符号，字母 表中有一个特殊的符号 表示空白。纸带上 的格子从左到右依此被编号为 0, 1, 2, ... ， 纸带的右端可以无限伸展。
图灵机的基本思想
用机器来模拟人们用纸笔进行数学运算的过 程，该过程可分为如下两个简单动作：
➢在纸上写上或擦除某个符号 ➢把注意力从纸的一个位置移动到另一个位置
而在每个阶段，人要决定下一步的动作，依 赖于：
➢此人当前所关注的纸上某个位置的符号 ➢此人当前思维的状态。
… －2 －1 0 1 2 3 …
图灵机计算思想
计算机系统应该有： 存储器（相当于存储带）
中央处理器（控制器及其状态）
为了能够将数据保存到存储器并将计算结 果从存储器送出来展示给用户，计算机系 统还应该有输入设备和输出设备如键盘、 鼠标、显示器和打印机等。
高级语言及其语法描述-有限自动机理论

高级语言及其语法描述-有限自动机理论


文法G2对句子aaabb的推导： S => A B S A B => a A B A a A => a a A B A a A => a a a B A a => a a a b B B b B => a a a b b B b
27
e.g. 文法产生的语言
S a S b | ab
文法G3对句子aaaabbbb的推导： S => a S b S a S b => a a S b b S a S b => a a a S b b b S a S b => a a a a b b b b S a b
E (E) (E+E) (i+E) (i+i)
17
+ ，从 出发，经一步或若干步，可 1 n 1 推导出n， ≥1 ，从 出发，经0步或若干步，可推 1 n 1 导出n ， ≥0 + 故1n，相当于=或
18
三种推导的比较
• 直接推导（）的长度为1 • 直接推导序列（ +）的长度n≥1 • 广义推导（ *）的长度≥0
7
得到语法分析树: <句子> <主语> <代词> <谓语> <间接宾语> <动词> <直接宾语> <名词>
<代词> <冠词>
He
gave
me
a
book
8
• 上下文无关文法的定义： 一个上下文无关文法G是一个四元式 G=(VT，VN，S，P)，其中
–VT：终结符集合(非空) –VN：非终结符集合(非空)，且VT VN=
形式化的方法
图灵和图灵机模型PPT课件

图灵和图灵机模型PPT课件

– 而自动计算机的理论模型则是图灵在其论文的一个脚注中“顺便”提出 来的。这真可谓“歪打正着”——图灵这篇传世的论文主要是因为这个 脚注，其正文的意义和重要性反而退居其次了。
15
第十五页，共24页。
图灵简介
• 随后，应邀于美国普林斯顿大学与美国著名 数学家和逻辑学家邱奇合作，并于1938年取 得博士学位。在这里，还研究了布尔1854年 创建的逻辑代数，自己动手用继电器搭建逻 辑门，组成了乘法器。在美国，还遇到了普 林斯顿大学教师天才科学家冯·诺伊曼。
– 1946年5月以前由于找不到称心的助手，一直“单枪匹马”，直到威尔 金森（1970年图灵奖获得者）成了图灵得力助手，此时ACE已到第5版， 前4版由于图灵不善于也不重视保管文档资料而不知去向。
– ACE是一种存储程序式计算机，但其存储程序思想并非受冯·诺伊曼论文的影响，而 是他自己的构思。冯·诺伊曼本人也从来没有说过存储程序的概念是他的发明，却不 止一次地说过图灵是现代计算机设计思想的创始人。
– 图灵机
– 几何定理的机器证明
• 对计算本质的真正认识取决于形式化研究的进程
2
第二页，共24页。
形式化研究进程
• 1275年，思维机器“旋转玩具” 是一种形式化的产物，标志着形式 化思想革命的开始
• 形式化方法和理论的研究学的重要基础 – 希尔伯特纲领：将每一门数学的分支构成形式系统或形式理论，并在以此
– 反映了计算学科的抽象、理论和设计3个过程
• 抽象和理论两个过程关心的是解决具有能行性和有效性 的模型问题
• 设计过程关心的是模型的具体实现问题
10
第十页，共24页。
从计算角度认知思维、视觉和生命过程
• 符号主义者认为：认知是一种符号处理过程， 因此思维就是计算（认知就是计算）
形式语言与自动机理论--第六章(蒋宗礼)

形式语言与自动机理论--第六章(蒋宗礼)


• 右句型(right sentencial form)
–最右派生得到的句型可叫做右句型。
• 最左归约(leftmost reduction)
–与最左派生对相的归约叫做最右归约。
6.1.1 上下文无关文法的派生树
• 规范派生(normal derivation)
–最右派生。
• 规范句型(normal sentencial form)
• 必要性
–设Anα ，现施归纳于派生步数n，证明存在结果为α 的A-子树。 设n≤k(k≥1)时结论成立，往证当n=k+1时结论也成立：令 Ak+1α，则有： AX1X2…Xm *α1X2…Xm *α1α2…Xm … * α 1 α 2 … α m
6.1.1 上下文无关文法的派生树
6.1.1 上下文无关文法的派生树
• CSL
– CSG、LBA。
教材及主要参考书目
1.蒋宗礼，姜守旭. 形式语言与自动机理论. 北京： 清华大学出版社，2003年 2. John E Hopcroft, Rajeev Motwani, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation (2nd Edition). Addison-Wesley Publishing Company, 2001 3. John E Hopcroft, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation. Addison-Wesley Publishing Company, 1979
6.1.1 上下文无关文法的派生树
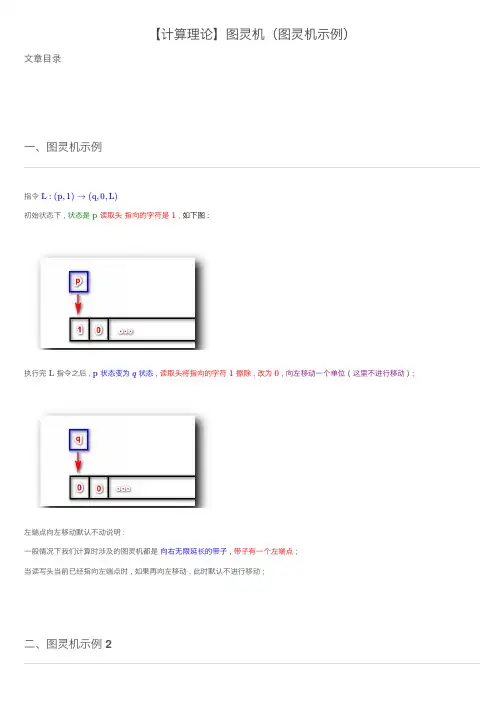
【计算理论】图灵机（图灵机示例）

【计算理论】图灵机（图灵机示例）

【计算理论】图灵机（图灵机⽰例）⽂章⽬录⼀、图灵机⽰例指令 初始状态下 , 状态是 读取头 指向的字符是 ,如下图 :执⾏完 指令之后 , 状态变为 状态 , 读取头将指向的字符 擦除 , 改为 ,向左移动⼀个单位 ( 这⾥不进⾏移动 ) ;左端点向左移动默认不动说明 :⼀般情况下我们计算时涉及的图灵机都是 向右⽆限延长的带⼦ , 带⼦有⼀个左端点 ;当读写头当前已经指向左端点时 , 如果再向左移动 , 此时默认不进⾏移动 ;⼆、图灵机⽰例 2L :(p,1)→(q,0,L)p 1L p q 10任务 : 设计⼀个图灵机 , 给定输⼊之后 , 图灵机会 在输⼊中寻找 字符 ;算法 :如果 找到了 字符 , 就会将该字符转变成 字符 , 然后将当前状态改为接受状态 , 然后停下来 ;如果带⼦上的字符都读取完毕后 , 没有找到 , 只找到了空⽩字符 , 将该空⽩字符改为 , 然后向左移动⼀格 , 然后停下来 ;( ⾃动机停下的前提是处于可接受状态 )根据上述算法 , 构造图灵机 ;图灵机设计 :① 状态集 , 其中 是开始状态 , 是接受状态 ;② 输⼊字符集 ;③ 带⼦字符集 , 其中 是空⽩字符 ;④ 指令 ⑤ 指令 ⑥ 指令 上述图灵机设计中 , 最关键的部分是三条指令 ;图灵机处于开始状态 , 读头指向 字符 , 左端的 是输⼊字符 , 查看图灵机是否接受 字符串 ;下⾯图灵机后续都是空⽩字符 ;根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;如下图 :110f 11Q ={q,f}q f Σ={0,1}Γ={0,1,B}B δ(q,0)=(q,0,R)δ(q,1)=(f,0,R)δ(q,B)=(q,1,L)q 00000B δ(q,0)=(q,0,R)q 0q,0,R q 0此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;如下图 :此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向左移动⼀个字符 ;如下图 :δ(q,0)=(q,0,R)q 0q,0,R q 0δ(q,B)=(q,1,L)q B q,1,L q 1此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;如下图 :此时继续 根据指令 指令 , 当前状态 , 当前指向字符 , 输出内容是 ,即 状态变为 , 读头指向的字符变为 , 向右移动⼀个字符 ;此时的状态 是接受状态 , ⾃动机停⽌运⾏ ;如下图 :δ(q,0)=(q,0,R)q 0q,0,R q 0δ(q,1)=(f,0,R)q 1f,0,R f 0f图灵机 与 ⾃动机 接受的条件是不同的 ;图灵机计算过程中 , ⼀旦到达接受状态 , ⽴刻停机 , 不再继续进⾏计算 ; 并且称该图灵机是可接受的 ;⾃动机即使到达接受状态 , 也要把⾃动机读取的字符读取完毕 , 才停⽌计算 ; 然后在查看最终的状态是否是接受状态 ;。

有限自动机理论CH6

有限自动机理论CH6

w1qw2∈ (∑′)*Q(∑′)* w1是读/写头左边带上的符号串 q是图灵机当前所处的状态 w2是还未扫描到的带上的符号串
2020/1/17
δ(q，x) • 图灵机在格局w1qw2时停机 若w1qw2=w1qxw对于? 无定义。
2020/1/17
定义6-3 格局的转换
• 若M在w1qw2上不停机，则如下定义 格局的转换：
将δ记为一般形式： <q，x，q′，W，{L，R，N}>
2020/1/17
或 图灵机是一个七元组
TM = (Q， ， ， ， q0，B， F) F Q 终止状态集合； 是带符号集合； B 称为空白符； : Q Q {R, L,N}
2020/1/17
定义6-2 图灵机的格局ID
• 若δ（q，x）=( q′，x′，N)，则 r1yqxr2=> r1yq′x′r2
• 若δ（q，x）=( q′，x′，R)，则 r1yqxr2=> r1y x′q′r2
2020/1/17
使用=>+代表格局的多次变换 使用=>*代表格局的任意次变换
2020/1/17
定义6-4
• 图灵机M=（Q，∑， q0， qα，δ ）在字母表∑上接收的语言为 L(M)，则 L(M)={w|存在w1，w2∈(∑′)* 有q0w =>*w1qαw2 }
2020/1/17
∑′={0，1，B}
<q0，0，q0，0，R> <q0，1，q1，1，R> <q1，0，q1，0，R> <q1，B，q2，B，N>
<q1，B ?
2020/1/17
例6-4 构造图灵机
接收语言{ anbn|n>0}
《有限自动机》课件

《有限自动机》课件

并行有限自动机
这种自动机可以在多个处理器上并行运行，从而大大提高了处理速 度。
有限自动机的优化
最小化有限自动机
通过消除不必要的状态和转换，可以创建一个更小、更有效的有 限自动机。这有助于减少计算时间和空间需求。
压缩有限自动机
通过使用更紧凑的数据结构来表示有限自动机，可以减少存储需求 并提高处理速度。
03
描述了状态之间的转移关系。
正则语言与有限自动机的关系
正则语言
由有限自动机识别和生成的语言。
封闭性
正则语言集合在有限自动机上具有封闭性，即任何正则语言的字 符串都可以被有限自动机接受或生成。
识别和生成
有限自动机既可以用来识别正则语言中的字符串，也可以用来生 成正则语言中的字符串。
04
有限自动机的实现与应用
4 有限自动机的理论问题
探讨了有限自动机未来的发展方向，如可变状态和概率 有限自动机等。
有限自动机的分类
总结词
有限自动机的分类
详细描述
有限自动机可以根据不同的分类标准进行分类，如根据状态转换是否依赖于输入，可以分为确定有限 自动机和不确定有限自动机；根据状态转换是否带记忆，可以分为无记忆有限自动机和有记忆有限自 动机。
有限自动机在计算机科学中的应用
总结词
有限自动机在计算机科学中的应用
并行有限自动机
如上所述，通过并行处理可以大大提高有限自动机的处理速度。
有限自动机与其他模型的关系
图灵机
图灵机是理论上最强大的计算模型， 而有限自动机是其最简单的实例。图 灵机的所有操作都可以用有限自动机 模拟。
状态机
状态机是有限自动机的一种特殊形式 ，它只包含两种状态：接受和拒绝。 状态机的应用包括硬件设计和网络协 议。
有限自动机理论习题册-有限自动机原理

有限自动机理论习题册-有限自动机原理


班级 修课人数 )
2016 级 100
)；学位课 (√ )；专业核心课( )；任选课（ ) ） ； ） ； ） ；公选课( )；
课程类型
选修
理论课(√ )；实践课(
课堂讲授为主（ √ ） ；实验为主（ 授课方式 自学为主（ 其他： 考 试( √ )考 查( √ ) ） ；专题讨论为主（
是否采用 多媒体授课
。
10 第 5 章 下推自动机
有限自动机理论
作业
2016.09
第六章 图灵机
I. 构造单道图灵机识别语言 |
11 第 6 章 图灵机
有限自动机理论
作业
2016.09
II. 构造单道图灵机接收语言
|,
12 第 6 章 图灵机
有限自动机理论
作业
2016.09
III. 构造单道图灵机接收语言
|,
13 第 6 章 图灵机
是
考核方式及 成绩构成 学时分配 教材
考试成绩构成及比例：作业 20%+期末 80% 考查成绩构成及比例：作业 100% 讲授 40 学时； 名称 作者
是否采用 双语教学
否
出版社及出版时间
有限自动机理论 2 版
陈文宇、 田玲、 程伟、 刘贵松
电子工业出版社，2013
形式语言与自动机理论 (第 2 版) 形式语言与自动机 参考书目 Introduction to Automata Theory, Languages and Computation. Introduction to the theory of computation. 授课时间
16 第 6 章 图灵机
(8) 所有包含 3 个连续 0 的串。
2 第 2 章 形式语言

离散数学中的有限状态机和图灵机

离散数学是数学的一个分支，它研究的是离散的、离散化的对象和其相关的结构和性质。

其中，有限状态机和图灵机是离散数学中非常重要的概念之一。

有限状态机（Finite State Machine，FSM）又称有限状态自动机，是一种能够自动地进行状态转换的数学模型，它由一组状态、一组输入符号和一组状态转移函数组成。

有限状态机具有有限个状态和可以改变状态的输入符号，它根据输入和当前状态来确定下一个状态以及所执行的动作。

有限状态机的基本组成包括：状态集合、输入符号集合、输出符号集合、状态转移函数和输出函数。

其中，状态集合是有限的，每个状态都有一个或多个输入符号和对应的动作，而状态转移函数表达了从一个状态到另一个状态的转变。

输出函数则定义了在状态转移过程中，输出的对应动作。

有限状态机广泛应用于各个领域，例如自动控制系统、电子电路的设计、编译器、自然语言处理等。

它们通过对输入符号的分析，根据当前状态确定下一个状态并执行相应的动作。

因此，有限状态机是一种简便而有力的数学工具，有助于解决实际问题。

与有限状态机相对应的是图灵机（Turing Machine），它是在理论计算机科学领域中提出的一种抽象模型。

图灵机由一条无限长的纸带、一个读写头和一套指令集组成。

纸带被划分为无限个格子，每个格子上可以写入一个符号，读写头可在不同格子间移动，并根据当前状态和读写头所指格子上的符号来确定下一步的动作。

图灵机具备了无限的纸带和可执行的指令集，在理论上能够实现任何计算过程。

它是经典计算机科学理论中最重要的抽象计算模型之一，对计算机科学的发展起到了巨大的推动作用。

有限状态机和图灵机在离散数学中的研究和应用，对计算理论、自动机理论和形式语言等领域都具有重要影响。

它们帮助我们理解计算机程序的运行原理、设计和分析自动化系统、解决问题等。

总之，离散数学中的有限状态机和图灵机是两个重要的概念，它们分别对应了离散系统和通用计算机。

有限状态机可以方便地描述和分析各种状态转换的问题，而图灵机则提供了一种抽象的计算模型，帮助我们理解计算的本质和计算机的工作机制。

四种自动机与对应文法 有限自动机 下推自动机 图灵机 线性有界自动机


语言及其表示
➢ 串的连接（concatenation）运算
设 x 和 y 是两个串，xy 称为串 x 和串 y 的连接，用 x • y表示
x • y xy
例 设 x aba y cb 则 x • y aba • cb abacb 易知：1）对任意一个串 x ,都有
x• •x x 2）若 z x • y，则
语言理论
语言
自然语言 人工语言
自然语言：人与人之间交流的基本手段。 如：汉语、英语、俄语、法语、…等
人工语言：主要用于人与计算机之间的交流。
如：程序设计语言
语言理论
形式语言：研究自然语言和人工语言都必须遵循的一般规律 研究字符串集合及其性质的学科
Chomsky文法体系：4种类型的文法及其产生的语言 正规文法RG——正规语言RL； 上下文无关文法CFG——上下文无关语言CFL； 上下文有关文法CSG——上下文有关语言CSL； 无限制文法URG——递归可枚举语言r.e.。
语言及其表示
4） 不含变量的句型称为句子。 5） 若对文法 G 存在下面的多步推导
1
G
2
,
2
G
3,
,
n1
G
n
*
则可简记为
1
G
n
。
注：① 上述“多步推导”是一个泛称，它也可以表示 0 步推导
（当 n=1 时）
②在不会产生混淆的情况下，中的 G 可以省略。 G
➢文法所产生的语言
设 G=(V, T; P, S)为一个文法，那么 G 所产生的语言为
因此， L2 也称为字母表{a,b}上全体回文的集合。易知它是一个无 限集。
语言及其表示
对于语言，有 3 种特例要特别注意：

图灵机的原理

图灵机的原理图灵机是英国数学家艾伦·图灵于1936年提出的一种抽象的数学模型，用来描述一种能够模拟任何计算机算法的理论计算机。

图灵机的原理是基于一种简单的计算模型，它包括一个无限长的纸带和一个能够读写纸带上符号的读写头，以及一系列状态和状态转移规则。

图灵机的设计思想和工作原理对于理解计算机科学的基本概念和原理具有重要的意义。

图灵机的核心是其状态转移规则，它描述了在给定状态下，图灵机应该如何根据当前读取的符号和内部状态来进行下一步的操作。

这种简单的状态转移规则使得图灵机能够模拟任何可以被算法描述的计算过程，从而成为了计算理论的基础模型之一。

图灵机的工作原理可以简单描述为，读写头在纸带上移动，读取当前符号并根据当前状态和读取的符号进行状态转移，然后根据状态转移规则进行下一步操作。

这个过程不断重复，直到图灵机进入停机状态或者无限循环。

图灵机的原理具有重要的理论意义，它证明了存在一种通用的计算模型，能够模拟任何可以被算法描述的计算过程。

这个理论结果被称为“图灵完备性”，它表明只要一种计算模型具有和图灵机相同的能力，就能够模拟任何计算过程。

这也是为什么图灵机被认为是计算机科学的基础理论之一。

除了理论意义，图灵机的原理还对计算机科学和人工智能领域有着重要的启发作用。

图灵机的设计思想和工作原理启发了人们对计算机和算法的理解，也为人工智能的发展提供了重要的理论基础。

图灵机的原理对于理解计算机科学的基本概念和原理具有重要的意义。

总的来说，图灵机的原理是计算机科学领域中非常重要的理论概念，它描述了一种能够模拟任何计算机算法的理论计算机模型。

图灵机的工作原理基于简单的状态转移规则，能够模拟任何可以被算法描述的计算过程，具有重要的理论意义和启发作用。

图灵机的原理对于理解计算机科学的基本概念和原理具有重要的意义，也为人工智能的发展提供了重要的理论基础。

确定有限自动机的化简

确定有限自动机的化简非确定有限自动机确定有限自动机确定有限状态自动机非确定性有限自动机确定性有限自动机非确定有限状态自动机不确定的有限自动机确定的有限自动机不确定有限自动机
确定有限自动机的化简
一、准备知识
引论一：s1、s2是S中的两个等价状态，a 是符号表Σ中的一个符号，如果δ(s1,a)存在， 则δ(s2,a)亦存在，且δ(s1,a)与δ(s2,a)等价。 引论二：s1、s2是S中的两个状态，对Σ中 任意符号a，如果δ(s1,a)存在，则δ(s2,a)必存在 且二者等价，则s1与s2等价。 引论三：如果A、B是S中的两个子集，且 A与B中状态两两不等价，则对Σ中的一个符号a， δ-1(A,a)与δ-1(B,a)中状态两两不等价。
二、确定有限自动机的化简
1、令A1=F（终止状态集）、A·=S-A1。 则A1与A2之状态两两不等价。 2、设已构造出A1、A2、……、Ak，对任 意的i,j，Ai与Aj中状态两两不等价，对任意的符 号a，则δ-1(Ai,a)∩Aj，i,j=1,2,3,……,k中任两个 状态子集中状态是两两不等价。 3、重复2直到状态集数不增加止，则每一 个状态集中任两个状态等价。将等价状态合并 成一个状态，即为简化的DFA。
6}。 。
得如下分划π： 得如下分划 ： 1பைடு நூலகம்{0}， ， 4={3，4，5，6}。 ， ， ， 。
2={1}， ，
3={2}， ，
简化后的确定有限自动机如下： 简化后的确定有限自动机如下：
a 0 b a 2
1 b
a
3 b
词法分析器自动生成
Lex语言定义： 辅助定义式 %% 识别规则 %% 用户子程序
三、举例
将下面不确定有限自动确定化并化简成最简型

图灵机


基本思想
图灵机 图灵的基本思想是用机器来模拟人们用纸笔进行数学运算的过程，他把这样的过程看作下列两种简单的动作： 1、在纸上写上或擦除某个符号； 2、把注意力从纸的一个位置移动到另一个位置。 而在每个阶段，人要决定下一步的动作，依赖于 (1)此人当前所的纸上某个位置的符号和(2)此人当前思维 的状态。 为了模拟人的这种运算过程，图灵构造出一台假想的机器，该机器由以下几个部分组成： 1、一条无限长的纸带 TAPE。纸带被划分为一个接一个的小格子，每个格子上包含一个来自有限字母表的符 号，字母表中有一个特殊的符号表示空白。纸带上的格子从左到右依此被编号为 0，1，2，...，纸带的右端可 以无限伸展。 2、一个读写头 HEAD。该读写头可以在纸带上左右移动，它能读出当前所指的格子上的符号，并能改变当前 格子上的符号。 3、一套控制规则 TABLE。
通用
对于任意一个图灵机，因为它的描述是有限的，因此我们总可以用某种方式将其编码为字符串。我们用表示 图灵机 M的编码。
我们可以构造出一个特殊的图灵机，它接受任意一个图灵机 M的编码，然后模拟 M的运作，这样的图灵机称 为通用图灵机(Universal Turing Machine)。现代电子计算机其实就是这样一种通用图灵机的模拟，它能接受 一段描述其他图灵机的程序，并运行程序实现该程序所描述的算法。但要注意，它只是模拟，因为现实中的计算 机的存储都是有限的，所以无法跨越有限状态机的界限。经典图灵机及其许多变形识别语言的能力都是相同的， 正因为如此，图灵机可以作为计算的一般模型。另外，通用图灵机 (可编程图灵机)是存在的，通用图灵机可以 模拟任意一个图灵机，这也是将图灵机作为现代计算机的形式模型的根本原因。
工作原理
一台图灵机是一个七元组，{Q，Σ，Γ，δ，q0，qaccept，qreject}，其中 Q，Σ，Γ都是有限集合，且 满足：

《有限状态自动机》课件

正则表达式能够表示有限状态自动机，可以 将正则表达式转换为等价的自动机。
2 自动机到正则表达式
通过状态合并和消除，可以将自动机转换为 等价的正则表达式。
有限状态自动机的应用领域
1
计算机科学
在编译器设计、正则表达式匹配和模式
通信技术
信息的
可靠性和准确性。
3
自动控制系统
应用于机器人、交通信号灯和智能家居 等自动控制领域。
总结和展望
总结当前成果
有限状态自动机是描述状态转换的强大工具，已在众多领域取得卓越成就。
研究领域的挑战
仍有待深入研究的问题包括复杂性分析、优化算法和自动机的形式化验证。
未来的发展方向
将有限状态自动机与人工智能、机器学习和量子计算等前沿技术结合，进一步拓展应用领域。
《有限状态自动机》PPT 课件
有限状态自动机（Finite State Machine）是一种能够读取一串输入符号并根 据预设的规则进行状态转换的数学模型。
有限状态自动机的基本概念和定义
状态和转移
有限状态自动机由一组状态 和转移函数组成，通过输入 触发状态之间的转移。
输入和输出
自动机根据输入符号的序列 执行状态转换，并可以产生 相应的输出。
确定性与非确定性
确定性自动机有唯一的下一 个状态，而非确定性自动机 可以有多个可能的下一个状 态。
有限状态自动机的类型
Mealy机
输出与状态转移同时发生，适用于输入输出直接相 关的情况。
Moore机
输出与状态转移分离，适用于输入输出之间有延迟 的情况。
有限状态自动机与正则表达式的关系
1 正则表达式到自动机
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

使用=>+代表格局的多次变换 使用=>*代表格局的任意次变换
定义6-4
图灵机 M= （ Q ， ∑，
q 0 ， qα ， δ ） 在字母表 ∑ 上接收的语言为 L(M) ， 则 L(M)={w|存在w1，w2∈(∑′)* 有 q0w =>* w1qαw2 }
定义6-5 完全的图灵机
如果图灵机对于一切输入串都能够停 机----完全的图灵机。 完全的图灵机接收的语言 L 称为递归 语言(图灵可判定语言)
③在 seek_a 状态时，没有再发现 a ，需 检查是否所有的b都已经被扫描过。 <seek_a，$，check，$，R> <check，$，check，$，R> <check，B，accept，B，N>
某些不需要定义的规则 <start，b，? > //无a
<start，B，? > //无a 无b <del_b，B，? > //b少 <seek_a，B，? > //无b <seek_a，b，? > //不可能 <check，b，? > //b多
6.1 图灵机的基本模型
6.1.1 图灵机的定义
图灵机的物理模型
a1 a2 a3 … aj … an an+1 …
FSC
一个有限状态控制器(FSC) 一个外部的存储设备 可以向右扩展的无限长度带 带上具有左端点，使用“┣”表示 图灵机直接扫描输入带上左端点右边 的第一个符号。
带分解为单元，每个单元可以为 空或存放字母表上的字母符号 带的空白单元标记为B 有限状态控制器通过一个读/写头 与带进行耦合。
②处于状态 del_b ，扫描到 b ，用 # 代替 它，向左寻找a，（从①重复循环） <del_b，b，seek_a，#，L> <seek_a，#，seek_a，#，L> <seek_a，a，del_b，#，R> //最右的a
③seek_a状态时，没有再发现 a(都已被 # 所代替 ) ，还需要检查是否所有的 b 都已经被扫描过。 <seek_a，├，check， ├ ，R> <check，#，check，#，R> <check，B，accept，B，N>
②处于状态 del_b ，扫描到 b ，用 $ 代替 它，向左寻找a，（从①重复循环） <del_b，b，seek_a，$，L> <seek_a， $，seek_a， $ ，L> <seek_a， # ，seek_a， # ，L> <seek_a，a，del_b，#，R>
③在 seek_a 状态时，没有再发现 a （都 已经被#所代替） 需检查是否所有的b都已经被扫描过 还必须注意#与$的顺序。
指令
<start，a，s_a，a，R> <s_a，a，s_a，a，R> (扫描a) <s_a，b，s_b，b，R> <s_b，b，s_b，b，R> (扫描b) <s_b，B，first，B，L> <first，b，first，b，L> <first，a，first，a，L>
已经保证顺序 <first，┣，new_start，┣，R> (开始检查a和b的个数是否相等) <new_start，a，del_b，#，R> <del_b，a，del_b，a，R> <del_b，#，del_b，#，R> <del_b，b，seek_a，#，L>
<seek_a，#，seek_a，#，L> <seek_a，a，del_b，#，R> <seek_a，┣，check，┣ R> （检查是否有多余的b） <check，#，check，#，R> <check，B，accept，B，N>
例6-8接收语言{
TM=（Q，∑，
n n n a b c |n>0｝
五元式描述动作
<q，x，q′，W，{L，R，N}> 其中：x，W∈∑ ′（ ∑的增广集合） 图灵机处于状态q，扫描到符号x， 则 状态变换为q′，印刷上新的符号W， 读/写头向左、或向右 或不移动。
例6-1 用TM接收 语言{a2n |n≥0}
图灵机带上符号串为： ┣aaa…aaaB 图灵机初始处于状态even，将要扫描 第一个a，则
<check2 ，!，check3,! ,R> 识别第一个! <check3 ，! , check3, ! , R> 跳过剩余! <check3 , B , accept , B , N>
<seek_a，┣，check1，┣，R> <check1，#，check1，#，R> <check1，$，check2，$，R> <check2，$，check2 ，$，R> <check2，B，accept，B，N>
例6-6 {
n n a b |n>0}的第二种算法
当图灵机遇到a时，将a改写为# 向右寻找b，找到b，将b改写为$
思路1：
当图灵机遇到a时，将a改写为#
向右寻找b，找到b，将b改写为# 再向左找a … 直到所有a都找完。 (向左找的a是整个a串最左边的a)
指令为 ①读到一个a，用#代替它，向右找b <start，a，del_b，#，R> <del_b，a，del_b，a，R> <del_b，#，del_b，#，R>
再向左找a (此时的a是整个a串最左边的a) …，直到所有a都找完。
指令
①读到一个a，用#代替它，向右寻找b <start，a，del_b，#，R> <del_b，a，del_b，a，R> <del_b，$，del_b，$，R>
②处于状态 del_b ，扫描到 b ，用 $ 代替， 向左寻找a，（从①重复循环） <del_b，b，seek_#，$，L> <seek_#，$，seek_#，$，L> <seek_#，a，seek_#，a，L>//跳过a串 <seek_#，#，seek_a，#，R> //最右# <seek_a，a，del_b，#，R> //最左a
6.1.2 图灵机的构造
例６-３接收仅有一个1的0、1串 TM=({q0，q1，q2},{0，1}, q0，q2,δ)
∑′={0，1，B}
<q0，0，q0，0，R> <q0，1，q1，1，R> <q1，0，q1，0，R> <q1，B，q2，B，N>
例6-4 构造图灵机
接收语言{ anbn|n>0}
②处于状态 del_b时,扫描到b，用 $代替 它，向右寻找c： <del_b , b , del_c , $ , R> <del_c , b , del_c , b , R> <del_c , $ , del_c , $ , R> <del_c ,! , del_c ,! , R>
③处于状态del_c时，扫描到c，用!代替 它，向左找a，(从①开始又重复循环) <del_c ， c , seek_a ，! ，L> <seek_a ，! ， seek_a，!，L> <seek_a ，b ，seek_a , b , L> <seek_a ，$ ，seek_a , $ , L> <seek_a ，# ，seek_a , # , L> <seek_a ，a ，del_b , # , R>
问题
该图灵机能接收anbn的所有串
但该图灵机也能接收aababb 等 原因：使用#代表已扫描的a和b 没有保证a和b的顺序。
为了区别原来的字母a和b
使用#和$分别代替字母a和b 当a和b都识别后，带上的串为 ├###…##$$$…$$B
例6-5 修改上例： ①读到一个a，用#代替它，向右寻找b <start，a，del_b，#，R> <del_b，a，del_b，a，R> <del_b，#，del_b，#，R> <del_b，$，del_b，$，R>
在某个时刻，有限状态控制器处 于某个状态，读/写头将扫描带上的 一个单元 依照状态和扫描到的带上符号， 图灵机将有一个动作如下：
有限状态控制器的状态进行改变； 把刚刚扫描过的单元上符号擦除掉， 并印刷上一个新的符号（有可能印刷上 与原来符号相同的符号）； 读/写头向左或者向右移动一个单元； 或者读/写头不移动。
start， accept，δ） Q={start ， del_b ， del_c ， seek_a ， check1，check2，check3，accept} ∑={a，b，c} ∑′={a，b，c，B，#，$，!}
指令
①读到一个a，用#代替它，向右寻找b <start, a , del_b , # , R> <del_b , a , del_b , a, R> <del_b ,# ,del_b, #, R> <del_b ,$, del_b ,$, R>
定义6-2 图灵机的格局ID
w1qw2∈ w1是读/写头左边带上的符号串 q是图灵机当前所处的状态 w2是读/写头右边的带上的符号串
(∑′)*Q(∑′)*
δ(q，x)
图灵机在格局w1qw2时停机
若w1qw2=w1qxw对于 ? 无定义。
定义6-3 格局的转换
若 M 在 w1qw2 上不停机，则如下定义