大学物理(4.2.2)--转动惯量转动定律
- 格式:pdf
- 大小:314.81 KB
- 文档页数:20



大学物理实验报告-刚体转动定律
实验目的:探究刚体转动的基本定律。
实验仪器:转动台、刚体转轴、刚体、刻度盘、秤、细线、阻尼器。
实验原理:刚体转动的基本定律包括:1)转动定律:刚体受
外力矩的作用产生角加速度,且角加速度与作用力矩成正比,与物体的转动惯量成反比;2)动量定理:刚体的角动量在无
外力矩作用下保持守恒。
实验步骤:
1. 将转动台放在水平桌面上,并调整水平度。
2. 将刚体转轴安装在转动台上,保证转轴能够自由转动。
3. 在转轴上放置刚体,并固定好。
4. 将刻度盘压在转轴上,确保盘面与刚体转动面平行,并零位对准。
5. 在刚体上绑上细线,另一端挂上适量的重物。
6. 调整阻尼器,使刚体转动不受外界干扰。
7. 按下计时器,同时放开刚体。
8. 记录刚体的转动时间,并测量刚体转过的角度。
9. 重复实验多次,取平均值。
实验数据处理:
1. 根据实验数据计算刚体的转动惯量,转动惯量的计算公式为:
I = m * g * R * T^2 / (2 * π^2 * θ),其中m为挂在细线末端的
重物质量,g为重力加速度,R为细线长度,T为转动时间,θ
为刚体转过的角度。
2. 将实验得到的转动惯量与刚体的几何结构进行比较,检验是
否符合刚体转动定律。
3. 计算实验误差,评估实验结果的可靠性。
实验注意事项:
1. 安全操作,避免伤害自己和他人。
2. 实验时要保持转动台的稳定,阻尼器的正确调整。
3. 实验时要注意量具的准确读数和记录。
4. 实验结束后,保持实验环境整洁,归还实验器材。
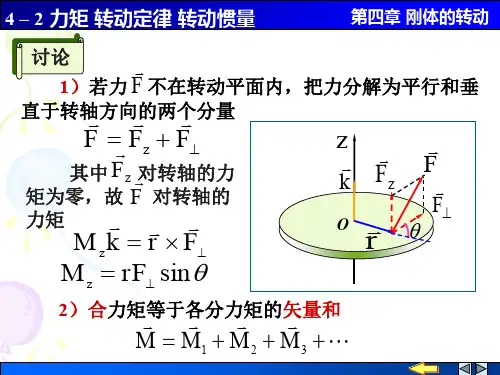
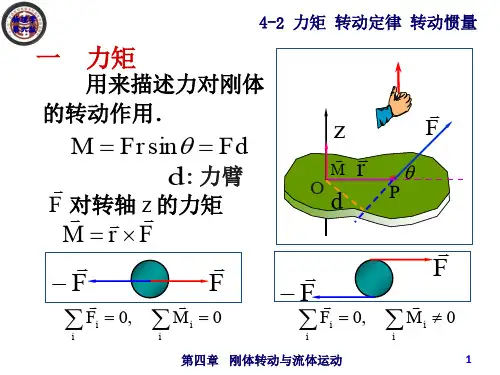


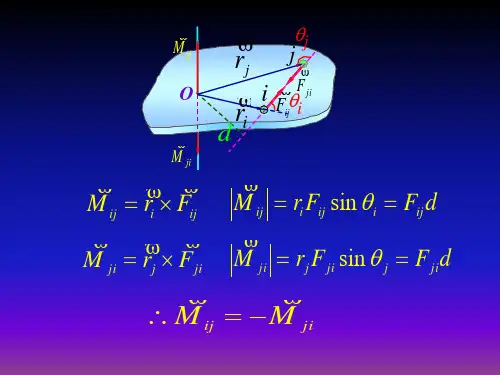
转动惯量的公式
转动惯量的公式是描述物体对转动运动的惯性大小的一个重要参数。
在物理学中,转动惯量通常用大写字母I表示,它与物体的质量分布以及物体对旋转轴的距离有关。
转动惯量的公式可以表示为I = Σmiri^2,其中Σ代表对所有质点求和,mi代表每个质点的质量,ri代表质点到旋转轴的距离。
转动惯量的公式对于描述物体在转动运动中的惯性特征非常重要。
通过计算转动惯量,我们可以了解物体对旋转的抵抗程度,即物体在转动过程中对外界施加的作用力所需的能量。
转动惯量的大小取决于物体的质量分布情况,质量分布越集中,转动惯量越小;质量分布越分散,转动惯量越大。
在实际应用中,转动惯量的公式可以帮助我们计算物体在转动运动中的角加速度、角速度以及角动量等物理量。
通过转动惯量的计算,我们可以更好地理解物体在转动运动中的行为规律,从而为工程设计和科学研究提供重要参考。
除了在理论物理中的应用,转动惯量的公式在工程领域也具有重要意义。
例如,在机械工程中,通过计算机械零件的转动惯量,可以帮助工程师设计出更加稳定和高效的机械系统。
在航天航空领域,转动惯量的计算也是设计飞行器和卫星轨道的重要依据之一。
总的来说,转动惯量的公式是描述物体对转动运动的惯性大小的重
要工具,它在物理学、工程学以及其他领域都具有广泛的应用价值。
通过深入理解转动惯量的公式,我们可以更好地认识物体在转动运动中的特性,为科学研究和工程实践提供有力支持。



第二讲
转动惯量 转动定律
O r
m z
※ 质点的转动惯量
F
θt
F n
F
αr m ma F ==t t M
(1)设单个质点
与转轴刚性连接
m α
2
mr M =α
θ2
t sin mr rF rF M ===第二讲 转动惯量 转动定律
定义: 为质点m 对O 点的 “转动惯量”2
mr
J =α
J M =2/20
α
2
i e j
j j j r m M M ∆=+ 质量元受外力 ,内力j F e j
F i 外力矩
内力矩
O
z
j
m ∆j
r j
F e j
F i α
2i e j
j j
j j
j
r m M M
∑∑∑∆=+0
=∴-=∑j
ij ji
ij M M M α
2
mr M =※ 刚体的转动惯
量
刚体定轴转动的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比.
)α
r m M
j
j j
j
2e (∑∑∆=※ 转动定律
α
J M =2
j
j
j r m J ∑∆=定义刚体转动惯量:O
z
j
m ∆j
r
j
F e j
F i ⎰=m
r J d 2
4/20
讨论
J
M ∝
α(2)t J
J M d d ω
α==(3)(1)
不变ωM ,0=*转动定律*
αJ M =t
v
m
ma F d d ==比较:
*转动惯量* 转动惯量的意义:转动惯性的量度 转动惯量的单位:kg·m 22j
j
j r
m J ∑∆=
⎰=m
r J d 2
转动惯量是对某一转轴的
转动惯量具有可叠加性
转动惯量与刚体的质量、质量的分布及转轴的位置
有关。
6/20
质量离散分布
222
221
12j
j j
j r
m r m r m r m J +++=∆=∑ J 的计算方法 质量连续分布
V
r m
r r m J V
j
j
j d d 2
2
2ρ⎰⎰∑==∆= :质量元m d :体积元
V d
例题 均匀杆m ,求对O 轴的转动惯量
C A
m
l 2
l
2
x d x
x
O
l
23
2
2
3
13ml
l dx x dm x J l
O ====⎰⎰λλ
2
3
2
/2
/2
212
1121ml l dx x dm x J l l C ===
=
⎰⎰-λλ
运用微积分思想和方法dx
dm l
m λλ==
8/20
例题 求半径为R 均匀圆
环m 对圆心C 的转动惯
量:
例题 求半径为R 均匀圆盘
m 对轴的转动惯量:24
2
2
2
122mR
R rdr
r dm r
J R
===
=
⎰⎰
σππσ∆m
i
∑∑∆=∆=i
i C m R R m J 22C R 2
mR
J C =½圆环?¼圆环?距轴R 的质点?
r
运用微积分思想和方法
2
r dm dJ =rdr
dm πσ2=2
R
m πσ=
2
md
J J C O +=※ 平行轴定理
质量为 的刚体,如果对
其质心轴的转动惯量为
,则对任一与该轴平行,相距为
的转轴的转动惯量为:
C J m d d
C O
m 10/20
平行轴定理的证明
2
md
J J C O +=∑∑+∆=∆=i
i
i
i
i i i C y x m r m J )
(222
∑∑'+'∆='∆=i
i
i i i i i O y x m r m J )
(2
2
2
i
i i i i i z z d y y x x ='-='=',
,
C 为刚体的质心,J C 为通过质心轴的转动惯量
∑∑-+∆='∆=i
i
i i
i i i O d y x m r m J ]
)([2
22
∑∑∑∆-∆++∆=i
i
i
i
i i i i i O y m d m d y x m J 2)(222∑=∆C
i
i
my y
m 质心通过坐标原点,y C =0
=m
=0
y
x z J J J += y
x
z 圆盘 R C m ※ 垂直轴定理
J
m r
m x m y z
i i
i i
i
i
==+∑∑∑∆∆∆2
22
薄板型物体
222
i
i
y
x r i +=12/20
竿子长些还是短些较安全
? 飞轮的质量为什么大都分布于外轮缘?
(2) 为瞬时关系
(3) 转动中 与平动中
地位相同.
ma F =αJ M =(1) 与 方向相同
M α说明
转动定律应用αJ M =14/20
例2质量为m
A
的物体A静止在光滑水平面上,和一质量不计的绳索相连接,绳索跨过一半径为R、
质量为m
C 的圆柱形滑轮C,并系在另一质量为 m
B
的物体B上,B竖直悬挂。
滑轮与绳索间无滑动, 且滑轮与轴承间的摩擦力可略去不计.(1)两物体的线加速度为多少? 水平和竖直两段绳索的张力各为多少?(2)物体 B从静止落下距离 y 时,其速率是多少?
解 (1) 用隔离法分别对各物体作受力分析,取如图所示坐标系。
A
B
C
A
m B m C
m A
P O x
T1
F N
F
A m y
O
T2
F ' B P B
m T2
F T1
F ' C
P C
F 16/20
a
m F A T1=a
m F g m B T2B =-αJ RF RF =-T1T2α
R a =y
O
T2F ' B P B m T2
F T1
F ' C
P C
F A
P O x
T1
F N
F A m 转动定律
牛顿定律
2
C B A B m m m g
m a ++=
2
C B A B A T1
m m m g
m m F ++=
2
)2(C B A B C A T2
m m m g m m m F +++=
解得:
B
A B A T2
T1m m g
m m F F +=
=如令 ,可得
0C =m 18/20
(2) B 由静止出发作匀加速直线运动,下落的速率 v
2
/22C B A B m m m gy
m ay ++=
=v ay v ady
vdv y
v
=⇒
=⎰⎰
2
2
1dy
dv v
dt dy dy dv dt dv a ===
同学们再见!。