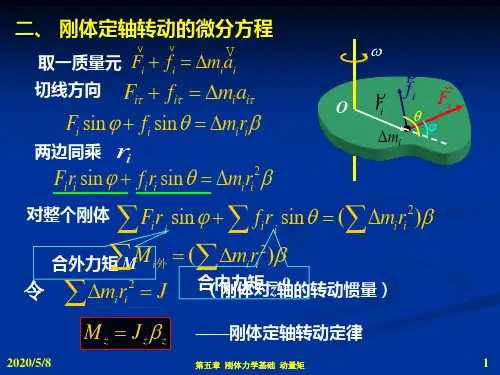
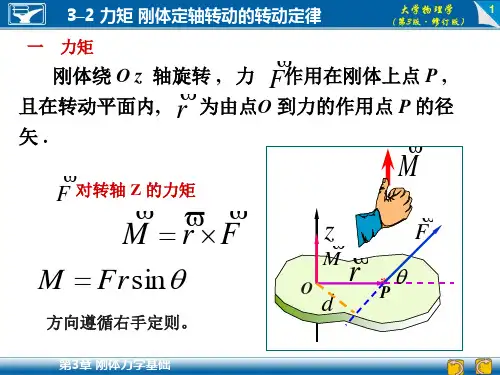
定轴转动定律 转动惯量
- 格式：ppt
- 大小：609.50 KB
- 文档页数：17
下载文档原格式
合集下载
一,刚体的定轴转动(运动)二,力矩,刚体定轴转动的转动定律,转动惯量
二、刚体定轴转动的转动定律
～利用力矩定义＋牛顿第二定律，研究刚体作定 轴转动的动力学规律。 设：oz为定轴， 为 P 刚体中任一质点 i ，其 质量为 ∆ m i。质点 iv ur 受外力 F i ，内力 F i ′ 的作用，均在与 O z 轴 相垂直的同一平面内。 ①牛顿第二定律： ur r v F i + Fi ′ = ∆ m i a i 建立自然坐标：切向、法向；
三、转动惯量 J 1.转动惯量的物理意义： 当以相同的力矩分别作用于两个绕定轴转动的不同 刚体时，它们所获得的角加速度一般是不一样的，转 动惯量大的刚体所获得的角加速度小，即角速度改变 得慢，也就是保持原有转动状态的惯性大；反之，转 动惯量小的刚体所获得的角加速度大，即角速度改变 得快，也就是保持原有转动状态的惯性小。因此，转 动惯量是描述刚体在转动中的惯性大小的物理量。 2.与转动惯量有关的因素：①刚体的质量；②转轴的 位置；③刚体的形状。 实质与转动惯量有关的只有前两个因素。形状即质量 分布，与转轴的位置结合决定转轴到每个质元的矢径。
R 3
例3、求长为L、质量为m的均匀细棒对图中不同轴的 转动惯量。 B 解：取如图坐标，dm=λdx A
J
A
=
∫
∫
L
0
x 2 λ dx = mL 2 / 3
A
x λ dx = mL
2 2
JC =
L 2 L − 2
L C L/2 L/2
X B X
/ 12
例4. 求质量 m ,半径 R 的球壳对直径的转动惯量 解：取离轴线距离相等的点的 集合为积分元
F i t ri + F i t′ ri = ∆ m i ri 2 α
外力矩 内力矩
③对所有质元的同样的式子求和：
定轴转动刚体的转动定律度力矩角动量转动惯量
Iz Ix Iy
z
定理证明：
对于质量平面分布的刚体， 绕 x 轴的转动惯量为：
o
yy
Ix y2dm
x
dm
绕 y 轴的转动惯量为：
I y x2dm
x
绕 z 轴的转动惯量为：
19
z
Iz z2dm (x 2 y2 )dm
y2dm x 2dm I x I y 证毕
o
yy
x z dm
0
M
绕圆环质心轴的转动惯量为
dm
oR
I MR2
例2：在无质轻杆的 b 处 3b 处各系质量为 2m 和 m 的 质点，可绕 o 轴转动，求：质点系的转动惯量I。
解：由转动惯量的定义
I
2
mi ri 2
2mb 2
m
(3b)2
11mb 2
i 1
9
例3： 如图所示，一质量为m、长为l的均质空心圆柱
体（即圆筒圆筒）其内、外半径分别为R1和R2。试求
的质元受阻力矩大，
细杆的质量密度 m
l
质元质量 dm dx
o
xl dm m dx
x
质元受阻力矩：
dM 阻 dmgx
细杆受的阻力矩
m l
M阻
dM
阻
0l
gxdx
1 2
gl 2
1 2
mgl
4
二、定轴转动刚体的角动量
1 .质点对点的角动量
L
r
P
r
mv
作圆周运动的质点的角动量L＝rmv;
l
x2dm
L
x2dx
1 L3
0
1 mL2
0
3
A
刚体定轴转动定律
角称为角坐标（或角位置）。 角坐标为标量。但可有正负。
o
P
x
2.角位移
描写刚体位置变化的物理量。
角坐标的增量：
称为刚体的角位移
y v2 p v1
P
3.角速度
R
x
描写刚体转动快慢和方向
的物理量。
角速度 lim d
t0 t dt 方向：满足右手定则，沿刚体转动方向右旋大拇指指向。
角速度是矢量，但对于刚体定轴 转动角速度的方向只有两个，在表 示角速度时只用角速度的正负数值 就可表示角速度的方向，不必用矢 量表示。
11mb 2
例4、半径为 R 质量为 M 的 圆环，绕垂直于圆环平面的 质心轴转动，求转动惯量J。
解： J R2dm MR 2
M o R dm
例5、半径为 R 质量为 M 的圆盘，绕垂直于圆盘 平面的质心轴转动，求转动惯量 J。
解：分割圆盘为圆环
dm
M
R2
2
rdr
J r2dm
M
dr
R
0
t 细杆绕一端的转动惯量
J 1 ml 2 3
摩擦阻力
t
例8、质量为 m1 和m2 两个物体， 跨在定滑轮上 m2 放在光滑的桌 面上，滑轮半径为 R，质量为 M，求：m1 下落的加速度，和 绳子的张力 T1、T2。
解：m1 g T1 m1a （1）
T2 m2a
b)作圆周运动的质点的角动量 L＝ r m v
c)角动量是描述转动状态的物理量；
P L
d)质点的角动量又称为动量矩。
or
dL
d (r mv)
dr
mv
r
d (mv)
r
F
dt
o
P
x
2.角位移
描写刚体位置变化的物理量。
角坐标的增量：
称为刚体的角位移
y v2 p v1
P
3.角速度
R
x
描写刚体转动快慢和方向
的物理量。
角速度 lim d
t0 t dt 方向：满足右手定则，沿刚体转动方向右旋大拇指指向。
角速度是矢量，但对于刚体定轴 转动角速度的方向只有两个，在表 示角速度时只用角速度的正负数值 就可表示角速度的方向，不必用矢 量表示。
11mb 2
例4、半径为 R 质量为 M 的 圆环，绕垂直于圆环平面的 质心轴转动，求转动惯量J。
解： J R2dm MR 2
M o R dm
例5、半径为 R 质量为 M 的圆盘，绕垂直于圆盘 平面的质心轴转动，求转动惯量 J。
解：分割圆盘为圆环
dm
M
R2
2
rdr
J r2dm
M
dr
R
0
t 细杆绕一端的转动惯量
J 1 ml 2 3
摩擦阻力
t
例8、质量为 m1 和m2 两个物体， 跨在定滑轮上 m2 放在光滑的桌 面上，滑轮半径为 R，质量为 M，求：m1 下落的加速度，和 绳子的张力 T1、T2。
解：m1 g T1 m1a （1）
T2 m2a
b)作圆周运动的质点的角动量 L＝ r m v
c)角动量是描述转动状态的物理量；
P L
d)质点的角动量又称为动量矩。
or
dL
d (r mv)
dr
mv
r
d (mv)
r
F
dt
力学10-转动定律,转动惯量,刚体绕定轴转动中的功、能量、功能关系
12
第五章 刚体力学基础 动量矩
§5-3 绕定轴转动刚体的动能 动能定理
一. 转动动能
设系统包括有 N 个质量元 取 ∆mi,其动能为 其动能为
ω
O
z
1 1 2 2 2 Eki = ∆mivi = ∆miri ω 2 2
刚体的总动能
r ri
r vi
P
• ∆mi
1 1 2 2 2 1 Ek = ∑Eki = ∑ ∆mi ri ω = ∑∆mi ri ω2 = Jω2 2 2 2
第五章 刚体力学基础 动量矩
m1g
m2g
五式联立，可解 五式联立，可解T1，T2，a1，a2，β
2012-4-16 11
总结
力的瞬时作用规律 力矩的瞬时作用规律
v F =0
v v F = ma
静止 匀速直线
M = Jβ
M = 0 静止 匀角速转动
J—转动时惯性大小的量度 转动时惯性大小的量度 力矩的持续作用规律： 力矩的持续作用规律： 空间： 空间： 时间： 时间：
(2) M、J、β必须对同一转轴定义。 必须对同一转轴定义。 、 、 必须对同一转轴定义 (3) M 正比于 β ，力矩越大，刚体的 β 越大 。 力矩相同，若转动惯量不同，产生的角加速度不同。 (4) 力矩相同，若转动惯量不同，产生的角加速度不同。
M (5) 与牛顿定律比较： → F, J → m, β → a 与牛顿定律比较：
14
讨论
(1) 力矩对刚体的功就是力对刚体的功。 力矩对刚体的功就是力对刚体的功。
θ2 θ2
1
(2) 合力矩的功
A= ∫
θ1
∑Midθ = ∑∫θ i i
Midθ = ∑Ai
第五章 刚体力学基础 动量矩
§5-3 绕定轴转动刚体的动能 动能定理
一. 转动动能
设系统包括有 N 个质量元 取 ∆mi,其动能为 其动能为
ω
O
z
1 1 2 2 2 Eki = ∆mivi = ∆miri ω 2 2
刚体的总动能
r ri
r vi
P
• ∆mi
1 1 2 2 2 1 Ek = ∑Eki = ∑ ∆mi ri ω = ∑∆mi ri ω2 = Jω2 2 2 2
第五章 刚体力学基础 动量矩
m1g
m2g
五式联立，可解 五式联立，可解T1，T2，a1，a2，β
2012-4-16 11
总结
力的瞬时作用规律 力矩的瞬时作用规律
v F =0
v v F = ma
静止 匀速直线
M = Jβ
M = 0 静止 匀角速转动
J—转动时惯性大小的量度 转动时惯性大小的量度 力矩的持续作用规律： 力矩的持续作用规律： 空间： 空间： 时间： 时间：
(2) M、J、β必须对同一转轴定义。 必须对同一转轴定义。 、 、 必须对同一转轴定义 (3) M 正比于 β ，力矩越大，刚体的 β 越大 。 力矩相同，若转动惯量不同，产生的角加速度不同。 (4) 力矩相同，若转动惯量不同，产生的角加速度不同。
M (5) 与牛顿定律比较： → F, J → m, β → a 与牛顿定律比较：
14
讨论
(1) 力矩对刚体的功就是力对刚体的功。 力矩对刚体的功就是力对刚体的功。
θ2 θ2
1
(2) 合力矩的功
A= ∫
θ1
∑Midθ = ∑∫θ i i
Midθ = ∑Ai
刚体定轴转动定律 转动惯量
动力学中，常选质心为基点。
5
三、力矩
用来反映力对刚体产生转
动效应的物理量．
M F r sin F d
d : 力臂
z
M
r
Od
其中： r 是力的作用点到轴的垂直距离。
F
P*
6
讨论
（1）若力矢量不在转 动平面内. F Fz F
其中 F z对转轴的力矩为零
M z rF sin
（2）合力矩等于各分力矩的矢量和 （3）刚体内力矩之和等于零
刚体力学
一、刚体（rigid body）的概念 二、刚体的运动形式 三、刚体的力矩 四、刚体定轴转动定律
1
一. 刚体（rigid body）的概念
受力的作用时，其大小和形状都不发生变化的物 体------刚体
说明：（1）刚体是理想模型。
（2）特殊的质点系，其上各质点间的距离保持不变 。
二 . 刚体的运动形式
▲ 定点转动： 运动中刚体上只有一点固定不动
整个刚体绕过该定点的某 一瞬时轴线转动。
4
3.一般运动： 刚体不受任何限制的任意运动。
它可分解为以下两种刚体的基本运动：
▲ 随基点O（可任选）的平动
▲ 绕通过基点O的瞬时轴的定点转动
例如：
· O 或
O
· · · O
O
两种分解，基点选取不同， 平动可以不同，转动却相同， 转动与基点的选取无关。
1.平动（translation）：连接刚体内任意两点的直 线在运动各个时刻的位置都彼此平行。
刚体做平动时，可用质心 或其上任何一点的运动来代 表整体的运动。
平动是刚体的基本运动形式之一。
3
2.转动（rotation）：
转动也是刚体的基本运动形式之一，它又可分为定轴转动和
5
三、力矩
用来反映力对刚体产生转
动效应的物理量．
M F r sin F d
d : 力臂
z
M
r
Od
其中： r 是力的作用点到轴的垂直距离。
F
P*
6
讨论
（1）若力矢量不在转 动平面内. F Fz F
其中 F z对转轴的力矩为零
M z rF sin
（2）合力矩等于各分力矩的矢量和 （3）刚体内力矩之和等于零
刚体力学
一、刚体（rigid body）的概念 二、刚体的运动形式 三、刚体的力矩 四、刚体定轴转动定律
1
一. 刚体（rigid body）的概念
受力的作用时，其大小和形状都不发生变化的物 体------刚体
说明：（1）刚体是理想模型。
（2）特殊的质点系，其上各质点间的距离保持不变 。
二 . 刚体的运动形式
▲ 定点转动： 运动中刚体上只有一点固定不动
整个刚体绕过该定点的某 一瞬时轴线转动。
4
3.一般运动： 刚体不受任何限制的任意运动。
它可分解为以下两种刚体的基本运动：
▲ 随基点O（可任选）的平动
▲ 绕通过基点O的瞬时轴的定点转动
例如：
· O 或
O
· · · O
O
两种分解，基点选取不同， 平动可以不同，转动却相同， 转动与基点的选取无关。
1.平动（translation）：连接刚体内任意两点的直 线在运动各个时刻的位置都彼此平行。
刚体做平动时，可用质心 或其上任何一点的运动来代 表整体的运动。
平动是刚体的基本运动形式之一。
3
2.转动（rotation）：
转动也是刚体的基本运动形式之一，它又可分为定轴转动和
刚体定轴转动的转动定律力矩
力矩平衡的条件
静平衡
刚体在转动过程中，如果合力矩 为零，则刚体保持静止状态。
动平衡
刚体在转动过程中，如果合力矩为 零，则刚体保持匀速转动状态。
平衡状态
无论是静平衡还是动平衡，刚体的 平衡状态都满足合力矩为零的条件。
力矩平衡的应用
机械平衡
在机械设计中，通过调整刚体的质量 分布或添加平衡装置，使刚体在转动 过程中满足力矩平衡条件，以保证机 械设备的稳定性和可靠性。
刚体的定轴转动
定轴转动：刚体绕某一固定轴线作旋 转运动。
在定轴转动中，刚体的角速度和角加 速度是矢量，其方向沿固定轴线，而 力矩是改变刚体转动状态的唯一物理 量。
刚体定轴转动的特点
角速度矢量、角加速度矢量和力 矩矢量都与固定轴线平行。
刚体定轴转动时，其上各点的速 度方向与该点到轴线的垂直线段 相垂直，各点的加速度方向与该
实例三：旋转木马的旋转
总结词
旋转木马的旋转是刚体定轴转动的又一实例，通过外力矩的作用，使旋转木马绕轴转动。
详细描述
旋转木马在外力矩的作用下开始转动，当旋转木马转动时，由于摩擦阻力和空气阻力的作用，旋转木 马会逐渐减速并最终停止。
实例四：陀螺的稳定旋转
总结词
陀螺的稳定旋转是刚体定轴转动的最后一个实例，陀螺通过自转保持稳定的旋转状态。
在日常生活和工业生产中，转动 定律也广泛应用于各种旋转运动
的分析和设计。
04
刚体定轴转动的力矩平衡
力矩平衡的概念
力矩平衡
刚体在转动过程中，受到 的力矩之和为零，即合力 矩为零。
力矩
力对转动轴的力矩等于力 和力臂的乘积，其中力臂 是从转动轴到力的垂直距 离。
转动轴
刚体转动的中心轴，可以 是固定的点或线。
力矩 刚体定轴转动的转动定律
dJ R dm
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
12
考虑到所有质元到转轴的距离均为R，所以细圆环对 中心轴的转动惯量为
J dJ R dm R
2 m
2
m
dm mR
2
(2)求质量为m，半径为R的圆盘对中心轴的转动惯量
m 如图 dS 2 rdr , , dm dS 2 rdr 2 R
l 2
o
P
d d d d dt d dt d
代入初始条件积分 得
第3章 刚体力学基础
3g d sin d 2l 3g (1 cos ) l
1 2 J x dx ml 0 3
l 2
由此看出，同一均匀细棒，转轴位置不同，转动惯 量不同.
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
11
例3.2 设质量为m，半径为R的细圆环和均匀圆盘分 别绕通过各自中心并与圆面垂直的轴转动，求圆环和 圆盘的转动惯量. 解 (1) 在环上任 取一质元，其质量 为dm，距离为R， 则该质元对转轴的 转动惯量为
解 (1)转轴通过棒的中心并与棒垂直
m l
dm dx
dJ x 2dm x 2dx
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
10
整个棒对中心轴的转动惯量为
J dJ
l 2 l 2
1 x dx ml 2 12
2
(2)转轴通过棒一端并与棒垂直时，整个棒对该轴的 转动惯量为
解 (1) M k 2 ，故由转动定律有
k k J 即 J 2 1 k0 0 3 9J
10 刚体定轴转动 力矩 转动定律 转动惯量
若棒的质量均匀分布: M 1 mgl sin
2 解：
dMdm gxsin
O
x
2 x d x g x sin 2 g sin x 2 d x
ml
dmg
M 0 l2gsinx2dx2 3gl3sin
例 有一大型水坝高110 m、长1 000 m ,
水深100m，水面与大坝表面垂直，如图所 示. 求作用在大坝上的力，以及这个力对通
i Fji
Fij
M ji
MijMji
一 力矩
用来描述力对刚体
的转动作用．
M Fsrin Fd
d: 力臂
FM 对 转r轴F z的力矩
z
F
O
M r
d
P*
M 方向: 沿转轴，与刚体转动方向 构成右手螺旋关系的方向．
M 方向: 沿转轴， 与刚体转动方向构 成右手螺旋关系的 方向．
其中 Fz对转轴的
力矩为零，故 F对转 轴的力矩
M zrF rF
z
F
k
O
r Fz
F
M zrF sink
（2）合 力矩 等于 各分力矩的矢量和 M M 1 M 2 M 3
M r F r F 1 F 2 . .F n . r F 1 r F 2 . .r . F n
：质量面密度
对质量体分布的刚体：dmdV
：质量体密度
例 一质量为 m、长为 l 的均匀细长棒，求
通过棒中心并与棒垂直的轴的转动惯量 .
Or
Or
l 2 O´ dr l 2
O´ dr l
转动定律、转动惯量讲解
Fit*ri+Fit'*ri= Δmi*(ri^2)*α
这是一个质点的规律，如果把所有的质点加起来，即∑Fit*ri+∑Fit'*ri= ∑Δmi*(ri^2)*α，因为刚体内部质点间的合力对转轴的力矩为零，即∑Fit'*ri= 0， 于是就有∑Fit*ri = ∑Δmi*(ri^2)*α，等式左边表示刚体所有质点所受外力对转轴 的力矩，也就是合力矩M；
《地球能平稳转动而不受外界干扰，全 靠转动定律与转动惯量》
上一章讲了刚体的定轴转动与角速度和角加速度的概念，如果有外力作用在刚体 上，那么刚体会发生什么变化呢？这就是本章要讲到的力矩、转动定律以及转动 惯量等概念。
首先来说力矩，在如图1所示的坐标系中，有一外力F作用在刚体内的P点，刚体 相对于原点的位置矢量为r，显然力F不经过原点O，于是把从O点到力F延长线的 垂直距离d叫做力F对转轴的力臂，其大小d=rsinθ ，而力F的大小和力臂d的乘积 Frsinθ 就叫做F对转轴的力矩，用大写字母M表示，力矩除了有小外，也有方向，
为了深刻理解转动惯量，以地球的转动惯量公式Je = (2mR^2)/5为例子，将地 球质量和半径带入式子可知，地球在转动时转动惯量非常大，根据转动定律可知， 需要非常大的力矩才能使地球加速或者减速，对于地球表面的所有物体而言，没 有哪个物体可以提供这样的力矩，这也就是地球平稳转动的原因。
讲完了转动定律，下一章《芭蕾舞演员的旋转加速秘诀-角动量守恒》将继续讲 解角动量。
而等式右边表示的量只与刚体的形状、质量、刚体的转轴有关。这个量就叫做转 动惯量，用大写字母J表示。于是等式可以表示为：M=J *α。这就是刚体的转动 定律，它的形式对应牛顿第二定律，其物理意义就是在同一力矩下，转动惯量大 的刚体，获得的角加速度就小，转动惯量小的刚体获得的角加速度就大。
这是一个质点的规律，如果把所有的质点加起来，即∑Fit*ri+∑Fit'*ri= ∑Δmi*(ri^2)*α，因为刚体内部质点间的合力对转轴的力矩为零，即∑Fit'*ri= 0， 于是就有∑Fit*ri = ∑Δmi*(ri^2)*α，等式左边表示刚体所有质点所受外力对转轴 的力矩，也就是合力矩M；
《地球能平稳转动而不受外界干扰，全 靠转动定律与转动惯量》
上一章讲了刚体的定轴转动与角速度和角加速度的概念，如果有外力作用在刚体 上，那么刚体会发生什么变化呢？这就是本章要讲到的力矩、转动定律以及转动 惯量等概念。
首先来说力矩，在如图1所示的坐标系中，有一外力F作用在刚体内的P点，刚体 相对于原点的位置矢量为r，显然力F不经过原点O，于是把从O点到力F延长线的 垂直距离d叫做力F对转轴的力臂，其大小d=rsinθ ，而力F的大小和力臂d的乘积 Frsinθ 就叫做F对转轴的力矩，用大写字母M表示，力矩除了有小外，也有方向，
为了深刻理解转动惯量，以地球的转动惯量公式Je = (2mR^2)/5为例子，将地 球质量和半径带入式子可知，地球在转动时转动惯量非常大，根据转动定律可知， 需要非常大的力矩才能使地球加速或者减速，对于地球表面的所有物体而言，没 有哪个物体可以提供这样的力矩，这也就是地球平稳转动的原因。
讲完了转动定律，下一章《芭蕾舞演员的旋转加速秘诀-角动量守恒》将继续讲 解角动量。
而等式右边表示的量只与刚体的形状、质量、刚体的转轴有关。这个量就叫做转 动惯量，用大写字母J表示。于是等式可以表示为：M=J *α。这就是刚体的转动 定律，它的形式对应牛顿第二定律，其物理意义就是在同一力矩下，转动惯量大 的刚体，获得的角加速度就小，转动惯量小的刚体获得的角加速度就大。
008-刚体定轴转动定律、转动惯量
008-刚体定轴转动定律、转动惯量1. 选择题1. 两个匀质圆盘A 和B 的半径分别为A R 和B R ，若B A R R >，但两圆盘的质量相同，如两盘对通过盘心垂直于盘面轴的转动惯量各为J A 和J B ，则［ ］(A) J A ＞J B ． (B) J A ＜J B ． (C) J A ＝J B ． (D) 不能确定J A 、J B 哪个大． 答案：（A ）2. 两个匀质圆盘A 和B 的密度分别为A ρ和B ρ，若ρA ＞ρB ，但两圆盘的质量与厚度相同，如两盘对通过盘心垂直于盘面轴的转动惯量各为J A 和J B ，则［ ］(A) J A ＞J B ． (B) J A ＜J B ． (C) J A ＝J B ． (D) 不能确定J A 、J B 哪个大． 答案：（B ）3. 有两个半径相同，质量相等的细圆环A 和B ．A 环的质量分布均匀，B 环的质量分布不均匀．它们对通过环心并与环面垂直的轴的转动惯量分别为J A 和J B ，则［ ］(A) J A ＞J B ． (B) J A ＜J B ． (C) J A = J B ． (D) 不能确定J A 、J B 哪个大． 答案：（C ）4. 有两个半径相同的细圆环A 和B ．A 环的质量为A m ，B 环的质量B m ，而B A m m <。
它们对通过环心并与环面垂直的轴的转动惯量分别为J A 和J B ，则［ ］(A) J A ＞J B ． (B) J A ＜J B ． (C) J A = J B ． (D) 不能确定J A 、J B 哪个大． 答案：（B ）5. 质量相同的两根匀质棒，长度分别为A l 和B l ，B A l l <，两根棒对棒的中心的转动惯量分别为A J 和B J ，则［ ］(A) J A ＞J B ． (B) J A ＜J B ． (C) J A = J B ． (D) 不能确定J A 、J B 哪个大． 答案：（B ）6. 一刚体以每分钟60转绕z 轴做匀速转动(ω沿z 轴正方向)．设某时刻刚体上一点P 的位置矢量为k j i r 5 4 3++=，其单位为“10-2 m ”，若以“10-2 m ·s -1”为速度单位，则该时刻P 点的速度为：［ ］(A) k j i157.0 125.6 94.2++=v (B) j i 8.18 1.25+-=v(C) j i8.18 1.25--=v (D) k 4.31=v答案：（B ）7. 几个力同时作用在一个具有光滑固定转轴的刚体上，如果这几个力的矢量和为零，则此刚体［ ］ (A)必然不会转动． (B)转速必然不变． (C)转速必然改变． (D)转速可能不变，也可能改变． 答案：（D ）8. 一圆盘绕过盘心且与盘面垂直的光滑固定轴O 以角速度ω按图示方向转动.若如图所示的情况那样，将两个大小相等方向相反但不在同一条直线的力F 沿盘面同时作用到圆盘上，则圆盘的角速度ω［ ］(A) 必然增大． (B) 必然减少．(C) 不会改变 (D) 如何变化，不能确定.不能确答案：（A ）9. 关于刚体对轴的转动惯量，下列说法中正确的是［ ］ （A ）只取决于刚体的质量,与质量的空间分布和轴的位置无关． （B ）取决于刚体的质量和质量的空间分布，与轴的位置无关． （C ）取决于刚体的质量、质量的空间分布和轴的位置． （D ）只取决于转轴的位置，与刚体的质量和质量的空间分布无关． 答案：（C ）10. 均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图所示．今使棒从水平位置由静止开始自由下落，在棒摆动到竖直位置的过程中，下述说法哪一种是正确的？［ ］(A) 角速度从小到大，角加速度从大到小．(B) 角速度从小到大，角加速度从小到大．(C) 角速度从大到小，角加速度从大到小． (D) 角速度从大到小，角加速度从小到大． 答案：（A）11. 质量为m ，长为l 均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图所示．今使棒由静止开始从水平位置自由下落摆动到竖直位置。
第03章 刚体定轴转动01-转动定律
作用于刚体内每一质元上的内力矩的矢量和为零，即
fr 0
i i i
14
F r
i i
i
为作用于刚体内每一质元上的外力矩的矢量和。
M Fi ri
i
定义：刚体的转动惯量J (moment of interia) 则有：
2 m r ii i
M J
即：
M J
刚体定轴转动的转动定律：刚体定轴转动的角加速度与它所 受的合外力矩成正比 ，与刚体的转动惯量成反比。 —— 刚体定轴转动的基本动力学规律。
dm 2 π r dr
P
3 2
圆环对轴的转动惯量
dJ r dm 2π r dr R 3 J 2π r dr π R 4 0 2 1 2 而 m π R 所以 J mR 2
圆盘对P 轴的转动惯量
R
R
O O
r dr
1 J P mR 2 mR 2 2
19
15
三、转动惯量
J mi ri
i
2
物理意义：刚体转动惯性的量度。 对于质量离散分布刚体的转动惯量
J mi ri 2 m1r12 m2r22
i
质量连续分布刚体的转动惯量
J lim
mi 0
2 2 m r r i i dm i
P1 y
P2
23
（3）如图所示,不计绳子的质量，滑轮的质量与半径分别为M
和R，滑轮与绳间只滚不滑，不计滑轮与轴间的摩擦力。 且 m1 m2 。 求重物释放后，物体的加速度和绳的张力。 A
m1 FN m1 FT1
O
C
取坐标如图
M
刚体绕定轴转动的转动定律和转动惯量
0 R2
1 mR2 2
Z
m R2
R1
薄圆环
dm
ds
m (R22
R12
)
ds
ds 2 rdr
dJ r2dm
J R2 r 2
m
2 rdr
R1
(R22 R12 )
1 2
m(R22
R12 )
R
m
H
空心圆柱面
dm ds m ds 2 RH
ds 2 Rdh
dJ r2dm
J H R2 m 2 Rdh
0 2 RH
mR3
r
R
H m
实心圆柱
dm
dV
m
R2H
dV
dV 2 rHdr
dJ r2dm
J R r2 m 2 rHdr
0 R2H
R2 R1
H m
同轴空心圆柱
dm
dV
mg
H (R22
R12 )
dV
dV 2 rHdr
dJ r2dm
J R2 r2
mg
2 rHdr
R1 H (R22 R12 )
R
+
T1
+
T2
N
m
4m
2m ＋ o
P1
P2
mg
4m
T1
T2
2m
分别对人、物、滑轮建立方程：
4mg-T1 4ma人地
（1 ）
T2-2mg 2ma物地 2ma绳地 （2） R
T1R -T2 R
J
1 2
mR2
（3） m
人相对 绳匀加 速a0上爬，则
a人地 a人绳 a绳地
4m
刚体定轴转动定律
于 180°的夹角 θ 转向 F 时，拇指所指的方向就是力矩的方向。
可见，力矩的方向与转轴的方向平行，只有两个可能的方向，因此，可用 M 的正负表示力矩的方向。 一般可按力矩的作用来判断其正负：由转轴 Oz 正向俯视，若力矩的作用使刚体逆时针转动，则力矩为 正，否则为负。
刚体定轴转动定律 1.1 力矩
可加性
• 对同一转轴而言，刚体各部分转动惯量之 和等于整个刚体的转动惯量。
平行轴定理
• 设有两个彼此平行的转轴，一个通过刚体 的质心，另一个不通过质心。两平行轴之 间的距离为d，刚体的质量为m。
如果此刚体对通过质心转轴的转动惯量为 Jc ，则对另一 转轴的转动惯量 J 为 J Jc md 2
刚体定轴转动定律
刚体定轴转动定律Βιβλιοθήκη ， ，，，
例题讲解 2
如图所示，一轻绳跨过一轴承光滑的定滑轮。绳两边分别悬有质量为 m1 和 m2 的两个物体 A，B。已知 m1
小于 m2 ，滑轮可看作质量均匀分布的等厚圆盘，其质量为 m，半径为 r，设绳与滑轮间无相对滑动。求：① 物
体的加速度；② 滑轮的角加速度；③ 绳的张力。
i 1
n
用 M 表示，即 M (Δmiri2 ) β
i 1
n
n
式中的 (Δmiri2 ) 称为转动惯量，用 J 表示，即 J (Δmiri2 )
i 1
i 1
于是，式可写为 M Jβ
刚体定轴转动定律 1.2 转动定律
转动定律：刚体定轴转动时，刚体的角加速度与刚体所受的合外力矩成正比，与刚体的转动惯量 成反比。
r 2 dm
Ω
式中 r ——质元 dm 到转轴的距离（m）。 在国际单位制中，转动惯量的单位为 kg m2 。
可见，力矩的方向与转轴的方向平行，只有两个可能的方向，因此，可用 M 的正负表示力矩的方向。 一般可按力矩的作用来判断其正负：由转轴 Oz 正向俯视，若力矩的作用使刚体逆时针转动，则力矩为 正，否则为负。
刚体定轴转动定律 1.1 力矩
可加性
• 对同一转轴而言，刚体各部分转动惯量之 和等于整个刚体的转动惯量。
平行轴定理
• 设有两个彼此平行的转轴，一个通过刚体 的质心，另一个不通过质心。两平行轴之 间的距离为d，刚体的质量为m。
如果此刚体对通过质心转轴的转动惯量为 Jc ，则对另一 转轴的转动惯量 J 为 J Jc md 2
刚体定轴转动定律
刚体定轴转动定律Βιβλιοθήκη ， ，，，
例题讲解 2
如图所示，一轻绳跨过一轴承光滑的定滑轮。绳两边分别悬有质量为 m1 和 m2 的两个物体 A，B。已知 m1
小于 m2 ，滑轮可看作质量均匀分布的等厚圆盘，其质量为 m，半径为 r，设绳与滑轮间无相对滑动。求：① 物
体的加速度；② 滑轮的角加速度；③ 绳的张力。
i 1
n
用 M 表示，即 M (Δmiri2 ) β
i 1
n
n
式中的 (Δmiri2 ) 称为转动惯量，用 J 表示，即 J (Δmiri2 )
i 1
i 1
于是，式可写为 M Jβ
刚体定轴转动定律 1.2 转动定律
转动定律：刚体定轴转动时，刚体的角加速度与刚体所受的合外力矩成正比，与刚体的转动惯量 成反比。
r 2 dm
Ω
式中 r ——质元 dm 到转轴的距离（m）。 在国际单位制中，转动惯量的单位为 kg m2 。
刚体运动学转动惯量定轴转动
刚体运动学转动惯量定轴转动
（4）刚体运动学、转动惯量、定轴转动
一、刚体、刚体的运动 刚体：在外力作用下，形状和大小都不发生变化的物 体 . （任意两质点间距离保持不变的特殊质点组） 刚体的运动形式：平动(Translation )、转动( rotation)
➢ 平动：若刚体中所有点的运 动轨迹都保持完全相同，或者说 刚体内任意两点间的连线总是平 行于它们的初始位置间的连线
dm
面密 ,度 面： 元 dS ：
dV 体密 ,度 体： 元 dV ： dm
注意
刚体对轴的转动惯量 J
与刚体总质量有关 与刚体质量分布有关 与转轴的位置有关
只有对于几何形状规则、质量连续且均匀分布 的刚体，才能用积分计算出刚体的转动惯量
（4）刚体运动学、转动惯量、定轴转动
几 种 常 见 刚 体 的 转 动 惯 量
解：取半径为r宽为dr的薄圆环柱为微元
dmdV2rdrl
OR
d Ir2dm 2lr3dr
Id I0 R2 lr 3d r1 2R 4l转动惯量与l无关，
R m 2lI1 2m2 R
实心圆柱对其轴的转 动惯量也是mR2/2
（4）刚体运动学、转动惯量、定轴转动 练习
1.由长 l 的轻杆连接的质点如图所示，求质点系对过 A 垂直于纸面的轴的转动惯量
ct，即
d
ct ，积分
dc
t
tdt
得
dt 1 ct 2
0
0
2
当t=300s 时
18r0 m 0 1 i6 0 nπ 0 r0 a s 1 d
所以
c2 t22 3 62 0 π 0r0 0 a s d 37 πr5a s d 3
（4）刚体运动学、转动惯量、定轴转动
（4）刚体运动学、转动惯量、定轴转动
一、刚体、刚体的运动 刚体：在外力作用下，形状和大小都不发生变化的物 体 . （任意两质点间距离保持不变的特殊质点组） 刚体的运动形式：平动(Translation )、转动( rotation)
➢ 平动：若刚体中所有点的运 动轨迹都保持完全相同，或者说 刚体内任意两点间的连线总是平 行于它们的初始位置间的连线
dm
面密 ,度 面： 元 dS ：
dV 体密 ,度 体： 元 dV ： dm
注意
刚体对轴的转动惯量 J
与刚体总质量有关 与刚体质量分布有关 与转轴的位置有关
只有对于几何形状规则、质量连续且均匀分布 的刚体，才能用积分计算出刚体的转动惯量
（4）刚体运动学、转动惯量、定轴转动
几 种 常 见 刚 体 的 转 动 惯 量
解：取半径为r宽为dr的薄圆环柱为微元
dmdV2rdrl
OR
d Ir2dm 2lr3dr
Id I0 R2 lr 3d r1 2R 4l转动惯量与l无关，
R m 2lI1 2m2 R
实心圆柱对其轴的转 动惯量也是mR2/2
（4）刚体运动学、转动惯量、定轴转动 练习
1.由长 l 的轻杆连接的质点如图所示，求质点系对过 A 垂直于纸面的轴的转动惯量
ct，即
d
ct ，积分
dc
t
tdt
得
dt 1 ct 2
0
0
2
当t=300s 时
18r0 m 0 1 i6 0 nπ 0 r0 a s 1 d
所以
c2 t22 3 62 0 π 0r0 0 a s d 37 πr5a s d 3
（4）刚体运动学、转动惯量、定轴转动
转动惯量的测定原理
转动惯量的测定【实验目的】（1）学习用恒力矩转动法测定刚体转动惯量的原理和方法。
（2）观测刚体的转动惯量随其质量、质量分布及转轴不同而改变的情况，验证平行轴定理。
（3）学会使用通用电脑计时器来测量时间。
【实验原理】1. 恒力矩转动法测定转动惯量的原理根据刚体的定轴转动定律有M ＝J β （3.3.1）只要测定刚体转动时所受的总合外力矩M 及该力矩作用下刚体转动的角加速度β，则可计算出该刚体的转动惯量J 。
假设以某初始角速度转动的空实验台转动惯量为J 1，未加砝码时，在摩擦阻力矩M 的作用下，实验台将以角加速度β1作匀减速运动，即：－M μ＝J 1β1 （3.3.2）将质量为m 的砝码用细线绕在半径为R 的实验台塔轮上，并让砝码下落，系统在恒外力作用下将作匀加速运动。
若砝码的加速度为a ，则细线所受张力为()T m g a =-。
若此时实验台的角加速度为β2，则有a ＝R β2，细线施加给实验台的力矩为2()TR m g R R β=-，此时有：2μ12()m g R R M J ββ--= （3.3.3）将式（3.3.2）、（3.3.3）两式联立消去M μ后，可得：2121()mR g R J βββ-=- （3.3.4） 同理，若在实验台上加上被测物件后系统的转动惯量为J 2，加砝码前后的角加速度分别为β3与β4，则有4243()mR g R J βββ-=- （3.3.5） 由转动惯量的叠加原理可知，被测试件的转动惯量J 3为：321J J J =- （3.3.6）测得R 及β1、β2、β3、β4，由式（3.3.4），（3.3.5），（3.3.6）即可计算被测试件的转动惯量。
2. 刚体转动角加速度β的测量实验中采用XD-GLY 通用电脑计时器，记录下遮挡次数和相应的时间。
固定在载物台圆周边缘的两遮光片，每转动半圈遮挡一次固定在底座上的光电门，即产生一个计数光电脉冲。
计数器记录下遮挡次数和从第一次遮挡光到其后各次扫光所经历的时间，即是第二次扫光时，计时器计下的时间t 1是从第一次挡光开始载物台转动了π弧度所经历的时间；即第三次扫光时，计时器计下的时间t 2是从第一次挡光开始载物台转动了2π弧度所经历的时间…；第k+1次扫光，计时器计下的时间t k 是从第一次挡光开始载物台转动了k π弧度所经历的时间。
大学物理-力矩-转动定律-转动惯量
F
p
18
2 – 5 刚体的定轴转动
第二章 动力学基础
解 (1) Fr J
Fr 98 0.2 39.2 rad/s2
J 0.5
mg T ma
(2) Tr J
a r
两者区别?
rO
F T
T
J
mgr mr 2
98 0.2 0.5 10 0.22
i
J r2dm
9
2 – 5 刚体的定轴转动
第二章 动力学基础
四. J 的计算
质量连续分布刚体的转动惯量
J mjrj2 r2dm dm ：质量元 j
对质量线分布的刚体： dm dl
：质量线密度
对质量面分布的刚体：
：质量面密度
对质量体分布的刚体：
在圆规迹切线方向
mk ak mk rk Fk fk
两边乘以rk，并对整个刚体求和
第二章 动力学基础
z
o
vk
mk
( mk rk2 ) Fk rk fk rk
k
k
k
5
2 – 5 刚体的定轴转动
第二章 动力学基础
( mk rk2 ) Fk rk fk rk
17
2 – 5 刚体的定轴转动
第二章 动力学基础
四、转动定律的应用举例
例1 一轻绳绕在半径 r =20 cm 的飞轮边缘， 在绳端施以F=98 N 的拉力，飞轮的转动惯量 J=0.5 kg·m2,飞轮与转轴间的摩擦不计 。
rO
求: (1) 飞轮的角加速度。
(2) 如以重量P =98 N的物体挂在 绳端,试计算飞轮的角加速度。
定轴转动定律转动惯量
轮不打滑： 联立方程，可解得 FT1 ，FT2，a，β 。 ➢ 此装置称阿特伍德机——可用于测量重力加速度 g
例4-6 一半径为R，质量为m均质圆盘，平放在粗糙的
水平桌面上。设盘与桌面间摩擦因数为，令圆盘最 初以角速度0 绕通过中心且垂直盘面的轴旋转，问它
经过多少时间才停止转动？
解： 把 圆 盘 分 成 许 多 环 形
竿
子
长
些
还
是
短
些
较
安
飞轮的质量为什么
全 ？
大都分布于外轮缘？
例4-3 求均质细棒( m ，l ) 的转动惯量： (1) 转轴通过中心C与棒垂直， (2) 转轴通过棒的一端O与棒垂直。
解：(1) dm
C dx
x
dm (2)
O
dx
x
➢ 可见，转动惯量因转轴位置不同而变，故必须指 明是关于某轴的转动惯量。
质元，每个质元的质量
dm=reddr，e是盘的厚
度，质元所受到的阻力矩
d r R
dr
e
为 rdmg 。
圆盘所受阻力矩为
Mr rμdmg μg rρredθdr
Mr rμdmg μg rρredθdr
μgρe
2π
dθ
R r 2dr 2 μgρeπR3
0
0
3
m=eR2
Mr
2 3
μmgR
用线的距离，称为力臂。
3、在转轴方向确定后，力对转 轴的力矩方向可用正负号表示。
刚体所受的关于定轴的合力矩：
二、定轴转动定律
对刚体中任一质量元
mi
受外力 Fi 和内力 F内i
应用牛顿第二定律，可得
Fi F内i Δmiai
例4-6 一半径为R，质量为m均质圆盘，平放在粗糙的
水平桌面上。设盘与桌面间摩擦因数为，令圆盘最 初以角速度0 绕通过中心且垂直盘面的轴旋转，问它
经过多少时间才停止转动？
解： 把 圆 盘 分 成 许 多 环 形
竿
子
长
些
还
是
短
些
较
安
飞轮的质量为什么
全 ？
大都分布于外轮缘？
例4-3 求均质细棒( m ，l ) 的转动惯量： (1) 转轴通过中心C与棒垂直， (2) 转轴通过棒的一端O与棒垂直。
解：(1) dm
C dx
x
dm (2)
O
dx
x
➢ 可见，转动惯量因转轴位置不同而变，故必须指 明是关于某轴的转动惯量。
质元，每个质元的质量
dm=reddr，e是盘的厚
度，质元所受到的阻力矩
d r R
dr
e
为 rdmg 。
圆盘所受阻力矩为
Mr rμdmg μg rρredθdr
Mr rμdmg μg rρredθdr
μgρe
2π
dθ
R r 2dr 2 μgρeπR3
0
0
3
m=eR2
Mr
2 3
μmgR
用线的距离，称为力臂。
3、在转轴方向确定后，力对转 轴的力矩方向可用正负号表示。
刚体所受的关于定轴的合力矩：
二、定轴转动定律
对刚体中任一质量元
mi
受外力 Fi 和内力 F内i
应用牛顿第二定律，可得
Fi F内i Δmiai
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
d
r dr R e
M r rμdmg μg rρredθdr
M r rμdmg μg rρredθdr
2 3 μgρe dθ r dr μgρeπR 0 0 3 2 2 M r μmgR m=eR 3 2 1 2 d 由定轴转动定律： mgR I mR
2π R 2
3 2 t 0 2 1 μg dt R dω 0 3 2 ω0
dt
3 R t 0 4 g
作业：4.11、4.13、4.14
例4-3 求均质细棒( m ，l ) 的转动惯量： (1) 转轴通过中心C与棒垂直， (2) 转轴通过棒的一端O与棒垂直。 解：(1)
dm
C dx x
(2) O
dm
dx
x
可见，转动惯量因转轴位置不同而变，故必须指 明是关于某轴的转动惯量。
平行轴定理（parallel axis theorem）
刚体对任一转轴的转动惯量 I 等于对通过质心 的平行转轴的转动惯量 IC 加上刚体质量 m 乘以两平 行转轴间距离 d 的平方。
i i i
对于成对的内力，对同一转轴的力矩之和为零，则
F
i
内i
ri sin θi 0
2 i i i
F r sin (m r
i i i i
)
称为刚体对转轴的转动惯量。
d M z I I dt
刚体定轴转动定律：刚体在做定轴转动时，刚体的角 加速度与它所受到的合外力矩成正比，与刚体的转动 惯量成反比。 与平动定律比较：
d r sin 是转轴到力作
用线的距离，称为力臂。 3、在转轴方向确定后，力对转 轴的力矩方向可用正负号表示。 刚体所受的关于定轴的合力矩：
二、定轴转动定律
对刚体中任一质量元 mi
受外力 Fi 和内力 F i 内
Fi F内i Δmi ai
应用牛顿第二定律，可得
dv F ma m dt
三、转动惯量
定义： 单位( SI )：
刚体为质量连续体时：
（ r 为质元dm到转轴的距离） 转动惯量是刚体转动惯性大小的量度。转动惯量 取决于刚体本身的性质，即刚体的形状、大小、质 量分布以及转轴的位置。
飞轮的质量为什么 大都分布于外轮缘？
竿 子 长 些 还 是 短 些 较 安 全 ？
通过任一转轴A的转动惯量： （取C为坐标原点）
d A C
dm
dx x
mxC 0
正交轴定理
薄板状刚体对板面内相互垂直的两个定轴 X、Y 的 转动惯量之和，等于该刚体对通过两轴交点且垂直于 板面的定轴 Z 的转动惯量，即：
I Z I X IY
例4-4 求质量 m 半径 R 的 (1) 均质圆环， (2) 均质圆盘 对通过直径的转轴的转动惯量。
解：
(1) 圆环：
dm
(2) 圆盘：
O r
dm
可见，转动惯量与刚体的质量分布有关。
刚体的回转半径
rG ：
2 2
I mi ri mrG
i
rG
I m
例4-5 物体：m1、m2(>m1)， 定滑轮：m、r，受摩擦 阻力矩为Mr。轻绳不能伸长，无相对滑动。求物体的 加速度和绳的张力。 解：由于考虑滑轮的质量和所受 的摩擦阻力矩，
§4-2 定轴转动定律 转动惯量
一、力矩
F 对O点的力矩：
M
M r F
F
r
大小： 说明
M rF sin
1、只有垂直转轴的外力分量才产生 沿转轴方向的力矩Mz ，而平行于转 轴的外力分量产生的力矩 Mxy 则被 轴承上支承力的力矩所抵消。
2、 M z
rF2 sin φ F2 d
采用自然坐标系，上式切向分量式为
Fi sin i F内i sini mi ait mi ri
Fi ri sin i F内i ri sini mi ri 2
对刚体内各个质点的相应式子，相加得
Fi ri sin i F内i ri sini (mi ri 2 )
r
问题中包括平动和转动。
FT1 m1 g m1a m2 g FT 2 m2 a FT 2 r FT1r M r I
轮不打滑： 联立方程，可解得 FT1 ，FT2，a，β 。
此装置称阿特伍德机——可用于测量重力加速度 g
例4-6 一半径为R，质量为m均质圆盘，平放在粗糙的 水平桌面上。设盘与桌面间摩擦因数为 ，令圆盘最 初以角速度0 绕通过中心且垂直盘面的轴旋转，问它 经过多少时间才停止转动？ 解： 把圆盘分成许多环形 质元，每个质元的质量 dm= red dr，e是盘的厚 度，质元所受到的阻力矩 为 rdmg 。 圆盘所受阻力矩为