多面体欧拉公式的发现一

欧拉柯次公式
欧拉柯次公式又叫欧拉公式，是一个有趣的数学公式，它是由欧拉在18世纪末发现的。

它表明，任何表面上有n个顶点，e条边，f个面的多面体，顶点与边数之积减去边与面
数之积再加2，都等于2。

这就是欧拉公式：V-E+F=2。

欧拉公式最初是发现在多面体上，但它也可以用来描述各种几何形状，如圆柱、环、球等。

它用来表明表面上顶点、边、面的量关系，以及它们的性质之间的关系，表达的是一种性质的定理：顶点的重要性等于边与面的总数。

欧拉公式除了可以用来说明几何形状外，它还被用来检测地理冰川和其他形状的复杂性，
例如盖伊氏玫瑰和莱恩玫瑰，用此可以推导出它们表面上点、线、面的总和及其关系，也
可以使用该公式来检测表面曲率。

由此可见，欧拉公式具有多方面的作用，甚至可以用于东西方文化的交流交融。

总而言之，欧拉公式是一个有趣的数学公式，它具有多方面的应用，不仅可以用于描绘不同几何形状上的量关系，还可以用来检测复杂物体的性质。

它不但具有科学研究价值，而
且可以用于东西方文化的交流。

多面体欧拉公式的发现欧拉公式是数学中的一项重要发现，它描述了多面体的顶点、边和面之间的关系。

发现这个公式的历史可以追溯到18世纪，当时瑞士数学家欧拉在研究多面体时首次提出了这个公式。

多面体是由平面面构成的立体，它可以是凸多面体（所有面都凸），也可以是非凸多面体（至少有一个面是凹的）。

欧拉公式适用于任何类型的多面体，它给出了多面体中顶点、边和面的数量之间的关系。

欧拉公式的数学表达式为：V-E+F=2，其中V表示多面体的顶点数，E 表示边数，F表示面数。

这个公式很简洁，却能揭示多面体的基本性质。

让我们来探索一下欧拉公式的发现过程。

首先，我们从最简单的多面体开始，即立方体。

立方体有8个顶点，12条边和6个面。

代入欧拉公式：8-12+6=2，等号左边的结果与右边的结果相等。

这意味着欧拉公式在立方体上成立。

接下来，让我们考虑一个更复杂的多面体，例如八面体。

八面体有6个顶点、12条边和8个面。

再次代入欧拉公式：6-12+8=2，等号左边的结果与右边的结果相等。

欧拉公式在八面体上同样成立。

通过反复尝试，我们可以发现，无论是简单的立方体还是复杂的八面体，欧拉公式都成立。

这提示我们欧拉公式可能是普适的。

更进一步，我们可以通过归纳法来证明欧拉公式对于任意多面体都成立。

假设对n-1个面的多面体，欧拉公式成立。

现在考虑多面体增加一个面的情况。

如果我们在新面上加上一个新顶点，那么顶点数V将增加1，边数E将增加至少3（因为每个新面至少有3条边相邻），面数F将增加1、根据归纳法的假设，对于n-1个面的多面体，欧拉公式成立，即V-E+F=2(V+1)-(E+3)+(F+1)=V-E+F+2=2+2=4所以对于n个面的多面体，欧拉公式仍然成立。

通过归纳法的推理，我们可以证明欧拉公式对于任意多面体都成立。

总结起来，欧拉公式的发现是通过观察不同形状的多面体并尝试找到它们之间的共同点。

通过代入不同的数值并观察等式的平衡，欧拉发现了顶点、边和面的数量之间的关系，并提出了著名的欧拉公式。

欧拉公式是怎么发现的？欧拉公式指的是近代数学的伟大先驱之一莱昂哈德·欧拉（1707-1783）所发明的一系列公式。

这些公式分布在数学这颗大树的众多分支领域中，比如复变函数中的欧拉幅角公式、初等数论中的欧拉函数公式、拓扑学中的欧拉多面体公式、分式公式等等。

我们在学习中，最先接触到的欧拉公式就是著名的欧拉多面体公式：V-E+F=2。

下面简单介绍下这个公式的发现过程。

早在1639年，法国著名数学家笛卡尔（解析几何学的创始人）就发现了一个规律：不管由多边形围成的凸多面体的外形如何变化，其顶点数（V），棱数（E）和面数（F）都满足一个简单的公式——V-E+F=2。

但在当时这个规律并未广泛流传。

过了一百多年后，欧拉在1750年又重新独立地发现了这个规律，于是这个广为流传的公式被命名为欧拉多面体公式。

欧拉的思路大致是这样的：任意三角形的内角和一定是180°，用弧度表示就是π，这个角度是和三角形的形状和大小无关的。

进而就能发现，任何一个凸n边形的内角和为（n-2）π，这说明凸多边形的内角和是由边数的多少决定的，也和形状、大小等因素无关。

把这个理论推广到空间中若干个多边形围成的凸多面体，又有怎样的性质呢？欧拉首先选择了几个形状简单的多面体进行推理，并将观察所得进行了归纳总结，他发现这些多面体的面角和是由多面体的顶点数决定的。

欧拉又把这个猜想进一步推广，就得到了V-E+F=2的最终结论。

事实上，欧拉多面体公式的证明方法有很多种，比如数学归纳法，球面几何法等。

欧拉是一位不折不扣的数学天才。

但是他的非凡成就也和他对数学的热爱有关。

在欧拉人生的最后7年，他双目完全失明，但是仍然留下了大量数学遗产。

这或许更能说明，为什么数学史上能留下那么多经典的欧拉公式吧。

多面体欧拉公式证明欧拉公式是数学中最著名的定理之一，它被广泛应用于各个领域，如拓扑学、几何学、计算机图形学等。

欧拉公式最初是由瑞士数学家欧拉在1736年发表的一篇论文中提出的，该定理描述了一个多面体的顶点数、边数和面数之间的关系。

在本文中，我们将探讨欧拉公式的证明以及它在几何学和计算机图形学中的应用。

欧拉公式的表述如下：对于一个凸多面体，它的顶点数、边数和面数之间满足以下关系： V-E+F=2其中，V表示多面体的顶点数，E表示多面体的边数，F表示多面体的面数。

证明欧拉公式欧拉公式的证明可以通过归纳法来完成。

首先，我们可以证明对于一个点、一条线和一个面的多面体，欧拉公式成立。

这个多面体只有一个顶点、一条边和一个面，因此：V=1，E=1，F=1将这些值代入欧拉公式中，得到：1-1+1=1这个结论是正确的。

现在，我们考虑一个多面体，它有n个顶点、m条边和k个面。

我们假设对于任意一个顶点数小于n、边数小于m、面数小于k的多面体，欧拉公式都成立。

我们需要证明当顶点数为n、边数为m、面数为k时，欧拉公式也成立。

我们可以从多面体的一个顶点开始考虑。

这个顶点连接了一些边，这些边构成了一些面。

我们可以将这些面分成两类：与这个顶点相邻的面，和不与这个顶点相邻的面。

我们用F1表示与这个顶点相邻的面的个数，用F2表示不与这个顶点相邻的面的个数。

同样地，我们用E1表示与这个顶点相邻的边的个数，用E2表示不与这个顶点相邻的边的个数。

我们可以将多面体分成若干个部分，每个部分都是一个凸多面体。

这些部分可以通过将与这个顶点相邻的面删除而得到。

这些部分的顶点数、边数和面数分别为v1、e1和f1，其中v1<E1。

因此，根据归纳假设，每个部分都满足欧拉公式：v1-e1+f1=2将这些方程相加，得到：v1-e1+f1+v2-e2+f2+...+vk-ek+fk=2k我们发现，这个等式左边的每一项都可以转化成与这个顶点相邻的面、边和顶点的个数。

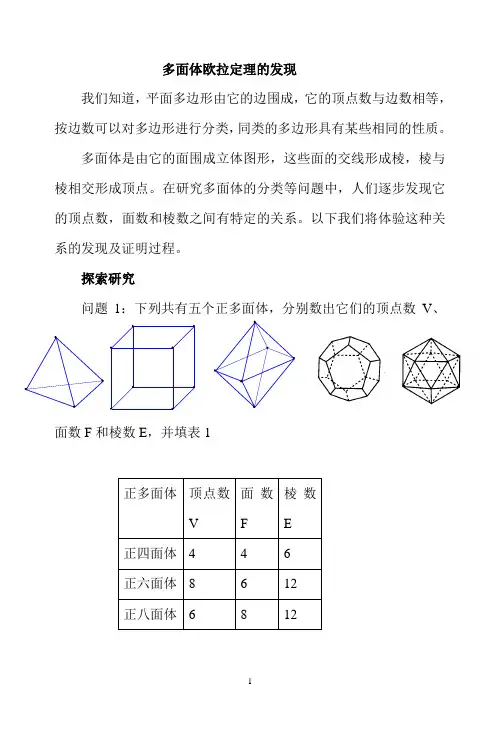
多面体欧拉定理的发现我们知道，平面多边形由它的边围成，它的顶点数与边数相等，按边数可以对多边形进行分类，同类的多边形具有某些相同的性质。

多面体是由它的面围成立体图形，这些面的交线形成棱，棱与棱相交形成顶点。

在研究多面体的分类等问题中，人们逐步发现它的顶点数，面数和棱数之间有特定的关系。

以下我们将体验这种关系的发现及证明过程。

探索研究问题1：下列共有五个正多面体，分别数出它们的顶点数V、面数F和棱数E，并填表1观察表中填出的数据，请找出顶点数V、面数F及棱数E之间的规律。

教师巡视指导，如正十二面体，先定面数E＝12；再定棱数，每个面有5条棱，共有12×5＝60条，由于每条棱都是两个面的公共边，所以上面的计算每条棱被算过两次，于是棱数E＝60/2＝30；最后算顶点数，每个顶点处连有三条棱，所以它共有3V条棱，又因为每条棱连着两个顶点，所以上面的计算每条棱被算过两次，因此实际上只有3V/2条棱，即E＝3V/2，所以V＝20。

表1中多面体的面数F都随顶点数目V的增大而增大吗？（不一定）.请举例说明.（如八面体和立方体的顶点数由6增大到8，而面数由8减小到6）.此时棱的数目呢？（棱数都是一样的）.所以我们得到：棱的数目也并不随顶点数目的增大而增大.大家从表中还发现了其他的什么规律，请积极观察，勇于发言.（当多面体的棱数增加时，它的顶点与面数的变化也有一定规律）.上面的归纳引导去猜想，棱数与顶点数+面数即E与V+F是否有某种关系，请大家按这个方向考察表中的数据，发现并归纳出它们都满足的关系.（积极验证，得出）V+F－E=2以上同学们得到的V+F－E=2这个关系式是由表1中的五种多面体得到，那么这个关系式对于其他的多面体是否也成立吗？请大家尽可能的画出多个其他多面体去验证.（许多同学可能举出前面学过的图形）四棱锥、五棱锥、六棱柱等.（教师应启发学生展开想象，举出更多的例子）一个三棱锥截去含3条棱的一个顶得到的图形、一个立方体截去一个角所得的图形等.好，同学们现在想象，例如：n棱锥在它的n边形面上增加一个“屋顶”或截去含n条棱的一个顶后，刚才的猜想是否成立？能证明吗？所得的多面体的棱数E为3n条，顶点数V为2n个，面数V为2+n 个，因2n +（2+n ）－3n =2,故满足V +F －E =2这个关系式.请继续来观察下面的图形，填表2，并验证得出的公式工V ＋F －E ＝2_A（学生观察，数它们的顶点数V、面数F、棱数E，并填入表2，可能有些同学出错，教师在巡视时要及时给予指导，帮助学生填完）观察你们的数据，请验证这些图形是否符合前面找出的规律吗？其中哪些图形符合？一起来设想问题1和问题2中的图形.在某个橡皮膜上，当橡皮膜变形后，有的地方伸长、有的地方压缩，但不能破裂或折叠，橡皮膜上的图形的形状也跟着改变，这种图形的变化过程我们称之为连续变形.那么请大家试想这些图形中的哪些在连续变形中最后其表面可变为一个球面？问题1中的（1）~（5）和问题2中的（1）个图形表面经过连续变形能变为一个球面.请同学们继续设想问题2中⑴~⑻在连续变形中，其表面最后将变成什么图形？问题2中第⑻个图形；表面经过连续变形能变为环面像以上那些在连续变形中，表面能变为一个球面的多面体叫简单多面体.请大家判断我们前面所学的图哪些是简单多面体？棱柱、棱锥、正多面体、凸多面体是简单多面体.简单多面体的顶点数V、面数F的和与棱数E之间存在规律V+F －E=2.我们将它叫做欧拉公式，以上3个问题的解决让我们体会到了数学家欧拉发现V+F－E=2的过程.那么如何证明欧拉公式呢？请大家打开课本P65的欧拉公式证明方法中的一种，认真体会它的证明思路和其间用到的数学思想.（学生自学、教师查看，发现问题，收集问题下节课处理）在欧拉公式中，令f(p)＝V＋F－E。

§38 研究性课题：多面体欧拉公式的发现（1）一、素质教育目标(一)知识教学点1．简单多面体的V、E、F关系的发现．2．欧拉公式的猜想五种。

3．欧拉公式的证明。

(二)能力训练点1．能通过观察具体简单多面体的V、E、F从中寻找规律。

2．能通过进一步观察验证所得的规律。

3．能从拓朴的角度认识简单多面体的本质。

4．能通过归纳得出关于欧拉公式的猜想。

5．了解欧拉公式的一种证明思路。

(三)德育渗透点1．通过介绍数学家的业绩，培养学生学习数学磊师的献身科学、勇于探索的科学研究精神、激发学生对科学的热爱和对理想的追求。

2．培养学生寻求规律、发现规律、认识规律，并利用规律解决问题的能力．二、教学重点、难点、疑点及解决办法1．教学重点：欧拉公式的发现．2．解决方法：遵循寻求规律——发现规律——认识规律——应用规律的学习过程三、课时安排：2课时。

这是本内容的第1课时。

四、教与学过程设计(一)课题导入瑞士著名数学家欧拉，是数学史上的最多产的数学家，他毕和从事数学研究，他的论著几乎涉及18世纪所有的数学分支。

比如，在初等数学中，欧拉首先将符号正规化: f(x)---函数； e---自然对数的底数； a,b,c---△ABC的三边等．数学中的欧拉公式、欧拉方程、欧拉常数、欧拉方法、欧拉猜想等。

其中欧拉公式e iπ+1=0 ,将数学上的5个常数0、1、i、e、π联在一起；再如就是多面体的欧拉定理V-E+F=2(V、E、F分别表示多面体的顶点、棱和面数。

今天我们就去体验当年的数学大师是如何运用数学思想和方法发现欧拉公式并给予理论上的推理证明等研究活动，希望大家在活动中要充分展开自己的想象，热烈讨论积极交流。

(二)讲授新课1．填表、观察、找规律（1）填表：先从一些常见的多面体出发，对它们的顶点数V、面数F及棱数E，填入表1（P56）；（2）观察：继续观察表1的各组数据，试找出顶点数V、面数F及棱数E的关系如何？（3）分析：（学生讨论）问题1：表1中多面体的面数F都随顶点数V的增大而增大吗？试举例说明。

多面体欧拉公式的历史、建立过程和方法古希腊的毕达哥拉斯学派和柏拉图学派,他们发现了五种正多面体:正四面体、正六面体、正八面体、正十二面体、正二十面体。

欧几里得在《几何原本》中曾试图证明只有这五种正多面体,但没有成功。

在很长的历史时期里,这个问题没有解决。

后来,人们逐渐认识到,依靠角度、长度、面积等几何量的测量或计算,这个问题难以解决,而从多面体的顶点数、棱数和面数的关系入手,有可能获得成功。

1639年,笛卡儿考察了五种正多面体顶点数(V)、棱数(E)和面数(F)的关系,采用不完全归纳法,猜测到:顶点数与面数之和减去棱数,是一个不变量2,也就是:V+F-E=2。

后来,他又用一些简单的多面体来验证自己的猜想,但是没有给出严格的证明,也没有发表。

1751年,欧拉给出了这一性质的一个证明。

后人称它为多面体欧拉公式。

欧拉之所以对这一性质感兴趣,是要用它来做多面体的分类。

[1]但欧拉没有考虑到连续变换下的不变性。

欧拉问题的提出：任意一个三角形的内角和为180度,与三角形的形状无关,进而得到任一个凸n 边形的内角和为π)2(-n ,表明凸多边形的内角和由边数完全决定,而与形状无关。

那么，推广到空间,对于由若干个多边形围成的凸多面体,是否也有某种类似的简单性质呢?欧拉就这样由类比提出了问题。

欧拉证明如下：一个多面体有几种角呢?每条棱处有一个由两个面组成的二面角;每个顶点处,有一个由相交于这个顶点的各个面所围成的角,叫立体角(它的大小等于以立体角顶点为球心的单位球面被这个立体角的各个面所截出的球面多边形的面积的大小)；每个面多边形的每一个内角,叫多面体的一个面角。

欧拉首先考察多面体的所有二面角之和(记为∑δ）及所有立体角之和(记为∑ω),看它们是否有某种简单的性质。

欧拉从最简单的多面体—四面体开始考察。

四面体由四个三角形围成(图1),为了便于计算,欧拉考察了两种退化的情形。

(1)四面体退化成一个三角形和它内部一点与三个顶点所连成的线段(图2)。

多面体欧拉定理定理简单多面体的顶点数V、棱数E及面数F间有关系对于简单多面体，有著名的欧拉公式：V-E+F=2简单多面体即表面经过连续变形可以变为球面的多面体。

多面体欧拉定理式中V表示多面体的顶点数，E表示棱数，F表示面数。

定理一证分析：以四面体ABCD为例。

将它的一个面BCD去掉，再使它变为平面图形，四面体的顶点数V、棱数E与剩下的面数F1变形后都没有变（这里F1=F-1）。

因此，要研究V、E和F的关系，只要去掉一个面，将它变形为平面图形即可。

只需平面图形证明：V+F1-E=1（1）去掉一条棱，就减少一个面，V+F1-E的值不变。

例如去掉BC，就减少一个面ABC。

同理，去掉棱CD、BD，也就各减少一个面ACD、ABD，由于V、F1-E的值都不变，因此V+F1-E的值不变（2）再从剩下的树枝形中，去掉一条棱，就减少一个顶点，V+F1-E的值不变。

例如去掉CA，就减少一个顶点C。

同理去AD就减少一个顶点D，最后剩下AB。

在以上变化过程中，V+F1-E的值不变，V+F1-E=2-0-1=1，所以V+F-E= V+F1-E+1=2。

对任意的简单多面体，运用这样的方法，都是只剩下一条线段。

公式对任意简单多面体都是正确的。

定理意义（1）数学规律：公式描述了简单多面体中顶点数、面数、棱数之间特有的规律；（2）思想方法创新训练：在定理的发现及证明过程中，在观念上，假设它的表面是橡皮薄膜制成的，可随意拉伸；在方法上将底面剪掉，然后其余各面拉开铺平，化为平面图形（立体图→平面图）。

（3）引入拓扑新学科：“拉开图”与以前的展开图是不同的，从立体图到拉开图，各面的形状，以及长度、距离、面积、全等等与度量有关的量发生了变化，而顶点数，面数，棱数等不变。

事实上，定理在引导大家进入一个新几何学领域：拓扑学。

我们用一种可随意变形但不得撕破或粘连的材料（如橡皮波）做成的图形，拓扑学就是研究图形在这种变形过程中的不变的性质。

（4）给出多面体分类方法：在欧拉公式中，令f(p)=V+F-E，f(p)叫做欧拉示性数。

一、课题：多面体欧拉定理的发现三、教学重、难点：欧拉定理的应用．四、教学过程：（一）复习：1．简单多面体的定义；2．欧拉定理；3．正多面体的种类．（二）新课讲解：例1．由欧拉定理证明：正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体这五种． 证明：设正多面体的每个面的边数为，每个顶点连有条棱，令这个多面体的面数为，每个面有条边，故共有条边，由于每条边都是两个面的公共边，故多面体棱数 （1）令这个多面体有个顶点，每一个顶点处有条棱，故共有条棱。

由于每条棱有两个顶点，故多面体棱数 （2）由（1）（2）得：，代入欧拉公式：．∴ （3），∵又，，但，不能同时大于，（若，，则有，即这是不可能的）∴，中至少有一个等于．令，则，∴，∴，∴．同样若可得．例2．欧拉定理在研究化学分子结构中的应用：1996年诺贝尔化学奖授予对发现有重大贡献的三位科学家。

是由60个原子构成的分子，它是形如足球的多面体。

这个多面体有60个顶点，以每一个顶点为一端点都有三条棱，面的形状只有五边形和六边形，计算分子中五边形和六边形的数目． 解：设分子中有五边形个，六边形个。

分子这个多面体的顶点数，面数，棱数，由欧拉定理得：160()(360)22x y ++-⨯= （1），另一方面棱数可由多边形的边数和来表示，得 （2），由（1）（2）得：， ∴分子中五边形有12个，六边形有20个．例3．一个正多面体各个面的内角和为，求它的面数、顶点数和棱数．解：由题意设每一个面的边数为,则，∴，∵，∴,将其代入欧拉公式,得,设过每一个顶点的棱数为,则，得,即（1）,∵，∴,又，∴的可能取值为，,,当或时（1）中无整数解；当,由（1）得,∴, ∴，综上可知:，，.五、小结：1．欧拉定理的应用；2．会用欧拉公式解决简单多面体的顶点数、面数和棱数的计算问题．六、作业：课本第69页 习题9．10第2，3题．一、课题：多面体欧拉定理的发现阅读材料：走近欧拉欧拉(Euler)，瑞士数学家及自然科学家。

多面体欧拉定理的发现本论文主要讲述多面体欧拉定理的发现，证明与完善，及其拓展应用前言多面体欧拉定理是著名瑞士数学家莱昂哈德·欧拉所提出的.欧拉,出生在瑞士的巴塞尔（Basel）城,13岁就进巴塞尔大学读书,得到当时最有名的数学家约翰·伯努利（Johann Bernoulli,1667-1748年）的精心指导．有许多关于欧拉的传说。

比如，欧拉心算微积分就像呼吸一样简单。

有一次他的两个学生把一个复杂的收敛级数的17项加起来，算到第50位数字，两人相差一个单位，欧拉为了确定究竟谁对，用心算进行全部运算，最后把错误找了出来。

欧拉创作文章的速度极快，通常上一本书还没有印刷完，新的手稿就写好了，导致他的写作顺序与出版顺序常常相反，让读者们很郁闷。

而且，收集这些数量庞大的手稿也是一件困难的事情。

瑞士自然科学会计划出一部欧拉全集，这本全集编了将近100年，终于在上个世纪90年代基本完成，没想到圣彼得堡突然又发掘出一批他的手稿，使得这本全集至今仍未完成。

欧拉在数学上的建树很多,对著名的哥尼斯堡七桥问题的解答开创了图论的研究.欧拉还发现,不论什么形状的凸多面体,其顶点数V、棱数E、面数F之间总有V-E+ F=2这个关系.V-E F 被称为欧拉示性数,成为拓扑学的基础概念.以欧拉的名字命名的数学公式、定理等在数学书籍中随处可见, 与此同时,他还在物理、天文、建筑以至音乐、哲学方面取得了辉煌的成就.欧拉还创设了许多数学符号,例如π（1736年）,i（1777年）,e （1748年）,sin和cos（1748年）,tg（1753年）,△x（1755年）,∑（1755年）,f(x)（1734年)等.1733年,年仅26岁的欧拉担任了彼得堡科学院数学教授．1735年,欧拉解决了一个天文学的难题（计算彗星轨道）,这个问题经几个著名数学家几个月的努力才得到解决,而欧拉却用自己发明的方法,三天便完成了．然而过度的工作使他得了眼病,并且不幸右眼失明了,这时他才28岁．据说是因为操劳过度，也有一说是因为观察太阳所致.尽管如此他仍然靠心算完成了大量论文。