从柏拉图多面体到欧拉公式

多面体与欧拉公式多面体是由多个平面多边形所围成的空间几何体，它是几何学中的一个重要研究对象。

欧拉公式是描述多面体面数、边数和顶点数之间关系的一个定理，是欧拉在18世纪提出的，为研究多面体提供了一种重要的工具。

多面体的概念可以追溯到古代希腊，阿基米德曾在他的《多面体》一书中描述了包括正多面体在内的许多多面体。

正多面体是最规整的多面体，每条边的长度、每个面的大小和形状都是相等的。

著名的正多面体有四面体、六面体和十二面体等。

多面体的特点是可以被划分为多个平面多边形，这些多边形的边和顶点都在多面体的表面上。

多面体一般由边、面和顶点三个要素构成。

边是多面体的两个顶点之间的线段，面是多个边所围成的平面区域，而顶点则是多个边和面的交点。

欧拉公式以瑞士数学家欧拉的名字命名，它是多面体几何学中最重要的公式之一、欧拉公式的内容是描述了一个多面体中面、边和顶点的数量关系。

根据欧拉公式，一个多面体的面数、边数和顶点数满足以下关系：面数+顶点数=边数+2这个公式可以应用于所有多面体，无论是规则的还是不规则的。

我们可以通过计算多面体的面数和边数，就可以得出多面体的顶点数。

同时，如果我们已知多面体的面数和顶点数，也可以通过欧拉公式计算出多面体的边数。

欧拉公式的证明可以通过数学归纳法进行。

首先，对于最简单的多面体，四面体，我们可以直接验证欧拉公式成立。

然后，我们可以假设欧拉公式对于n-1个面的多面体成立，即面数+顶点数=边数+2假设现在有一个n个面的多面体，我们可以在其中选取一个面，将它分割成若干个新的面，并且增加若干个额外的顶点和边。

这样，我们就得到了一个n-1个面的多面体，根据归纳假设，它的面数、边数和顶点数满足欧拉公式。

然后，我们再考虑这个n个面的多面体。

由于我们增加了若干个新的面、顶点和边，根据欧拉公式的归纳假设，新的多面体的面数、边数和顶点数满足：(n-1)个面数+新增的1个面+新增的顶点数=(n-1)个边数+新增的边数+2将新增的面数、顶点数和边数代入后，得到：n个面数+新增的顶点数=n个边数+新增的边数+2再将n个面数和新增的顶点数代入到欧拉公式的归纳假设中，得到：(n-1)个面数+新增的顶点数=(n-1)个边数+2由于已知n-1个面的多面体满足欧拉公式，所以有：(n-1)个面数+新增的顶点数=(n-1)个边数+2将这个等式代入前面得到的等式中，即可得出欧拉公式对于n个面的多面体也成立。

简单多面体欧拉公式欧拉公式是简单多面体的一个基本性质，它由数学家欧拉于18世纪提出。

欧拉公式给出了简单多面体的面（F）、边（E）和顶点（V）之间的关系，具体表述如下：F+V-E=2（其中F、V、E分别表示多面体的面、顶点和边的个数）这个公式虽然简短，却包含了许多有趣的性质和应用。

下面我们将详细讨论欧拉公式及其相关的一些主要内容。

首先，我们来证明欧拉公式。

假设一个简单多面体有n个面，m个边和v个顶点，可以通过以下步骤证明欧拉公式。

1.每个面都是由若干个边围成的，而每个边都是由两个面共享的，所以每个面都至少有3个边。

因此，n个面至少有3n个边。

2.每个边都是由两个顶点连接的，所以每个边都至少连接2个顶点。

因此，m个边至少连接2m个顶点。

3.由于每个顶点都至少有3个边连接，所以v个顶点至少有3v个边。

根据以上三个推论，我们可以得到：3n≤2m2m≤3v将这两个不等式相加，得到：3n+2m≤5m，进一步化简可得：3n+2m≤5m因此，我们有：3n+3m-3m+2m≤5m，整理后得到：3n+3m-5m≤3m，进一步得到：3(n-m)≤3m，即：n-m≤m由于n和m均为正整数，所以n-m≤m一定成立。

将n-m=v代入上式，可以得到：v≤2m再将v代入欧拉公式F+V-E=2中，可以得到：F+(2m)-m=2，化简之后可以得到：F=2+m综上所述，我们证明了欧拉公式F+V-E=2接下来，我们来讨论一些与欧拉公式相关的性质和应用。

1.欧拉公式适用于所有的简单多面体，包括凸多面体和非凸多面体。

凸多面体是指其任意两点之间的直线都位于多面体的内部的多面体，而非凸多面体则不满足这一条件。

2.欧拉公式可以用于检验多面体的正确性。

例如，如果在计算多面体的面、顶点和边的个数时，结果不满足欧拉公式，即F+V-E≠2，则说明计算存在错误。

3.欧拉公式可以用于构造简单多面体。

给定一定的面、顶点和边的个数，可以通过欧拉公式来确定是否存在满足这些条件的简单多面体，并且可以帮助我们找到构造多面体的方法。

欧拉定理公式
在任何一个规则球面地图上，用R记区域个数，V记顶点个数，E记边界个数，则R+V-E=2，这就是欧拉定理。

它于1640年由Descartes首先给出证明，后来Euler（欧拉）于1752年又独立地给出证明，我们称其为欧拉定理，在国外也有人称其为Descartes定理。

第一个欧拉公式的严格证明，由20岁的柯x给出，大致如下：从多面体去掉一面，通过把去掉的面的边互相拉远，把所有剩下的面变成点和曲线的平面网络。

不失一般性，可以假设变形的边继续保持为直线段。

正常的面不再是正常的多边形即使开始的时候它们是正常的。

但是，点，边和面的个数保持不变，和给定多面体的一样（移去的面对应网络的外部。

）
重复一系列可以简化网络却不改变其欧拉数（也是欧拉示性数）的额外变换。

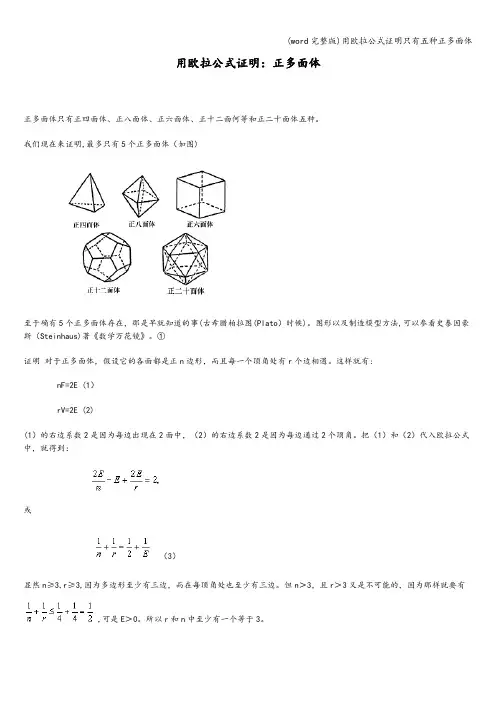
用欧拉公式证明：正多面体
正多面体只有正四面体、正八面体、正六面体、正十二面何等和正二十面体五种。

我们现在来证明,最多只有5个正多面体（如图)
至于确有5个正多面体存在，那是早就知道的事(古希腊柏拉图(Plato）时候)。

图形以及制造模型方法,可以参看史泰因豪斯（Steinhaus)著《数学万花镜》。

①
证明对于正多面体，假设它的各面都是正n边形，而且每一个顶角处有r个边相遇。

这样就有:
nF=2E (1）
rV=2E (2)
(1）的右边系数2是因为每边出现在2面中，（2）的右边系数2是因为每边通过2个顶角。

把（1）和（2）代入欧拉公式中，就得到：
或
（3）
显然n≥3,r≥3,因为多边形至少有三边，而在每顶角处也至少有三边。

但n＞3，且r＞3又是不可能的，因为那样就要有 ,可是E＞0。

所以r和n中至少有一个等于3。

设n=3,那末，因此r=3,4，5，由是E=6，12,30，而F=4，8，20,这就给出了正四面体，正八面体和正二十面体。

设r=3，那末，因此n=3,4，5,由是E=6，12，30，而F=4，6，12，这就给出了正四面体,正六面体(即立方体）和正十二面体.。

说文解图二：柏拉图多面体说文：我们在日常生活中接触很多立体.在众多立体之中,最有"规律"的便是"柏拉图多面体".。

它并不是由柏拉图所发明，但是却是由柏拉图及其追随者对它们所作的研究而得名，由于它们具有高度的对称性及次序感，因而通常被称为正多面体！为什么会说柏拉图立体很有规律呢？这是因为每一个柏拉图立体,都只是由一种正多边形砌成的.数学家证明了世上只能存在以下五种柏拉图立体.正四面体(Tetrahedron)由四个等边三角形组成正六面体(cube / hexahedron)由六个正方形组成正八面体(octahedron)由八个等边三角形组成正十二面体(dodecahedron)由十二个正五边形组成正二十面体(icosahedron)由二十面等边三角形组成柏拉图的宇宙观基本上是一种数学的宇宙观。

他设想宇宙开头有两种直角三角形，一种是正方形的一半，另一种是等边三角形的一半。

从这些三角形就合理地产生出四种正多面体，这就组成四种元素的微粒。

火微粒是正四面体，气微粒是正八面体，水微粒是正二十面体，土微粒是立方体。

第五种正多面体是由正五边形形成的十二面体，这是组成天上物质的第五种元素，叫做以太。

整个宇宙是一个圆球，因为圆球是对称和完善的，球面上的任何一点都是一样。

宇宙也是活的，运动的，有一个灵魂充溢全部空间。

解图：为什么只有五种正多面体呢？1、几何证明：柏拉图多面体每一个都是凸的，并且在每一个顶点处交会着相同数目、相似、正的凸多边形。

要理解为什么只有五个柏拉图多面体是相当简单的，这是因为在每一个顶点处交会着至少三个面才能构造出一个立体图形，而且围绕每一个顶点的面的角度和不能等于或超过360°，否则所得的面将是平的或是凹的。

所以，最多只有正五边形组成。

因为正六边形的每个内角是120°，三个正六边形为360°，故不成立！2、欧拉公式证明：假设一个正多面体共有V 个顶点、F 块面及E 条边;欧拉公式：V + F - E = 2每一块面均为正n 边形，且每一个顶点共有m 块面的顶点相连。

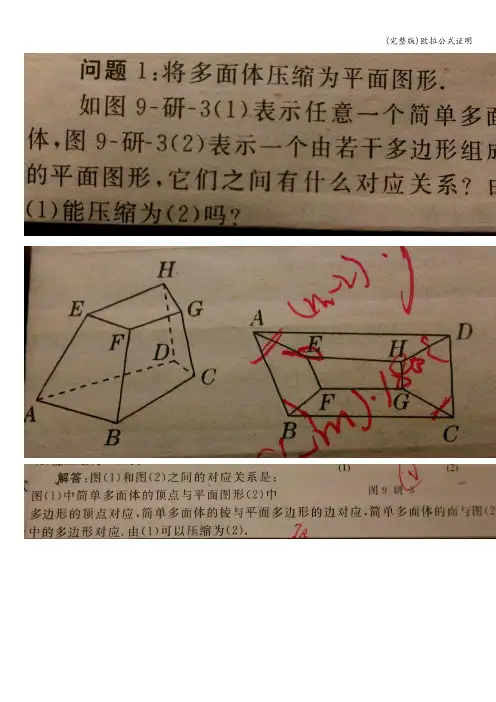
多面体欧拉定理：
定理简单多面体的顶点数V、棱数E及面数F间有关系对于简单多面体，有著名的欧拉公式：V—E+F=2简单多面体即表面经过连续变形可以变为球面的多面体。

欧拉定理：
定理简单多面体的顶点数V、面数F及棱数E间有关系V+F-E=2;
公式描述了简单多面体中顶点数、面数、棱数之间特有的规律。

定理的证明：
分析：以四面体ABCD为例.
将它的一个面BCD去掉,再使它变为平面图形，四面体的顶点数V、棱数E 与剩下的面数F1变形后都没有变（这里F1=F-1）。

因此，要研究V、E 和F的关系,只要去掉一个面,将它变形为平面图形即可。

只需平面图形证明：V+F1-E=1；
(1)去掉一条棱,就减少一个面，V+F1-E的值不变。

例如去掉BC，就减少一个面ABC。

同理，去掉棱CD、BD,也就各减少一个面ACD、ABD，由于V、F1—E的值都不变,因此V+F1-E的值不变；
(2)再从剩下的树枝形中,去掉一条棱，就减少一个顶点,V+F1-E的值不变.例如去掉CA，就减少一个顶点C.同理去AD就减少一个顶点D，最后剩下AB.
在以上变化过程中，V+F1—E的值不变,V+F1-E=2—0—1=1,所以 V+F—E= V+F1-E+1=2。

对任意的简单多面体，运用这样的方法,都是只剩下一条线段。

公式对任意简单多面体都是正确的。

欧拉定理又一证法：
多面体，设顶点数V,面数F,棱数E。

剪掉一个面，将其余的面拉平，使它变为平面图形, 我们在两个图中求所有面的内角总和Σα。

一方面，利用面求内角总和.。

并不是由柏拉图所发明，但是却是由柏拉图及其追随者对它们所作的研究而得名，由于它们具有高度的对称性及次序感，因而通常被称为正多面体，但是，在这里，我们仍以柏拉图多面体称之，以免与其它有规则的多面体产生混淆。

柏拉图多面体所有的面都是不自交、以直线段为边长的正凸多边形平面，每一种多面体都只有一种正多边形的表面，而且在每一个顶点处都有相同数目的面交会。

不仅在每一个顶点处都有相同数目的面交会，而且在每一个顶点处所有交会的面的内角之总和会相等。

简介熟悉柏拉图多面体的最佳方法莫过于经由构造模型并透过模型研究它们。

下图表示一种称之为”展开图”的个别柏拉图多面体平面排列图示。

为了构造柏拉图多面体的模型，一组类似的展开图必须被描绘在适当的材料上。

同学可以将本资料所附之多面体的展开图直接剪下或经放大、缩小影印在合适的漂亮纸张上。

如果材料不方便影印，您也可以依样绘制或把影印展开图并贴在所用材料上。

Albrecht Durei早在1525年，于他所著的《Unterweisung der Messung Mit dem Zirkel und Richtsheit》一书中，给出了几个多面体的展开图。

编辑本段为什么只有五个柏拉图多面体很容易看出柏拉图多面体每一个都是凸的，并且在每一个顶点处交会着相同数目、相似、正的凸多边形。

要理解为什么只有五个柏拉图多面体是相当简单的，这是因为在每一个顶点处交会着至少三个面才能构造出一个立体图形，而且围绕每一个顶点的面的角度和不能等于或超过360°，否则所得的面将是平的或是凹的。

具有最少边数的正多边形是正三角形，三个如此的多边形可以使它们交会在一个顶点上，接下来，加入第四个面，如此，每三个面就会交会在图形的四个顶点处之一。

由于这个图形有四个全等的面，故称之为正四面体(TETRAHEDRON)。

四个正三角形可以使它们交会在一个顶点上，而且加入四个面之后，在图形的六个顶点处都会有四个面交会在这里。

多面体欧拉公式的历史、建立过程和方法古希腊的毕达哥拉斯学派和柏拉图学派,他们发现了五种正多面体:正四面体、正六面体、正八面体、正十二面体、正二十面体。

欧几里得在《几何原本》中曾试图证明只有这五种正多面体,但没有成功。

在很长的历史时期里,这个问题没有解决。

后来,人们逐渐认识到,依靠角度、长度、面积等几何量的测量或计算,这个问题难以解决,而从多面体的顶点数、棱数和面数的关系入手,有可能获得成功。

1639年,笛卡儿考察了五种正多面体顶点数(V)、棱数(E)和面数(F)的关系,采用不完全归纳法,猜测到:顶点数与面数之和减去棱数,是一个不变量2,也就是:V+F-E=2。

后来,他又用一些简单的多面体来验证自己的猜想,但是没有给出严格的证明,也没有发表。

1751年,欧拉给出了这一性质的一个证明。

后人称它为多面体欧拉公式。

欧拉之所以对这一性质感兴趣,是要用它来做多面体的分类。

[1]但欧拉没有考虑到连续变换下的不变性。

欧拉问题的提出：任意一个三角形的内角和为180度,与三角形的形状无关,进而得到任一个凸n 边形的内角和为π)2(-n ,表明凸多边形的内角和由边数完全决定,而与形状无关。

那么，推广到空间,对于由若干个多边形围成的凸多面体,是否也有某种类似的简单性质呢?欧拉就这样由类比提出了问题。

欧拉证明如下：一个多面体有几种角呢?每条棱处有一个由两个面组成的二面角;每个顶点处,有一个由相交于这个顶点的各个面所围成的角,叫立体角(它的大小等于以立体角顶点为球心的单位球面被这个立体角的各个面所截出的球面多边形的面积的大小)；每个面多边形的每一个内角,叫多面体的一个面角。

欧拉首先考察多面体的所有二面角之和(记为∑δ）及所有立体角之和(记为∑ω),看它们是否有某种简单的性质。

欧拉从最简单的多面体—四面体开始考察。

四面体由四个三角形围成(图1),为了便于计算,欧拉考察了两种退化的情形。

(1)四面体退化成一个三角形和它内部一点与三个顶点所连成的线段(图2)。