多面体欧拉公式与球

名师辅导 立体几何 第10课 正多面体、球（含答案解析）●考试目标 主词填空1.多面体欧拉公式（1）欧拉公式V ＋F －E ＝2，是描述简单多面体的顶点数、面数、棱数之间特有规律的一个公式.2. 球的概念和性质（1）定义：半圆以它的直径为旋转轴旋转所成的曲面叫做球面，球面所围成的几何体叫球体，简称球.3.球面的距离 在球面上，两点之间的最短连线的长度，就是经过这两点大圆在这两点间的一段劣弧的长度，这个弧长叫做两点的球面距离.4.球的表面积和体积球的表面积和体积都是球半径R 的函数.(1)半径为R 的球表面积公式是：S ＝4πR 2,(2)半径为R 的球体积公式是：S =334R π.●题型示例 点津归纳【例1】 已知铜的单晶的外形是简单几何体，单晶铜有三角形和八边形两种晶面，如果铜的单晶有24个顶点，每个顶点处都有三条棱，计算单晶铜的两种晶面的数目.【解前点津】 设三角形晶面有x 个，八边形晶面有y 个.则单晶铜的面数F =x +y ,且棱数E =21(3x +8y ). 又因为铜的单晶的顶点数V =24,且每个顶点处都有3条棱所以棱数 E =21×（3×24）＝36 由欧拉公式得 24+(x +y )-36=2 所以x +y =14,再由21(3x +8y )=36 可解得x =8,y =6所以单晶铜的三角形晶面有8个，八边形晶面有6个.【解后归纳】 本题考查多面体，凸多面体和多面体的欧拉定理及其应用.【例2】 一个简单多面体共有16个顶点，每个顶点都引出3条棱，且只有三角形和五边形两种面，求该简单多面体中三角形和五边形的数目各是多少?【解前点津】 设该简单多面体中三角形和五边形数目分别为x 个、y 个，一方面可根据欧拉定理计算棱数，另一方面可由各面边数计算棱数，这样可以得到一个二元一次方程组，求解即可.【规范解答】 设三角形有x 个，五边形有y 个，∵共有16个顶点，每个顶点引出三条棱，∴棱数E =2316⨯=24, 一方面相邻两个面的两条边重合为一条棱， ∴棱数为253y x +,∴253y x +=24 ① 另一方面，由题意知面数F =x +y ，由欧拉定理得：16+(x +y )-24=2 ②由①②联立可得：x =1,y =9，即三角形面有1个，五边形面有9个.【例3】 一个圆锥形漏斗口的内周长为8πcm ．漏斗深9.6cm ，将一个球放进漏斗里，球的最高点比漏斗口所在平面高出2.4cm ，求球的体积.【解前点津】 作出轴截面图.【规范解答】 作共同的轴截面图(如图)，得等腰△PAB 和圆O ，球的最高点C ，球心O 和圆锥顶点P 三点共线，D =AB ∩PC ,依题设：PD =9.6,CD =2.4,AD =428=ππ. 过C 作A 1B 1∥AB 与PA 、PB 的延长线分别交于点A 1、B 1，则A 1B 1与圆O 相切于C . 且有25.16.9121===PD PC AD C A . ∴A 1C =1.25AD =5.PA 1=.13221=+PC C A记PA 1与圆O 的切点为E ，则A 1C =A 1E ，且△PEO ∽△PCA 1， 得C A OE PC PE 1=,PE =PA 1-A 1E =13-5=8, ∵OE =3101=⋅PC C A PE , 即得球半径R =310,所以它的体积为814000343π=π=R V (cm 3). 【解后归纳】 作出圆锥与球共同的轴截面，则圆锥与球的重要几何量与几何关系都在这一平面图形上充分展现出来了，通过对此平面图形的分析，即可求出球半径，从而求得球体积.【例4】 在北纬45°的纬度圈上有A 、B 两点,它们分别在东经70°与东经160°的经度圈上，设地球半径为R ，求A 、B 两点的球面距离.【规范解答】 如图,设北纬45°圈的圆为O 1,地球中心为O ,则∠AO 1B =160°-70°=90°,∠OBO 1=45°,OB =R .∴O 1B =O 1A =R 22,AB =R , 连接AO ,AB ,则AO =BO =AB =R , ∴∠AOB =60°,∴=61·2πR =31πR . 故A 、B 两点间的球面距离为31πR . 【解后归纳】 为求A 、B 两点间球面的距离,要把它组织到△AOB 中去分析，只要求得∠AOB 的度数便可求得球面距离，注意余弦定理的应用.●对应训练 分阶提升一、基础夯实1.正三棱锥是正四面体的 ( )A.充分不必要条件B.必要不充分条件C.充要条件D.不充分不必要条件2.正六面体的顶点数V 和棱数E 分别是 ()例3题图例4题图A.V =8,E =12B.V ＝12，E ＝8C.Ｖ＝6，E ＝8D.V ＝6，E ＝103.球面上有3个点，其中任意两点的球面距离都等于大圆周长的61，经过这3个点的小圆的周长为4π，那么球的半径为 ( ) A.43 B.23 C.2 D. 3 4.正十二面体的面是正三角形，且每一个顶点为其一端都有五条棱，则其顶点数V 和棱数E 的值应是( )A.V ＝30，E ＝12B.Ｖ＝12，E ＝30C.Ｖ＝32，E ＝10D.Ｖ＝10，E ＝325.在底面直径为2的等边圆柱中,分别以两底为底面,以圆柱的轴上任一点为顶点的两个圆锥的体积之和是(轴截面为正方形的圆柱称为等边圆柱) ( ) A.34π B.32π C. 3π D.值不确定 6.设正多面体的每个面都是正n 边形，以每个顶点为端点的棱有m 条，棱数是E ，面数是F ，顶点数是V ，则它们之间的关系不正确的是 ( )A.nF =2EB.mV =2EC.V ＋F ＝E ＋2D.mF =2E7.把一个半径为R 的实心铁球熔化后铸成两个小球(不计损耗)，两个小球的半径之比为1∶2，则其中较小球半径为 ( ) A.R 31 B.R 333 C.R 5253 D.R 33 8.在地球表面北纬60°线上有两点，它的经度差为180°，则A 、B 两点的纬度线的距离与A 、B 两点的球面距离之比为 ( )A.1∶3B.2∶3C.3∶2D.3∶59.半径为R 的三个球两两外切放置桌面上，与这三个球都外切的第四个小球也放在桌面上，则小球的半径为 ( )A.RB.21RC.31R D.R 32 10.已知过球面上三点A 、B 、C 的截面与球心距离等于球半径的一半，且AB ＝BC ＝CA ＝2，则球的半径等于 ( )A.1B.34C.32 D.332 二、思维激活11.一个简单多面体每个顶点处都有三条棱，则它的顶点数V 和面数F 的关系是 .12.半球内有一内接正方体，则这半球的全面积与正方体的全面积之比为 .13.在120°的二面角内，放一个半径为5 cm 的球切两半平面于A 、B 两点，那么这两个切点在球面上最短距离是 .14.地球半径为6 370km ，地球表面北纬30°圈上有A 、B 两个卫星地面接收站，它们在北纬 30°圈上的距离是336370πkm ，则这两地间的经度差是 . 三、能力提高15.求证：正四面体的二面角与正八面体的二面角互为补角.16.制作两个正四面体的模型，再把它们拼成一个六面体，观察一下这个六面体是否为正六面体.17.C 70分子有70个顶点，以每个顶点为一端都有3条棱，各面是五边形或六边形，求C 70分子中五边形和六边形的个数.18.如图所示，三棱锥V —ABC 中，VA ⊥底面ABC ，∠ABC ＝90°.(1)求证：V 、A 、B 、C 四点在同一球面上.(2)过球心作一平面与底面内直线AB 垂直.求证：此平面截三棱锥所得的截面是矩形.19.如图所示,在棱长为a 的正方体AC 1中求,(1)过BD 1所作的最小截面面积;(2)过BD 1所作截面周长最小时的截面面积.第10课 正多面体、球习题解答1.B 正四面体为正三棱锥，而正三棱锥不一定为正四面体.2.A 由欧拉定理可得.3.B 设球半径为R ，小圆半径为r ，则2πr =4π，∴r =2.设这三点为A 、B 、C ，球心为O ，则根据球面距离意义可知∠AOB =∠BOC =∠COA =362π=π. 第18题图第19题图∴△ABC 为正△且边长为R ,又r 为△ABC 外接圆半径.∴r =R AB 3333=,∴R =3r =23. 4.B 顶点为12个，棱数E =30.5.B 画图运用等边圆柱的概念即得.6.D 只有mF =2E 不正确.7.B 设较小的半径为r ， ∴34πr 3+34π(2r )3=34πR 3，∴r =333R . 8.C 2:3360cos 221RR π︒⋅π⋅. 9.C 设第四个小球的半径为x ， ∴x +.)32232()(22R R R x =⋅⋅-+ 解得：x =3R . 10.B 32232222⋅⋅=⎪⎭⎫ ⎝⎛-R R ，∴R =34. 11.V =2F -4 利用多面体结构特点易知. 12.43π 如图设正方体棱长为x ，球半径为R ， ∴R =.262222x x x =⎪⎪⎭⎫ ⎝⎛+ S 半球全=21·4πR 2+πR 2=3πR 2， S 正方体=6x 2=6·262⎪⎪⎭⎫ ⎝⎛R =4R 2， ∴.434322π=π=R R S S 正方体半球全 13.35π 两切点对球心的张角为3π，∴球面距为35π . 14.120° 北纬30°圈的半径为6370·23, ∴6370·23·θ=6370·23π， ∴θ=32π，即经度差为120°. 15.设正四面体有S —ABC 和正八面体AC 的棱长都为a ,正四面体的二面角为α，正八面体的二面角为2β. 易求得tan α＝22 (0<α<2π). 在正八面体AC 中，连EF 交截面ABCD 于O ，取AB 的中点G .连EG 、FG 、OG ，则EG ⊥AB ,FG ⊥AB ,所以∠EGF 为二面角的平面角.由对称性知∠EGO =∠OGF ＝β，又EG =23a ,GO =21a ,∴EO =a 22. 第12题图解∴tan ∠EGO =tan ∠β=2222=aa . ∴tan2β＝22tan 1tan 22-=β-β(0<2β<π) ∴α与β互补. 16.不是正六面体，正六面体即为正方体.17.设C 70分子中五边形和六边形分别有x 个和y 个，C 70分子这个多面体的顶点数V ＝70，面数F =x +y ,棱数E =21(3×70) ，根据欧拉公式，可得70+(x +y )-21(3×70)=2, 由棱数相等有：21(5x +6y )= 21×(3×70). 解得：x =12,y =25∴C 70分子中五边形有12个，六边形有25个.18.(1)取VC 的中点M ，∵VA ⊥底面ABC ，∠ABC ＝90°，∴BC ⊥VB ，在Rt △VBC 中，M 为斜边 VC 的中点.∴MB ＝MC ＝MV ，同理在Rt △VAC 中，MA ＝MV ＝MC ，∴MV ＝MC ＝MA ＝MB ，∴V 、A 、B 、C 四点在同一圆面上，M 是球心.(2)取AC ，AB ，VB 的中点分别为N 、P 、Q ，连结NP 、PQ 、QM 、MN .则MNPQ 就是垂直于AB 的三棱锥V —ABC 的截面，易证PQMN 是平行四边形，又VA ⊥BC ，PQ ∥VA ，NP ∥BC ，∴QP ⊥PN ，故截面MNPQ 是矩形.19.这是一道有关立体几何最值问题的题目,比较综合,我们可对本题作简单分析:(1)设经过BD 1的截面为BMD 1N ,因为正方体相对侧面平行,故BMD 1N 是平行四边形,这样S 截=2S △BMD 1显然欲使S 截最小,只需S △BMD 1最小,而BD 1为定值,故只需M 到BD 1的距离最小,M 可在AA 1上移动,所以这个问题可转化为求异面直线AA 1与BD 1之间的距离,而求异面直线间的距离又可化为线面间的距离(AA 1与面BB 1D 1D 间的距离)(2)沿侧棱将侧面AD 1与侧面AB 1展开如图所示,D 1M +MB 的最小值就是侧面展开图中的D 1B ,设D 1B 与AA 1交于M ,由于侧面为全等的正方形，故M 为AA 1的中点,同理N 为CC 1的中点,此时MB ∥ND 1为所求截面.第19题图解。

多面体的欧拉公式球(总4页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--多面体的欧拉公式球多面体的欧拉公式：一．重点、难点提示1．多面体的概念若干个平面多边形围成的几何体叫做多面体．把多面体的任何一个面伸展为平面，如果所有其他各面都在这个平面的同侧，这样的多面体叫做凸多面体．一个多面体至少有四个面．2．正多面体每个面都是有相同边数的正多边形，且以每个顶点为其一端都有相同数目的棱的凸多面体叫做正多面体．正多面体分别是正四面体、正六面体、正八面体、正十二面体和正二十面体共五种，其中正四面体、正八面体和正二十面体的各个面都是全等的正三角形，正六面体又叫做正方体，其各个面都是全等的正方形而正十二面体的各面是全等的正五边形．3. 欧拉公式如果简单多面体的顶点数为V，面数为F，棱数为E，那么V+F-E=2．二．考点指要理解多面体、凸多面体、简单多面体和正多面体的概念，能运用欧拉公式进行有关的判断和计算．球：一．重点、难点提示1．球面的概念半圆以它的直径为旋转轴，旋转所成的曲面叫做球面，半圆的圆心叫做球心．连结球心和球面上任意一点的线段叫做球半径，连结球面上两点且经过球心的线段叫做球的直径．球面也可以看作与定点(圆心)的距离等于定长(半径)的所有点的集合，如果一个球的球心为O，我们可以把这个球记作球O．2．球的概念球面所围成的几何体叫做球体，简称球．3．球的截面及其性质用一个平面截一个球，截面是圆面，球的截面有如下性质：(1)球心与截面圆心的连线垂直于截面；(2)球心到截面的距离d与球的半径及及截面的半径r有下面的关系：。

4．球面上的大圆和小圆球面被经过球心的平面截得的圆叫做大圆，被不经过球心的截面截得的圆叫做小圆，地球上的赤道就是一个大圆，北极圈就是一个小圆。

球面上两点距离的概念：在球面上，两点之间的最短连线的长度即经过这两点的大圆在这两点间的一段劣弧的长度，叫做两点的球面距离。

证明欧拉公式欧拉公式简单多面体的顶点数V、面数F及棱数E间有关系V+F-E=2这个公式叫欧拉公式。

公式描述了简单多面体顶点数、面数、棱数特有的规律。

认识欧拉欧拉，瑞士数学家，13岁进巴塞尔大学读书，得到著名数学家贝努利的精心指导．欧拉是科学史上最多产的一位杰出的数学家，他从19岁开始发表论文，直到76岁，他那不倦的一生，共写下了886本书籍和论文，其中在世时发表了700多篇论文。

彼得堡科学院为了整理他的著作，整整用了47年。

欧拉著作惊人的高产并不是偶然的。

他那顽强的毅力和孜孜不倦的治学精神，可以使他在任何不良的环境中工作：他常常抱着孩子在膝盖上完成论文。

即使在他双目失明后的17年间，也没有停止对数学的研究，口述了好几本书和400余篇的论文。

当他写出了计算天王星轨道的计算要领后离开了人世。

欧拉永远是我们可敬的老师。

欧拉研究论著几乎涉及到所有数学分支，对物理力学、天文学、弹道学、航海学、建筑学、音乐都有研究！有许多公式、定理、解法、函数、方程、常数等是以欧拉名字命名的。

欧拉写的数学教材在当时一直被当作标准教程。

19世纪伟大的数学家高斯（Gauss，1777-1855）曾说过“研究欧拉的著作永远是了解数学的最好方法”。

欧拉还是数学符号发明者，他创设的许多数学符号，例如π，i，e，sin，cos，tg，∑，f (x)等等，至今沿用。

欧拉不仅解决了彗星轨迹的计算问题，还解决了使牛顿头痛的月离问题。

对著名的“哥尼斯堡七桥问题”的完美解答开创了“图论”的研究。

欧拉发现，不论什么形状的凸多面体，其顶点数V、棱数E、面数F之间总有关系V+F-E=2，此式称为欧拉公式。

V+F-E即欧拉示性数，已成为“拓扑学”的基础概念。

那么什么是“拓扑学”？欧拉是如何发现这个关系的？他是用什么方法研究的？今天让我们沿着欧拉的足迹，怀着崇敬的心情和欣赏的态度探索这个公式......欧拉定理的意义（1）数学规律：公式描述了简单多面体中顶点数、面数、棱数之间特有的规律（2）思想方法创新：定理发现证明过程中，观念上，假设它的表面是橡皮薄膜制成的，可随意拉伸；方法上将底面剪掉，化为平面图形（立体图→平面拉开图）。

第 48 讲 多面体、欧拉公式与球（第课时）多面体、欧拉公式与球 ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧多面体的内切球体积面积计算球面距离截面球的性质球的概念球正多面体的概念欧拉公式多面体的概念多面体重点：1．多面体、正多面体的概念；2．欧拉公式；3．球的概念和性质。

难点：1．球的性质及应用；2．有关球的组合体。

2．了解多面体的欧拉公式；3．了解球的概念，掌握球的性质4. 掌握球的表面积、体积公式。

2．有关球的考查一般以小题出现。

由若干个平面多边形围成的几何体，叫做多面体。

围成多面体的各个多边形叫做面，两个面的公共边叫棱，棱的端点叫顶点，不在同一个面内的两个顶点间的线段叫对角线。

有n 个面的多面体叫n 面体（4≥n ）。

凸多面体：若把一个多面体的任意一个面沿展成平面，其余各面都在这个平面的同侧时，则称这个多面体为凸多面体。

简单多面体：表面能通过连续变形变为球面的多面体，叫做简单多面体。

2．欧拉公式对于简单多面体，有： 顶点数（V ）+面数(F)-棱数（E ）= 2 。

例．一个正n 面体共有8个顶点，每个顶点处共有3条棱，则n 等于 （ ） A . 4 ； B . 5 ； C . 6 ； D . 7 。

分析： 先计算正n 面体的棱数，然后应用欧拉公式来解。

解：由题意有 8=V ，12283=⨯=E ，则 682122=-+=-+=V EF ，故选C 。

例．已知铜的单晶的外形是简单几何体，单晶铜有三角形和八边形两种晶面，如果铜的单晶有24个顶点，每个顶点处都有3条棱，计算单晶铜的两种晶面的数目。

解 设：三角形晶面有x 个，八边形晶面有y 个。

3．正多面体⑴ 定义：每个面都是有相同边数的正多边形，且以每个顶点为其一端都有相同数目的棱的凸多面体，叫做正多面体。

⑵4．球 ⑴ 定义① 球面: 半圆绕它的直径旋转一周所生成的曲面叫做球面。

② 球: 球面围成的几何体叫球。

多面体欧拉定理定理简单多面体的顶点数V、棱数E及面数F间有关系对于简单多面体，有著名的欧拉公式：V-E+F=2简单多面体即表面经过连续变形可以变为球面的多面体。

多面体欧拉定理式中V表示多面体的顶点数，E表示棱数，F表示面数。

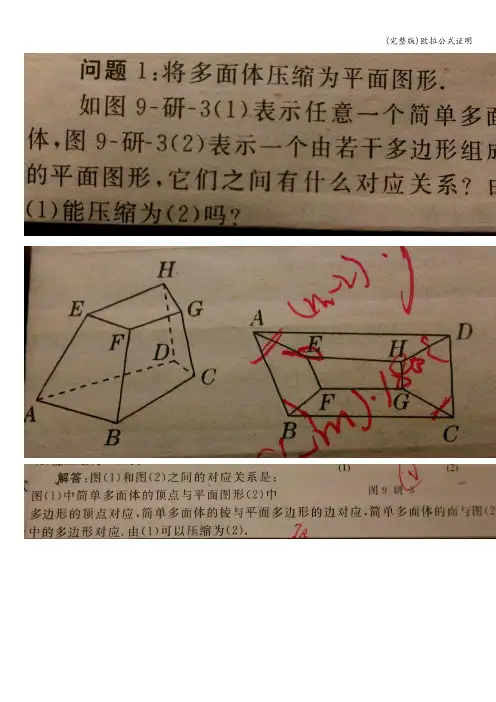
定理一证分析：以四面体ABCD为例。

将它的一个面BCD去掉，再使它变为平面图形，四面体的顶点数V、棱数E与剩下的面数F1变形后都没有变（这里F1=F-1）。

因此，要研究V、E和F的关系，只要去掉一个面，将它变形为平面图形即可。

只需平面图形证明：V+F1-E=1（1）去掉一条棱，就减少一个面，V+F1-E的值不变。

例如去掉BC，就减少一个面ABC。

同理，去掉棱CD、BD，也就各减少一个面ACD、ABD，由于V、F1-E的值都不变，因此V+F1-E的值不变（2）再从剩下的树枝形中，去掉一条棱，就减少一个顶点，V+F1-E的值不变。

例如去掉CA，就减少一个顶点C。

同理去AD就减少一个顶点D，最后剩下AB。

在以上变化过程中，V+F1-E的值不变，V+F1-E=2-0-1=1，所以V+F-E= V+F1-E+1=2。

对任意的简单多面体，运用这样的方法，都是只剩下一条线段。

公式对任意简单多面体都是正确的。

定理意义（1）数学规律：公式描述了简单多面体中顶点数、面数、棱数之间特有的规律；（2）思想方法创新训练：在定理的发现及证明过程中，在观念上，假设它的表面是橡皮薄膜制成的，可随意拉伸；在方法上将底面剪掉，然后其余各面拉开铺平，化为平面图形（立体图→平面图）。

（3）引入拓扑新学科：“拉开图”与以前的展开图是不同的，从立体图到拉开图，各面的形状，以及长度、距离、面积、全等等与度量有关的量发生了变化，而顶点数，面数，棱数等不变。

事实上，定理在引导大家进入一个新几何学领域：拓扑学。

我们用一种可随意变形但不得撕破或粘连的材料（如橡皮波）做成的图形，拓扑学就是研究图形在这种变形过程中的不变的性质。

（4）给出多面体分类方法：在欧拉公式中，令f(p)=V+F-E，f(p)叫做欧拉示性数。

多面体欧拉定理：
定理简单多面体的顶点数V、棱数E及面数F间有关系对于简单多面体，有著名的欧拉公式：V—E+F=2简单多面体即表面经过连续变形可以变为球面的多面体。

欧拉定理：
定理简单多面体的顶点数V、面数F及棱数E间有关系V+F-E=2;
公式描述了简单多面体中顶点数、面数、棱数之间特有的规律。

定理的证明：
分析：以四面体ABCD为例.
将它的一个面BCD去掉,再使它变为平面图形，四面体的顶点数V、棱数E 与剩下的面数F1变形后都没有变（这里F1=F-1）。

因此，要研究V、E 和F的关系,只要去掉一个面,将它变形为平面图形即可。

只需平面图形证明：V+F1-E=1；
(1)去掉一条棱,就减少一个面，V+F1-E的值不变。

例如去掉BC，就减少一个面ABC。

同理，去掉棱CD、BD,也就各减少一个面ACD、ABD，由于V、F1—E的值都不变,因此V+F1-E的值不变；
(2)再从剩下的树枝形中,去掉一条棱，就减少一个顶点,V+F1-E的值不变.例如去掉CA，就减少一个顶点C.同理去AD就减少一个顶点D，最后剩下AB.
在以上变化过程中，V+F1—E的值不变,V+F1-E=2—0—1=1,所以 V+F—E= V+F1-E+1=2。

对任意的简单多面体，运用这样的方法,都是只剩下一条线段。

公式对任意简单多面体都是正确的。

欧拉定理又一证法：
多面体，设顶点数V,面数F,棱数E。

剪掉一个面，将其余的面拉平，使它变为平面图形, 我们在两个图中求所有面的内角总和Σα。

一方面，利用面求内角总和.。

空间中的欧拉公式V+F-E=X(P)，V是多面体P的顶点个数，F是多面体P的面数，E是多面体P的棱的条数,X(P)是多面体P的欧拉示性数。

如果P可以同胚于一个球面（可以通俗地理解为能吹胀而绷在一个球面上），那么X(P)=2，如果P同胚于一个接有h个环柄的球面，那么X(P)=2-2h。

X(P)叫做P的欧拉示性数，是拓扑不变量，就是无论再怎么经过拓扑变形也不会改变的量，是拓扑学研究的范围。

在多面体中的运用:简单多面体的顶点数V、面数F及棱数E间有关系V+F-E=2这个公式叫欧拉公式。

公式描述了简单多面体顶点数、面数、棱数特有的规律。

平面上的欧拉公式V+F-E=X(P),其中V是图形P的顶点个数，F是图形P内的区域数，E是图形的边数。

在非简单多面体中，欧位公式的形式为：V-E+F-H=2(C-G)其中H指的是平面上不完整的个数，而C指的是独立的多面体的个数，G指的是多面体被贯穿的个数。

证明（1）把多面体（图中①）看成表面是薄橡皮的中空立体。

（2）去掉多面体的一个面，就可以完全拉开铺在平面上而得到一个平面中的直线形，像图中②的样子。

假设F′，E′和V′分别表示这个平面图形的（简单）多边形、边和顶点的个数，我们只须证明F′-E′+V′=1。

（3）对于这个平面图形，进行三角形分割，也就是说，对于还不是三角形的多边形陆续引进对角线，一直到成为一些三角形为止，像图中③的样子。

每引进一条对角线，F′和E′各增加1，而V′却不变，所以F′-E′+V′不变。

因此当完全分割成三角形的时候，F′-E′+V′的值仍然没有变。

有些三角形有一边或两边在平面图形的边界上。

（4）如果某一个三角形有一边在边界上，例如图④中的△ABC，去掉这个三角形的不属于其他三角形的边，即AC，这样也就去掉了△ABC。

这样F′和E′各减去1而V′不变，所以F′-E′+V′也没有变。

（5）如果某一个三角形有二边在边界上，例如图⑤中的△DEF，去掉这个三角形的不属于其他三角形的边，即DF和EF，这样就去掉△DEF。