下载文档原格式
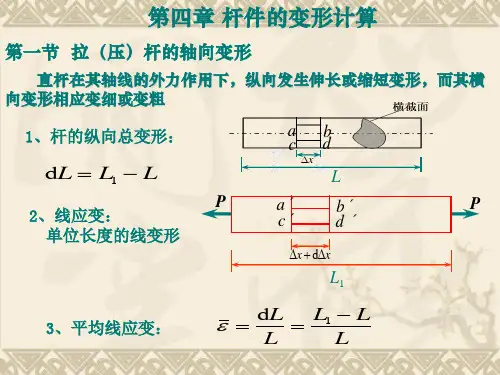
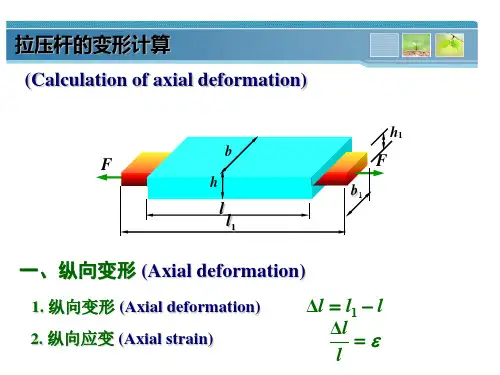
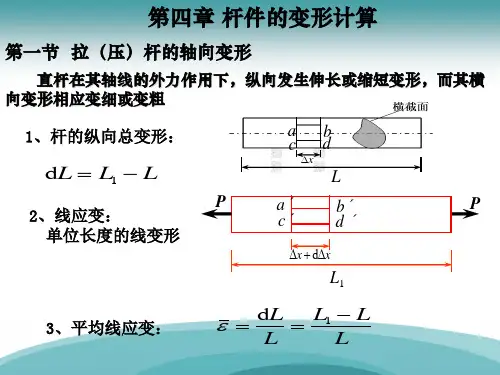
§2-5拉伸或压缩时的变形1．沿杆件轴线的轴向变形如图2-23，设等直杆的原长为，横截面面积为。
在轴向力l A P 作用下，长度由l 变为。
杆件在轴线方向的伸长，即轴向变形为1ll l l −=Δ1 （1）由于杆内各点轴向应力σ与轴向应变ε为均匀分布，所以一点轴向线应变即为杆件的伸长除以原长l ：l Δl l Δ=ε （2） 由εσE =得ll E A N Δ= 所以EAPl EA Nl l ==Δ （2-6） 式（2-6）表示：当应力不超过比例极限时，杆件的伸长l Δ与拉力P 和杆件的原长度l 成正比，与横截面面积成反比。
这是胡克定律的另一种表达形式。
式中是材料弹性模量与拉压杆件横截面面积乘积，EA 越大，则变形越小，将EA 称为抗拉（压）刚度。
A EA 2．横向变形若在图2-23中，设变形前杆件的横向尺寸为，变形后相应尺寸变为，则横向变形为 b 1bb b b −=Δ1横向线应变可定义为bb Δ=′ε 由实验证明，在弹性范围内μεε=′ （2-7） μ为杆的横向线应变与轴向线应变代数值之比。
由于μ为反映材料横向变形能力的材料弹性常数，为正值，所以，一般冠以负号εεμ′−=，称为泊松比或横向变形系数。
ε′与ε的关系为μεε−=′ （2-8）3()()x Nx e σγ0 ()A dA A σσγ+=+在处0=x 0A A =即：按指数函数变化。
A 例2-6 图2-25所示为变截面杆，已知BD 段cm 21=A 2，DA 段42=A cm 2，kN ，kN 。
求AB 杆的变形5=AB l 1P 102=P Δ。
（材料的MPa ）310120×=E 解：首先分别求得BD 、DC 、CA 三段的轴力，N ，为1N 23N 51−=N kN ；52−=N kN ；53=N kN449311111005.1102101205.0105−−×−=×××××−==Δ=ΔEA l N l l BD （m ） 449322221052.0104101205.0105−−×−=×××××−==Δ=ΔEA l N l l DC （m ） 449333331052.0104101205.0105−−×=×××××==Δ=ΔEA l N l l CA（m ） 43211005.1−×−=Δ+Δ+Δ=Δl l l l AB （m ） AB l Δ的负号说明此杆缩短。
杆的变形量计算公式
杆件弯曲变形量可以通过杆件的杨氏模量、截面形状、杆件受力状态来计算。
下面是一般情况下杆的变形量计算公式：
1.直杆内力引起的弯曲变形量计算公式：
弯曲变形量(δ)=(M*L)/(E*I)
其中
δ为弯曲变形量
M为杆件的弯矩（Nm）
L为杆件的长度（m）
E为杆件的杨氏模量（Pa）
I为杆件的截面惯性矩（m^4）。
2.断面变形量引起的弯曲变形量计算公式：
弯曲变形量(δ)=(F*L)/(E*A)
其中
δ为弯曲变形量
F为杆件的力（N）
L为杆件的长度（m）
E为杆件的杨氏模量（Pa）
A为杆件的横截面积（m^2）。
这两个公式分别用于计算杆件在受到弯矩和受力作用下的弯曲变形量。
在实际应用中，根据杆件的不同形状和受力情况，可以选择相应的公式进
行计算。
此外，如果杆件的形状不规则，或杆件受力情况较为复杂，可以使用
数值方法来计算杆的变形量。
常用的数值方法包括有限元分析、杆件切割
法等。
综上所述，杆的变形量计算公式是根据杆件的弹性特性和几何形状推
导而来的。
通过这些公式，我们可以计算出杆件在受到弯矩和受力作用下
的弯曲变形量，为工程设计和结构分析提供了依据。
但在实际应用中，还
需要考虑一些特殊情况，并使用合适的数值方法进行计算。
