《材料力学》扭转习题解

第 三 章 扭 转一、判断题1．杆件受扭时，横截面上的最大切应力发生在距截面形心最远处。

（ × ） 2．薄壁圆管和空心圆管的扭转切应力公式完全一样。

（ × ） 3．圆杆扭转变形实质上是剪切变形。

（ √ ） 4．非圆截面杆不能应用圆截面杆扭转切应力公式，是因为非圆截面杆扭转时“平截面假设”不能成立。

（ √ ）5．材料相同的圆杆，它们的剪切强度条件和扭转强度条件中，许用应力的意义相同，数值相等。

（ × ） 6．切应力互等定理，仅适用于纯剪切情况。

（ × ) 7．受扭杆件的扭矩，仅与杆件受到的转矩（外力偶矩）有关，而与杆件的材料及其横截面的大小、形状无关。

( √ ) 8．受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。

（ √ ) 9．受扭圆轴的最大切应力只出现在横截面上。

（ × ) 10． 因木材沿纤维方向的抗剪能力差，故若受扭木质圆杆的轴线与木材纤维方向平行，当扭矩达到某一极限值时，圆杆将沿轴线方向出现裂纹。

（ √ )二、填空题1．一级减速箱中的齿轮直径大小不等，在满足相同的强度条件下，高速齿轮轴的直径要比低速齿轮轴的直径（ 小 ）。

2． 当实心圆轴的直径增加1培时，其抗扭强度增加到原来的（ 8 ）倍，抗扭刚度增加到原来的（ 16 ）倍。

3． 直径D=50mm 的圆轴，受扭矩T=2.15kn.m ,该圆轴横截面上距离圆心10mm 处的剪应力τ=（35.0 MPa ），最大剪应力τmax=（87.6 MPa ）。

4． 一根空心轴的内外径分别为d ，D ，当D=2d 时，其抗扭截面模量为（33256153215D d ππ或）。

5． 直径和长度均相等的两根轴，在相同的扭矩作用下，而材料不同，它们的τmax 是（ 相 ）同的，扭转角φ是（ 不 ）同的。

6． 等截面圆轴扭转时的单位长度相对扭转角为θ，若圆轴直径增大一倍，则单位长度扭转角将变为（16θ）。

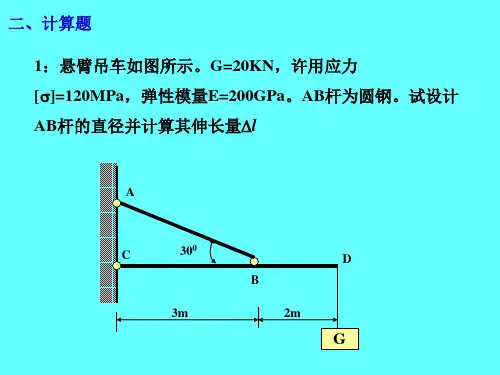
3—1 一传动轴作匀速转动，转速，轴上装有五个轮子，主动轮Ⅱ输入的功率为60kW，从动轮,Ⅰ,Ⅲ，Ⅳ，Ⅴ依次输出18kW，12kW,22kW和8kW。

试作轴的扭矩图。

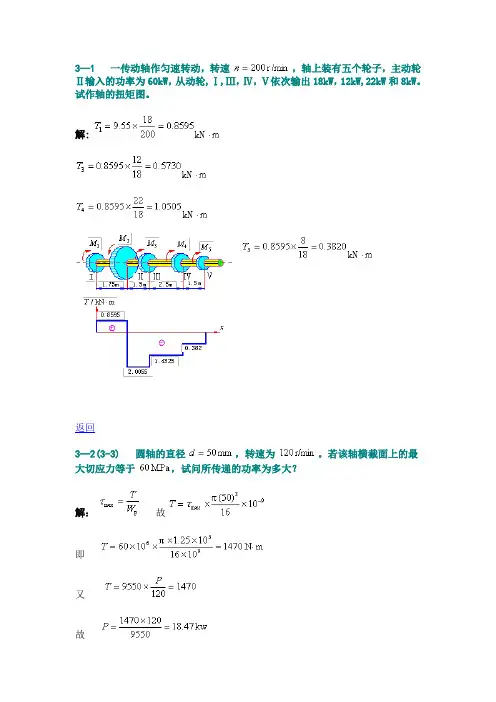
解:kNkNkNkN返回3—2(3-3)圆轴的直径，转速为。

若该轴横截面上的最大切应力等于，试问所传递的功率为多大？解：故即又故返回3—3（3—5）实心圆轴的直径mm，长m，其两端所受外力偶矩，材料的切变模量。

试求:（1)最大切应力及两端截面间的相对扭转角；（2)图示截面上A，B，C三点处切应力的数值及方向；（3）C点处的切应变。

解：=返回3-4(3—6)图示一等直圆杆，已知，，，。

试求:（1）最大切应力；（2）截面A相对于截面C的扭转角。

解：(1）由已知得扭矩图（a）(2)返回3-5(3—12)长度相等的两根受扭圆轴，一为空心圆轴，一为实心圆轴,两者材料相同,受力情况也一样。

实心轴直径为d;空心轴外径为D，内径为，且。

试求当空心轴与实心轴的最大切应力均达到材料的许用切应力），扭矩T相等时的重量比和刚度比。

解：重量比=因为即故故刚度比==返回3—6(3-15）图示等直圆杆，已知外力偶矩,，许用切应力，许可单位长度扭转角，切变模量。

试确定该轴的直径d。

解:扭矩图如图（a)(1)考虑强度，最大扭矩在BC段,且(1）(2）考虑变形（2）比较式（1）、(2），取返回3-7(3—16) 阶梯形圆杆,AE段为空心,外径D=140mm，内径d=100mm；BC段为实心，直径d=100mm。

外力偶矩，，。

已知：，,。

试校核该轴的强度和刚度。

解:扭矩图如图（a)（1)强度=，BC段强度基本满足=故强度满足。

（2）刚度BC段：BC段刚度基本满足.AE段：AE段刚度满足，显然EB段刚度也满足.返回3—8(3-17）习题3—1中所示的轴,材料为钢,其许用切应力，切变模量，许可单位长度扭转角。

试按强度及刚度条件选择圆轴的直径。

解:由3—1题得：故选用.返回3-9(3-18）一直径为d的实心圆杆如图，在承受扭转力偶矩后，测得圆杆表面与纵向线成方向上的线应变为。

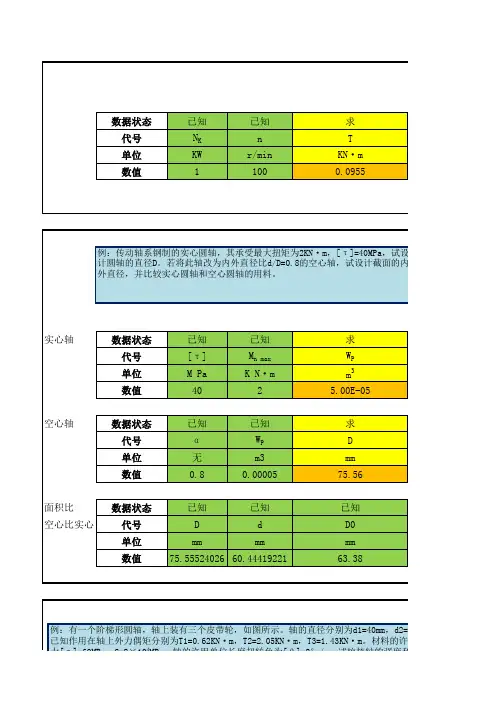
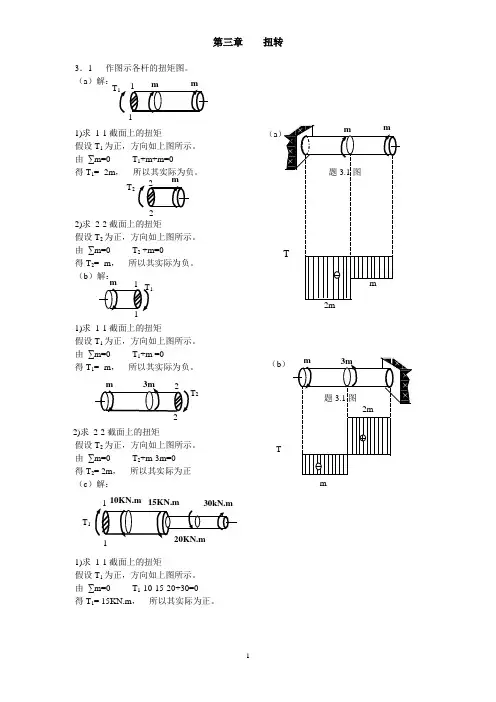
第三章 扭转3．1 作图示各杆的扭矩图。

（a ）解：1)求 1-1截面上的扭矩假设T 1为正，方向如上图所示。

由 ∑m=0 T 1+m+m=0得T 1= -2m ， 所以其实际为负。

2)求 2-2截面上的扭矩假设T 2为正，方向如上图所示。

由 ∑m=0 T 2 +m=0得T 2= -m ， 所以其实际为负。

（b ）解：1)求 1-1截面上的扭矩假设T 1为正，方向如上图所示。

由 ∑m=0 T 1+m =0得T 1= -m ， 所以其实际为负。

2)求 2-2截面上的扭矩假设T 2为正，方向如上图所示。

由 ∑m=0 T 2+m-3m=0 得T 2= 2m ， 所以其实际为正 （c ）解：1)求 1-1截面上的扭矩假设T 1为正，方向如上图所示。

由 ∑m=0 T 1-10-15-20+30=0得T 1= 15KN.m ， 所以其实际为正。

T 1T 2（a2（b ）mTT 12)求 2-2截面上的扭矩假设T 2为正，方向如上图所示。

由 ∑m=0 T 2-15-20+30=0得T 2= 5KN.m ， 所以其实际为正。

3)求 3-3截面上的扭矩 假设T 3为正，方向如上图所示。

由 ∑m=0 T 3-20+30=0得T 3= -10KN.m ， 所以其实际为负。

4)求 4-4截面上的扭矩假设T 4为正，方向如上图所示。

由 ∑m=0 T 4 +30=0得T 4= -30KN.m ， 所以其实际为负。

3.2 T 为圆杆横截面上的扭矩，试画出截面上与T 对应的剪应力分布图。

解：3.5 D=50mm 直径的圆轴，受到扭矩T=2.15KN .m 的作用。

试求在距离轴心10mm 处的剪应力，并求轴横截面上的最大剪应力。

T 230kN.m T 3T 4（题3.2图（a ） （b ）解：求距离轴心10mm 处的剪应力， 由 I P =πD 4/32=π×0.054/32=6.13×10-7 m 4 W t = I P /R=6.13×10-7/0.025=2.454×10-5 m 3τρ=Tρ/ I P =2.15×103×10×10-3/(6.13 ×10-7 ) =35MPa求轴横截面上的最大剪应力τmax =T/ W t =2.15×103/(2.454 ×10-5 ) =87.6MPa3.8 阶梯形圆轴直径分别为d 1=40mm ，d 2=70mm ，轴上装有三个皮带轮，如图所示。

第三章 扭 转一、判断题1．圆杆受扭时，杆内各点均处于纯剪切状态。

（ ） 2．非圆截面杆不能应用圆杆扭转切应力公式，是因为非圆截面杆扭转时“平面假设”不能成立。

（ ） 3．当剪应力超过材料的剪切比例极限时，剪应力互等定律亦成立。

（ ） 4．一点处两个相交面上的剪应力大小相等，方向指向（或背离）该两个面的交线。

（ ） 5．直径和长度相同，材料不同的两根轴，受相同的扭转力偶矩作用，它们的最大剪应力和最大扭转角都相同。

6. 杆件受扭时，横截面上最大切应力发生在距截面形心最远处。

（ ）7. 薄壁圆管和空心圆管的扭转切应力公式完全一样。

（ ）8. 圆杆扭转变形实质上是剪切变形。

（ ）9. 横截面的角点处的切应力必为零。

（ ） 1.√ 2.√ 3.√ 4.× 5.× 6.×（非圆截面） 7.× 8.√ 9.× 二、单项选择题1. 图示圆轴曲面C 左、右两侧的扭矩MC+和M C-的（ ）。

A ．大小相等，正负号相同；B ．大小不等，正负号相同； C ．大小不等，正负号不同；D ．大小相等，正负号不同。

2. 直径为D 的实心圆轴，两端受扭转力矩作用。

轴内最大剪应力τ，若轴的直径改为D/2，则轴内的最大剪应力变为（ ）。

A ．2τ； B ．τ； C ． 8τ； D ．16τ。

3. 阶梯圆轴的最大切应力发生在（ ）。

A ．扭矩最大的截面；B ．直径最小的截面；C ．单位长度扭转角最大的截面；D ．不能确定。

4.空心圆轴的外径为D ，内径为d,α=d/D 。

其抗扭截面系数为（ ）。

A ．()απ-=1163D W P ；B 。

()23116απ-=D W P ；C 。

()33116απ-=D W PD ．()43116απ-=D WP5.扭转的切应力公式ρτρPPI M =适用于（ ）杆件。

A ．任意截面； B ．任意实心截面；C ．任意材料的圆截面； D ．线弹性材料的圆面。

扭 转1. 一直径为1D 的实心轴，另一内径为d , 外径为D , 内外径之比为22d D α=的空心轴，若两轴横截面上的扭矩和最大切应力均分别相等，则两轴的横截面面积之比12/A A 有四种答案：(A) 21α-； (B)(C)； (D)。

2. 圆轴扭转时满足平衡条件，但切应力超过比例极限，有下述四种结论： (A) (B) (C) (D) 切应力互等定理： 成立 不成立 不成立 成立 剪切胡克定律： 成立 不成立 成立 不成立3. 一内外径之比为/d D α=的空心圆轴，当两端承受扭转力偶时，若横截面上的最大切应力为τ，则内圆周处的切应力有四种答案：(A) τ ； (B) ατ； (C) 3(1)ατ-； (D) 4(1)ατ-。

4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。

扭转时，表面的纵向线倾斜了γ角，在小变形情况下，此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案：7. 图示圆轴料的切变模量(A) 43π128d G a ϕ(C) 43π32d G a ϕ8. 一直径为D重量比21W W 9. 想弹塑性材料， 等直圆轴的极限扭矩是刚开始出现塑性变形时扭矩的 倍。

10. 矩形截面杆扭转变形的主要特征是 。

1-10题答案：1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.479. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩；4/3 10. 横截面翘曲11. 已知一理想弹塑性材料的圆轴半径为R ，扭转加载到整个截面全部屈服，将扭矩卸掉所产生的残余应力如图所示，试证明图示残余应力所构成的扭矩为零。

证：截面切应力 4103s R R ρρττρ⎛⎫=-≤≤ ⎪⎝⎭截面扭矩 04d 12πd 03Rs s A T A R ρρτρτρρ⎛⎫==-⋅= ⎪⎝⎭⎰⎰ 证毕。

12. 图示直径为d 的实心圆轴,两端受扭转力偶e M 用1/m C τγ=表示，式中C ，m 为由实验测定的已知常数，试证明该轴的扭转切应力计算公式为：1/e (31)/2π()23m 1mm mM m d ρρτ+=+s /3证：几何方面 d d xρϕγρ= 物理方面 1/1/d d mmC C x ρϕτγρ⎛⎫== ⎪⎝⎭静力方面 1//21/e 0d d 2πd d md mAM T A C x ρϕρτρρρρ⎛⎫==⋅⋅=⋅⋅ ⎪⎝⎭⎰⎰1//221/0d 2πd d m d mC x ϕρρ+⎛⎫= ⎪⎝⎭⎰(31)/1/()d 22π(31)d m mmd C m x mϕ+⎛⎫= ⎪+⎝⎭1/e (31)/(31)d d 2π()2mm m M m d x Cm ϕ++⋅⎛⎫=⎪⎝⎭⋅ 所以 1/e (31)/2π()23m 1mm mM m d ρρτ+=+ 证毕。

电气工程师-公共基础-材料力学-扭转[单选题]1.已知实心圆轴按强度条件可承担的最大扭矩为T，若改变该轴的直径，使其横截面积增加1倍。

则可承担的最大扭矩为()。

[2019年真（江南博哥）题]A.B.2TC.D.4T正确答案：C参考解析：扭转剪应力公式为：。

式中，Wp为抗扭截面系数，且。

当横截面面积增加一倍时，直径变为原来的倍。

根据扭转剪应力公式，当最大剪应力不变时，直径变为原来的倍时，可承受的最大扭矩为。

[单选题]2.圆轴直径为d，剪切弹性模量为G，在外力作用下发生扭转变形，现测得单位长度扭转角为θ，圆轴的最大切应力是()。

[2013、2010年真题]A.τ＝（16θG）/（πd3）B.τ＝（θGπd3）/16C.τ＝θGdD.τ＝θGd/2正确答案：D参考解析：由公式θ＝T/（GIp）得：T＝θGIp。

其中，Ip＝（d/2）·Wp。

则最大切应力τ＝T/Wp＝GθIp/Wp＝θGd/2。

[单选题]3.在一套传动系统中，有多根圆轴，假设所有圆轴传递的功率相同，转速不同。

该系统的圆轴转速与其扭矩的关系是()。

[2016、2014年真题]A.转速快的轴扭矩大B.转速慢的轴扭矩大C.全部轴的扭矩相同D.无法确定正确答案：B参考解析：根据公式T＝9550P/n可知，在功率相同的情况下转速慢的轴扭矩大。

式中，T为扭矩（N·m）；P为功率（kW）；n为转速（r/min）；9550为常系数。

[单选题]4.图5-3-1所示两根圆轴，横截面面积相同，但分别为实心圆和空心圆。

在相同的扭矩T作用下，两轴最大切应力的关系是()。

[2013年真题]图5-3-1A.τa＜τbB.τa＝τbC.τa＞τbD.不能确定正确答案：C参考解析：设d1为实心圆直径，D2为空心圆截面外径，d2为空心圆截面内径，α2＝d2/D2。

由最大切应力公式τmax＝T/WP，由两轴截面面积相等得：πd12/4＝πD22（1－α22）/4，即：实心圆截面的抗扭截面系数WPa＝πd13/16；空心圆截面的WPb＝πD23（1－α24）/16，因此两轴的抗扭截面系数之比为：故τa＞τb。

19-1 19-2 19-3 19-5 19-4、19-8 19-1019-1 绘制图示各杆的扭矩图。

参考答案略19-2 直径为D =5cm 的圆轴，受到扭矩n M =2.15kN ·m 的作用，试求在距离轴心1cm 处的剪应力，并求轴截面上的最大剪应力。

参考答案：由圆轴扭转横截面上任意一点剪应力计算公式可知，距轴心1cm 处的剪应力为MPa I M pn 353250101015.246=⨯⨯⨯==πρτρ截面上的最大剪应力：MPa W M tn 6.8716501015.236max =⨯⨯==πτ 19-3 已知作用在变截面钢轴上的外力偶矩1m =1.8kN ·m ，2m =1.2kN ·m 。

试求最大剪应力和最大相对转角。

材料的G =80GPa 。

参考答案：直径为75mm 段的扭矩为m KN m m T .3)(211-=+-=； 直径为50mm 段的扭矩为KNm m T 2.122-=-=。

最大剪应力计算：MPa W T t 2.3616751033611max 1=⨯⨯==πτ；MPa W T t 9.481650102.13622max 2=⨯⨯==πτ则最大剪应力MPa 9.48max =τ最大相对转角计算：22.10212773.0102231.121005416.932501080500102.13275108075010333436436222111max 2max 1max ==⨯+⨯=⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯=+=+=--rad rad rad GI lT GI l T P P ππϕϕϕ 19-4 已知圆轴的转速n =300r /min ，传递功率330.75kW ，材料的][τ=60MPa ，G =82GPa 。

要求在2m 长度内的相对扭转角不超过1º，试求该轴的直径。

参考答案：计算外力偶矩（即扭矩）：m N n N Me T ⋅=⨯===875.1052830075.33095509550按强度条件设计轴的直径：[]MPa d W T t601610875.1052833max =≤⨯==τπτ mm d 32.966010875.105281633=⨯⨯≥π按刚度条件设计轴的直径：118032108210210875.105281804333max ≤⨯⎪⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯=⨯=πππϕd GI Tl p 得 mm d 64.110108232180********.1052842333=⨯⨯⨯⨯⨯⨯⨯≥π故该轴的直径mm d 64.110≥19-5 图示一圆截面直径为80cm 的传动轴，上面作用的外力偶矩为1m =1000N ·m ，2m =600N ·m ，3m =200N ·m ，4m =200N ·m ，（1）试作出此轴的扭矩图，（2）试计算各段轴内的最大剪应力及此轴的总扭转角（已知材料的剪切弹性模量G =79GPa ）；（3）若将外力偶矩1m 和2m 的作用位置互换一下，问圆轴的直径是否可以减少？注意：此题传动轴直径应为80mm 。

材料力学第三章答案【篇一：材料力学习题册答案-第3章扭转】是非判断题二、选择题0 b 2t?d316?1?? ? b wp??d316?1?? ?2c wp??d316?1?? ? d w3p??d316?1?? ?46.对于受扭的圆轴，关于如下结论：①最大剪应力只出现在横截面上；②在横截面上和包含杆件的纵向截面上均无正应力；③圆轴内最大拉应力的值和最大剪应力的值相等。

现有四种答案，正确的是（ a ）a ②③对 b①③对 c①②对d 全对 7.扭转切应力公式?mnp?i?适用于（ d）杆件。

pa 任意杆件；b 任意实心杆件；c 任意材料的圆截面；d 线弹性材料的圆截面。

9.若将受扭实心圆轴的直径增加一倍，则其刚度是原来的（ d a 2倍； b 4倍； c 8倍； d 16倍。

三、计算题1.试用截面法求出图示圆轴各段内的扭矩t，并作扭矩图2.图示圆轴上作用有四个外力偶矩 me1 =1kn/m, me2 =0.6kn/m,）me3= me4 =0.2kn/m, ⑴试画出该轴的扭矩图；⑵若 me1与me2的作用位置互换，扭矩图有何变化？(1)(2)解： me1与me2的作用位置互换后，最大扭矩变小。

3.如图所示的空心圆轴，外径d=100㎜，内径d=80㎜，m=6kn/m,m=4kn/m.请绘出轴的扭矩图，并求出最大剪应力解：扭矩图如上，则轴面极惯性矩id4?d4)(1004?804)(10?3)4p=?(32??32?5.8?10?6m4㎜，l=500tr4?103?50?103ip5.8?104．图示圆形截面轴的抗扭刚度为g ip，每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。

ab+ad=cdab=t1l?90?gipgipad=bc=t2l100gipgipcd=t3l40gipgip?90?100?4050?gipgip【篇二：《材料力学》第3章扭转习题解】[习题3-1] 一传动轴作匀速转动，转速n?200r/min，轴上装有五个轮子，主动轮ii输入的功率为60kw，从动轮，i，iii，iv，v依次输出18kw，12kw，22kw和8kw。

材料力学扭转6.1扭转的概念扭转是杆件变形的一种基本形式。

在工程实际中以扭转为主要变形的杆件也是比较多的，例如图6-1所示汽车方向盘的操纵杆，两端分别受到驾驶员作用于方向盘上的外力偶和转向器的反力偶的作用；图6-2所示为水轮机与发电机的连接主轴，两端分别受到由水作用于叶片的主动力偶和发电机的反力偶的作用；图6-3所示为机器中的传动轴，它也同样受主动力偶和反力偶的作用，使轴发生扭转变形。

图6—1图6—2图6—3这些实例的共同特点是：在杆件的两端作用两个大小相等、方向相反、且作用平面与杆件轴线垂直的力偶，使杆件的任意两个截面都发生绕杆件轴线的相对转动。

这种形式的变形称为扭转变形（见图6-4）。

以扭转变形为主的直杆件称为轴。

若杆件的截面为圆形的轴称为圆轴。

图6—46.2扭矩和扭矩图6.2.1外力偶矩作用在轴上的外力偶矩，可以通过将外力向轴线简化得到，但是，在多数情况下，则是通过轴所传递的功率和轴的转速求得。

它们的关系式为nP M 9550=（6-1） 其中：M ——外力偶矩（N ·m ）;P ——轴所传递的功率（KW ）； n ——轴的转速（r ／min ）。

外力偶的方向可根据下列原则确定：输入的力偶矩若为主动力矩则与轴的转动方向相同；输入的力偶矩若为被动力矩则与轴的转动方向相反。

6.2.2扭矩圆轴在外力偶的作用下，其横截面上将产生连续分布内力。

根据截面法，这一分布内力应组成一作用在横截面内的合力偶，从而与作用在垂直于轴线平面内的外力偶相平衡。

由分布内力组成的合力偶的力偶矩，称为扭矩，用n M 表示。

扭矩的量纲和外力偶矩的量纲相同，均为N·m 或kN·m 。

当作用在轴上的外力偶矩确定之后，应用截面法可以很方便地求得轴上的各横截面内的扭矩。

如图6-5（a ）所示的杆，在其两端有一对大小相等、转向相反，其矩为M 的外力偶作用。

为求杆任一截面m-m 的扭矩，可假想地将杆沿截面m-m 切开分成两段，考察其中任一部分的平衡，例如图6-5（b ）中所示的左端。