当前位置：文档之家 › 材料力学基本第五章 圆轴扭转

材料力学基本第五章 圆轴扭转

  • 格式：ppt
  • 大小：2.03 MB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

材料力学 第五章扭转变形.强度、刚度条件(6,7,8)汇总

材料力学 第五章扭转变形.强度、刚度条件(6,7,8)汇总

Me Tb Ta
( 4)
例题 6-6
5. 实心铜杆横截面上任意点的切应力为 Ta Ga M e 0 ra ρa I pa Ga I pa Gb I pb 空心钢杆横截面上任意 点的切应力为
b
Tb Gb M e I pb Ga I pa Gb I pb
2
1 dV (dxdydz ) 2 dV dW v dV dxdydz 1 v 2





一、密圈螺旋弹簧
——螺旋角
F
O

d
d ——簧丝横截面的直径 D ——弹簧圈的平均直径
O D
密圈螺旋弹簧 ——螺旋角<5°时的圆柱形弹簧
§4.5
密圈螺旋弹簧的计算
O F
例题 6-6
Me Tb Ta
解： 1. 实心铜杆和空心钢杆横截面上的扭矩分别为Ta 和Tb(图b)，但只有一个独立平衡方程 Ta+Tb= Me (1) 故为一次超静定问题。
例题 6-6
Me Tb Ta
2. 位移相容条件为实心杆和空心杆的B截面相对 于A截面的扭转角相等。在图b中都用表示（设 A端固定）。 Ba Bb ( 2)
a
b
ra
ra
a rb
切应力沿半径的变化 情况如图c所示。
ra
rb
(c)
§5-8非圆截面等直杆扭转的概念
圆截面杆扭转时的应力和变形公式,均建立在平 面假设 的基础上。对于非圆截面杆,受扭时横截面不 再保持为平面，杆的横截面已由原来的平面变成了曲 面。这一现象称为截面翘曲。因此,圆轴扭转时的应 力、变形公式对非圆截面杆均不适用。
(2)
材料力学 扭转

材料力学 扭转

在相互垂直的两 个平面上，切应力必 然成对存在，且数值 相等；两者都垂直于 两个平面的交线，方 向则共同指向或共同 背离这一交线。
各个截面上只有切应力没 有正应力的情况称为纯剪切 纯剪切
§3.3 纯剪切
三、切应变 剪切胡克定律
在切应力的作用下，单元 体的直角将发生微小的改变， 这个改变量 称为切应变。
（1）校核强度
max
Tmax Wt
Tmax
（2）设计截面
Wt

（3）确定载荷
Tmax Wt
§3.4 圆轴扭转时的应力
例3.2 由无缝钢管制成的汽车传动轴，外径D=90mm，壁厚 =2.5mm，材料为20号钢，使用时的最大扭矩T=1930N· m， []=70MPa。校核此轴的强度。 解：（1）计算抗扭截面模量 d 0.944 D Wt 0.2 D3 (1 4 ) 0.2 9.03 (1 0.9444 ) 30 cm3 （2） 强度校核
材料力学
龚峰
gongfeng@
第3章
扭转
§3.1 扭转的概念和实例 §3.2 外力偶矩的计算 扭矩和扭矩图 §3.3 纯剪切 §3.4 圆轴扭转时的应力 §3.5 圆轴扭转时的变形 §3.6 扭转静不定问题
§3.7
非圆截面杆扭转的概念
§3.1 扭转的概念和实例
汽车方向盘
§3.1 扭转的概念和实例
§3.2 外力偶矩的计算 扭矩和扭矩图
M A (9549 45) / 300 1432 (N· m) m) M B (954910) / 300 318 (N· m) M C (954915) / 300 477 (N· m) M D (9549 20) / 300 637 (N·
材料力学-扭转1ppt课件

材料力学-扭转1ppt课件


横截面上 —
max
T IP
max
IP
T
max
T WP
Ip—截面的极惯性矩，单位：m4 , mm 4
WP
Ip
max
WP —抗扭截面模量，单位：m3, mm3.
整个圆轴上——等直杆：
max
Tm a x WP
三、公式的使用条件： 1、等直的圆轴， 2、弹性范围内工作。
30
四、圆截面的极惯性矩 Ip 和抗扭截面系数Wp
d
dx
d / dx－扭转角变化率
二）物理关系：
弹性范围内 max P
G → G
G
d
dx
方向垂直于半径。
28
三）静力关系：
T A dA
T A dA
G d 2dA dx A
I p
2dA
A
Ip
横截面对形心的极惯性矩
T
GI p
d
dxp
29
二、圆轴中τmax的确定
结论：
横截面上 0, 0 0 0
根据对称性可知剪应力沿圆周均匀分布；
t D, 可认为剪应力沿壁厚均匀分布,
且方向垂直于其半径方向。
t
D
20
3、剪应力的计算公式：
T
AdA.r0
2 0
r0
2td
r02t2
d
T
2r0 2t
薄壁圆筒横截面上的剪应力计算式
21
二、关于剪应力的若干重要性质
例题： 1、一传动轴作200r／min的匀速转动，轴上装有五个轮子。 主动轮2输入的功率为60kW，从动轮1、3、4、5依次输出的 功率为18kW、12kW、22kW和8kW。试作出该轴的扭矩图。
材料力学-扭转

材料力学-扭转


扭转角（ 扭转角（ϕ）：任意两截面绕轴线相对转动的角度。又称为角 位移。通常用ϕ表示。ϕB − A表示B截面相对A截面转过的角度。 剪应变（ 剪应变（γ）： 剪应变又叫角应变或切应变，它是两个相互垂直方 向上的微小线段在变形后夹角的改变量（以弧度表示， 角度减小时为正） O ϕ B m
A m
γ
第二节 杆受扭时的内力计算
四、圆截面的极惯性矩 Ip 和抗扭截面系数Wp
实心圆截面： 实心圆截面：
2
I p = ∫ ρ d A = ∫ ρ (2 πρ d ρ )
2
ρ
d O
dρ
A
d 2 0
= 2 π(
ρ
4
d /2
4
)
0
πd = 32
4
d A = 2 πρ d ρ
πd 3 Wp = = d / 2 16 Ip
空心圆截面： 空心圆截面：
T T = ρ max = IP IP T = WP
ρ max
Ip—截面的极惯性矩， 截面的极惯性矩，单位： 单位：m 4 , mm 4 Ip 3 3 WP —抗扭截面模量， WP = 抗扭截面模量，单位：m , mm .
ρ max
整个圆轴上——等直杆： 等直杆： τ max
Tmax = WP
三、公式的使用条件： 公式的使用条件： 1、等直的圆轴， 等直的圆轴， 2、弹性范围内工作。 弹性范围内工作。
Tmax Wp
πD 3 实心, 16 T max W = 2）设计截面尺寸: 设计截面尺寸:WP ≥ 3 P [τ ] πD (1 − α 4 ) 空心. 16 ≤ ⇒ m 3）确定外荷载: 确定外荷载: Tmax WP ⋅ [τ ]
≤
高教版材料力学扭转刘鸿文2011

高教版材料力学扭转刘鸿文2011


dx
b
d
是 b-b 截面相对于

a—a 截面象刚性平面一 样绕杆 轴转动的一个角度。
(a)
a


GG' d tan dx EG

d dx
(a)
b
T
T
O
2

O
1
E
G
D
A

'

'
a
此时式说明 ： 同一 半径 圆周变 均相同 ，且其值与
得到
τ
Τ 2 Α0 t
γ
r
l
薄壁圆筒切应力计算公式推倒过程
τ
Τ 2 Α0 t
薄壁圆筒切应 力计算公式
γ
r
l
薄壁圆筒切应 变计算公式
二、切应力互等定理 y
dz
单元体：微小的正六面体
在扭转时，左右两侧面（杆的横截 面）上只有切应力，方向与y轴平行， 前后无应力。
′
o

dy
x
dx
m T
•
x
m
•
T
•
x
例题3-1 传动轴如图所示，其转速 n = 300r/min ，主动轮输入 的功率为有 PA = 36 kW 。若不计轴承摩擦所耗的功率，三个 从动轮输出的功率分别为 PB =PC = 11 kW及PD = 14 kW。试画 出轴的扭矩图。 PA PB PC PD 解:计算外力偶矩 n PA meA 9550 n A B C D m4 m3 m1A m2 1146 N m
由平衡知：τ′=τ
z
切应力互等定理：两个 相互垂直平面上的剪应力τ和τ′数值
材料力学—— 扭转[学习内容]

材料力学—— 扭转[学习内容]


m)
MB
9549
PB n
63.7(N m)
n=300r/min
MC 95.5(N m),
M D 159 .2(N m),
B
C
A
D
2、求内力 M B
MB
T3 B
MC
MD
I C
I
T1 M B 0
T1
T1 M B 63.7( N m )
T2 M B MC 0
T2
T2 M B MC 159.2( N m )
求（1）轴的最大切应力；
（2）截面B和截面C的扭转角；
（3）若要求BC段的单位扭转角与AB段的相等，则在BC段
钻孔的孔径d´应为多大？
M1
M2
AB L
C L
M1
M 2 d=90mm ,L=50cm, ，G=80GPa,
M1 8KN.m
M 2 3KN .m
AB L
T 5KN.m
C L
B
C
A
3KN.m
M1＝600Nm M2=200Nm
d=40
d=30
4、n=80r/min，轴的许用剪应力[τ]＝60MPａ， 设计实心轴的直径。
PB=20KW
PA
PC=40KW
5、已知轴传递的功率，如果二段轴内的最大 剪应力相等，求二段轴的直径之比。
PB=200KW
300KW
PC=500KW
6、圆轴的外经为D＝90毫米，壁厚为ｔ＝2.5毫米。 承受的内径为T＝1500Nｍ。轴的许用应力为[τ]＝ 60MP，校核强度。
工程上采用空心截面构件：提高强度，节约材料，重量轻， 结构轻便，应用广泛。
圆轴扭转时的破坏
圆轴扭转时的破坏
16-17 材料力学 扭转详解

16-17 材料力学 扭转详解

换位后轴的扭矩如图所示此时轴的最大直径才421knm281487888990横截面相等的两根圆轴一根为实心许用剪应力为另一根为空心内外直径比若仅从强度条件考虑哪一根圆轴能承受较大的扭矩
1
扭转
圆轴扭转时的应力分析
1. 扭转的概念 4种基本变形（轴向拉压、剪切、扭转、弯曲）之一
特点：
圆截面轴（实心、空心）
17
18
19
20
一、传动轴的外力偶矩
传递轴的传递功率、转速与外力偶矩的关系：
m 9549 Pk (N m) n
9.55 Pk (kN m) n
m 7024 PPS (N m) n
7.024 PPS (kN m) n
其中：P — 功率，千瓦（kW） n — 转速，转/分（rpm）
—该点到圆心的距离。
Ip—截面极惯性矩，纯几何量，无物理意义。
48
IP A 2dA
单位：mm4，m4。
③ 尽管由实心圆截面杆推出，但同样适用于空心圆截面杆，
只是IP值不同。
a. 对于实心圆截面：
IP A 2dA
D
2 2 2 d 0
d
O
D
24
D 2
D4
4
0 32
49
b. 对于空心圆截面：
应变分布规律 应力分布规律 应力计算公式
物理方面
静力学方面
38
二、等直圆杆扭转时横截面上的应力：
1. 变形几何关系：
tg
G1G dx
d
dx
d
dx
距圆心为 任一点处的与该点到圆心的距离成正比。
d
dx
—— 扭转角沿长度方向变化率。
39
tg
G1G dx
材料力学 圆轴扭转内力、应力

材料力学 圆轴扭转内力、应力

dx GIP


T
IP
27
§ 3.4 圆轴扭转时横截面上的应力
Mechanic of Materials


T
Ip
—横截面上距圆心为处任一点切应力计算公式。
4. 公式讨论：
① 仅适用于各向同性、线 弹性材料，在小变形时的 等圆截面直杆。
τ

O
② 式中： —该点到圆心的距离。
T—横截面上的扭矩，由截面法通过外力偶矩求得。 IP—极惯性矩，纯几何量，无物理意义。
重点：扭转内力、应力。 难点：切应力互等定理的证明。 学时安排：2
Mechanic of Materials
第八讲内容目录 第三章 扭 转
§ 3.1 扭转的概念和实例和实例 § 3.2 外力偶的计算 扭矩与扭矩图 § 3.3 纯剪切 § 3.4 圆轴扭转时横截面上的应力
目录
§ 3.1 扭转的概念和实例
§3-4 圆轴扭转时横截面上的应力
约为80GPa。
剪切弹性模量、弹性模量和泊松比是表明材料弹性性质的三
个常数。对各向同性材料，这三个弹性常数之间存在下列关系：
G

E 2(1
)
22
Mechanic of Materials
§ 3.4 圆轴扭转时横截面上的应力
一、圆轴扭转时横截面上的应力公式推导思路 （一）几何方面：
扭转时，圆轴的表面 变形和薄壁圆筒表面变形 相似。实验现象：
M
A

9549
36 300
1146N.m
MB

MC

9549
11 300

350N.m
MD

9549
材料力学(第五版)扭转切应力

材料力学(第五版)扭转切应力


(
)
d 2 = 0.8D2=43 mm π 2 d1 A1 452 4 = = =1.95 2 2 A2 π D2 1 α2 53.7 1 0.8 2 4
(
)
(
)
空心圆轴能比实心圆轴更充分的使用材料。 空心圆轴能比实心圆轴更充分的使用材料。
理由？ 理由？
空心圆轴能比实心圆轴更充分的使用材料的原因： 空心圆轴能比实心圆轴更充分的使用材料的原因：
(
)
五、圆轴扭转时的强度条件 圆轴扭转时的最大切应力不能超过 材料的许用切应力
τmax
T ax m = ≤ [τ] W p
例题 d2
A
B
C
d1 mA mB mC
已知： 已知：阶梯轴尺寸如图 mA = 22 kN m, mB = 36 kN m, mC =14 kN m
[τ]= 80 MPa
d1 =120 m , d2 =100m m m
对于钢材: 对于钢材:
200 G= = 80GPa 2(1+ 0.25)
§3-4 圆轴扭转时的应力
一、变形几何条件 1、变形观察： 变形观察：
圆周线不变（大小、 圆周线不变（大小、 间距都不变） 间距都不变） 纵向线倾斜， 纵向线倾斜， 倾斜角相同 表面矩形变成 平行四边形
薄壁圆筒由于壁很薄， 薄壁圆筒由于壁很薄，表 面变形即为内部变形。 面变形即为内部变形。
圆轴内部任意一点的切应力 圆轴内部任意一点的切应力 τ ρ 与该点到圆心的距离ρ 与该点到圆心的距离ρ成正比
d τ ρ = Gρ dx
(c)
ρ =0
τρ = 0
ρ=R
τ ρ =τ max
d = GR dx
三、静力关系
材料力学扭转(共56张PPT)

材料力学扭转(共56张PPT)


例题： ：空心轴和实心轴材料相同，面积相同, α= 0.5。试比较空心轴和实心轴的强度和刚度情况。
解： 1〕确定两轴尺寸关系
面积相同 (1)校核空心轴及实心轴的强度〔不考虑键槽的影响〕；
扭转角单位：弧度〔rad〕 在B、C轮处分别负载N2=75kW，N3=75kW。
D1 d1
D d 2 2可G、I见P扭—在矩—载计抗荷算扭相1、2刚同符度的号。条规件定下和，扭空矩2心图轴绘的制重量仅为实2心轴的31% 。
1、扭转杆件的内力〔截面法〕
m
m
左段：
mx 0, T m 0
T m
右段：
m x
0,
mT 0
T m
m
Tx
T
m
x
内力偶矩——扭矩 T
2、扭矩的符号规定：按右手螺旋法那么判断。
+
T
T
-
3、内力图〔扭矩图〕
扭矩图作法：同轴力图：
例题： 1、一传动轴作200r／min的匀速转动，轴上装有五个轮子。主动轮 2输入的功率为60kW，从动轮1、3、4、5依次输出的功率为18kW、 12kW、22kW和8kW。试作出该轴的扭矩图。
二、 扭转杆的变形计算
1、扭转变形：〔相对扭转角〕
d T
dx GI P
扭转变形与内力计算式
d T dx
GIP
T dx
L GIP
1) 扭矩不变的等直轴
Tl GI p
扭转角单位：弧度〔rad〕 GIP——抗扭刚度。
2)各段扭矩为不同值的阶梯轴
Tili GI pi
3)变截面轴
T (x) dx l GI p (x)
2)、设计截面尺寸:
T
Ip
材料力学专项习题练习扭转

材料力学专项习题练习扭转

扭 转1. 一直径为1D 的实心轴，另一内径为d , 外径为D , 内外径之比为22d D α=的空心轴，若两轴横截面上的扭矩和最大切应力均分别相等，则两轴的横截面面积之比12/A A 有四种答案：(A) 21α-； (B)(C)； (D)。

2. 圆轴扭转时满足平衡条件，但切应力超过比例极限，有下述四种结论： (A) (B) (C) (D) 切应力互等定理： 成立 不成立 不成立 成立 剪切胡克定律： 成立 不成立 成立 不成立3. 一内外径之比为/d D α=的空心圆轴，当两端承受扭转力偶时，若横截面上的最大切应力为τ，则内圆周处的切应力有四种答案：(A) τ ； (B) ατ； (C) 3(1)ατ-； (D) 4(1)ατ-。

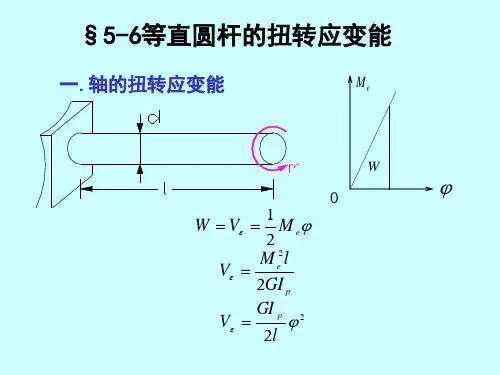
4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。

扭转时，表面的纵向线倾斜了γ角，在小变形情况下，此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案：7. 图示圆轴料的切变模量(A) 43π128d G a ϕ(C) 43π32d G a ϕ8. 一直径为D重量比21W W 9. 想弹塑性材料， 等直圆轴的极限扭矩是刚开始出现塑性变形时扭矩的 倍。

10. 矩形截面杆扭转变形的主要特征是 。

1-10题答案：1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.479. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩；4/3 10. 横截面翘曲11. 已知一理想弹塑性材料的圆轴半径为R ，扭转加载到整个截面全部屈服，将扭矩卸掉所产生的残余应力如图所示，试证明图示残余应力所构成的扭矩为零。

证：截面切应力 4103s R R ρρττρ⎛⎫=-≤≤ ⎪⎝⎭截面扭矩 04d 12πd 03Rs s A T A R ρρτρτρρ⎛⎫==-⋅= ⎪⎝⎭⎰⎰ 证毕。

12. 图示直径为d 的实心圆轴,两端受扭转力偶e M 用1/m C τγ=表示，式中C ，m 为由实验测定的已知常数，试证明该轴的扭转切应力计算公式为：1/e (31)/2π()23m 1mm mM m d ρρτ+=+s /3证：几何方面 d d xρϕγρ= 物理方面 1/1/d d mmC C x ρϕτγρ⎛⎫== ⎪⎝⎭静力方面 1//21/e 0d d 2πd d md mAM T A C x ρϕρτρρρρ⎛⎫==⋅⋅=⋅⋅ ⎪⎝⎭⎰⎰1//221/0d 2πd d m d mC x ϕρρ+⎛⎫= ⎪⎝⎭⎰(31)/1/()d 22π(31)d m mmd C m x mϕ+⎛⎫= ⎪+⎝⎭1/e (31)/(31)d d 2π()2mm m M m d x Cm ϕ++⋅⎛⎫=⎪⎝⎭⋅ 所以 1/e (31)/2π()23m 1mm mM m d ρρτ+=+ 证毕。

材料力学 扭转 计算公式及例题

0.1994 已知
Ip
m4
0.1
求
Ip m4
4.00E-02
求
Ip m4
1.00E-01
求
WP m3
1.99E-01
求
WP m3
1.00E-01 求 d mm
1.01E+03 求 d mm
1.00E+03
数据状态 代号 单位 数值
数据状态 代号 单位 数值
已知 φ ° 1 已知 θ °/m 2
已知
求
代号 θmax
Ip Mn max
G [θ]
单位 °/m
m4 N·m Pa °/m
序号 1 2 3
名称 外力偶矩
功率 转速
代号 T NK n
序号
1 2 3
名称
横截面上的最大扭矩 抗扭截面模量 材料许用切应力
代号 圆轴扭转时的强度条件
Mn max WP
[τ]
序号
名称
强度计算
代号
1
横截面上的最大扭矩
2
Wp
πD3 16
公 圆式柱 公圆式柱 形， 形，
求
WP
m3
1.00E-01 求 d mm
1.01E+03 求 d mm
1.00E+03
公式
圆柱形，实心
Ip
πD 4 32
Wp
πD3 16
公式
公式
圆柱形，空心
圆柱形，薄壁
I
p
π（D4 32
d4）
πD4（1- 32
4）
Ip 2πr03t
Wp
πD3
已知 Mn(AC) K N·m 1.43
已知 G MPa

材料力学圆形扭转知识点总结

材料力学圆形扭转知识点总结材料力学是研究物体受力和变形的学科，而圆形扭转是材料力学中的重要内容之一。

本文将对圆形扭转的知识点进行总结和介绍。

1. 扭转概述扭转是指沿一个固定轴线施加一个力矩使物体发生旋转。

在材料力学中，圆形扭转是指柱状材料沿轴向受到一个偶力矩而发生形变的过程。

2. 扭转角和扭转变形扭转角是指材料在扭转过程中单位长度所扭转的角度。

扭转变形表示材料的单位长度所发生的变形，主要包括剪切应力和剪切应变。

3. 圆柱体扭转方程在圆形扭转中，我们可以通过圆柱体的几何形状和物体的力学性质来建立扭转方程。

圆柱体扭转方程可以用来描述扭转角、剪切应力和剪切应变之间的关系。

4. 扭转刚度和扭转弹性模量扭转刚度是指单位长度的材料所承受的扭矩与扭转角度之间的比值。

扭转弹性模量是材料在扭转过程中所表现出的抗扭刚度大小的指标。

5. 扭转应力和扭转应力分布扭转应力是指扭转过程中由力矩引起的单位面积上的应力。

在圆形扭转中，扭转应力的分布与材料的截面形状和外力矩的大小有关。

6. 主要扭转方程主要扭转方程是指圆形扭转中计算剪切应力、剪切应变和扭转角的方程。

根据不同的材料和几何形状，有多种扭转方程可供选用。

7. 圆形扭转的工程应用圆形扭转在工程领域中具有广泛的应用。

例如，在轴承、传动轴和液压机械等领域中，圆形扭转的知识可以帮助工程师设计和分析各种机械零件。

8. 实验测量和分析对于圆形扭转现象的研究，实验测量和分析是必不可少的部分。

通过设计和进行合适的实验，可以获取材料的扭转性质，并对材料的力学行为进行深入研究与分析。

总结：圆形扭转是材料力学的重要内容之一，它涉及到材料的扭转角、扭转变形、扭转刚度、扭转弹性模量、扭转应力和扭转应力分布等知识点。

通过对圆柱体扭转方程和主要扭转方程的研究与应用，可以帮助工程师设计和分析各种机械零件。

实验测量和分析对于深入了解圆形扭转现象和材料的力学行为也起着重要作用。

对圆形扭转的深入了解有助于我们在工程实践中更好地应用材料力学的知识。

材料力学扭转详细讲解和题目非常好

材料力学 扭转扭转的概念扭转是杆件变形的一种基本形式。

在工程实际中以扭转为主要变形的杆件也是比较多的，例如图6-1所示汽车方向盘的操纵杆，两端分别受到驾驶员作用于方向盘上的外力偶和转向器的反力偶的作用；图6-2所示为水轮机与发电机的连接主轴，两端分别受到由水作用于叶片的主动力偶和发电机的反力偶的作用；图6-3所示为机器中的传动轴，它也同样受主动力偶和反力偶的作用，使轴发生扭转变形。

图6—1 图6—2 图6—3这些实例的共同特点是：在杆件的两端作用两个大小相等、方向相反、且作用平面与杆件轴线垂直的力偶，使杆件的任意两个截面都发生绕杆件轴线的相对转动。

这种形式的变形称为扭转变形（见图6-4）。

以扭转变形为主的直杆件称为轴。

若杆件的截面为圆形的轴称为圆轴。

图6—4扭矩和扭矩图6.2.1 外力偶矩作用在轴上的外力偶矩，可以通过将外力向轴线简化得到，但是，在多数情况下，则是通过轴所传递的功率和轴的转速求得。

它们的关系式为 nP M 9550= （6-1） 其中：M ——外力偶矩（N ·m ）;P ——轴所传递的功率（KW ）；n ——轴的转速（r ／min ）。

外力偶的方向可根据下列原则确定：输入的力偶矩若为主动力矩则与轴的转动方向相同；输入的力偶矩若为被动力矩则与轴的转动方向相反。

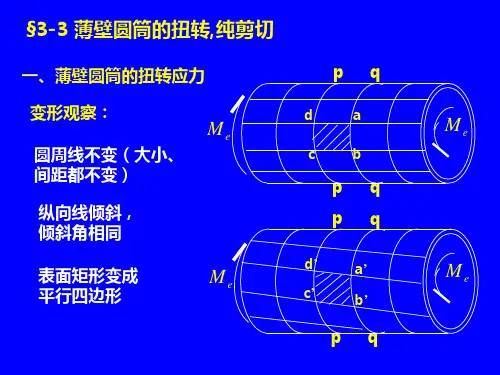
6.2.2 扭矩圆轴在外力偶的作用下，其横截面上将产生连续分布内力。

根据截面法，这一分布内力应组成一作用在横截面内的合力偶，从而与作用在垂直于轴线平面内的外力偶相平衡。

由分布内力组成的合力偶的力偶矩，称为扭矩，用n M 表示。

扭矩的量纲和外力偶矩的量纲相同，均为N·m 或kN·m。

当作用在轴上的外力偶矩确定之后，应用截面法可以很方便地求得轴上的各横截面内的扭矩。

如图6-5（a ）所示的杆，在其两端有一对大小相等、转向相反，其矩为M 的外力偶作用。

为求杆任一截面m-m 的扭矩，可假想地将杆沿截面m-m 切开分成两段，考察其中任一部分的平衡，例如图6-5（b ）中所示的左端。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

y
5.2.2 切应力互等定理
dz
'
取一单元体
左、右侧面 切应力τ 力τdydz
dy
O
x
'
力偶矩 (τ dydz)dx z
dx
上、下侧面
切应力τ'
力τ' dydz
力偶矩(τ' dxdz)dy 平衡条件∑Mz = 0得
τdydzdx-τ′dxdzdy=0
τ = τ′
切应力互等定理
y
在单元体相互垂直的截面上， dz
n
T Me
Me I n
作用于横截面上的内力偶矩称为扭矩 b)
T
x
n
由作用与反作用原理可知，在
部分Ⅱ横截面n-n上也必然有
n
II
Me
大小相等、转向相反的扭矩T c) T
x
n
发生扭转变形的外力偶矩，称为扭转力偶矩
1. 已知外力
Me (FT1 FT2 )R
R
FT1
FT2
2. 已知传递的功率P(kW)和转速n(r/min)
得
P
M e
Me
2 n
60
Me
9549
P n
(N m)
5.2 纯剪切状态与切应力互等定理
5.2.1薄壁圆筒的扭转时的切应力与纯剪切状态
一、实验观测
Me
Me
在圆筒表面画一系列纵
R
向线和圆周线。
现象
a)
(1) 纵向线都倾斜了相同的角度，变为平行的螺旋线。
(2)圆周线绕杆轴线旋转了不同的角度，但仍保持为 圆形，且在原来的平面内。
0
Wp
πD3 16
(2) 空心圆截面 d / D
Ip
O1
O2
R
F
d
E A
H
B F1
B1 G
D
C G1
C1
dx
b)
5.3.3．物理方面 根据剪切胡克定律，在线弹性范围内，切应力 与切应变成正比。 横截面上半径为ρ 处的切应力为
G
(1)横截面的切应力与该点到圆心的距离ρ成正比。
(2) 纵向截面上的切应力也沿半径线性变化。
dA
max
dA
O
a)
b)
5.3.4．静力学方面
微力矩 dA
截面上的扭矩
T
A
dA
dA
max
dA
O
为常量，得 a) T G 2dA A
引进记号
Ip
2dA
A
Ip称为横截面对圆心的极惯性矩
T
GIp
圆轴单位长度扭转角的计算公式
5.3.5 圆轴扭转时横截面上的切应力表达式
圆轴横截面上任一点处的切应力
T
Ip
5.4.2 圆轴扭转强度条件
τmax
Tm a x Wp
[τ]
(1) [ ] 为材料的许用切应力
(2) 对于等直轴，最大切应力发生于扭矩最大截面 上的外边缘。
(3) 对变截面轴,需要综合考虑T和Wp来确定τmax。
D
极惯性矩与抗扭截面系数
(1) 实心圆截面
Ip
ρ2dA
D
/
2
2
Hale Waihona Puke 3dπD4A32
AC段 DB段
AC max
16TAC
d13
16 763.9
(40 103)3
60.8MPa [ ]
DB max
16TDB
d
3 2
16 1909.8
(60 103)3
45.0 MPa [ ]
轴满足强度要求。
• 5.4 圆杆扭转时的强度和刚度计算
• 5.4.1 圆轴扭转实验与破坏现象 • 1 观察变形现象：
解 (1)计算外力偶矩， 画扭矩图
P1
a)
A
P2
d1
C
D
P3
d2
B
M e1
9549
24 300
763.9
N
m
0.5 m 0.3 m 1.0 m
T /Nm
Me2
9549
36 300
1145.9
N
m b)
763.9
(-)
x
M e3
9549
60 300
1909.8
N
m
1909.8
(2)校核扭转强度
尽管最大扭矩发生在DB段内，但这一段截面的直 径也大，对AC和DB两段轴都需要作强度校核。
•
• 2 变形现象：
• （1）纵线在变形后近似为直线，
• 但相对于原位置转了一个 角。 • （2）环线变形后仍相互平行，产生了剪应变。 • 3 推论： • （1）圆杆在扭转后横截面保持为垂直杆轴线的平面， • 且大小、形状不变，半径为直线。 • （2）用纵线和环线截取的单元体处于纯剪切状态。 • （3）圆杆的横截面上只有剪应力作用，方向垂直于半径。
第五章 圆轴扭转
§5-1 外加力偶矩与所传递功率的关系 §5-2 纯剪切状态与切应力互等定理 §5-3 圆轴扭转时的切应力分析 §5-4 圆轴扭转时的迁都与刚度计算 §5-5 结论与讨论
5.1 外加力偶矩与所传递功率的关系
求横截面n-n上的内力偶矩 Me I n
截面法
a)
II
Me
Mx 0 T Me 0
'
切应力必然成对出现，且大小
相等，方向都指向(或背离)两
dy
O
平面的交线
x
'
纯剪切应力状态
z
dx
单元体侧面上只有切应力，没有正 应力的状态称为纯剪切应力状态。
5.2.3 剪切胡克定理
直角的改变量即为切应变
低碳钢的 - 曲线
在弹性极限范围内
G
s p
上式称为剪切胡克定理。
G称为材料的切变模量,单位为帕(Pa)
5.3.2．变形协调方程
取长为dx的微段
两截面的相对扭转角为 d
从该微段中切取一楔形体 由几何关系及小变形假设
γρ
tanγρ
FF1 EF
d
dx
表示扭转角φ沿轴线的变化
率，称为单位长度扭转角
在同一半径为ρ的圆周上， 各点处的切应变γρ均相同， 且与ρ成正比。
O1
A
D
d
O2 B B1 C
C1
dx
a)
推断：(a)变形后，横截面仍保持为平面； (b)横截面上没有正应力，只有切应力， 切应力的方向与半径垂直。
二、切应力的计算 研究薄壁筒的任一横截面
Me
T
d
dA
微面积 dA = δRdθ
dA
b)
微内力τdA对截面形心的力矩为τdA·R
横截面上的扭矩
即 积分得
dA R T
A
2π τR 2d T 0 τ T 2πR2
'
'
切变模量G、弹性模量E和泊松比三者之间的关系是
G E
2(1 )
5.3 圆轴扭转时的切应力分析
5.3.1 平面假定
圆轴扭转的平面假设
变形前为平面的横截面，在变形后仍保持为 平面，半径仍保持为直线，各横截面的形状、 大小及间距均不改变。
圆轴扭转时横截面上的应力可以从三个方面导出 1．几何方面
2．物理方面 3．静力学方面
切应力达到最大值
引进记号
τmax
TR Ip
Wp
Ip R
Wp称为抗扭截面系数。
说明：
τ
m
ax
T Wp
(1)只适用于弹性范围内的等直圆轴
(2)对于小锥度圆轴，也可以用以上各式近似地计算。
例 图3-13a所示阶梯形圆轴直径分别为d1 = 40 mm，d2 = 60 mm。由轮3输入的功率P3 = 60 kW，轮1输出的功率 P1 =24 kW。轴作匀速转动，转速n = 300 r/min。材料 的许用切应力 [ τ ] = 70 MPa。试校核轴的强度。