当前位置：文档之家 › 材料力学第4章-圆轴扭转_3260334

材料力学第4章-圆轴扭转_3260334

  • 格式：ppt
  • 大小：3.39 MB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

第4章 扭转

第4章 扭转

4.1 概述
某轮传递功率P=30kW ，转数 n = 300 rpm， 例： 某轮传递功率 ， 则它对轴作用的外扭转力偶矩为? 则它对轴作用的外扭转力偶矩为
30 P Me = 9549 = 9549 n 300
= 954.9 N ⋅ m
思考：如果传递的功率单位为马力（ ， 思考：如果传递的功率单位为马力（PS)，那麽公 式会怎样？ 式会怎样？
W= t
πD3
16
(1−α ) =
4
π ×903
16
3) 校核强度。 校核强度。
τmax
90 − 2×15 1− 90
4
=114.9×103 mm3
Tmax 9.56×106 = = = 83.2M > [τ]=80MPa Pa 3 W 114.9×10 t
扭转切应力
τρ
Tρ = Ip
4.4 圆轴扭转时的应力 强度条件
5. 最大切应力 当 ρ = ρmax
τ max
式中
T = Wt
Wt =
Ip
ρmax
称抗扭截面系数，单位： 称抗扭截面系数，单位：m3.
ห้องสมุดไป่ตู้
4.4 圆轴扭转时的应力 强度条件
Ip和Wt公式
Ip =
D
πD4
32
W = t
πD3
16
Ip =
d
MC 2 C MD 3 D
4.2 扭矩 扭矩图
2)计算轴上各段的扭矩 计算轴上各段的扭矩 BA段：∑Mx =0 段 T1 = -MB =-2387.25Nm
MB B T1 MB B MA A T3 MD D T2
AC段：∑Mx =0 段 T2 = MA−MB=2387.25Nm CD段：∑Mx =0 段 T3 =MD = 954.9Nm 3) 作扭矩图 按比例绘出扭矩图如右所示。 按比例绘出扭矩图如右所示。

第4章扭转变形 材料力学,力学,物理,课件

第4章扭转变形 材料力学,力学,物理,课件
[ ] (0.8 1.0)[ ]
二、强度条件
max [ ]
工作应力
材料的许用切应力
等直圆轴 三类强度计算：
Tmax [ ] Wp
Tmax [ ] Wp
1、强度校核 max 2、截面设计
Tmax Wp [ ]
3、确定许可载荷 Tmax Wp [ ]
R1
R2
O
T Ip
T
空心轴
max
O
T Wp
薄壁圆管扭转切应力
dS
dS
A
Bபைடு நூலகம்
R0
o
T
由于管壁薄，可以认为扭转切应力沿壁厚均 匀分布 T 2R02 思考：公式的精度？

max
R0
在线弹性情况下，精确解为
max
16T D3 1 4
R0 , 误差 4.53% 10
d G dx
公式中还有哪些量未被确定？ 3. 静力学方面


A
dA T
定义： I p
dA
d G dx

A
2dA T
极惯性矩

A
2dA
O
T
d T dx GI P T IP
扭转角变化率 圆轴扭转切应力的 一般公式。
圆轴扭转时横截面上切应力计算公式：
M M
M
M
截面尺寸突变
配置过渡圆角
例1 一传动轴如图，转速n = 300r/min ,d=110mm; 主动轮输入 的功率P1= 500kW，三个从动轮输出的功率分别为： P2= 150kW， P3= 150kW， P4= 200kW。 (1) 试求传动轴截面2-2上距轴线40mm处的点的切应力。 (2) 若已知[τ]=40MPa，试校核轴的强度。

材料力学课件 第四章 扭 转

材料力学课件 第四章 扭 转

1. 横截面变形后
仍为平面；
2. 轴向无伸缩；
3. 纵向线变形后仍为平行。
圆轴横截面应力
①变形几何方面
②物理关系方面
精选课件 ③静力学方面
20
精选课件
21
二、等直圆轴扭转时横截面上的应力：
1. 变形几何关系：
tgG d1G xd d x
d
dx
距圆心为 任一点处的与到圆心的距离成正比。
d dx
—— 扭转角沿长度方向变化率(单位长度扭转角)。
T
Ip
精选课件
24
T
Ip
—横截面上距圆心为处任一点切应力计算公式。
薄壁圆筒体扭转实验
精选课件
17
T=m
在一定范围内
T (2A0t) (L/R)
剪切虎克定律：当切应力不超过材料的剪切比例极限时
（τ ≤τp) (在弹性范围内)，切应力与剪应变成正比关系。
精选课件
18
G
式中：G是材料的一个弹性常数，称为剪切弹性模量，因 无 量纲，故G的量纲与 相同，不同材料的G值可通过实验确定，钢
´
a
b
mz 0
dy
t dxdy t dxdy
´
c
d
故
t
z
dx
上式称为切应力互等定理。
该定理表明：在单元体相互垂直的两个平面上，切应 力必然成对出现，且数值相等，两者都垂直于两平面的交 线，其方向则共同指向或共同背离该交线。
精选课件
16
单元体的四个侧面上只有切应力而无正应力作用，这 种应力状态称为纯剪切应力状态。 四、剪切虎克定律：
③绘制扭矩图 T 9.56kN mBC段为危险截面。 max

材料力学第4章扭转

材料力学第4章扭转
页 退出
材料力学
出版社 理工分社
下面分析圆轴内任意点的应变。为此，用相邻的两个横截面p—p和q—q从圆 轴上取出微段dx，并放大为如图4.10(a)所示。根据平面假设，q—q截面相 对于p—p截面的扭转角为dφ，半径Oa转到了Oa′。于是，表面方格abcd的ab 边相对于cd边发生了微小的错动，错动的距离为
出版社 理工分社
(2)圆轴扭转时斜截面上的应力 在圆轴的扭转试验中，可以发现这样一种现象：低碳钢试件的破坏是沿构件 的横截面断开的，断口比较平整、光滑，如图4.14(a)所示；而铸铁试件的 破坏则是沿着与轴线约成45°角的螺旋形曲面断开的，断口呈细小颗粒状， 如图4.14(b)所示。为了解释这种现象，有必要研究圆轴扭转时斜截面上的 应力。
页 退出
材料力学
出版社 理工分社
图4.7
页 退出
材料力学
出版社 理工分社
(3)剪切胡克定律 通过薄壁圆筒的扭转实验可以得到材料在纯剪切应力状态下应力与应变之间 的关系。 试验结果表明，当切应力低于材料的剪切比例极限时，相对扭转角φ与扭矩 T之间成正比。而由图4.6(b)所示的几何关系可求得薄壁圆筒表面上的切应 变γ和相距为l的两端面之间的相对扭转角φ之间的关系为
页 退出
材料力学
出版社 理工分社
图4.11
页 退出
材料力学
出版社 理工分社
3)静力关系
式(4.8)中， 尚未确定，所以需进一步考虑静力关系，才能求出圆轴扭转
时横截面上一点的切应力。
如图4.12所示，在横截面上距圆心O为ρ的地方取微面积dA，其上的微内
力
对圆心O的力矩为
。显然， 遍及整个横截面的积分，
结合式(4.2)和式(4.4)可以看出，切应力与T成正比，而切应变γ又与φ成 正比。所以，当切应力不超过材料的剪切比例极限时，切应变γ与切应力成 正比(见图4.8)，即

04.圆轴的扭转

04.圆轴的扭转
当在轴的右端作用一力偶 矩m时，圆轴各相邻截面之 间也都发生了绕各自截面轴 心的相对转（错）动。假设 圆轴不长，扭转变形又不是 很大，则纵向线在变形后仍 可近似地看成是一条直线， 只是倾斜了一个角度γ。
一、圆周扭转时的变形分析（续1）
2. 变形分析： 假想沿n-n和m-m两个相距dx的横截面将轴切取一薄
四指沿扭矩的方向屈起， 拇指的方向离开截面，扭 矩为正，反之为负。
三、横截面的内力矩——扭矩（续2）
3.扭矩正负号的规定：
（1）右手螺旋法则：
四个手指沿扭矩转动的方向，大拇指即为扭矩的方向。
（2）扭矩正负号：
离开截面为正，指向截面为负。 （3）外力偶矩正负号的规定：
指向截面
与坐标轴同向为正，反向为负
' 量显然可以用弧线 ：c c 表示，其值为：
(书P54）
cc' Rd
n-n截面在b点处的 角应变：
g＝cc' R d (5-5)
dx dx
一、圆周扭转时的变形分析（续3）
观察截面n-n上距圆心为ρ处的bρ 点， 如左图，bρ点处的角应变：
g
＝
c c' dx
d
dx
(5-6)
d 表示扭转角沿轴线x的变化率，为两个截面相隔单
g
Mn
B
x
j
B'
1.受力特点：构件两端受到两个在垂直于轴线平面内的 力偶作用，两力偶大小等，转向相反。
2.变形特点：各横截面绕轴线发生相对转动。 3.扭转角：任意两截面间有相对的角位移，这种角位移
称为扭转角。
轴的概念
工程上，将以扭转变形为主要变形的构件通 称为轴。（对比：以弯曲为主要变形的构件在工 程上通称为梁)同时，多数轴是等截面直轴。

材料力学第4章扭转变形

材料力学第4章扭转变形

1 1
T
1 1
T
1
Me
+
B
x
T Me
Me
B
T图 x
例 一传动轴如图，转速n = 300r/min； 主动轮输 入的功率P1= 500kW，三个从动轮输出的功率分 别为： P2= 150kW， P3= 150kW， P4= 200kW。 试作轴的扭矩图。
解： 首先必须计算作用在各轮上的外力偶矩
M2 1
2 T
1
1 T
1
材料不同），可见在两
杆交界处的切应力是不
同的。
d
D
§4. 7 非圆截面杆扭转的概念
对非圆截面杆的扭转问题，主要介绍矩形截面 杆的扭转。
试验现象
横向线变 成曲线
横截面发生 翘曲不再保 持为平面
平面假设不再 成立，可能产 生附加正应力
自由扭转 翘曲不受限制。 纵向纤维无伸长 横截面上无正应力
T
max
O
max
D
d
T
Ip
max
T Wp
圆截面的极惯性矩Ip和扭转截面系数Wp —几何性质 实心圆截面：
d
O
d
O
d D d
Ip
2 d A πd 4
A
32
Wp
Ip d /2
πd 3 16
Ip
2 d A πD4
A
32
1 4
Wp
Ip D /2
πD 3 16
1 4
4-4 圆轴扭转强度条件与合理设计
B 0
按叠加原理：
B BB BM 0
BB、BM分别为MB、Me 引起的在杆端B的扭转角。
线弹性时，物理关系(胡克定理)为

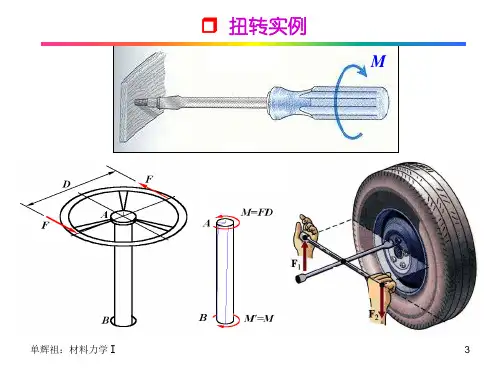
材料力学第四章扭转

材料力学第四章扭转

解：1、变形 协调条件
1 2
2、装配扭力
偶矩 M
l1
l2
d1
d2
D
M
1
2
M
M FS
Page45
第四章 扭转
1 2
M
D
3、 M 关系
1
2
M
1
32Ml1
G d14
2
32Ml2
G
d
4 2
4、装配扭力 偶矩解答
M G d14d24
32
l1d
4 2
l2d14
5、轴最大切应力
1,max
16M
§4-2 扭矩
1. 扭矩与扭矩图
m
M
A
M
m
B
A
mT
x
M
m
扭矩：矢量方向垂直于横截面 A
m
Tx
的内力偶矩，并用T 表示。 M
m
符号规定：矢量方向(按右手定则)与横截面外法线方
向一致的扭矩为正，反之为负。
Page 6
第四章 扭转
扭矩图：扭矩随杆轴线变化的图线。
例：画扭矩图。
在AB和BC段分别切开， 分别考察左与右段平衡
max
A:
2M
D3
,
16
M
B :
D3
14
16
max
Page32
第四章 扭转
4、刚度校核
m 2M a
A
BM
3M
dD
a
a
a
a
x
T
M
T 2M x a
B
2M
A
x
max
max

材料力学：第4章 扭转

材料力学：第4章 扭转

例题 图示传动轴上，经由A轮输入功率10KW，经由B、C、D轮 输出功率分别为2、3、5KW。轴的转速n=300r/min，求作该轴 的扭矩图。如将A、D轮的位置更换放置是否合理？
A
B
C
D
I
II
III
I
II
III
第四章 扭转/二 外力偶矩、扭矩和扭矩图
解： 经由A、B、C、D轮传递的外力偶矩分别为
mA
9.549
PA n
9.549
10 300
318.3(N
m)
mB
9.549
PB n
9549 2 300
63.7(N m)
mC 95.5(N m),
M D 159.2(N m),
A
B
C
D
I
II
III
I
II
III
第四章 扭转/二 外力偶矩、扭矩和扭矩图
mB
I
I M n1
mB
MC
III
mn3
m2
9550 120
557 N .M
,m3ຫໍສະໝຸດ 9550360185.7
max(E)= m1
Wp1
1114
d 3
1114
(0.07)3
16
16
= 16.54 MPa
m2
max(H)=
= 22.69 MPa
d
dx
G
G
d
dx
Mn
IP
dA M n
A
G
d
dx
A
2dA
M
n
d MT n
dx GIP
Ip 截面的极惯性矩
(3)受扭圆轴横截面上的剪 应力计算公式

材料力学：第四章 扭转

材料力学：第四章 扭转

回顾: 极惯性矩、抗扭截面系数的计算
抗扭截面系数 极惯性矩
薄壁圆管 扭转切应力
回顾: 圆轴扭转强度条件 & 应力计算公式
薄壁圆管扭 转切应力
圆轴扭转 强度条件
max
[ ] u
n
扭转极限应力τu =
扭转屈服应力ts (塑性材料) 扭转强度极限tb (脆性材料)
§5 圆轴扭转变形与刚度计算
单辉祖：材料力学Ⅰ
14
例题
例 2-1 MA=76 Nm, MB=191 Nm, MC=115 Nm, 画扭矩图 解：用截断法,列力偶
矩平衡方程,和x轴正向 相同者取正 (1) 1-1截面
单辉祖：材料力学Ⅰ
(2) 2-2截面 T2 MC 115 N m
(3) 画扭矩图
15
§3 圆轴扭转横截面上的应力
单辉祖：材料力学Ⅰ
64
薄壁杆扭转
开口与闭口薄壁杆
截面中心线
－截面壁厚平分线
薄壁杆
－壁厚<<截面中心线 长度的杆件
闭口薄壁杆
－截面中心线为封闭曲线的薄壁杆
开口薄壁杆
－截面中心线为非封闭曲线的薄壁杆
单辉祖：材料力学Ⅰ
65
闭口薄壁杆扭转应力与变形
假设 切应力沿壁厚均匀分布, 并平行于中心线切线 应力公式
单辉祖：材料力学Ⅰ
62
例题
例 7-1 试比较闭口与开口薄壁圆管的抗扭性能,设 R0＝20d
解：1. 闭口薄壁圆管
2. 开口薄壁圆管
3. 抗扭性能比较
单辉祖：材料力闭学Ⅰ口薄壁杆的抗扭性能远比开口薄壁杆好
63
§8 薄壁杆扭转
开口与闭口薄壁杆 闭口薄壁杆扭转应力与变形 开口薄壁杆扭转简介 薄壁杆合理截面形状 例题

材料力学第4章-圆轴扭转_314802849

材料力学第4章-圆轴扭转_314802849

dx
第4章 圆轴扭转时的强度与刚度计算
圆轴扭转时横截面上的剪应力分析与强度设计
Mx A
r
C
d
r A O B
r
Cc C' d

O O a b c c' d
d
O d'
C'
B
D
D'
D D'

dx
dx
dx
r dx rd
dx d
第4章 圆轴扭转时的强度与刚度计算
第4章 圆轴扭转时的强度与刚度计算
圆轴扭转时横截面上的剪应力分析与强度设计
平面假定
变 形 应变分布
物性关系
应力分布
变形协调+物性关系+平衡方程
Me Mx
静力方程
n
Mx
应力公式
假定：圆轴受扭发生变形后，其横截面 依然保持平面，刚性地转过一角度。这 一假定称为平面假定。
第4章 圆轴扭转时的强度与刚度计算
圆轴扭转时横截面上的剪应力分析与强度设计
变形协调+物性关系+平衡方程
Mx
静力学方程
d

O

dA M
A
x

第4章 圆轴扭转时的强度与刚度计算
圆轴扭转时横截面上的剪应力分析与强度设计
变形协调+物性关系+平衡方程 d dA M x G G
d dx
dx
y

A C
dy
B

dz
x
d G G dx
z
dx D
第4章 圆轴扭转时的强度与刚度计算

第四章 扭转

第四章 扭转

(在线弹性范围内)
§4-4 等直圆轴扭转时的应力〃强度条件
一、等直圆轴扭转时的应力
Me

Me
r

实验： 变形现象： (1)圆周线绕轴线相对转动； (2)圆周线大小和间距不变； (3)径向直线仍然保持为直线； (4) 纵向线倾斜同一角度； (5)矩形变为菱形。

—切应变
●平面截面假设 圆轴扭转变形前的横截面，变形后仍保持为平面， 大小和形状不变，半径仍保持为直线，任意两横截面 间的距离保持不变，但绕轴线发生相对转动。
M2 4.78 B T (kN· m) 4.78
Tmax = 9.56 kN· m M3 4.78
C 9.56 M4 6.37 A 9.56 15.9 Tmax = 15.9 kN· m M1 15.9
(kN.m)
D
● 主动轮与从动论位臵的合理安排： 主动轮放在从动论之间，并尽量使两边从动论所 传递的外力偶矩相等。
例2. 轴受力如图所示，画出轴的扭矩图。
Me=2ma
1
m 2
m—分布力偶矩 单位：kN· m/m x
C
A
1 B
2
a
2a
T1 2ma
2ma
T2 mx
扭矩方程
T
(0 x 2a )
分布力偶矩作用的段，扭矩图是斜直线。
§4-3 薄壁圆筒的扭转
一、 薄壁圆筒的扭转 1. 薄壁圆筒
Me 1 Me

4
d4
D4
32
4
1
4
D 4
O
32 IP D 3 1 4 Wt D / 2 16
1
d D
三、强度条件

材料力学课件 第四章扭转

材料力学课件 第四章扭转
4. 公式讨论： ① 仅适用于各向同性、线弹性材料，在小变形时的等圆截面
直杆。
② 式中：T—横截面上的扭矩，由截面法通过外力偶矩求得。
—该点到圆心的距离。
Ip—截面极惯性矩，纯几何量，无物理意义。
17
Ip A 2dA 单位：mm4，m4。
③ 尽管由实心圆截面杆推出，但同样适用于空心圆截面杆，
只是Ip值不同。
一、传动轴的外力偶矩 传递轴的传递功率、转数与外力偶矩的关系：
m
9.55
P n
(kN
m)
其中：P — 功率，千瓦（kW） n — 转速，转/分（rpm）
m
7.024
P n
(kN
m)
其中：P — 功率，马力（PS） n — 转速，转/分（rpm）
m
7.121
P n
(kN
m)
其中：P — 功率，马力（HP） n — 转速，转/分（rpm）
22
[例2]有一阶梯形圆轴，如图(a)所示轴的直径分别d为1 50mm,d2 80mm 。扭转力偶矩分别为 Me1 0.8kN m ，Me2 1.2kN m ，M e3 2kN m。若 材料的许用切应力 [ ] 40MPa ，试校核该轴的强度。
解： 方法一（理论计算法） 用截面法求出圆轴各段的扭矩，如图(b)所示。 由扭矩图可见，CD段和DB段的直径相同，但DB段的扭矩大 于CD段，故这两段只要校核DB段的强度即可。AC段的扭矩 虽然也小于DB段，但其直径也比DB段小，故AC段的强度也 需要校核。
2GI p
W
U ;
64PR3n Gd 4
P K
;
K
Gd 4 64R3n
为弹簧常数。
36
[例3] 圆柱形密圈螺旋弹簧的平均直径为：D=125mm，簧丝直 径为：d =18mm，受拉力 P=500N 的作用，试求最大剪应力 的近似值和精确值；若 G =82GPa，欲使弹簧变形等于 6mm， 问：弹簧至少应有几圈？

材料力学-第4章 扭转

材料力学-第4章 扭转
18
材料力学－第4章 扭转
圆轴扭转横截面上的应力

变 形
O
dx
ρ
R A

d
O’
( ) G G
d
dx
应变特征

B B´
A


B B´
应力分布

C
C
D D´

D D´
应力公式
BB Rd G G G AB dx
19
材料力学－第4章 扭转
圆轴扭转横截面上的应力
材料力学
第四章 扭 转
1
材料力学－第4章 扭转
内容提纲：
• • • • • • • • 概述及示例 外力偶矩、扭矩和扭矩图 圆轴扭转横截面上的应力 圆轴扭转破坏与强度条件 圆轴扭转变形与刚度条件 扭转静不定问题 非圆截面轴扭转 薄壁杆扭转
2
材料力学－第4章 扭转
概述及示例
3
材料力学－第4章 扭转
9
材料力学－第4章 扭转
扭力偶矩计算与扭矩
• 在工程中，功率常用千瓦 Pkw (kW) 或马力 P 给出，角 速度用转速 n(r/min (转/分钟)) 给出，则外力偶矩的计算 公式为
PkW M e 9549 nr /min M e 7024 P 马力 nr /min
1 Pkw (千瓦) 1000 N m /s 1 P (马力) 735.5 N m /s

45o
32
材料力学－第4章 扭转
圆轴扭转破坏与强度条件
从破坏类型可见，对于脆性材料（如铸 铁），其破坏机理是斜截面上的最大拉应力 因此，本质上讲，应对斜截面上的正应力 进行强度计算。然而，由于斜截面上的正应力和 横截面上的剪应力间有固定的关系，所以，习惯 上仍按最大剪应力进行强度计算

第4章扭转

第4章扭转

max
G[ ] T max GI p [ ] Ip T
PA M eA 9550 1146N m n PB M eB M eC 9550 350N m n PD M eD 9550 477.5N m n
(2)用截面法，根据平衡方程计算各段内的扭矩。
T1 M eB 0
T1 M eB 350N m
塑性材料 脆性材料
材料力学
第4章 扭转
Wt 的计算
对于直径为D的实心圆轴来说
dA 2 d
D4
32
I P 2 dA
A
D 2
0
2 2 d
3
Wt
IP D D 16 2
2
对于内径d、外径D的空心圆轴来说
I P dA d 2 d
材料力学
第4章 扭转
4.4 圆轴扭转时的应力与强度条件
4.4.1 圆轴扭转时的应力计算 等直圆轴扭转 实验观察:
(1) 各圆周线绕轴线相对转动一微小转角，但大小、形状及相互间距不变； (2) 各纵线平行地倾斜一个微小角度 ，认为仍为直线；而各小矩形变形后成 为平行四边形。
材பைடு நூலகம்力学
第4章 扭转
圆轴扭转的平面假设：变形前为平面的横截面变形后 仍为平面，它像刚性平面一样绕轴线旋转了一个角度。
材料力学
第4章 扭转
第4章 扭转
3、静力平衡关系
T A dA d A G dA dx
2
Ip为截面对 圆心O的极
惯性矩
dA

d G A 2dA dx
令：I p A 2dA
d T dx GI p

材料力学-第4章 扭转

材料力学-第4章 扭转

低炭钢：抗压>抗拉>抗剪强度
脆性材料：受拉破坏

铸铁：抗压>抗剪>抗拉强度
45o
38
材料力学－第4章 扭转
圆轴扭转破坏与强度条件
从破坏类型可见，对于脆性材料（如铸 铁），其破坏机理是斜截面上的最大拉应力
因此，本质上讲，应对斜截面上的正应力 进行强度计算。然而，由于斜截面上的正应力和 横截面上的剪应力间有固定的关系，所以，习惯 上仍按最大剪应力进行强度计算
扭转圆轴不同平面上的应力分布
切应变：


d
dx
切应力： ()
G
G
d
dx
O
dx
O’
A
B
C
D
max
25
材料力学－第4章 扭转
圆轴扭转横截面上的应力


G
d
dx
• 切应力方向垂直于半径（由于剪切变形发生 在垂直于半径的平面内）
• 圆轴截面上的切应力与 成正比
max
外力偶矩的计算
• 工程中的传动轴，通常给出传动轴所传递的功 率和转速，而不直接给出外力偶矩的数值
• 设外力偶矩为Me，传动轴的功率为P，角速度 为w，则有（理论力学）
P
Me w
外力偶矩Me 单位：N·m (牛顿·米) 功率为P 单位：J (焦耳)
角速度w 单位：arc/s (弧度/秒)
9
材料力学－第4章 扭转
T WP
R
其中：
WP

d3
16
称为抗扭截面系数
30
材料力学－第4章 扭转
圆轴扭转横截面上的应力
实心圆轴好？空心圆轴好？
实心圆轴，靠近圆心部分面积上切应 力极小。单位面积上承载的扭矩远小于 离圆心较远处。因此，工程上受扭圆轴 多采用空心圆轴

《材料力学》第4章 扭转

《材料力学》第4章 扭转

第4章 扭转§4-1 概述工程上的轴是承受扭转变形的典型构件，如图4-1所示的攻丝丝锥，图4-2所示的桥式起重机的传动轴以及齿轮轴等。

扭转有如下特点：1．受力特点：在杆件两端垂直于杆轴线的平面内作用一对大小相等，方向相反的外力偶——扭转力偶。

其相应内力分量称为扭矩。

2．变形特点：横截面绕轴线发生相对转动，出现扭转变形。

若杆件横截面上只存在扭矩一个内力分量，则这种受力形式称为纯扭转。

§4-2 外力偶矩与扭矩的计算 扭矩图1．外力偶矩 m如图4-3所示的传动机构，通常外力偶矩不是直接给出的，而是通过轴所传递的功率mN和转速n 由下列关系计算得到的。

nN m 9550= (4-1a) 如轴在m 作用下匀速转动φ角，则力偶做功为φm A =，由功率定义ωφm dtd m dt dA N =⋅==。

角速度ω与转速n （单位为转/分，即r/min ）。

关系为60/2n πω=（单位为弧度/秒，rad/s ）。

由于1kW=1000N ·m/s ，N 千瓦的功率相当于每秒钟作功N W ×=1000，单位为N ·m ；而外力偶在1秒钟内所作的功为m n 2m W ⋅=⋅=πω/60 （N ·m ）由于二者作的功应该相等，则有m n N ⋅=×π21000/60由此便得（4-1）式。

式中：N —传递功率（千瓦，kW ） —转速（r/min ）n 如果传递功率单位是马力(PS)，由于1PS=735.5 N ·m/s ，则有nN m 7024=（N ·m ） (4-1b) 式中：N —传递功率（马力，PS ）n —转速（r/min ）2．扭矩T求出外力偶矩后，可进而用截面法求扭转内力——扭矩。

如图4-4所示圆轴，由m 0=∑x m ，从而可得A —A截面上扭矩T−m T ， m T =0=T 称为截面A —A 上的扭矩；扭矩的正负号规定为：按右手螺旋法则，T 矢量离开截面为正，指向截面为负。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
TSINGHUA UNIVERSITY
315
315
1116
486
解：1．确定控制面
A
B
1500
1500
315 Mx1=-315 n
C 2000
D
外加力偶处截面A、B 、C、D均为控制面。
2．应用截面法，由平衡方程
315
315 Mx2=-630
其中x轴平行于圆轴的
轴线，Mx轴垂直于圆轴
486 的轴线。将所求得的各
x
段的扭矩值，标在Mx－ x坐标系中，得到相应
的点，过这些点作x轴
的平行线，即得到所需
要的扭矩图。
第4章 圆轴扭转时的强度与刚度计算
TSINGHUA UNIVERSITY
剪应力互等定理
返回总目录
返回
第4章 圆轴扭转时的强度与刚度计算
dydzdx dxdzdy
x
第4章 圆轴扭转时的强度与刚度计算
剪应力互等定理 剪切胡克定律
TSINGHUA UNIVERSITY
y
dy dx
z
剪应力成对定理
在两个互相垂直的平
面上，剪应力必然成
对存在，且数值相等
，两者都垂直于两个
平面的交线，方向则
x 共同指向或共同背离 这一交线，这就是剪
Me P
P Me 9549 n [N m]
其中P为功率，单位为千瓦（kW）；n为轴的转 速，单位为转/分（r/min）。
如果功率P的单位用马力（1马力=735.5 N•m/s），则
Me
7024 P[马力] n[r / min]
[N m]
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
工程中承受扭转的圆轴
请判断哪些零件 将发生扭转？
TSINGHUA UNIVERSITY
传动轴
传动轴 将产生扭转
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴
请判断哪一杆件 将发生扭转？
第4章 圆轴扭转时的强度与刚度计算
TSINGHUA UNIVERSITY
工程中承受扭转的圆轴
返回总目录
返回
TSINGHUA UNIVERSITY
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴
请判断哪一杆件 将发生扭转？
当两只手用力相等 时，拧紧螺母的工 具杆将产生扭转。
第4章 圆轴扭转时的强度与刚度计算
材料力学
(4)
清华大学出版社
2020年8月4日
返回总目录
TSINGHUA UNIVERSITY
材料力学
上一章
基础篇之四
第4章 圆轴扭转时的强度 与刚度计算
返回 总目录
下一章
TSINGHUA UNIVERSITY
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴 外加扭力矩、扭矩与扭矩图 剪应力互等定理 剪切胡克定律 圆轴扭转时横截面上的剪应力分析 与强度设计 圆杆扭转时的变形及刚度条件 结论与讨论
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
TSINGHUA UNIVERSITY
例题 1
315
315
1116
486
A
B
C
D
1500
1500
2000
圆轴受有四个绕轴线转动的外加力偶，各力偶的力偶矩 的大小和方向均示于图中，其中力偶矩的单位为N.m， 尺寸单位为mm。
试 ：画出圆轴的扭矩图。
n
Mx 0
确定各段圆轴内的扭矩
486
Mx3=486 n
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
TSINGHUA UNIVERSITY
315
315
1116
486 3．建立Mx－x坐标系，
画出扭矩图
A
B
C
1500 1500
2000
Mx/N.m
486
O
315 315
630
630
D
建立Mx －x坐标系 ，
连接汽轮机和发 电机的传动轴将 产生扭转。
第4章 圆轴扭转时的强度与刚度计算
TSINGHUA UNIVERSITY
外加扭力矩、扭矩与扭矩图
返回总目录
返回
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
TSINGHUA UNIVERSITY
ቤተ መጻሕፍቲ ባይዱ
作用于构件的外扭矩与机器的转速、功率有关。
在传动轴计算中，通常给出传动功率P和转速n， 则传动轴所受的外加扭力矩Me可用下式计算：
外加扭力矩Me确定后，应用截面法可以确定横截面上的内 力——扭矩，圆轴两端受外加扭力矩Me作用时，横截面上 将产生分布剪应力，这些剪应力将组成对横截面中心的合 力矩,称为扭矩（twist moment），用Mx表示。
Me
Me
TSINGHUA UNIVERSITY
Me
Mx
n+
Mx
TSINGHUA UNIVERSITY
平衡方程+变形协调+物性关系
第4章 圆轴扭转时的强度与刚度计算
dz
应力成对定理（
pairing principle of
shear stresses）。
第4章 圆轴扭转时的强度与刚度计算
TSINGHUA UNIVERSITY
圆轴扭转时横截面上的 剪应力分析与强度设计
返回总目录
返回
TSINGHUA UNIVERSITY
第4章 圆轴扭转时的强度与刚度计算
圆轴扭转时横截面上的剪应力分析与强度设计
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
如果只在轴的两个端截面作用有外力偶矩，则沿 轴线方向所有横截面上的扭矩都是相同的，都等 于作用在轴上的外力偶矩。
当在轴的长度方向上有两个以上的外力偶矩作用 时，轴各段横截面上的扭矩将是不相等的，这时 需用截面法确定各段横截面上的扭矩。
扭矩沿杆轴线方向变化的图形，称为扭矩图 (diagram of torsion moment)。绘制扭矩图的方 法与绘制轴力图的方法相似。
应用平衡方法可以确定圆杆扭转时横截面上的内 力分量——扭矩，但是不能确定横截面上各点剪 应力的大小。这是圆截面扭转剪应力分布的超静 定性质。为了确定横截面上各点的剪应力，在确 定了扭矩后，还必须知道横截面上的剪应力是怎 样分布的。回顾超静定结构求解的“三部曲”:
l
2l
C
FA
A
FP
B
Me FB
Mx
n
Mx
剪应力互等定理 剪切胡克定律
y 微哪怎元些样能力才不互能能相平平衡衡？？
TSINGHUA UNIVERSITY
dy
dx
z
Me
x
dz Me
Me
Mx
n
Mx
第4章 圆轴扭转时的强度与刚度计算
剪应力互等定理 剪切胡克定律
y 怎样才能平衡？
TSINGHUA UNIVERSITY
dy dz
dx
z
根据力偶平衡理论