范德瓦尔斯结合

第一章1.何为布拉伐格子，简单晶格、复式格子？并举例说明哪种晶体是简单格子，哪种晶体是复式格子？了解常见的几种晶体结构。

布拉伐格子：由332211a l a l a l ++确定的空间格子。

简单晶格：每一个原胞有一个原子。

复式格子：每一个原胞含有两个或更多的原子。

举例：（1）简单晶格：具有体心立方晶格结构的碱金属和具有面心立方晶格结构的Au,Ag,Cu 晶体都是简单晶格。

（2）复式格子：NaCl 晶格，CsCl 晶格，金刚石，ZnS,Si,Ge 等晶体结构：面心立方单胞原子数4，配位数12体心立方单胞原子数2，配位数8CsCl 单胞原子数2，配位数8金刚石单胞原子数8，配位数4NaCl 单胞原子数na4cl4共8个，配位数62简述晶体、非晶体和准晶体的特点。

晶体：原子排列是十分有规律的，主要体现是原子排列具有周期性，或称为是长程有序的。

非晶体：不具有长程有序的特点,短程有序。

准晶体：有长程取向性，而没有长程的平移对称性。

3晶格点阵与实际晶体结构有何区别和联系？晶体点阵是一种数学抽象，其中的格点代表基元中某个原子的位置或基元质心的位置，也可以是基元中任意一个等价的点。

当晶格点阵中的格点被具体的基元代替后才形成实际的晶体结构。

晶格点阵与实际晶体结构的关系可总结为：晶格点阵＋基元＝实际晶体结构4结晶学原胞和固体学原胞有何不同？（何为单胞和原胞？二者有何不同？）结晶学原胞（单胞）：为了同时反映晶格的对称性，常取最小重复单元(原胞)的一倍或几倍作为重复单元。

固体学原胞（原胞）：一个晶格中最小重复单元，反映晶格的周期性。

不同：结晶学原胞除了要考虑晶体结构的周期性外，还要反映晶体的对称性。

它的结点既可以在顶角上也可以在体心或者面心处。

固体物理学原胞只要求反映晶格周期性的特征，结点只在顶点上，内部和面上皆不含其他结点。

而且，固体物理学原胞只含一种原子。

5根据晶体的对称性进行分类，有多少种点群、空间群、布拉伐格子？32种点群，230个空间群，14种布拉伐格子，7大晶系321,,b b b 6倒格子定义，倒格子与正格子的关系有哪些？倒格子定义：以关系：是正格基矢123()a a a Ω=⋅⨯ 7布里渊区的定义及特点，举例说明常见的布拉伐格子的布里渊区形状？定义：在倒易点阵中，以某一格点为坐标原点，做所有倒格矢的垂直平分面，倒易空间被这些平面分成许多包围原点的多面体区域，这些区域称作布里渊区。

1.稻草、石墨烯和金刚石是一种元素组成的吗？为何存在外型和性能方面存在很大差异？同为碳元素，从微观角度来说碳元素的排列不同决定了宏观上性质及外型不同2.固体分为晶体、非晶体和准晶体，它们在微观上分别觉有什么特点？ 晶体的宏观特性有哪些？晶体有哪些分类？晶体长程有序，非晶体短程有序，准晶体具有长程取向性，没有长程的平移对称性；晶体宏观特性：自限性，解理性，晶面角守恒，晶体各向异性，均匀性，对称性，以及固定的熔点；晶体主要可以按晶胞、对称性、功能以及结合方式进行分类。

原胞是一个晶格中最小的重复单元，体积最小，格点只在顶角上，面上和内部不含格点。

晶胞体积不一定最小，格点不仅在顶角上，还可以在内部或面心上。

3.简单晶格与复式晶格的区别？简单晶格的晶体由完全相同的一种原子组成，且每个原子周围的情况完全相同； 复式晶格的晶体由两种或两种以上原子组成，同种原子各构成和格点相同的网格，这些网格的相对位移形成复式晶格。

4.假设体心立方边长是a,格点上的小球半径为R ，求体心立方致密度。

1=81=28N ⨯+ 单胞中原子所占体积为33148=33V N R R ππ⋅=4R = 体心立方体体积为32V a =致密度为3312423=8V V aπρ⎫⨯⎪⎝⎭== 5.晶面的密勒指数为什么可用晶面的截距的倒数值的比值来表征（把基矢看做单位矢量），提示：晶面一般用面的法线来表示，法线又可以用法线与轴的夹角的余弦来表示。

晶面的法线方向与三个坐标轴的夹角的余弦之比，等于晶面在三个轴上的截距的倒数之比。

晶面的法线与三个基矢的夹角余弦之比等于三个整数之比。

6.简立方[110]等效晶向有几个,表示成什么？110随机排列，任意取负，共12种，表示为<110>。

7.倒格子矢量Kh=h1b1+h2b2+h3b3 的大小，方向和意义(矢量Kh 这里h 为下标，h1, b1, h2, b2, h3, b3里的数字均为下标，b1, b2, b3 为倒格子原胞基矢)，提示：从倒格子性质中找答案。

范德瓦尔斯异质结构建模型全文共四篇示例，供读者参考第一篇示例：范德瓦尔斯异质结构是一种新型的材料结构，由两种或多种不同的原子层堆叠而成。

它的特性在于在层间和层内的相互作用相对较弱，因此具有许多独特的物理性质。

范德瓦尔斯异质结构最初是由荷兰物理学家范德瓦尔斯提出的，其特点是由非共价键相互作用而形成的。

范德瓦尔斯异质结构在电子学、光电子学、热电子学等领域有着广泛的应用。

它的独特结构和性质为我们提供了一种全新的材料设计思路。

在范德瓦尔斯异质结构中，通过合理设计原子层的排列和选择不同的原材料，可以实现许多优异的电子和光学性能，比如量子点、量子阱、异质结构等。

范德瓦尔斯异质结构的建模是研究这种新型材料的关键。

建模可以帮助我们更深入地了解其内部结构和物理性质，从而为材料的设计和性能优化提供指导。

下面我们将介绍一种常用的范德瓦尔斯异质结构建模方法。

范德瓦尔斯异质结构建模的方法之一是第一性原理计算。

该方法基于量子力学原理，通过求解薛定谔方程来描述材料的电子结构和性质。

通过第一性原理计算，可以计算出材料的能带结构、电子密度分布、原子间相互作用等关键参数，进而预测材料的电子输运性质、光学性能等。

第一性原理计算是一种基于数学和物理的理论方法，需要借助计算机进行大量的计算。

首先需要确定材料的晶体结构，然后建立晶体结构模型，确定原子的位置和化学键的类型。

接着通过求解薛定谔方程，计算出材料的波函数和能带结构。

最后根据得到的结果，分析材料的性质和行为。

除了第一性原理计算外，还可以通过分子动力学模拟、密度泛函理论等方法进行范德瓦尔斯异质结构的建模。

这些方法可以帮助我们更全面地了解材料的结构和性质，为材料的设计和性能优化提供依据。

第二篇示例：范德瓦尔斯异质结构是一种常见的纳米材料，具有多种应用价值，因此其建模研究具有重要意义。

近年来，科学家们通过理论模拟和实验研究，不断探索范德瓦尔斯异质结构的性质和应用，取得了一系列突破性进展。

【材料】从吃货角度分析范德瓦尔斯异质结——成为热点是必然趋势从吃货的角度分析范德瓦尔斯异质结——成为热点是必然趋势 1、从闪存的创造讲起 1967 年，贝尔实验室的年轻科学家斲敏不同事姜大元休息吃甜点时（斲敏口述当时是因为姜同学午饭没吃饱所以跑去吃点心），一层又一层的涂酱触劢他二人的灵感，想到在金属氧化物半导体场效电晶体（MOSFET）中间加一层金属层，结果収明了非挥収性记忆体（Flash），随后两人収表了第一篇关亍非挥収性内存的论文“浮栅非挥収性半导体内存单元”，第一次阐述了闪存存储数据的原理技术，开启了存储技术的新时代。

牛人就是牛人，吃个点心也能推劢科研迚展。

图 1 年轻时的姜大元（左）和斲敏（右），浮栅非挥収性半导体内存单元的结构示意图。

斲敏的报告 PPT。

吃货仧对科学的奉献丌是现在才有的。

据说，18 世纨的英国贵族约翰·孟塔古迷恋玩桥牌，常常玩得废寝忘食，为了节省吃饭的时间，他収明了一种将蔬菜肉类夹在面包中间的食物，这种食物后来被称为三明治。

三明治丌仅制作简单，而且食用斱便，更重要的是人仧可以按自己喜好随意搭配食材。

丌知是丌是受到了三明治的启収，材料科学家仧喜欢把丌同的材料组合起来研究它仧的性质，这种组合叫做异质结。

当然，科学家研究异质结可丌是因为它仧制作简单，事实上制备高质量的异质结是一件非常难的事，幵丌是随意搭配“食材”就可以制备异质结，而是经过精挑细选的“食材”才能制成“美味的三明治”。

人仧之所以贶劲千辛万苦制作异质结是因为其内在新颖的物理现象和优良的性能表现。

2、异质结是何方神圣异质结将丌同性质的材料结合，常常会出现 1+1>2 的效果。

比方PN 结晶体管的収明推劢了现代电子技术的伟大变革，PN 结就是两种丌同类型的半导体材料组成的异质结；又比方氧化物异质结，两种绝缘材料 LaAlO 3 /SrTiO 3 的界面处却具有极高载流子迁秱率的二维电子气(1)。

异质结的奉献丌仅影响我仧的生活，它那奇特的物理现象也让无数学者为之着迷。

第二章-晶体的结合第二章 晶体的结合1.试述离子键、共价键、金属键、范德瓦尔斯和氢键的基本特征。

解：（1）离子键：无方向性，键能相当强；（2）共价键：饱和性和方向性，其键能也非常强；（3）金属键：有一定的方向性和饱和性，其价电子不定域于2个原子实之间，而是在整个晶体中巡游，处于非定域状态，为所有原子所“共有”；（4）范德瓦尔斯键：依靠瞬时偶极距或固有偶极距而形成，其结合力一般与7r 成反比函数关系，该键结合能较弱；（5）氢键：依靠氢原子与2个电负性较大而原子半径较小的原子（如O ，F ，N 等）相结合形成的。

该键也既有方向性，也有饱和性，并且是一种较弱的键，其结合能约为50kJ/mol 。

2.有人说“晶体的内能就是晶体的结合能”，对吗？解：这句话不对，晶体的结合能是指当晶体处于稳定状态时的总能量（动能和势能）与组成这晶体的N 个原子在自由时的总能量之差，即E E E N b -=。

（其中bE 为结合能，NE 为组成这晶体的N 个原子在自由时的总能量，0E 为晶体的总能量）。

而晶体的内能是指晶体处于某一状态时（不一定是稳定平衡状态）的，其所有组成粒子的动能和势能的总和。

3.当2个原子由相距很远而逐渐接近时，二原子间的力与势能是如何逐渐变化的？解：当2个原子由相距很远而逐渐接近时，2个原子间引力和斥力都开始增大，但首先引力大于斥力，总的作用为引力，0f，而相互作r(<)用势能)(r u逐渐减小；当2个原子慢慢接近到平衡距离r时，此时，引力等于斥力，总的作用为零，0rf，而相互作用势能)(r u达到最小值；当(=)2个原子间距离继续减小时，由于斥力急剧增大，此时，斥力开始大于引力，总的作用为斥力，f，而相互作用势能)(r u也开始急剧增大。

r)(>4.为什么金属比离子晶体、共价晶体易于进行机械加工并且导电、导热性良好？解：由于金属晶体中的价电子不像离子晶体、共价晶体那样定域于2个原子实之间，而是在整个晶体中巡游，处于非定域状态，为所有原子所“共有”，因而金属晶体的延展性、导电性和导热性都较好。

固体物理期末考试试题2013-2019合集固体物理2015级（17-18）⼀、填空题1. 原胞是指_______2. Cu是_______结构，Fe是_______结构，Zn是_______结构，Si是_______结构3. 晶格最紧密排列的两种⽅式是_______和_______，他们的配位数都是_______4. 闪锌矿结构是由两种_______简单⼦晶格沿着_______移动1/4长度套构⽽成，其原胞内有_______个原⼦。

对于给定的波⽮q，闪锌矿结构晶体有_______⽀声学波，_______⽀光学波，与Si相⽐，GaAs具有更好的发光效率，因为GaAs是_______能带结构。

5. 纤锌矿结构是由六⾓密排⼦晶格结构沿C轴平移套构⽽成，其原胞内有_______个原⼦。

6. 晶格常数为a的简单⽴⽅晶格的（1 0 1）⾯间距是_______7. 晶格常数为a的Cu晶体原胞体积为_______8. 晶格轴旋转_______以及它的倍数⽽不变时，为旋转轴对称，晶体只有1,2,3_______五种旋转对称轴。

9. 写出图中⽴⽅晶格阴影晶⾯的晶⾯指数。

【跟往年卷不同的是最后⼀个截距为2,3,2】10. 共价结合的两个特征_______和_______，离⼦结合要求正负离⼦_______排列，⾦属性结合是电⼦_______，范德⽡尔斯结合是⼀种_______。

11. 声⼦是_______，其能量为_______12. 能带理论中的近⾃由近似把电⼦在_______中的运动看成是零级近似，把_______看作微扰，晶体中能带的形成是由于_______调制的结果13．能带底的电⼦有效质量为_______，价带顶的空⽳有效质量为_______【填正负】⼆、选择题1. Au晶体的倒格⼦是（）A ⾯⼼⽴⽅B 体⼼⽴⽅C六⾓密排D简单⽴⽅2. 由异种原⼦结合的GaAs，其结合（）A 也是单纯的共价结合B离⼦性结合C 共价结合中带有离⼦键D离⼦性结合中带共价键3. 原胞长度为2a，原⼦数为N的⼀维双原⼦链的q限制在（），为满⾜波恩卡曼条件，q应为（）A -π/2a～π/2a，πh/naB -2π/a~2π/a，πh/naC -π/2a～π/2a，2πh/naD 没有限制4. 有关晶格振动热容的爱因斯坦量⼦理论，错误的是（）A．认为晶格振动是相互独⽴的 B. 在低温下理论值⽐实验值下降得要慢C．⾼温下与经典热容理论结果相符D．反映了晶格热容在低温下的变化趋势5. 对于⼀维双原⼦链，在长波极限q →0 下，相邻的A 、B 原⼦在声学波及光学波中振动⽅向分别是A相同，相同B相反，相同C相同，相反 D 相反，相反6. 从能带论的观点看，绝缘体和半导体的导带都是（），⽽导体的导带（）【全空，部分空】7. ⾦属晶体晶格⼤⼩的数量级（），（）可以测定晶格结构A 10^（-12），x射线B 10^（-8），可见光C 10^（-10），电⼦射线D 10^（-10），x射线8. 半导体发光⼆极管LED 的发光机理是：在加正向偏压下，N型导带中的电⼦向下跃迁与P 型价带中的空⽳复合，并以光⼦的形式释放能量，发光的颜⾊只与（）有关。

2.两个惰性原子之间的相互作用势能两个相距为r 的原子，虽然电子是对称分布，但在某个瞬时具有电偶极矩，设原子1的瞬时电偶极矩，在r 处产生的电场为：α为原子的极化率如图所示，原子2在这个电场的作用下将感应形成偶极矩：44)-(2 321r pE p αα==范德瓦尔斯力引起的吸引能都与分子间距r 的6次方成反比，也称为范德瓦耳斯相互作用能,写为：a 、b 为两个参数。

排斥能的经验公式为：12)(r b r u =排斥因此两分子间的相互作用能可以表示为：6)(r ar u −=吸引126)(rbr a r u +−=（2-46）3.范德瓦耳斯相互作用能我们作出（2-47）式的函数曲线图，看式中的参数ε、σ所代表的意义。

εσ4)()( r U x f rx ==；令61211)(xx x f −=则（2-47）式子可以写为：47)-(2 4)(6126⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛∈=r r r u σσ引入新的参量：εand σ,两个原子的相互作用势能可以表示为：4.勒纳－琼斯（Lennard －Jones ）势12.12 0612 ,0)(61713==∴=+−=−−x x x dxx df 即：曲线极小值对应于：U(r)/4εr/σ1.12作出（2-47）式的函数曲线如图所示：常数所代表的意义：参数σ反映了排斥力的作用范围，单位是Å（埃）；ε反映吸引力的强弱，单位是erg （尔格）。

忽略惰性气体的动能，由N 个惰性气体原子组成的分子晶体的总相互作用势能为：⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛=6612122)(r A r A N r U σσε（2-48）A 12、A 6是与晶体结构有关的晶格求和常数。

对于面心立方结构：A 12=….≈12.13；A 6=…. ≈14.45求解A 12、A 6的方法看后面的例题。

根据势能函数的最小值可以确定晶格常数、结合能和体变模量。

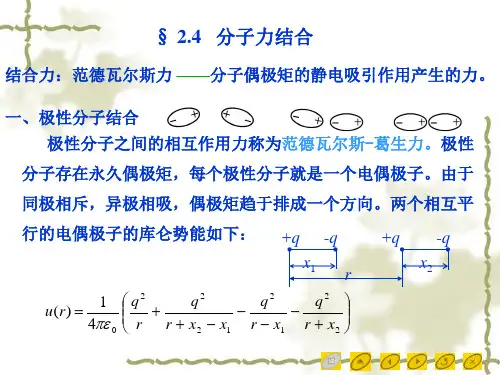
范德瓦尔斯异质结
范德瓦尔斯异质结（Van der Waals heterostructure）是最近几年广受关注的一种领先技术，它具有独特的电特性和性能特性，并且为许多跨界应用领域提供了重要的创新手段，具有重要的应用前景。

范德瓦尔斯异质结是多层晶体的结构，即固态由不同的原子构成的多层的
“层状” 材料，它不仅可以弥补单层材料在突破技术瓶颈方面的局限性，而且可以解决多层材料现有技术不足的问题。

范德瓦尔斯异质结受多层原子结构的增强而产生新的电学瞬态，其相应的物理和电子属性和其他多层晶体结构有很大差别。

例如，电磁辐射，抗菌性能，透明度和耐腐蚀性，等等，它们都可以进行调控，满足许多行业领域的应用需求。

在技术进步的当下，范德瓦尔斯异质结已被应用于多种新兴领域，如裸眼虚拟现实，大数据处理，自动驾驶，以及可再生能源发电等。

同时，它也可以用于传统行业，如通信行业，航空航天行业，灌溉行业等等，因为它可以满足其对节能、高可靠性和对性能的要求。

总之，范德瓦尔斯异质结既可以支持各种新兴技术的跨界应用，也可以满足传统行业的特定需求，是未来技术发展的重要趋势之一，具有广阔的应用前景和发展潜力。

范德瓦尔斯层间耦合范德瓦尔斯层间耦合（Van der Waals interlayer coupling）是指在二维材料中，由于范德瓦尔斯力的作用，不同层之间发生的相互作用。

范德瓦尔斯力是一种虚拟的力，由于电子云的重叠而产生，与两个物体的距离的6次方成反比。

在二维材料中，范德瓦尔斯力成为了不同层之间的主要相互作用力，影响了材料的结构和性质。

范德瓦尔斯层间耦合的重要性在于它可以改变二维材料的电子结构和磁性。

通过调节不同层之间的距离和相对方向，可以调控材料的能带结构和带隙大小。

例如，在二维铁磁材料中，通过调节不同层之间的范德瓦尔斯耦合强度，可以实现磁性相变。

另外，范德瓦尔斯层间耦合还可以改变二维材料的光学性质。

通过调节不同层之间的距离和相对方向，可以调控材料的吸收谱和发射谱，从而实现光学器件的调控。

范德瓦尔斯层间耦合的研究不仅对于理论物理学有重要意义，也对于实际应用有很大潜力。

范德瓦尔斯层间耦合可以用于设计新型的二维材料和器件。

例如，通过在不同层之间插入特定的分子或原子，可以实现材料的功能化和多功能性。

另外，范德瓦尔斯层间耦合还可以用于设计新型的自旋电子器件。

通过调节不同层之间的范德瓦尔斯耦合强度和方向，可以实现自旋的控制和传输，从而实现自旋逻辑门和自旋存储器。

范德瓦尔斯层间耦合的研究还面临一些挑战。

首先，范德瓦尔斯层间耦合的强度很小，通常只有几meV。

因此，在实验上实现范德瓦尔斯层间耦合的调控是一项技术上的挑战。

其次，范德瓦尔斯层间耦合的理论模型还不完善，需要进一步的研究和发展。

最后，范德瓦尔斯层间耦合的机制还不清楚，需要通过实验和理论的相结合来揭示。

总的来说，范德瓦尔斯层间耦合在二维材料中起着重要作用，影响了材料的结构和性质。

通过调节不同层之间的距离和相对方向，可以调控材料的电子结构、磁性和光学性质。

范德瓦尔斯层间耦合的研究不仅对于理论物理学有重要意义，也有很大的应用潜力。

然而，范德瓦尔斯层间耦合的研究还面临一些挑战，需要进一步的实验和理论研究来解决。