2.3-范德瓦尔斯结合、晶体结合的规律性
- 格式:ppt
- 大小:1.02 MB
- 文档页数:25




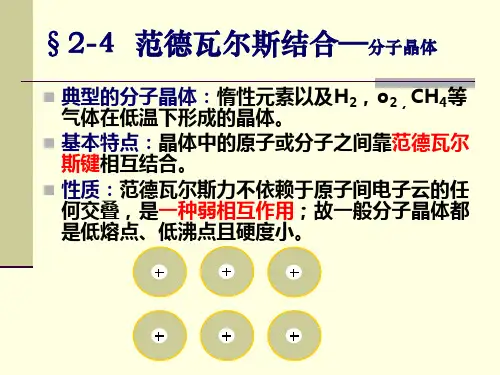
范德瓦尔斯力的动力学机制范德瓦尔斯力的动力学机制范德瓦尔斯力是存在于中性分子或原子之间的一种弱的电性吸引力。
它是分子间相互结合的主要原因,并且其中的色散力是惰性气体在低温下能液化甚至固化的重要原因。
下面是我从网上及资料和文献中查到的一些关于范德瓦尔斯力的动力学机制的资料。
范德瓦尔斯力的主要来源有三种作用机制:(1)、极性分子具有永久的电偶极矩,通常这些偶极矩杂乱无章地排列,因而极性分子是电中性的,但在极性分子晶体中这些偶极矩呈现规则排列,极性分子之间就会产生静电吸引力,称为葛生力又称“取向力”,它的大小与分子的极性变形性温度有关。
极性分子的偶极矩愈大,取向力愈大;温度愈高,取向力愈小。
(2)、无极分子中正负电荷系的中心重合,分子不具有电偶极矩,但当极性分子靠近它时,可使正、负电荷分开,产生诱导电偶极矩,从而在极性分子和无极性分子之间产生吸引力,称诱导力或德拜力。
(3)、一对非极性分子本身由于电子的概率运动,可以相互配合产生一对方向相反的瞬时偶极矩,这一对瞬时偶极矩相互作用,称为“色散力”。
这种机制是范德华力的主要来源,1930年由F.W.伦敦首先根据量子力学原理给出解释,因此也称为“伦敦力”。
对于上述三中机制共性是:永远存在于分子之间,属于是近程力且力的作用很小.无方向性和饱和性. 经常是色散力为主。
简单起见,将上述色散作用势推导出来:用带点粒子的线性谐振子代表瞬时偶极矩,r 为两个谐振子平衡点(正电荷所处的位置)之间的距离,1x 与2x 为带负电荷的质点在震动过程中离开平衡点的瞬时位移。
这两个振子的能量分别为21212121121212121kx p m kx mv E +=+= 22222222221212121kx p m kx mv E +=+=其中k 为振子的力常数,1p 与2p 为它们的动量。
当r 很大时,两振子间无相互作用力,系统的总能量为21E E +,此时振子的震动频率为mk πν210=;但当r 不很大时,振子间的相互作用能为⎥⎦⎤⎢⎣⎡+---+-+=21212012111141x r x r x x r r e u πε 当1x r >>、2x 时,上式可以展开并只取第一项而略去高次小的项,则系统的总能量可以写为1221u E E E ++=()3021222212221222r x x e x x k m p p πε-+++= 由于电场E 的作用,使振子产生一位移x ,且kx E =,k 为恢复常数。
2.两个惰性原子之间的相互作用势能两个相距为r 的原子,虽然电子是对称分布,但在某个瞬时具有电偶极矩,设原子1的瞬时电偶极矩,在r 处产生的电场为:α为原子的极化率如图所示,原子2在这个电场的作用下将感应形成偶极矩:44)-(2 321r pE p αα==范德瓦尔斯力引起的吸引能都与分子间距r 的6次方成反比,也称为范德瓦耳斯相互作用能,写为:a 、b 为两个参数。
排斥能的经验公式为:12)(r b r u =排斥因此两分子间的相互作用能可以表示为:6)(r ar u −=吸引126)(rbr a r u +−=(2-46)3.范德瓦耳斯相互作用能我们作出(2-47)式的函数曲线图,看式中的参数ε、σ所代表的意义。
εσ4)()( r U x f rx ==;令61211)(xx x f −=则(2-47)式子可以写为:47)-(2 4)(6126⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛∈=r r r u σσ引入新的参量:εand σ,两个原子的相互作用势能可以表示为:4.勒纳-琼斯(Lennard -Jones )势12.12 0612 ,0)(61713==∴=+−=−−x x x dxx df 即:曲线极小值对应于:U(r)/4εr/σ1.12作出(2-47)式的函数曲线如图所示:常数所代表的意义:参数σ反映了排斥力的作用范围,单位是Å(埃);ε反映吸引力的强弱,单位是erg (尔格)。
忽略惰性气体的动能,由N 个惰性气体原子组成的分子晶体的总相互作用势能为:⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛=6612122)(r A r A N r U σσε(2-48)A 12、A 6是与晶体结构有关的晶格求和常数。
对于面心立方结构:A 12=….≈12.13;A 6=…. ≈14.45求解A 12、A 6的方法看后面的例题。
根据势能函数的最小值可以确定晶格常数、结合能和体变模量。
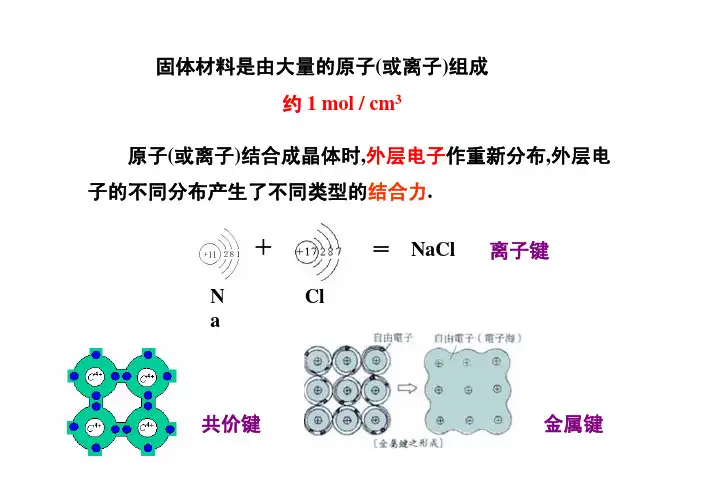
固体材料是由大量的原子(或离子)组成约1 mol / cm 3原子(或离子)结合成晶体时,外层电子作重新分布,外层电子的不同分布产生了不同类型的结合力.Na Cl +=NaCl 离子键共价键金属键结合力类型决定了晶体的微观结构乃至宏观物理性质.本章主要介绍不同结合类型中原子间相互作用与晶体内能、晶体的微观结构和宏观物理性质之间的联系.共价键结合(金刚石)--原子间束缚非常强,导电性差金属键结合(金属Cu )--对电子束缚较弱,良导体——原子的电子分布核外电子的分布遵从泡利不相容原理、能量最低原理和洪特规则.能量最低原理电子在原子核外排布时,要尽可能使电子的能量最低1s、2s、2p、3s、3p、4s、3d、4p、4d……泡利不相容原理每一轨道中只能客纳自旋相反的两个电子.洪特规则电子在原子核外排布时,将尽可能分占不同的轨道,且自旋平行——原子的电子分布_----电离能_----电离能_----电离能_----电子亲和能_----原子电负性_----原子电负性2.Pauling鲍林提出的电负性计算方法(较通用):_----原子电负性•横向•电离能•亲和能•电负性按结合力的性质和特点,晶体可分为5种类型:离子晶体(离子结合)共价晶体(共价结合)金属晶体(金属结合)氢键晶体(氢键结合)如何理解各种晶体呢?离子晶体:正离子与负离子的吸引力就是库仑力.共价结合:靠近的两个电负性大的原子各出一个电子形成电子共享的形式.金属结合:原子实依靠原子实与电子云间的库仑力紧紧地吸引着.氢键结合:氢先与电负性大的原子形成共价结合后, 氢核与负电中心不在重合, 迫使它通过库仑力再与另一个电负性大的原子结合.分子结合:电偶极矩把原本分离的原子结合成了晶体. 电偶极矩的作用力实际就是库仑力.可见, 所有晶体结合类型都与库仑力有关.原子间相互作用势能----结合力的共性吸引力排斥力库仑引力库仑斥力泡利原理引起(1)吸引力和排斥力都是原子间距离r 的函数.注:(2)吸引力是长程力,排斥力短程力.(3)当r =r 0时, 原子间合力为零, 原子处于平衡.类比于弹簧振子()()⎟⎠⎞⎜⎝⎛−−=−=++11n m r nB r mA dr r du r f 为什么排斥力是短程力?()()()B A r u r u r u +−=+=()()⎜⎛−−=−=nB mA r du r f设晶体中第i个原子与第j个原子之间的相互作用势能u(r)为ij()()∑∑∑==NNNr u r u U 1晶体的结合能:()()∑=N r u Nr u晶格常数由于晶格具有周期性,设临近两原子间距R,则晶体体积可写成体弹性模量单位压强引起的体积的相对变化率。
第一章原子结构与结合键电离能:基态原子失去最外层的一个电子所需的能量。
电子亲和能: 基态中性原子获得一个电子成为负离子所释放出的能量。
电负性:代表原子获得电子的能力,这个电子是元素原子自身以外的电子,而这种能力决定于原子结构。
离子键:原子间通过电子转移产生正离子和负离子,两者相互吸引所形成的化学键称为离子键共价键:两个或多个原子共同使用它们的外层电子,在理想情况下达到电子饱和的状态,由此组成比较稳定的化学结构叫做共价键金属键:由自由电子及排列成晶格状的金属离子之间的静电吸引力组合而成。
范德瓦尔斯键:一个分子中的带正电部分会吸引另一个分子中的带负电部分,这种结合力称为范德瓦尔斯键。
极化:分子中共价电子的非对称分布,使分子的某一部分比其他部分更偏于带正电或带负电的现象。
第二章晶体结构晶体:物质的基元在三维空间呈有规律的周期性重复排列所形成的物质。
长程有序:原子在三维空间呈有规律的周期性重复。
各向异性:材料的物理,化学或力学性能随方向的不同表现出一定差异的特性。
结点:为了便于分析晶体的周期性排列规律,将一个或一组刚性球抽象成一个点,这些点称为结点。
基元:被抽象的一个或一组原子。
空间点阵:结点在三维空间作周期性排列所形成的三位阵列。
晶格:为了便于描述空间点阵的模型,用3套平行的直线将所有结点连接起来,所形成的三维空间格架。
晶胞:从晶格中抽取具有代表性的基础单元。
点阵常数(晶格常数):以晶胞角上的某一结点为原点,以该晶胞上过原点的三个棱边为坐标轴x,y,z,则晶胞的形状和大小即可由这三条棱边a,b,c和棱边夹角α、β、γ这六个点阵参数来表示。
布拉维点阵:根据每个结点的周围环境相同,用数学分析方法证明晶体中的空间点阵只有14种。
晶向:空间点阵中各结点列的方向代表晶体中原子排列的方向。
晶面:空间点阵中任意一组阵点的平面代表晶体中的原子平面。
晶向指数:晶列通过轴矢坐标系原点的直线上任取一格点,把该格点指数化为互质整数,称为晶向指数,表示为[h,k,l]。