范德瓦耳斯气体的热力学性质3
- 格式:doc
- 大小:175.50 KB
- 文档页数:8


对范德瓦耳斯气体的热力学函数及热容量的研究范德瓦耳斯气体是一种理想气体的延伸,它在描述实际气体的热力学性质方面更准确。
本文将对范德瓦耳斯气体的热力学函数及热容量进行研究,并探讨范德瓦耳斯方程的应用。
1.范德瓦耳斯气体的热力学函数:范德瓦耳斯气体可以用以下方程描述:P(V-b)=nRT其中,P为气体的压强,V为气体的体积,n为气体的物质的量,R为气体常数,T为气体的温度,b为修正系数。
从这个方程中可以得到范德瓦耳斯气体的热力学函数。
首先,我们可以计算出范德瓦耳斯方程的状态方程:PV=nRT/(V-b)然后,根据理想气体的状态方程,可以知道热力学函数U与范德瓦耳斯方程的关系:dU = C_vdT = TdS - PdV其中,C_v为定容热容量,T为温度,S为熵,dU表示内能的微分。
将前面推导的范德瓦耳斯方程代入上述等式,可以得到范德瓦耳斯气体的热力学函数:dU = C_vdT = TdS - (nRT)/(V - b)dV2.范德瓦耳斯气体的热容量:根据上一节的推导,范德瓦耳斯气体的定容热容量C_v可以表示为:C_v=T(∂S/∂T)V现在来计算这个偏导数。
假设范德瓦耳斯气体满足简单的状态方程:P = nkT其中,k为玻尔兹曼常数。
由于S与V无关,我们可以得到:dS=(∂S/∂T)VdT将以上两式代入定容热容量的表达式中:C_v = T(dS/dT)V = T(1/T)kndT从而可以化简为:C_v = kn即范德瓦耳斯气体的定容热容量与物质的量成正比。
3.范德瓦耳斯方程的应用:范德瓦耳斯方程可以广泛应用于研究气体的行为和性质,特别是高压下的气体。
它可以用于计算气体的物质的量、压强、温度和体积之间的关系。
通过范德瓦耳斯方程,我们可以定量地描述气体的压力、体积和温度之间的关系。
例如,在常温常压下,我们可以计算气体的物质的量。
另外,范德瓦耳斯方程还可以用于计算气体的体积在不同压力和温度下的变化。
总结:本文对范德瓦耳斯气体的热力学函数及热容量进行了研究。

理想气体的热力学性质1. 引言理想气体是一个重要的物理模型,用于描述宏观气体现象。
在理想气体模型中,气体分子被假设为没有体积、相互之间没有相互作用力,并且遵循分子运动论的统计规律。
理想气体的热力学性质是描述其在不同温度、压强等条件下的宏观行为。
本章将介绍理想气体的热力学性质,包括状态方程、等温过程、绝热过程、等压过程和热力学第一定律等。
2. 状态方程理想气体的状态方程是描述其状态(温度、压强、体积)之间关系的方程。
最常用的状态方程是范德瓦尔斯方程,它修正了理想气体状态方程中未考虑分子间相互作用力的缺陷。
范德瓦尔斯方程为:( p + )(V_m - b) = RT其中,( p ) 是气体的压强,( V_m ) 是气体的摩尔体积,( R ) 是理想气体常数,( T ) 是气体的绝对温度,( a ) 和 ( b ) 是范德瓦尔斯方程的参数,分别表示气体分子间的吸引力和分子的体积。
3. 等温过程等温过程是指气体在过程中温度保持不变的过程。
在等温过程中,气体的压强和体积之间遵循玻意耳-马略特定律:其中,( k ) 是一个常数。
等温过程的特点是气体分子平均动能不变,因此等温过程是可逆的。
4. 绝热过程绝热过程是指气体在过程中没有热量交换的过程。
在绝热过程中,气体的内能保持不变。
根据热力学第一定律,绝热过程中的功等于内能的变化。
当气体经历等压绝热过程(如等压膨胀或等压压缩)时,其温度发生变化,遵循盖-吕萨克定律:=其中,( V_1 ) 和 ( V_2 ) 是气体在两个状态下的体积,( T_1 ) 和 ( T_2 ) 是气体在两个状态下的绝对温度。
当气体经历等容绝热过程(如等容膨胀或等容压缩)时,其温度变化遵循查理定律:=其中,( p_1 ) 和 ( p_2 ) 是气体在两个状态下的压强,( T_1 ) 和 ( T_2 ) 是气体在两个状态下的绝对温度。
5. 等压过程等压过程是指气体在过程中压强保持不变的过程。




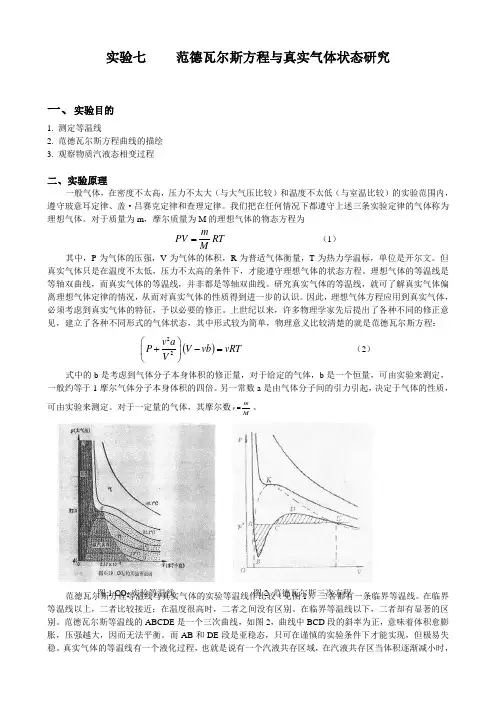
实验七范德瓦尔斯方程与真实气体状态研究一、实验目的1. 测定等温线2. 范德瓦尔斯方程曲线的描绘3. 观察物质汽液态相变过程二、实验原理一般气体,在密度不太高,压力不太大(与大气压比较)和温度不太低(与室温比较)的实验范围内,遵守玻意耳定律、盖·吕赛克定律和查理定律。
我们把在任何情况下都遵守上述三条实验定律的气体称为理想气体。
对于质量为m ,摩尔质量为M 的理想气体的物态方程为m PV RT M= (1) 其中,P 为气体的压强,V 为气体的体积,R 为普适气体衡量,T 为热力学温标,单位是开尔文。
但真实气体只是在温度不太低,压力不太高的条件下,才能遵守理想气体的状态方程。
理想气体的等温线是等轴双曲线,而真实气体的等温线,并非都是等轴双曲线。
研究真实气体的等温线,就可了解真实气体偏离理想气体定律的情况,从而对真实气体的性质得到进一步的认识。
因此,理想气体方程应用到真实气体,必须考虑到真实气体的特征,予以必要的修正。
上世纪以来,许多物理学家先后提出了各种不同的修正意见,建立了各种不同形式的气体状态,其中形式较为简单,物理意义比较清楚的就是范德瓦尔斯方程:()22v a P V vb vRT V ⎛⎫+-= ⎪⎝⎭ (2) 式中的b 是考虑到气体分子本身体积的修正量,对于给定的气体,b 是一个恒量,可由实验来测定,一般约等于1摩尔气体分子本身体积的四倍。
另一常数a 是由气体分子间的引力引起,决定于气体的性质,可由实验来测定。
对于一定量的气体,其摩尔数M mv =。
范德瓦尔斯方程等温线与真实气体的实验等温线作比较(见图1),二者都有一条临界等温线。
在临界等温线以上,二者比较接近;在温度很高时,二者之间没有区别。
在临界等温线以下,二者却有显著的区别。
范德瓦尔斯等温线的ABCDE 是一个三次曲线,如图2,曲线中BCD 段的斜率为正,意味着体积愈膨胀,压强越大,因而无法平衡。
而AB 和DE 段是亚稳态,只可在谨慎的实验条件下才能实现,但极易失图1 CO 2实验等温线 图2 范德瓦尔斯三次方程稳。

范德瓦耳斯气体的热力学性质陈东2008061144(黔南民族师范学院物理与电子科学系,贵州都匀 558000)【摘要】讨论范德瓦尔斯气体的内能、熵、焓和自由能,给出相应的数学表达式,并对相应问题进行讨论。
【关键词】范德瓦尔斯气体;内能;熵;焓;自由能;绝热过程;节流过程Van der Waals gas thermodynamic propertiesChen Dong200806114( Qiannan Normal College for Nationalities Department of physics and electronic science, Guizhou Tuyun 558000)[ Abstract ] to discuss Van Der Waals gas internal energy, entropy, enthalpy and free energy, the corresponding mathematical expressions, and the relative problems are discussed.[ Key words ] Van Der Waals gas; energy; entropy; enthalpy; free energy; adiabatic process; throttling process理想气体是反映各种实际气体在压强趋于零时所共有的极限性质的气体,是一种理想模型。
在一般的压强和温度下,可以把实际气体近似地当作理想气体出来,但是在压强太大或温度太低(接近于其液化温度)时,实际气体与理想气体有显著的偏离。
为了更精确地描述实际气体的行为,人们提出很多实际气体的状态方程,其中最重要、最有代表性的是范德瓦尔斯方程。
1、范德瓦尔斯气体的状态方程范德瓦尔斯方程是在理想气体状态方程的基础上修改而得到的半经验方程。
理想气体是完全忽略除分子碰撞瞬间外一切分子间的相互作用力的气体,而实际气体就不能忽略分子间的作用力,原因是实际气体因压强大,分子数密度也大,分子间平均距离比理想气体小得多所致。


范德瓦尔斯气体内能
范德瓦尔斯气体内能是指气体分子在热力学平衡状态下所具有的内部能量。
这种内能是由于气体分子之间的相互作用而产生的,因此它与气体的压力、体积和温度等因素密切相关。
范德瓦尔斯气体是一种理想气体模型,它假设气体分子之间不存在相互作用力,因此其内能只与温度有关。
然而,在实际气体中,分子之间的相互作用力是不可避免的,因此范德瓦尔斯气体模型并不能完全描述实际气体的行为。
在实际气体中,分子之间的相互作用力会导致气体分子的内能发生变化。
当气体分子之间的相互作用力增强时,分子的内能也会增加,因为分子需要克服更大的相互作用力才能移动。
相反,当相互作用力减弱时,分子的内能也会减少。
范德瓦尔斯气体内能的变化还与气体的压力和体积有关。
当气体被压缩时,分子之间的相互作用力会增强,因此分子的内能也会增加。
相反,当气体被膨胀时,分子之间的相互作用力会减弱,因此分子的内能也会减少。
范德瓦尔斯气体内能是气体分子在热力学平衡状态下所具有的内部能量,它与气体的压力、体积和温度等因素密切相关。
在实际气体中,分子之间的相互作用力会导致气体分子的内能发生变化,因此范德瓦尔斯气体模型并不能完全描述实际气体的行为。
目 录摘 要 ................................................................................................... 1 Abstract ................................................................................................. 1 1 引 言 ................................................................................................. 1 2 范德瓦耳斯气体的热力学函数 (2)2.1范德瓦耳斯气体的熵(S ) (3)2.2 范德瓦耳斯气体的内能(U ) (4)2.3 范德瓦耳斯气体的焓(H ) (4)2.4 范德瓦耳斯气体的自由能(F ) ......................................................... 5 3范德瓦耳斯气体的摩尔容量 (5)3.1 范德瓦耳斯气体的P C 与V C 之差 (5)3.2 范德瓦耳斯气体的V C 与V 的关系 (7)3.3 范德瓦耳斯气体的P C 与P 的关系 ...................................................... 7 4结束语 ................................................................................................. 8 参考文献 (8)对范德瓦耳斯气体的热力学函数及热容量的研究摘 要:范德瓦耳斯方程是描述真实气体行为的基础。
本文从热力学函数的定义出发,结合范德瓦耳斯方程,推导出范德瓦耳斯气体的几个基本热力学函数,分析了其特性并研究了范德瓦耳斯气体的定容摩尔热容量和定压摩尔热容量的性质,指出了其同理想气体的区别。
正确理解热力学第三定律
苏许辉
【期刊名称】《物理通报》
【年(卷),期】2010(000)002
【摘要】分析了对热力学第三定律常见的错误理解,以能斯特定理为基础,通过推导得到了绝对零度不能达到的结论.
【总页数】2页(P21-22)
【作者】苏许辉
【作者单位】宁波中学,浙江,宁波,315100
【正文语种】中文
【相关文献】
1.热力学第三定律的发现者——能斯特 [J], 赵玉杰;杨谦;王洪见
2.范德瓦耳斯气体与热力学第三定律不相容 [J], 严子浚
3.关于热力学第三定律的思考 [J], 李效民
4.黑洞熵的演化规律与热力学第三定律 [J], 邓昭镜
5.热力学第三定律与经典理想气体模型的适用条件 [J], 常琳;孟泉水
因版权原因,仅展示原文概要,查看原文内容请购买。
范德瓦耳斯气体的热力学性质陈东2008061144(黔南民族师范学院物理与电子科学系,贵州都匀 558000)【摘要】讨论范德瓦尔斯气体的内能、熵、焓和自由能,给出相应的数学表达式,并对相应问题进行讨论。
【关键词】范德瓦尔斯气体;内能;熵;焓;自由能;绝热过程;节流过程Van der Waals gas thermodynamic propertiesChen Dong200806114( Qiannan Normal College for Nationalities Department of physics and electronic science, Guizhou Tuyun 558000)[ Abstract ] to discuss Van Der Waals gas internal energy, entropy, enthalpy and free energy, the corresponding mathematical expressions, and the relative problems are discussed.[ Key words ] Van Der Waals gas; energy; entropy; enthalpy; free energy; adiabatic process; throttling process理想气体是反映各种实际气体在压强趋于零时所共有的极限性质的气体,是一种理想模型。
在一般的压强和温度下,可以把实际气体近似地当作理想气体出来,但是在压强太大或温度太低(接近于其液化温度)时,实际气体与理想气体有显著的偏离。
为了更精确地描述实际气体的行为,人们提出很多实际气体的状态方程,其中最重要、最有代表性的是范德瓦尔斯方程。
1、范德瓦尔斯气体的状态方程范德瓦尔斯方程是在理想气体状态方程的基础上修改而得到的半经验方程。
理想气体是完全忽略除分子碰撞瞬间外一切分子间的相互作用力的气体,而实际气体就不能忽略分子间的作用力,原因是实际气体因压强大,分子数密度也大,分子间平均距离比理想气体小得多所致。
这一点从压强公式nkT P =可以清楚的看出来。
而组成宏观物体的分子间作用力包含引力和斥力两部分,不管分子间的引力还是斥力都是当分子接近到一定距离后才发生的,也就是说不管是分子间的引力还是斥力都是有力程的,而分子间的引力力程远大于斥力力程。
分子间短程而强大的斥力作用,使得分子间不能无限靠近,这相当于每个分子具有一定其他分子不能侵入的体积,因而在气体中,单个分子能够活动的空间不是气体所占据的体程V ,而是(vb V -),这里v 为气体的摩尔数,b 为1mol 气体分子具有的体积。
因此考虑到气体分子间的斥力存在,理想气体的状态方程应修改为vRT vb V P =-)(,或气体压强为)(vb V vRT P -=。
考虑到分子间的引力的存在,气体的压强比仅考虑分子间的斥力影响得出的vbV vRT - 还要小一个修正量P ∆,即P ∆称为气体的内压强,它是由于同器壁碰撞前分子受一个指向气体内的力引起的, a Vv P 2)(=∆ 将此式代入上式,得实际气体的状态方程为 22)(Vv a vb V vRT P --= 或vRT vb V Va v P =-+)(22)( 这就是范德瓦尔斯气体的状态方程。
对于 1摩尔气体的范德耳斯方程为RT b V Va P =-+))((2 (1) 式中V 为1mol 气体的体积,a,b 对一定气体来说都是常数,可以由实验测定。
通常是在一定温度下,测定与两个已知压强对应的两个υ值。
代人(1)式就可求出a 和b 。
2、 范德瓦尔斯气体的热力学函数2.1范德瓦尔斯气体的熵S已知1mol 范德瓦尔斯气体的状态方程是2Va b V RT P --= P vb V vRT P ∆--=)(由麦克斯韦关系式V T TP V S )(∂∂=∂∂)(得 bV R T P V S V T -=∂∂=∂∂)()( 对V 积分有 )(T b V R S ϕ+-=)ln(积分后出现的任意函数)(T ϕ与V 无关,它可以这样确定,当∞→V时范德瓦尔斯气体将连续地过渡为理想气体,而理想气体的熵式是 ⎰++=∞→0ln S V R TdT C S V V 代人上式得 ⎰+=0S TdT C T V )(ϕ 于是得范德瓦尔斯气体的熵函数为 ⎰+-+=0)ln(S b V R T dT C S V (2) 或 0)ln(ln S b V R T C S V +-+=比较范氏气体和理想气体的熵式,只有第二项不同,这是由于范氏气体考虑了分子间的作用力,所以1mol 的范氏气体单个分子能活动的空间不是气体所占据的体积V ,而是V-b 。
2.2范德瓦尔斯气体的内能U设),(V T U U = 则dV VU dT C dV V U dT T U dU T V T V )()()(∂∂+=∂∂+∂∂= (3) 应用能态方程求出代入上式积分得范德瓦尔斯气体的内能 0U Va dT C U V +-=⎰ (4) 对于理想气体的内能为⎰+=0U dT C U V可见范氏气体的内能还与体积有关,因为分子间的相互作用能量与分子的平均距离有关,因而内能与体积有关,而对于理想气体,气体足够稀薄,分子间的平均距离足够22)()()(Va V ab V RT b V R T P T P T V U V T =----=-∂∂=∂∂大,相互作用能量可以忽略,内能就与体积无关。
2.3范德瓦尔斯气体的焓H02U Va b V VRT dT C PV U H V +--+=+=⎰ (5) 2.4范德瓦尔斯气体的自由能F⎰⎰-+----=-=00)ln(TS U Va b V RT dT T C T dT C TS U F V V (6) 3、几个与范德瓦尔斯气体有重要关系的物理量3.1定容压强系数)()()(122b V a RTV RV b V P R T P P V ---=-=∂∂=β (7) 3.2等温压缩系数232223(2)()(211)(11)(1)b V a RT V b V V b V RT V a V V P V P V V K T T ---=---=∂∂-=∂∂-= (8)3.3定压膨胀系数2322222)(2)(.)(2)()()(1)(1b vV a RTV b V RV bV R b V a RT V b V V TP P V V T V V V T P ---=----=∂∂∂∂-=∂∂=α (9) 由于P 、V 、T 三个变量之间存在函数关系0),,(=T V P f 其偏导数之间存在下述关系 1)()()(-=∂∂∂∂∂∂P V T VT T P P V 因此以上三个系数之间存在如下关系P K βα= (10)它与物态方程的具体形式无关。
4、范德瓦尔斯气体在一些典型准静态过程中的性质4.1可逆绝热过程可逆绝热过程是等熵过程,由式(2)得 0)ln(0=-+=-⎰b V R T dT C S S V积分可得到范德瓦尔斯气体的准静态绝热方程为 常数=-V C Rb V T )((11) 把范德瓦尔斯气体的状态方程代入上式,上式又可写为 常数=-++V V C RC b V V a P ))((2 (12)4.2节流过程节流过程是一个等焓过程,尽管整个过程是不可逆的,我们可用热力学来联系它的初态和终态。
真实气体通过节流过程可以发生焦——汤姆逊效应。
焦——汤系数μ的定义为 ])([1)()()(V T V T C TH P H P T P P P T H -∂∂=∂∂∂∂-=∂∂=μ (13) 对于范德瓦尔斯气体,如我们取R C V 23=可由范德瓦尔斯气体定压摩尔热容与定容摩尔热容之差32)(21RTV b V a R C C V P --=-求得23223)(325)(21b V a TV R b V a RTV C P ----=又23332)(2)(]2)([b V a RTV b V RV Va b V RT b V R T V P ---=---=∂∂)( (14) 将以上各式代入(14)式可得])(325[])(2[122Vb V RTV a b V b V RT a R ----=μ (15) 由(15)式知,对于一个分子间有相互作用的范德瓦尔斯气体焦——汤系数可以变号。
(注意:摩尔体积V<b 时,范德瓦尔斯气体失去意义)由于低密度的气体总是满足b V a RTV ,,于是)2(52b RTa R -≈μ (16) 因此,在低温下0 μ在节流过程中气体冷却,但在高温0 μ,节流使气体发热,这正是焦耳——汤姆逊效应。
5、范德瓦尔斯气体在各热力学过程中的能量转化情况5.1等容过程外界对系统做的功:A=0;内能增量由式(3)可得:)(12T T C U V -=∆;吸收的热量)(12T T C U Q V -=∆=5.2等压过程内能增量:)11()(1212V V a T T C U V ---=∆.吸收的热量:)(12T T C Q P -=.外界对系统做的功: ).11())(()()1()(1212121212V V a T T C C T T C V V a T T C Q U A V P P V ----------=-∆=5.3等温过程内能增量:)]1()1[(-U 12V V a -=∆ ;外界对系统做的功: ⎰⎰-----=---=-=2121)11(ln )(12122V V V V V V a b V b V RT dV V a b V RT PdV A 吸收的热量:)ln(RT A -U Q 12b V b V --=∆=。
5.4绝热过程吸收的热量:Q=0;内能增量:⎰⎰⎰⎰---=+=+==∆21212121)11()()(U 121222V V V V V V V V V V V V V a T T C dV V a dT C dV Va dT C dU 外界对系统做的功:)11()(1212V V a T T C U A V ---=∆=。
5.5多方过程由多方过程方程:n n n b V V a P b V V a P b V V a )()()()()(P 222212112--+=--+=--+)(则外界对系统做的功: ⎰⎰---+-==2121])(1.))([(-A 21211V V V V n n dV Va b V b V V a P PdV )11(])[(11))((1211121211V V a b V b V n b V V a P n n n -------+=--)( )11()(11212V V a T T n R ----= 内能增量:)11()(1212V V a T T C U V ---=∆; 吸收的热量:)())(1(1212T T C T T n R C A U Q V -=---=-∆=参考文献:[1]李椿等编,热学高等教育出版社 1978年9月第1版[2]龚昌德,热力学与统计物理学人民教育出版社 1982年4月第1版[3][美]L.E.雷克、统计物理现代教程(上册)北京大学出版社 1983年4月第1版[4]刘国跃,范德瓦尔斯气体的热容量和准静态热力学过程的研究.绵阳经济技术高等专科学校学报,1998(3);74一75[5]张玉民编著,热学科学出版社第二版指导教师:奚可明讲师。