第二章 传递函数-梅逊公式
- 格式:ppt
- 大小:7.47 MB
- 文档页数:62

梅森公式求传递函数
梅森公式是一种常用的求解数字滤波器传递函数的方法。
数字滤波器是一种用于数字信号处理的滤波器,其传递函数描述了滤波器对输入信号的影响。
梅森公式可以用于求解各种类型的数字滤波器的传递函数,包括低通、高通、带通和带阻滤波器。
梅森公式的基本形式为:
H(z) = B(z) / A(z)
其中,B(z)和A(z)分别为数字滤波器的分子和分母多项式。
通过对分子和分母多项式进行系数的选择和取值,可以得到不同类型的数字滤波器传递函数。
例如,对于一个二阶低通数字滤波器,其分母多项式可以表示为: A(z) = 1 + a1*z^-1 + a2*z^-2
其中,a1和a2为系数。
通过选择合适的系数值,可以得到所需的滤波器响应特性。
类似地,分子多项式可以表示为:
B(z) = b0 + b1*z^-1 + b2*z^-2
也需要根据需要的响应特性进行系数的选择。
将分子和分母多项式代入梅森公式,即可求得数字滤波器的传递函数。
需要注意的是,在使用梅森公式求解数字滤波器传递函数时,需要考虑数字滤波器的采样率、截止频率等参数,以确保所得到的传递函数具有所需的滤波性能。
同时,由于数字滤波器的传递函数是离散的,因此在实际应用中需要进行数字信号的抽样和插值等处理,以确保信号处理的准确性和精度。








第二章控制系统的数学模型第10讲梅逊公式王燕舞梅逊(Mason)公式◆梅逊(Mason)公式是美国麻省理工学院S.J. Mason于20世纪50年代提出的。
借助于梅逊公式,不经任何结构变换,便可以得到系统的传递函数。
•∑L i :所有回路(n 条)的回路增益之和。
•∑L i L j :所有两两互不接触回路(n 2条)的回路增益乘积之和。
•∑L i L j L k :所有三三互不接触回路(n 3条)的回路增益乘积之和。
•P k :从输入节点到输出节点第k 条前向通路的增益。
•Δk :在Δ中,将与第k 条前向通路相接触的回路除去后所余下的部分的Δ ,称为余子式。
•m :从输入节点到输出节点所有前向通路的条数。
∆∆=∑=m k kk P s G 1)(+-+-=∆∑∑∑321111n kj i n j i n i L L L L L L ◆梅逊公式的表达式为:•G(s):待求的总传递函数。
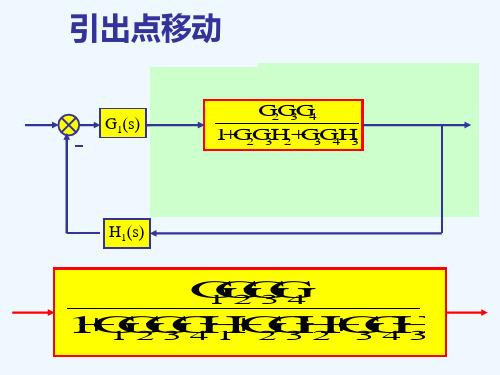
•Δ称为特征式,◆梅逊公式的证明:参见:1.Samuel J. Mason, “Feedback theory-Some properties ofsignal flow graphs,” Proc. IRE, vol. 41, no. 9, pp. 1144-1 156, Sept. 1953.2.Samuel J. Mason, “Feedback theory-Further properties ofsignal flow graphs,” Proc. IRE, vol. 44, no. 7, pp. 920-926, July 1956.3.W.K. Chen, “Applied Graph Theory, Graphs and ElectricalNetworks,” North-Holland, Amsterdam, 1976.4.陈景明, “S.J. Mason讯号流图增益公式的另一个证明,” 吉林大学自然科学学报, no. 4, pp. 137-146, 1979.G 3H 2G 2G 1G 4H 1CR G 5G 6H 4H 3-H 2G 2G 3-H 4G41G 6G 5-H 3CB E F G x 3H IR A 1G 1-H 11结构图信号流图求图示控制系统的传递函数。





§2-4 传递函数定义控制系统的传递函数为 在零初始条件下 ,输出信号的拉氏变换与输入 信号的拉氏变换之比。
表示为Y ( s ) bm s m + bm -1 s m -1 + ... + b1 s + b0 G( s) = = n , n ³ m (2-95) n -1 U (s) s + a n -1 s + ... + a1 s + a0系统的输出可表示为传递函数与控制输入的乘积Y ( s) = G ( s) × U ( s)(2-96)U(s)G(s)Y(s)回章首回节首12-4-3 控制系统的传递函数 1.复数阻抗U R (s) Z R ( s) = =R I R (s)(2-100)ZC ( s) =UC (s) 1 = I C ( s ) Cs(2-101)U L ( s) Z L ( s) = = Ls I L (s)回章首 回节首(2-102)22.典型环节 (1) 比例环节G(s) = Uo (s) =K Ui (s)(2) 积分环节G( s) = Uo ( s) 1 = Ui ( s) Ts(3) 微分环节U o (s) G (s) = = ts U i (s)3(4) 一阶惯性环节U o ( s) 1 G( s ) = = U i ( s) Ts + 1(5) 二阶振荡环节G( s) = U o ( s) 1 = 2 2 U i ( s ) T s + 2xTs + 1(6) 延迟环节G( s) = U o (s) = e -ts U i ( s)4画结构图时,所依据的原则是信号流通关系。
下面以实例来说明。
[例2-25] 已知两级RC网络如图2-33所示,作出该系 统的结构图。
解 设一个中间变量为电容C1 的电压Ux, 采 用复 数阻抗法顺序写出各 算子代数方程和方块图如下:回章首回节首5(1) U i ( s ) - U x ( s ) = U R1 ( s )(2) U R1 ( s ) × 1 = I ( s) R1(3) I ( s ) - I 2 ( s ) = I1 ( s )( 4) I 1 ( s ) × 1 = U x ( s ) C1 s(5) U x ( s ) - U o ( s ) = U R2 ( s )回章首回节首6(6) U R2 ( s ) × 1 = I 2 ( s ) R2 (7 ) I 2 ( s ) × 1 = U o ( s ) C2 s将各基本环节的方块按照信号流通方向连接起来 就可以得到如图2-33所示的系统方块图。


2-7 结构图等效变换及梅逊公式求传递函数时,需要对微分方程组(或变换方程组)进行消元,最后仅剩下输入、输出两个变量,因此中间变量的传递过程得不到反映。
若采用结构图,它就能形象地表明输入信号在系统或元件中的传递过程。
另外,下面将会看到,利用结构图,也便于求取传递函数。
所以,结构图在控制理论中应用十分广泛。
一、结构图在第2-6节中,我们曾采用消元法求得图2-24所示RC 网络的传递函数。
这里,我们采用结构图的方法求其传递函数。
RC 网络的微分方程组如下:⎪⎩⎪⎨⎧=+=⎰idt C u u Ri u c cr 1对上两式进行拉氏变换,得)()()(s U s RI s U c r +=或[])()()(1s I s U s U Rc r =- (2-54) )(1)(s I Css U r =(2-55)方程(2-54)可用图2-29)(a 表示,方程(2-55)可用图2-29)(b 表示。
将图2-29)(a )(b 按信号传递方向结合起来,网络的输入量置于图示的左端,输出量置于最右端,并将同一变量的信号连在一起,如图2-30)(a 所示,即得RC 网络结构图。
对图2-30)(a 进行所谓“等效变换”就可得出网络传递函数,因此网络结构就更为简单,如图2-30)(b 所示。
关于结构图等效变换的方法将另作介绍。
(1)建立控制系统各元、部件的微分方程。
(2)对各元、部件的微分方程进行拉氏变换,并做出各元、部件的结构图。
(3)按系统中各信号的传递顺序,依次将各元件结构图连接起来,便得到系统的结构图。
下面以图1-7所示随动系统为例。
把组成该系统各元部件的微分方程(2-18)进行拉氏变换,可得方程组(2-56e a ~),其中比较元件 )()()(s s s c r θθθε-=(2-56a ) 电位器 )()(1s K s U εεθ= (2-56b ) 放大器 )()(2s U k s U ε=(2-56c ) 电动机 )()()1(s U K s s T s m m =+εθ(2-56d ) 减速器)(1)(s is c θθ=(2-56e )各元、部件的结构图如图2-31所示。
