2.4框图化简及梅逊公式

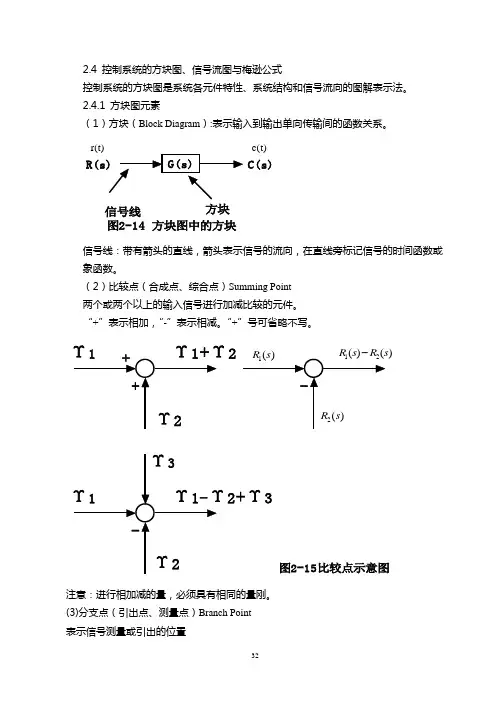
2.4 控制系统的方块图、信号流图与梅逊公式控制系统的方块图是系统各元件特性、系统结构和信号流向的图解表示法。

2.4.1 方块图元素（1）方块（Block Diagram ）:表示输入到输出单向传输间的函数关系。

C(s)图2-14 方块图中的方块信号线方块r(t)c(t)信号线：带有箭头的直线，箭头表示信号的流向，在直线旁标记信号的时间函数或象函数。

（2）比较点（合成点、综合点）Summing Point 两个或两个以上的输入信号进行加减比较的元件。

“+”表示相加，“-”表示相减。

“+”号可省略不写。

2)2+Υ3图2-15比较点示意图注意：进行相加减的量，必须具有相同的量刚。

(3)分支点（引出点、测量点）Branch Point 表示信号测量或引出的位置图2-16分支点示意图注意：同一位置引出的信号大小和性质完全一样。

2.4.2 几个基本概念及术语R(s)N(s)打开反馈图2-17 反馈控制系统方块图(1) 前向通路传递函数 假设N(s)=0打开反馈后，输出C(s)与R(s)之比。

在图中等价于C(s)与误差E(s)之比。

)()()()()(21s G s G s G s E s C == (2) 反馈回路传递函数 Feedforward Transfer Function 假设N(s)=0 主反馈信号B(s)与输出信号C(s)之比。

)()()(s H s C s B = (3) 开环传递函数 Open-loop Transfer Function 假设N(s)=0 主反馈信号B(s)与误差信号E(s)之比。

)()()()()()()(21s H s G s H s G s G s E s B == (4) 闭环传递函数 Closed-loop Transfer Function 假设N(s)=0 输出信号C(s)与输入信号R(s)之比。

)()(1)()()(1)()()()(21s G s H s G s G s H s G s G s R s C +=+= 推导：因为)()]()()([)()()(s G s H s C s R s G s E s C -== 右边移过来整理得)()(1)()()(s G s H s G s R s C += 即开环传递函数前向通路传递函数+=+=1)()(1)()()(s G s H s G s R s C **(5) 误差传递函数 假设N(s)=0 误差信号E(s)与输入信号R(s)之比。

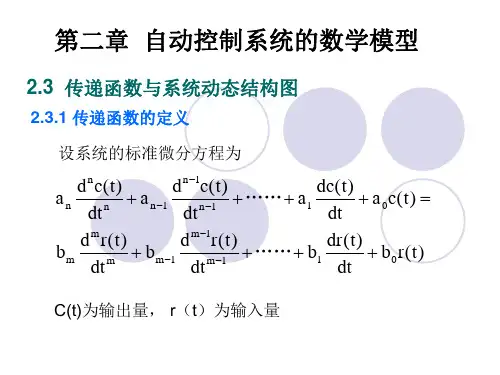
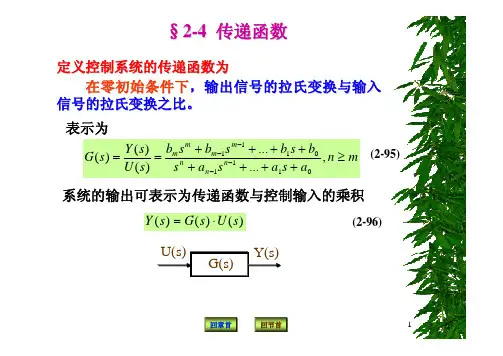
§2-4 传递函数定义控制系统的传递函数为 在零初始条件下 ，输出信号的拉氏变换与输入 信号的拉氏变换之比。

表示为Y ( s ) bm s m + bm -1 s m -1 + ... + b1 s + b0 G( s) = = n , n ³ m (2-95) n -1 U (s) s + a n -1 s + ... + a1 s + a0系统的输出可表示为传递函数与控制输入的乘积Y ( s) = G ( s) × U ( s)(2-96)U(s)G(s)Y(s)回章首回节首12-4-3 控制系统的传递函数 1．复数阻抗U R (s) Z R ( s) = =R I R (s)(2-100)ZC ( s) =UC (s) 1 = I C ( s ) Cs(2-101)U L ( s) Z L ( s) = = Ls I L (s)回章首 回节首(2-102)22．典型环节 (1) 比例环节G(s) = Uo (s) =K Ui (s)(2) 积分环节G( s) = Uo ( s) 1 = Ui ( s) Ts(3) 微分环节U o (s) G (s) = = ts U i (s)3(4) 一阶惯性环节U o ( s) 1 G( s ) = = U i ( s) Ts + 1(5) 二阶振荡环节G( s) = U o ( s) 1 = 2 2 U i ( s ) T s + 2xTs + 1(6) 延迟环节G( s) = U o (s) = e -ts U i ( s)4画结构图时，所依据的原则是信号流通关系。

下面以实例来说明。

[例2-25] 已知两级RC网络如图2-33所示，作出该系 统的结构图。

解 设一个中间变量为电容C1 的电压Ux， 采 用复 数阻抗法顺序写出各 算子代数方程和方块图如下:回章首回节首5(1) U i ( s ) - U x ( s ) = U R1 ( s )(2) U R1 ( s ) × 1 = I ( s) R1(3) I ( s ) - I 2 ( s ) = I1 ( s )( 4) I 1 ( s ) × 1 = U x ( s ) C1 s(5) U x ( s ) - U o ( s ) = U R2 ( s )回章首回节首6(6) U R2 ( s ) × 1 = I 2 ( s ) R2 (7 ) I 2 ( s ) × 1 = U o ( s ) C2 s将各基本环节的方块按照信号流通方向连接起来 就可以得到如图2-33所示的系统方块图。

果关
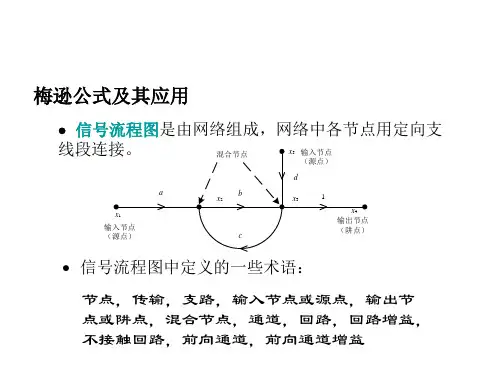
2.信号流图的性质
l信号流图适用于线性系统。

l支路表示一个信号对另一个信号的函数关系，信号只能沿支路上的箭头指向传递。

l在节点上可以把所有输入支路的信号叠加，并把相加后的信号送到所有的输出支路。

l具有输入和输出节点的混合节点，通过增加一个具有单位增益的支路把它作为输出节点来处理。

l对于一个给定的系统，信号流图不是唯一的，由于描述同一个系统的方程可以表示为不同的形式。

的方
一节点，
节点
小圆圈
条
＝
1
4条
：系统有单个路条,两两互不接路7
求：
2.4.6 闭环系统的传递函数。

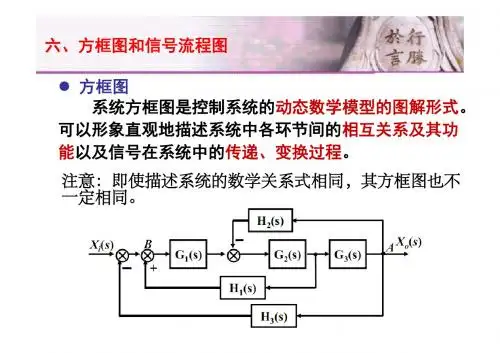
梅逊公式2.4 控制系统的方块图、信号流图与梅逊公式控制系统的方块图是系统各元件特性、系统结构和信号流向的图解表示法。

2.4.1 方块图元素（1）方块（Block Diagram ）:表示输入到输出单向传输间的函数关系。

C(s)图2-14 方块图中的方块信号线方块r(t)c(t)信号线：带有箭头的直线，箭头表示信号的流向，在直线旁标记信号的时间函数或象函数。

（2）比较点（合成点、综合点）Summing Point 两个或两个以上的输入信号进行加减比较的元件。

“+”表示相加，“-”表示相减。

“+”号可省略不写。

2)2+Υ3图2-15比较点示意图注意：进行相加减的量，必须具有相同的量刚。

(3)分支点（引出点、测量点）Branch Point 表示信号测量或引出的位置图2-16分支点示意图注意：同一位置引出的信号大小和性质完全一样。

2.4.2 几个基本概念及术语R(s)N(s)打开反馈图2-17 反馈控制系统方块图(1) 前向通路传递函数 假设N(s)=0打开反馈后，输出C(s)与R(s)之比。

在图中等价于C(s)与误差E(s)之比。

)()()()()(21s G s G s G s E s C == (2) 反馈回路传递函数 Feedforward Transfer Function 假设N(s)=0 主反馈信号B(s)与输出信号C(s)之比。

)()()(s H s C s B = (3) 开环传递函数 Open-loop Transfer Function 假设N(s)=0 主反馈信号B(s)与误差信号E(s)之比。

)()()()()()()(21s H s G s H s G s G s E s B == (4) 闭环传递函数 Closed-loop Transfer Function 假设N(s)=0 输出信号C(s)与输入信号R(s)之比。

)()(1)()()(1)()()()(21s G s H s G s G s H s G s G s R s C +=+= 推导：因为)()]()()([)()()(s G s H s C s R s G s E s C -== 右边移过来整理得)()(1)()()(s G s H s G s R s C += 即开环传递函数前向通路传递函数+=+=1)()(1)()()(s G s H s G s R s C **(5) 误差传递函数 假设N(s)=0 误差信号E(s)与输入信号R(s)之比。