§2.5闭环传递函数§2.6 梅逊公式
- 格式:ppt
- 大小:4.65 MB
- 文档页数:30
2.4 控制系统的方块图、信号流图与梅逊公式控制系统的方块图是系统各元件特性、系统结构和信号流向的图解表示法。
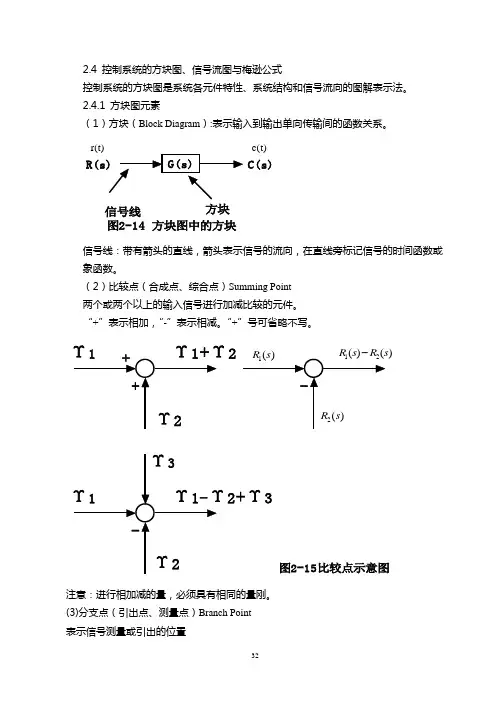
2.4.1 方块图元素(1)方块(Block Diagram ):表示输入到输出单向传输间的函数关系。
C(s)图2-14 方块图中的方块信号线方块r(t)c(t)信号线:带有箭头的直线,箭头表示信号的流向,在直线旁标记信号的时间函数或象函数。
(2)比较点(合成点、综合点)Summing Point 两个或两个以上的输入信号进行加减比较的元件。
“+”表示相加,“-”表示相减。
“+”号可省略不写。
2)2+Υ3图2-15比较点示意图注意:进行相加减的量,必须具有相同的量刚。
(3)分支点(引出点、测量点)Branch Point 表示信号测量或引出的位置图2-16分支点示意图注意:同一位置引出的信号大小和性质完全一样。
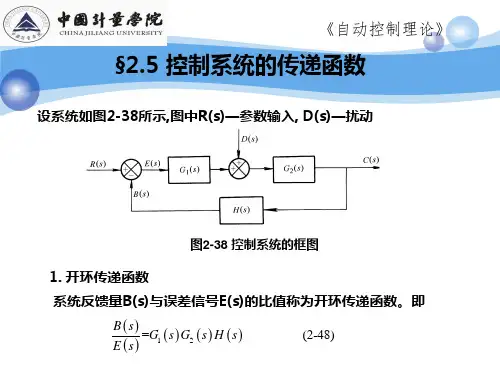
2.4.2 几个基本概念及术语R(s)N(s)打开反馈图2-17 反馈控制系统方块图(1) 前向通路传递函数 假设N(s)=0打开反馈后,输出C(s)与R(s)之比。
在图中等价于C(s)与误差E(s)之比。
)()()()()(21s G s G s G s E s C == (2) 反馈回路传递函数 Feedforward Transfer Function 假设N(s)=0 主反馈信号B(s)与输出信号C(s)之比。
)()()(s H s C s B = (3) 开环传递函数 Open-loop Transfer Function 假设N(s)=0 主反馈信号B(s)与误差信号E(s)之比。
)()()()()()()(21s H s G s H s G s G s E s B == (4) 闭环传递函数 Closed-loop Transfer Function 假设N(s)=0 输出信号C(s)与输入信号R(s)之比。
)()(1)()()(1)()()()(21s G s H s G s G s H s G s G s R s C +=+= 推导:因为)()]()()([)()()(s G s H s C s R s G s E s C -== 右边移过来整理得)()(1)()()(s G s H s G s R s C += 即开环传递函数前向通路传递函数+=+=1)()(1)()()(s G s H s G s R s C **(5) 误差传递函数 假设N(s)=0 误差信号E(s)与输入信号R(s)之比。

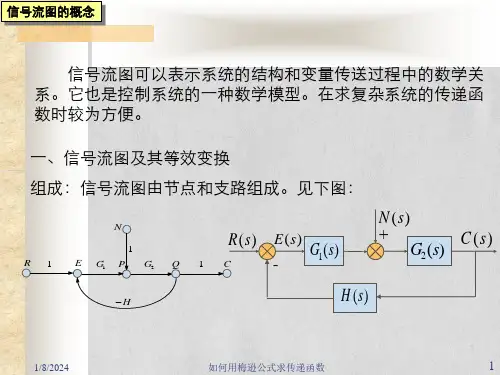
梅森公式求传递函数梅森公式求传递函数在探讨开环传递函数和闭环传递函数之前,我们需要先了解一些基础知识。
传递函数通常是指线性系统的输出与输入之间的关系,其中输入通常是一个函数,输出也是一个函数。
当我们了解传递函数的性质时,我们可以更好地设计控制系统,调整输入,使输出达到我们所需的目标。
在这里,我们将重点介绍梅森公式是如何求解传递函数的,梅森公式是一种常见的、快速且可靠的方法,用于解决反馈控制系统的稳定性问题。
梅森公式是一种特殊的公式,它同时适用于电气和机械系统,尤其适用于系统的加减法运算芯片,用于测量和放大信号。
首先,我们需要了解梅森公式的组成部分——单位环,单位环是指输入信号沿着反馈路径回到输入的路径。
这通常是因为系统的输出通过反馈路径的增强或减弱,来调节系统的调制。
如果我们能够计算出反馈路径的增强和输入信号的比例,我们就可以确定系统的传递函数了。
那么,如何确定反馈路径的增强和输入信号的比例呢?这就需要用到梅森公式了。
梅森公式表明,任何一个带有反馈路径的系统都可以由输入的单位环来描述。
在这种情况下,反馈系数是最小的。
因此,我们可以通过计算单位环的增益和相位移,来确定系统的传递函数。
梅森公式的常见形式为:$H(s) = \frac{N(s)}{D(s)} =\frac{1}{\Delta}\sum_{i=1}^{n}(-1)^{i+1}\Delta_i(s)\frac{D_i(s)}{N_i(s)}$其中,$\Delta$为通分多项式,$D(s)$为系统的分母多项式,$N(s)$为系统的分子多项式,$D_i(s)$和$N_i(s)$为单位环考虑时的分母多项式和分子多项式,$\Delta_i(s)$为通分多项式的第$i$个因式。
这个梅森公式看起来很复杂,但它告诉我们的是,我们可以把系统的分子多项式和分母多项式分解成多个分式(即$\frac{D_i(s)}{N_i(s)}$),然后通过单位环考虑时,根据各个分式的反馈系数(即$(-1)^{i+1}$)和分式的分母和分子多项式得到系统的传递函数。






2-7 结构图等效变换及梅逊公式求传递函数时,需要对微分方程组(或变换方程组)进行消元,最后仅剩下输入、输出两个变量,因此中间变量的传递过程得不到反映。
若采用结构图,它就能形象地表明输入信号在系统或元件中的传递过程。
另外,下面将会看到,利用结构图,也便于求取传递函数。
所以,结构图在控制理论中应用十分广泛。
一、结构图在第2-6节中,我们曾采用消元法求得图2-24所示RC 网络的传递函数。
这里,我们采用结构图的方法求其传递函数。
RC 网络的微分方程组如下:⎪⎩⎪⎨⎧=+=⎰idt C u u Ri u c cr 1对上两式进行拉氏变换,得)()()(s U s RI s U c r +=或[])()()(1s I s U s U Rc r =- (2-54) )(1)(s I Css U r =(2-55)方程(2-54)可用图2-29)(a 表示,方程(2-55)可用图2-29)(b 表示。
将图2-29)(a )(b 按信号传递方向结合起来,网络的输入量置于图示的左端,输出量置于最右端,并将同一变量的信号连在一起,如图2-30)(a 所示,即得RC 网络结构图。
对图2-30)(a 进行所谓“等效变换”就可得出网络传递函数,因此网络结构就更为简单,如图2-30)(b 所示。
关于结构图等效变换的方法将另作介绍。
(1)建立控制系统各元、部件的微分方程。
(2)对各元、部件的微分方程进行拉氏变换,并做出各元、部件的结构图。
(3)按系统中各信号的传递顺序,依次将各元件结构图连接起来,便得到系统的结构图。
下面以图1-7所示随动系统为例。
把组成该系统各元部件的微分方程(2-18)进行拉氏变换,可得方程组(2-56e a ~),其中比较元件 )()()(s s s c r θθθε-=(2-56a ) 电位器 )()(1s K s U εεθ= (2-56b ) 放大器 )()(2s U k s U ε=(2-56c ) 电动机 )()()1(s U K s s T s m m =+εθ(2-56d ) 减速器)(1)(s is c θθ=(2-56e )各元、部件的结构图如图2-31所示。