梅逊增益公式及应用

梅森增益公式适用范围标题：梅森增益公式适用范围的阐述引言：梅森增益公式是电子电路设计中常用的一种分析工具，用于计算电路增益和频率响应。

然而，在实际应用中，梅森增益公式的适用范围有一定限制。

本文将就梅森增益公式的适用范围展开阐述，以帮助读者更好地理解和使用这一公式。

一、梅森增益公式简介梅森增益公式是一种基于网络理论的公式，用于计算复杂电路的总增益。

它是由美国电子工程师梅森提出的，一般用于线性、定常、时不变的电路分析。

二、适用范围的限制1. 线性电路要求梅森增益公式适用于线性电路，即电路的元件和信号是线性的。

对于非线性电路，例如包含二极管、晶体管等非线性元件的电路，梅森增益公式就不再适用。

2. 定常电路要求第1页/共6页梅森增益公式适用于定常电路，即电路的参数是固定的，不随时间变化。

对于具有非定常特性的电路，如含有开关、变阻器等可变元件的电路，梅森增益公式无法提供准确的结果。

3. 时不变电路要求梅森增益公式适用于时不变电路，即电路的参数与时间无关。

在实践中，例如考虑温度变化、电源变化等因素会导致电路参数发生改变，因此这些情况下梅森增益公式不能得到准确的结果。

三、梅森增益公式的优势尽管梅森增益公式存在一定的适用范围限制，但它仍然是电子电路设计中常用的工具。

以下是梅森增益公式的一些优势：1. 简单易用相比其他复杂的电路分析方法，梅森增益公式简单易懂，计算过程相对简单直观。

这使得它成为工程师们在电路设计、故障排除等方面的重要工具。

2. 可模块化分析梅森增益公式支持对电路进行模块化分析。

通过将复杂的电路划分为多个子电路，可以使用梅森增益公式计算每个子电路的增益，进而得到整个电路的总增益。

这种分析方法便于对电路进行优化和调试。

第2页/共6页3. 提供定量分析结果梅森增益公式给出的是数值化的增益结果，可以帮助工程师量化地评估和比较不同电路的性能。

这对于电路设计者来说非常重要，可以在设计初期对各个子电路进行评估和优化。

具有任意条前向通路及任意个单独回路和不接触回路的复杂信号流图，求取从任意源节点到任意阱节点之间传递函数的梅森增益公式记为
式中
——从源节点到阱节点的传递函数（或总增益）；
——从源节点到阱节点的前向通路总数；
——从源节点到阱节点的第
条前向通路总增益；
——流图特征式
式中
——所有单路回路增益之和；
——所有互不接触的单独回路中，每次取其中两个回路的回路增益的乘积之和；
——所有互不接触的单独回路中，每次取其中三个回路的回路增益的乘积之和；
——流图余因子式，它等于流图特征式中除去与第
条前向通路相接触的回路增益项（包括回路增益的乘积项）以后的余项式。

[1]。

是包含于，你理解的有点偏差，举个例子如果有三个互不接触的回路，取两个不接触的回路应有三项，取三个互不接触回路就一项。

具体的应该是这样：
梅森公式G(s)=Σ(Ρκ*△κ)╱△G(s)= ——系统总传递函数；n——是前向通道数；Ρκ——第k条前向通路的传递函数，由输入端单向传递至输出端的信号通道称为前向通道；△——流图的特征式△=1-ΣLi+ΣLjLk-ΣLiLjLk+······
L A
bc为每两个不接触回路增益乘积之和
a为所有回路增益之和；L a L b
Li——所有单独回路的增益之和；
LjLk——所有互不接触的单独回路中，取其中两个不接触的回路增益乘积之和；LiLjLk——所有互不接触的单独回路中，取三个互不接触回路增益之和；
△κ——第k条前向通路特征式的余因子，即对于流图的特征式△，将与第k 条前向通路相接触的回路
增益代以零值，余下的即为△κ。

对于复杂的结构，理论上有很多项，但实际上△就取到前两三项。

1、信号流图的起源信号流图的起源是梅逊（mason)利用图解法表示一个或一组线性方程组并图解求解的方法。

（1956年） 如：欧姆定律 U=IR.U如：五个变量的一组代数方程式： 45253442331211cx gx dx x bx x fx ax x ex x x x x ++==+=+==2、信号流图的表示节点表示系统的变量，从左到右顺序设置。

每个节点标志的变量是所有流向该节点的信号之代数和，而从同一节点流向各支路的信号均用该节点的变量表示。

支路相当于乘法器。

信号在支路上只能沿箭头单向传递。

节点分为输入节点，如上图x1，只有输出而无输入； 输出节点，如上图x5，只有输入而无输出；混合节点，如上图x2,x3,x4，既有输入又有输出。

3、几个名词的定义前向通路：信号从输入节点到输出节点传递时，每个节点只通过一次的通路。

前向通路增益为各个支路的增益乘积。

如：x1->x2->x3->x4->x5. 前向通路增益为p1=abc；x1->x2 ->x5. 前向通路增益为p2=d。

回路：起点和终点在同一节点，而且信号通过每一节点不多于一次的闭合通路称为回路。

回路增益：回路中所有支路增益乘积。

如：x2->x3 ->x2. 回路1增益L1=ae；X3->x4 ->x3. 回路2增益L2=bf；X5->x5. 回路3增益L3=g。

不接触回路：回路之间没有公共节点时，称不接触回路。

如：回路1和回路3；回路2和回路3。

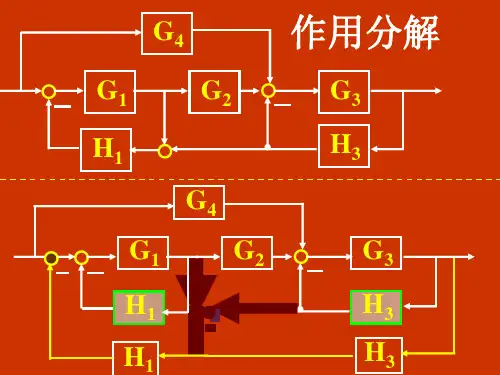
4、信号流图的绘制由动态结构图绘制4、梅逊增益公式来源：按克莱姆法则求解线性联立方程组时，将解的分子多项式及分母多项式与信号流图巧妙联系的结果。

图中有3个独立回路，没有互不接触的回路。

前向通路只有一条，与所有回路都接触。

∆∆=∑=nk kk P s G 1)(之后的余子式。

路所在项去掉条前向通道相接触的回中与第：将；个前向通道的传递函数第之和。

梅森公式经典例题摘要：一、梅森公式简介1.梅森公式的定义2.梅森公式在数学中的重要性二、经典例题解析1.例题一：利用梅森公式求解2.例题二：利用梅森公式求解3.例题三：利用梅森公式求解三、例题解答与总结1.例题一解答2.例题二解答3.例题三解答4.总结：梅森公式在解题中的应用与技巧正文：一、梅森公式简介梅森公式，又称伯努利公式，是数学领域中一个非常重要的公式。

它是由瑞士数学家雅各布·伯努利（Jacob Bernoulli）提出的，用于描述调和级数的性质。

梅森公式在数学中具有很高的地位，被广泛应用于组合数学、概率论、数论等多个领域。

二、经典例题解析接下来，我们将通过三个经典例题来解析梅森公式在实际问题中的应用。

例题一：利用梅森公式求解题目：已知等差数列的前n 项和为S_n，求S_n^2 与n^3 之间的关系。

解答：根据梅森公式，我们可以得到S_n = n*(2a + (n-1)*d)/2，其中a 为数列的首项，d 为公差。

将S_n 代入S_n^2 中，我们可以得到S_n^2 = n^2*(4a^2 + 4a*d + d^2 + 2a*(n-1)*d)/4。

通过化简，我们可以发现S_n^2 与n^3 之间的关系为S_n^2 = n^2*(2a^2 + 2a*d + d^2)/4 +n^3*(a*d - a^2)/4。

例题二：利用梅森公式求解题目：求解组合数C(n, k) 的梅森公式表示。

解答：根据梅森公式，我们可以得到C(n, k) = n! / (k! * (n-k)!)。

将C(n, k) 的定义代入梅森公式中，我们可以得到C(n, k) = (n*(n-1)*...*(n-k+1)) / (k*(k-1)*...*1)。

进一步化简，我们可以得到C(n, k) = n*(n-1)*...*(n-k+1) / k!。

例题三：利用梅森公式求解题目：已知正整数n，求解1^2 + 2^2 + ...+ n^2 的值。

梅森增益公式适用范围
【最新版】
目录
一、梅森增益公式的背景和来源
二、梅森增益公式的定义和含义
三、梅森增益公式的适用范围和应用实例
四、梅森增益公式的优点和局限性
正文
一、梅森增益公式的背景和来源
梅森增益公式，是由塞缪尔·杰斐逊·梅森推导出的一种用于计算信号流图（即拓扑图）中节点增益的公式。

该公式的来源可以追溯到按克莱姆（Gramer）规则求解线性联立方程式组时，将解的分子多项式及分母多项式与信号流图巧妙联系的结果。

二、梅森增益公式的定义和含义
梅森增益公式是一种用于计算从源节点到阱节点的传递函数（或总增益）的方法。

公式如下：
P = 1 + Σ(pk * Gk)
其中，P 为从源节点到阱节点的传递函数（或总增益），n 为从源节点到阱节点的前向通路总数，pk 为从源节点到阱节点的第 j 条前向通路总增益，Gk 为第 j 条前向通路的增益。

三、梅森增益公式的适用范围和应用实例
梅森增益公式主要适用于控制系统和信号处理领域，特别是在处理多变量、多回路包括内循环回路的信号流图时，具有很好的实用性。

例如，在电子电路、通信系统、自动控制等领域，梅森增益公式可以帮助工程师
快速准确地计算出系统的总增益，从而为系统的设计和优化提供有力支持。

四、梅森增益公式的优点和局限性
梅森增益公式的优点在于，它可以通过检查信号流图确定，并且可以很容易地处理多变量、多回路包括内循环回路的信号流图。

此外，该方法还可以求解多元方程组，从而得到系统的传递函数。

然而，梅森增益公式也存在一定的局限性。

首先，它仅适用于线性系统，对于非线性系统则无法适用。