平行线角平分线构造等腰三角形专题

龙文教育个性化辅导教案讲义任教科目：授课题目：年级：任课教师：授课对象：武汉龙文个性化教育常青二校区教研组组长签字：教学主任签名：日期：武汉龙文教育学科辅导讲义教学流程及授课详案一由课本例题引入1 近几年中考题往往由平行线，角平分线来推证同一三角形两个角相等，从而推证两边相等。

或者由其中两个条件推证另一个条件例 (1)AD是 ABC的外角平分线，（2）AD // BC （3）求证： ABC是等腰三角形分析讨论想一想能不能由（1）（3）证明（2）或者（2）（3）证明（1）？变式（2012京门）已知：如图7－9，在ΔABC中，CE是角平分线，EG∥BC，交AC边于F，交∠ACB的外角（∠ACD）的平分线于G，探究线段EF 与FG的数量关系并证明你的结论．EFCBAD2试一试1、 （2011）如图,AC 和BD 相交于O ，且AB ∥DC ，OA=OB, 求证：OC=OD.2．（2012）如图，△ABC 中，AM ，CM 分别是角平分线，过M 作DE ∥AC 求证：AD+CE=DE 3．（2012）如图，∠AOB=30°，OC 平分∠AOB ，CD ⊥OA 于D ，CE ∥AO 交OB 于E CE=20cm ，求CD 的长。

4．（2012）如图，△ABC 中，∠A =36°，AB =AC ，BD 平分∠ABC ，DE ∥BC ，则图中等腰三角形的个数（ ）（A ）1个 （B ）3个 （C ）4个 （D ）5个5（2012北京）、如右图：∠DAE=∠ADE=15°，DE∥AB，DF⊥AB，若AE=8，则DF 等于（ ）Ａ．5 Ｂ．4 C ． 3D ．2ODCBAAEB CD 第16题例2（2012浙江）．（8分）如图， AD ∥BC ，BD 平分∠ABC ，∠A=120°，∠C=60°，AB=CD=4cm ，求四边形ABCD 的周长．[来源:Z*xx*]三 课堂小结1 当题目中有角平分线时，可通过构造等腰三角形或全等三角形来寻找解题思路，或利用角平分线性质去证线段相等：要证明两条线段的和与一条线段相等时常用的两种方法： （1）、可在长线段上截取与两条线段中一条相等的一段，然后证明剩余的线段与另一条线段相等。

平行四边形——常用模型（二）平行线、角平分线和等腰三角形
“三兄弟”——平行线、角平分线和等腰三角形经常会在平行四边形这一章进行运用，是必须要熟练掌握的模型，作为组合类辅助线，看见其二，还要想到构造另外一个，考察最多的是平行线+角平分线，延长法构造等腰三角形.
下面让我们一起来研究下：
一、平行线+角平分线
如图，AD∥BC，AE平分∠BAD，则AB=BE.
∵AD∥BC
∴∠EAD=∠BEA
∵AE平分∠BAD
∴∠BAE=∠EAD
∴∠BAE=∠BEA
∴AB=BE
二、角平分线+等腰三角形
如图，AE平分∠BAD，AB=BE，则AD∥BC.
∵AE平分∠BAD
∴∠BAE=∠EAD
∵AB=BE
∴∠BEA=∠BAE
∴∠BEA=∠EAD
∴AD∥BC
三、平行线+等腰三角形
如图，AD∥BC，AB=BE，则AE平分∠BAD.
∵AD∥BC
∴∠BEA=∠EAD
∵AB=BE
∴∠BAE=∠BEA
∴∠BAE=∠EAD
∴AE平分∠BAD
四、平行线+角平分线（辅助线）
延长法（延长角平分线）构造等腰三角形
如图，AB∥CD，CE平分∠ACD，则
延长CE交AB于点F，
易得：△ACF是等腰三角形.
结语：
平行线，角平分线，等腰三角形就像三兄弟，他们形影不离，题目中出现其中二个，要想到另外一个，如果没有，可以通过添加辅助线得到另外一个。

只有熟练掌握了，我们才能提高做题效率。

练习：。

模型“平行线”、“角平分线”、“等腰三角形”三者知二推一【几何模型】“角平分线”、“平行线”、“等腰三角形”三者知其二必推出其一。

初中数学学习难在几何题没有思路当然了，有了思路就感觉简单了，那么为什么没有思路？关键是没有掌握几何证明题的本质，他是一个推理过程，就是具备什么条件，一定会具有一个结论。

往往对推理过程不熟练，思考不到条件下结论存在性，挖空心思也写不出步骤。

这就需要训练做题，思考总结出具备什么条件会有什么结论，做题时直奔主题，不用再思考了，日积月累，书到渠成，再解决几何问题就不难了。

在△ABC中，∠BAC=α[定值]，BC=a[定值]，可得“定弦定角”模型，找隐圆；【例题】：挖掘定角与定线背景内涵，思考最值问题第25题初审可知第三问考查定角定中线模型（附尺规作图）及解法；联想到定角定高模型（参考题:2020年沈河一模第25题）；最后小编原创题考查定角定角平分线。

【思维教练3】—“知识储备”前文已更新：倍长中线，构造“定弦定角”模型，找到隐圆求解。

亦可构造等边三角形转化线段，得：“共顶点的两个等边三角形”；其中，方法二：根据“垂线段最短”得：CK≤CG，则CK的最大值为2√(3)，CM+CN=EF+EN=FN；【你看出思路了吗】小编原创试题“考查定角定角平分线”，1．如图，点A、B、C、D在⊙O上，AD平分∠BAC．若∠B O C＝120°，则∠C AD的度数为．2．如图，AD是△ABC的外接圆⊙O的直径．若∠BCA＝50°，则∠AD B的度数为．3．已知圆锥的底面半径为1cm，高为cm，则它的侧面展开图的面积为cm²．4．如图，AB是半圆O的直径．弦CD∥AB，CD＝8，AB＝10，则CD与AB之间的距离为．5．如图，在⊙O中，点A在弧BC上．若∠B O C＝100°，则∠BA C的度数为．▱ABCD的6．如图，若用半径为8，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面圆半径是．7．如图，已知锐角△ABC内外接于半径为2的⊙O．若OD⊥BC于点D，∠BAC＝60°，则OD＝．8．如图，AD是△ABC的外接圆⊙O的直径．若∠BAD＝40°，则∠AC B的度数为．9．已知圆锥的母线长为3，底面圆半径为1，则该圆锥的侧面展开图的面积为．10．已知圆锥的底面圆半径为3，侧面面积为12，则该圆锥的母线长为．11．在⊙O中，若弦BC垂直平分半径O A，则弦BC所对的圆周角等于．12．如图，已知AB是⊙O的直径．P A切⊙O于点A，线段P O交⊙O于点C，连接BC．若∠P＝36°，则∠B＝．13．用一个圆心角为90°，半径为20 cm的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面圆半径是．14．已知圆锥的底面圆半径为2.5，母线长为9，则该圆锥的侧面展开图的圆心角度数为．15．如图，在边长为2的正方形ABCD中，对角线AC的中点为点O，分别以点A、C为圆心，以AO的长为半径画弧，分别与正方形ABCD的边相交，则图中阴影部分的面积为．（结果保留）16．如图，在△A BC中，∠C＝90°，AC＝4，BC＝3．若以A C所在直线为轴，把△A BC旋转一周，得到一个圆锥，则这个圆锥的侧面面积是．17．如图，在△A BC中，若∠A CB＝45°，A B＝6．则△A BC的面面积的最大值是．18．如图，在扇形△AO B中，OA＝O B＝2，∠AO B＝90°，点C为弧A B上一点．∠AO C＝30°，连接BC，过点C作OA的垂线交OA于点D，则图中阴影部分的面积为．19．如图，点A、B、C、D为一个正多边形的顶点，点O为正多边形的中心，若∠AD B＝18°，则这个正多边形的边数为．20．如图，在半径为6的⊙O中．若∠AO B＝60°，则图中阴影部分的面积为．21．用一个圆心角为120°，半径为4的扇形制作一个圆锥的侧面（接缝忽略不计），则此圆锥的底面圆半径是．3一．圆典型基本模型图模型1图形：⑴如图，A B是⊙O的直径，点C、E是⊙O上的两点．基本结论有：①A C平分∠B AE是；②A D⊥CD；③CD是⊙O的切线；三个论断，知二推一．⑵⑶⑷⑸⑹④⑤⑥如图，A B是⊙O的直径，点C、E是⊙O上的两点．20．如图，在半径为6的⊙O中．若∠AO B＝60°，则图中阴影部分的面积为．接圆的直径．若∠BCA＝50°，则∠AD B的度数为．∠A BACDB O＝90°，2．如图，在每个小正方形边长为1的网格中，△ABC的顶点A、B、C均在格点上，AB与网格交于点D．AD的长为；OP．AB2A2B，A′B′OP．AB2A2B，A′B′OP．AB2A2B，A′B′（2）点P是边AC上一点，当△APD∽△ABC时，仅用无刻度的直尺确定点P的位置，简单说明作图方法（不要求证明）．≌≌≌1．如图，在每个小正方形的边长为1的网格中，点O、点A在格点上，⊙O的半径为3，点B、点C在⊙O上．½∥⅓⅔¼°²³ⁿ∵∴⑥⑦½∥⅓⅔¼°²³ⁿ∵∴⑥⑦½∥⅓⅔¼°²³ⁿ∵∴⑥⑦´＇´＇´＇（1）若∠⊥CAO＝90°，ADAC的长为；①②③B．②④①②③B．②④（2）若∠BAO＝60°，仅用无刻度的直尺确定点B的位置，简单说明作图方法．⊙O上．2．如图，在每个小正方形边长为1的网格中，△ABC的顶点A、B、C均在格点上，AB与格交于点D．（2）点P是边AC上一点，当△APD∽△ABC时，仅用无刻度的直尺确定点P的位置，简单说明作图方法（不要求证明）．过点O作OQ∥AP交BM于点Q，过点P作PE⊥AB于点C，交QO的延长线于点E，连接PQ，OP．AB2A2B，BD＝n•BF，沿A→B→C→D→A方向运动到点A 处停止．过点O作OQ∥AP交BM于点Q，过点P作PE⊥AB∏于点C，交QO的延长线于点E，连接PQ，cm BD＝n•BF，沿A→B→C→①②⑤①②⑤①②⑤精选试题解析（1）。

专题12 构造等腰三角形的常用方法（原卷版）类型一作一腰的平行线构造等腰三角形1．如图，△ABC中，AB＝AC，D在AB上，F在AC的延长线上，且BD＝CF，连接DE交BC于E．求证：DE＝EF．2．（2020秋•义马市期中）如图，在等腰△ABC中，AB＝AC，∠BAC＝45°，BD⊥AC，点P为边AB上一点（不与点A、点B重合），PM⊥BC，垂足为M，交BD于点N．请猜想PN与BM之间的数量关系，并证明．3．（2020秋•九龙坡区期中）如图，在△ABC中，AD平分∠BAC交BC边于点D，点E是BC边的中点，线段EF∥AD交线段AB于点G，交线段CA的延长线于点F．（1）若CF＝6，AG＝2，求AC的长；（2）求证：BG＝CF．类型二利用角平分线+垂线构造等腰三角形4．（2021春•万柏林区校级月考）如图，△ABC的面积为6cm2，AP垂直∠ABC的平分线BP于点P，则△PBC的面积是cm2．5．（2021秋•上杭县期中）已知：如图，DE平分∠AEB，∠B＝∠EAC，ED⊥AD于D．求证：AD平分∠BAC．类型三利用截长补短法构造等腰三角形6．（2021秋•拱墅区期中）如图，AD是△ABC的高，且AB+BD＝DC，∠BAD＝40°，则∠C的度数为．7．（2020秋•绵阳期末）如图，在△ABC中，∠BAC＝120°，AD⊥BC于D，且AB+BD＝DC，求∠C的度数．8．（2023春•雨城区校级期中）已知△ABC中，AB＝AC，BE平分∠ABC交边AC于E．（1）如图（1），当∠BAC＝108°时，证明：BC＝AB+CE；（2）如图（2），当∠BAC＝100°时，（1）中的结论还成立吗？若不成立，是否有其他两条线段之和等于BC，若有请写出结论并完成证明．类型四利用倍角关系构造等腰三角形9．（2020秋•南岗区月考）如图，AD平分∠BAC，∠ABC＝3∠C，BE⊥AD垂足为E，AB＝8，BE＝2.5，则AC＝．10．已知E为△ABC内部一点，AE延长线交边BC于点D，连接BE、CE，∠BED＝∠BAC＝2∠DEC，如图，若AC＝AB，求证：BE＝2AE．类型五作底边的平行线构造等腰三角形12．如图，等边△ABC中，D在边AC延长线上一点，延长BC至E，使CE＝AD，DG⊥BC于G，求证：BG＝EG．13．（2012秋•五河县期末）如图，过等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，且P A＝CQ，连PQ交AC边于D．（1）求证：PD＝DQ；（2）若△ABC的边长为1，求DE的长．类型六构造等边三角形15．（华容区校级期中）如图，已知在△ABC中，AB＝AC，∠A＝20°，D，E分别为AC，AB上的点，∠DBC＝60°，∠ECB＝50°，则∠BDE＝．16．如图，在△ABC中，∠ABC＝∠ACB＝40°，P为三角形内的一点，且∠PCA＝20°，∠P AB＝20°，求∠PBC的度数．。

角平分线与平行线构造等腰三角形问题基本图形1已知： AB∥CD, （1）CE平分∠ACD交AB于E.问⊿ACE是什么特殊三角形？（2）反过来，若AC＝AE,问CE是∠ACD的平分线吗?基本图形2已知：△ABC,AB＝AC,（1）AE是外角∠BAD的平分线.问AE与BC平行吗？（2）若AE∥BC，问∠DAE＝∠BAE吗？（3）若AE是外角∠BAD的平分线，且AE∥BC，AB＝AC吗？问题举例1.已知：如图，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F，求证：四边形AEDF是菱形。

2．（2016•泰安）如图，在□ABCD中，AB=6，BC=8，∠C的平分线交AD于E，交BA的延长线于F，则AE+AF的值等于（）A．2 B．3 C．4 D．63．如图，CD、BD平分∠BCA及∠ABC，EF过D点且EF∥BC，AB＝8，AC＝6 。

则△AEF的周长是______ 4.（2013泰安）如图，在平行四边形ABCD中，AB=4，∠BAD的平分线与BC的延长线交于点E，与DC 交于点F，且点F为边DC的中点，DG⊥AE，垂足为G，若DG=1，则AE的边长为（）A．2B．4C．4 D．85.（2013菏泽）如图所示，在△ABC中，BC=6，E、F分别是AB、AC的中点，动点P在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当CQ=3CE时，EP+BP= ．6.如图，正方形ABCD中，AB＝6，点E在边C D上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG＝GC；③AG∥CF；④S△FGC＝3．其中正确结论的个数是( )A．1 B．2 C．3 D．47.已知：□ABCD,BE平分∠ABC, CF平分∠BCD,BE、CF分别交AD于E、F，BE与CF交于点G．(1)求证：BE⊥CF．(2)若AB=5，BC=8，求EF的长．8.（2013•张家界）如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F.求证：OE=OF；9.（2013泰安）如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点，（1）求证：AC2=AB•AD；（2）求证：CE∥AD；10.已知：△ABC，AB＝AC，AE是外角∠BAD的平分线，点D为BC的中点，DE∥AC交AE于E,连接BE.求证：四边形AEBD是矩形. 11.（2017.岱岳区）如图，已知一次函数y=23x-3与反比例函数y=xk的图象相交于点A（4，n），与X 轴相交于点B.（1）求反比例函数的表达式；（2）将线段AB沿X轴向右平移5个单位到DC，设DC与双曲线交于点E，求点E到x轴的距离.。

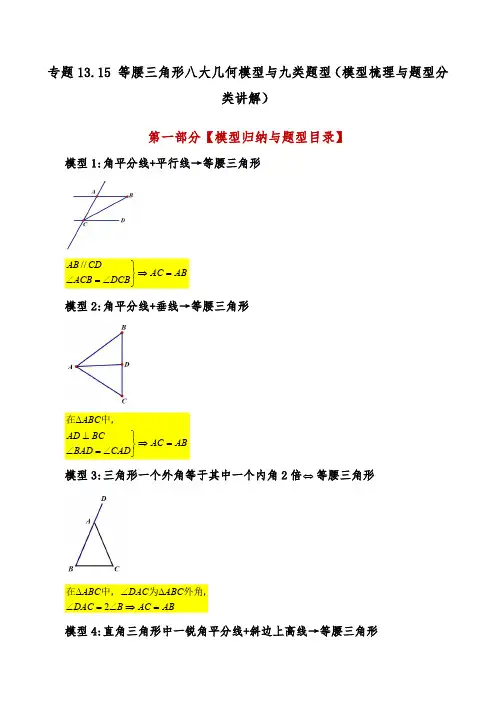
专题13.15等腰三角形八大几何模型与九类题型（模型梳理与题型分类讲解）第一部分【模型归纳与题型目录】模型1:角平分线+平行线→等腰三角形AB AC DCB ACB CDAB =⇒⎭⎬⎫∠=∠//模型2:角平分线+垂线→等腰三角形AB AC CAD BAD BCAD ABC =⇒⎭⎬⎫∠=∠⊥∆中，在模型3:三角形一个外角等于其中一个内角2倍⇔等腰三角形ABAC B DAC ABC DAC ABC =⇒∠=∠∆∠∆2外角，为中，在模型4:直角三角形中一锐角平分线+斜边上高线→等腰三角形CE CD CBD ABD AB CH ACB ABC =⇒⎭⎬⎫∠=∠⊥=∠∆,900中，在模型5:等边三角形中含定角问题60=∠⇒=∆AFE CE BD AC BC E D ABC 上的两个动点、是、中，在等边模型6:等边三角形中含“手拉手”AEBD AE BD DCE ABC =⇒∆∆、中，连接和等边在等边模型7:倍半角+角平分线→等腰三角形DC DB CBD ABD ACB ABC ACB ABC =⇒⎭⎬⎫∠=∠∠=∠=∠∆2900中，在模型8:倍长中线构造等腰三角形题型目录【题型1】角平分线+平行线→等腰三角形 (3)【题型2】角平分线+垂线（中线）→等腰三角形 (4)【题型3】三角形一个外角等于其中一个内角2倍⇔等腰三角形 (4)【题型4】直角三角形中一锐角平分线+斜边上高线→等腰三角形 (5)【题型5】等边三角形中含定角问题 (6)【题型6】等边三角形中含“手拉手” (7)【题型7】倍半角+角平分线→等腰三角形 (8)【题型8】倍长中线构造等腰三角形 (9)【题型9】拓展延伸 (9)第二部分【题型展示与方法点拨】【题型1】角平分线+平行线→等腰三角形【例1】（2024九年级下·浙江·专题练习）如图，在ABC V 中，AD 平分BAC ∠，AD BD ⊥于点D ，DE AC ∥交AB 于点E ，若8AB =，则DE =．【变式1】（2024·湖南娄底·模拟预测）如图，在ABC V 中，AD 平分CAB ∠，ED AB ∥．若ED CD =，15EAD ∠=︒，则ADB ∠等于（）A ．75︒B ．60︒C ．45︒D ．90︒【变式2】（23-24八年级上·天津滨海新·期中）如图，在ABC V 中，ACB ∠的平分线交AB 于点E ，CF 平分ACD ∠，且EF BC ∥交AC 于点G ，若5cm CG =，则EF =cm ．【题型2】角平分线+垂线→等腰三角形【例2】（23-24八年级上·福建龙岩·阶段练习）如图，在ABC V 中，CD 平分ACB ∠，CD BD ⊥，垂足为D ，180A CBD ∠+∠=︒，若5BD =，则AB 的长为（）A ．7B ．8C ．9D ．10【变式1】（23-24八年级上·黑龙江哈尔滨·期中）如图，D 为ABC V 内一点，CD 平分ACB ∠，BE CD ⊥，垂足为D ，交AC 于点E ，A ABE ∠=∠，11AC =，7BC =，则BD 的长为（）A ．1B ．1.5C ．2D ．2.5【变式2】（23-24八年级上·四川宜宾·期末）如图，CE 平分ACB ∠且CE DB ⊥于E ，DAB DBA ∠=∠，若14AC =，CDB △的周长为20，则DB 的长为．【题型3】三角形一个外角等于其中一个内角2倍⇔等腰三角形【例3】（23-24八年级上·吉林长春·期中）如图，在1ABA △中，1AB A B =，20B ∠=︒．在1A B 上取一点C ，延长1AA 到点2A ，使121A A AC =，连结2A C ；在2A C 上取一点D ，延长12AA 到点3A ，使232A A A D =，连结3A D ；……，按此操作进行下去，在以点5A 为顶角顶点的等腰三角形的底角的度数为（）A ．20︒B ．10︒C ．5︒D ．2.5︒【变式1】（23-24八年级上·江苏盐城·期中）如图，在ABC V 中，BD BC =，AE AC =，100ACB ∠=︒，则DCE ∠的大小为．【变式2】（23-24八年级上·全国·单元测试）如图，在ABC V 中，AB AC =，36A ∠= ，BD 平分ABC ∠交AC 于点D ，DE AB ∥交BC 于点E ，EF BD ∥交CD 于点F ，则图中等腰三角形共有（）A ．5个B ．6个C ．7个D ．8个【题型4】直角三角形中一锐角平分线+斜边上高线→等腰三角形【例4】（21-22八年级上·黑龙江哈尔滨·期中）如图，在ABC V 中，90BAC ∠=︒，30C ∠=︒，高AD 与角平分线BE 相交于点F ．（1）求证：AEF △是等边三角形；（2）若2AE =，求AD 的长度．【变式1】（24-25八年级上·全国·假期作业）如图，在ABC V 中，90ACB ∠=︒，CD 是AB 边上的高，AE 是BAC ∠的角平分线，AE 与CD 交于点F ，求证：CEF △是等腰三角形．【变式2】（22-23八年级下·湖南永州·期末）如图，ABC V 中，90BAC AD BC ABC ∠=︒⊥∠，，的平分线BE 交AD 于点F ，AG 平分DAC ∠．给出下列结论：①BAD C ∠=∠；②AEF AFE ∠=∠；③EBC C ∠=∠；④AG EF ⊥；⑤AB GB =．正确结论有（）个.A ．2B ．3C ．4D ．5【题型5】等边三角形中含定角问题【例5】（2024七年级下·上海·专题练习）如图，等边ABC V 中，=AD CE ，BD 和AE 相交于F ，BG AE ⊥垂足为G ，求FBG ∠的度数．【变式1】（23-24八年级下·河南郑州·期末）已知：如图，点D ，E 分别是等边三角形ABC 的两边AB AC ，上的点，且=AD CE .（1）求证：ADC CEB △≌△；（2）求BPC ∠的度数.【变式2】（2024·浙江杭州·二模）如图，ABC V 是等边三角形，D ，E 分别是AC ，BC 边上的点，且=AD CE ，连接BD ，AE 相交于点F ，则下列说法正确的是（）①ABD CAE ≌ ；②60BFE ∠=︒；A ．①B ．②C ．①②D ．都错【题型6】等边三角形中含“手拉手”【例6】（23-24八年级下·陕西西安·阶段练习）如图所示，A 、C 、B 三点共线，DAC △与EBC 都是等边三角形，AE BD 、相交于点P ，且分别与CD CE 、交于点M ，N ．（1）求证：ACE DCBV V ≌（2）求APD ∠的度数【变式1】（2024·重庆南岸·模拟预测）如图，,ABC CDE △△都是等边三角形，将CDE 绕点C 旋转，使得点,,A D E 在同一直线上，连接BE ．若1,4BE AE ==，则CE 的长是．【变式2】（23-24八年级上·福建南平·期末）如图，ABC V 和ADC △都是等边三角形，点E ，F 分别在边BC 和CD 上，且60EAF ∠=︒，若AEF △的周长最小时，则BAE ∠的大小是．【题型7】倍半角→等腰三角形【例7】（22-23八年级上·北京·期中）如图，在ABC V 中，90ABC ∠=︒，D 为AB 上一个动点．（1）已知2A BCD ∠=∠，求证：2AD AC AB +=．下面是两位同学分享的思路：小快同学：从求证目标出发，倍长AB 到E ，即2AE AB =，又AE AD DE =+，则只需证DE AC =．小乐同学：从已知条件角的关系出发，发现若将BCD △关于直线BC 对称得到BCF V ，则可证ACF △为等腰三角形．请你选择一种思路，完成证明（2）已知AB BD AC +=，ACD α∠=，请直接写出A ∠的大小（用含α式子表示）．【变式1】（23-24八年级上·黑龙江哈尔滨·期末）如图，ABC V 中，2C B ∠=∠，,AD AE 分别为ABC V 的高，角平分线，下列四个结论：①AC CD BD +=；②AC CD AB +=；③AC CE AB +=；④2B DAE ∠=∠．其中所有正确结论的序号是．【题型8】倍长中线构造等腰三角形模型【例8】（23-24八年级上·湖北武汉·期中）如图，A 是ABC 的中线，E 是A 上一点，BE 交AC 于F ，若EF AF =，8BE =，5CF =，则EF 的长度为（）A ．1.5B ．2C ．2.5D ．3【变式】（22-23八年级上·湖北武汉·期中）如图，在ABC V 中，D 是BC 的中点，E 是AD 上一点，BE AC =，BE 的延长线交AC 于点F ，若60ACB ∠=︒，44DAC ∠=︒，则求FBC ∠的度数为．第三部分【拓展延伸】【题型9】拓展延伸【例1】（23-24八年级上·北京·期末）如图，ABC V 中，BF CF 、分别平分ABC ∠和ACB ∠，过点F 作DE BC ∥交AB 于点D ，交AC 于点E ，那么下列结论：①DFB DBF ∠=∠；②EFC 为等腰三角形；③ADE V 的周长等于BFC △的周长；④1902BFC A ∠∠=+ ．其中正确的是【例2】（23-24八年级上·上海普陀·期末）【图形新发现】小普同学发现：如果一个三角形的一条角平分线与一条中线互相垂直，那么这个三角形的某两条边必有倍半关系．如图1，已知在ABC V 中，BD 是ABC V 的角平分线，AE 是ABC V 的中线，AE BD ⊥，垂足为点F ．（1）根据图1，写出ABC V 中小普同学所发现的结论，并给出证明；【图形再探究】现将小普同学所研究的三角形称为“线垂”三角形，并将被这条内角平分线所平分的内角叫做“分角”．下面我们跟着小普同学再探究：（2）在如图1中，“线垂”三角形ABC 是否可以是直角三角形？如果可以，求DBC ∠的度数；如果不可以，请说明理由；（3）已知线段MN ，是否存在一点P ，使得以MN 为一边的“线垂”三角形PMN 为等腰三角形？如果存在，请在图2中用直尺和圆规做出PMN ∠为“分角”的“线垂”等腰三角形PMN （不写作法，仅保留作图痕迹，在图中清楚地标注出点P ），并用文字语言归纳表述成一条与“线垂”等腰三角形的边或角有关的真命题；如果不存在，请说明理由．。

中考常考几何模型专题16 角平分线四大模型1、角平分线上的点向两边作垂线如图，P 是∠MON 的平分线上一点，过点 P 作 PA⊥OM 于点 A，PB⊥ON 于点 B。

结论：PB=PA。

2、截取构造对称全等如图，P 是∠MON 的平分线上一点，点 A 是射线 OM 上任意一点，在 ON上截取 OB=OA，连接 PB。

结论：△OPB≌△OPA。

3、角平分线+垂线构造等腰三角形如图，P 是∠MO 的平分线上一点，AP⊥OP 于 P 点，延长 AP 于点 B。

结论：△AOB 是等腰三角形。

4、角平分线+平行线如图，P 是∠MO 的平分线上一点，过点 P 作 PQ∥ON，交 OM 于点 Q。

结论：△POQ 是等腰三角形。

模型精练：1．（2019•东平县二模）如图，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P，若∠BPC＝40°，则∠CAP＝（）A．40°B．45°C．50°D．60°2．（2019•桂平市期末）如图，在△ABC中，∠C＝90°，AD平分∠CAB，BC＝12cm，BD＝8cm，那么点D到直线AB的距离是（）A．2cm B．4cm C．6cm D．10cm3．（2020•浙江自主招生）如图，在△ABC中，AD是∠A的外角平分线，P是AD上异于A的任意一点，设PB＝m，PC＝n，AB＝c，AC＝b，则（m+n）与（b+c）的大小关系是（）A．m+n＞b+c B．m+n＜b+c C．m+n＝b+c D．无法确定4．（2019•兰山区一模）如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB 于M，交AC于N，若BM+CN＝11，则线段MN的长为．5．如图，已知等腰直角三角形ABC中，AB＝AC，∠BAC＝90°，BF平分∠ABC，CD⊥BD交BF的延长线于点D，试说明：BF＝2CD．6．如图，在△ABC中，∠ABE＝2∠C，AD是∠BAC的平分线，BE⊥AD，垂足为E （1）若∠C＝30°，求证：AB＝2BE．（2）若∠C≠30°，求证：BE=12（AC﹣AB）．7．（2019•沂源县期末）如图，在△ABC中，AB＝AC，∠ABC＝40°，BD是∠ABC的平分线，延长BD至E，使DE＝AD，求证：∠ECA＝40°．8．（2019•临洮县期末）已知△ABC中，AB＝AC，∠A＝108°，BD平分∠ABC，求证：BC＝AC+CD．9．（2019•自贡期中）如图，在四边形ABCD中，BC＞BA，AD＝DC，（1）若BD⊥CD，∠C＝60°，BC＝10，求AD的长；（2）若BD平分∠ABC，求证：∠A+∠C＝180°．10．（2019•宜昌期中）（1）已知：如图1，等腰直角三角形ABC中，∠B＝90°，AD是∠BAC的外角平分线，交CB边的延长线于点D．求证：BD＝AB+AC；（2）对于任意三角形ABC，∠ABC＝2∠C，AD是∠BAC的外角平分线，交CB边的延长线于点D，如图2，请你写出线段AC、AB、BD之间的数量关系并加以证明．11．（2019•潮南区期中）在△ABC中，BD是∠ABC的平分线，AD⊥BD，垂足是D．（1）求证：∠2＝∠1+∠C；（2）若ED∥BC，∠ABD＝28°，求∠ADE的度数．12．（2019•蔡甸区校级月考）如图，在△ABC，AD平分∠BAC，E、F分别在BD、AD上，且DE＝CD，EF＝AC，求证：EF∥AB．13．（2019•崇安区校级月考）如图，在梯形ABCD中，AD∥BC，AE平分∠BAD，BE平分∠ABC，且AE、BE交CD于点E．试说明AD＝AB﹣BC的理由．14．（2019•江夏区校级月考）如图1，AB∥CD，P为AB、CD之间一点（1）若AP平分∠CAB，CP平分∠ACD．求证：AP⊥CP；（2）如图（2），若∠BAP=25∠BAC，∠DCP=25∠ACD，且AE平分∠BAP，CF平分∠DCP，猜想∠E+∠F的结果并且证明你的结论；（3）在（1）的条件下，当∠BAQ=13∠BAP，∠DCQ=13∠DCP，H为AB上一动点，连HQ并延长至K，使∠QKA＝∠QAK，再过点Q作∠CQH的平分线交直线AK于M，问当点H在射线AB上移动时，∠QMK的大小是否变化？若不变，求其值；若变化，求其取值范围．15．（2019•东湖区校级月考）（1）如图1，已知：在△ABC中，AB＝AC＝10，BD平分∠ABC，CD平分∠ACB，过点D作EF∥BC，分别交AB、AC于E、F两点，则图中共有个等腰三角形；EF与BE、CF之间的数量关系是，△AEF的周长是（2）如图2，若将（1）中“△ABC中，AB＝AC＝10”改为“若△ABC为不等边三角形，AB＝8，AC ＝10”其余条件不变，则图中共有个等腰三角形；EF与BE、CF之间的数量关系是什么？证明你的结论，并求出△AEF的周长（3）已知：如图3，D在△ABC外，AB＞AC，且BD平分∠ABC，CD平分△ABC的外角∠ACG，过点D作DE∥BC，分别交AB、AC于E、F两点，则EF与BE、CF之间又有何数量关系呢？直接写出结论不证明．中考常考几何模型专题16 角平分线四大模型1、角平分线上的点向两边作垂线如图，P 是∠MON 的平分线上一点，过点 P 作 PA⊥OM 于点 A，PB⊥ON 于点 B。

角平分线和平行线出等腰例题角平分线和平行线出等腰例题角平分线和平行线是我们在几何学中经常遇到的概念。

它们是几何学中的基础知识，很多几何问题都离不开这两个概念。

在这篇文档中，我将讨论关于角平分线和平行线出等腰三角形的例题。

例题1：证明：如果一条角平分线与另一条边相交，那么这条角平分线将这个角分成两个相等的小角。

解析：首先，我们假设有一个角ABC，角平分线AD将其分成两个小角BAD和DAC。

我们需要证明角BAD等于角DAC。

根据角平分线的定义，角BAD和角DAC是由角ABC的两边所构成的。

我们可以将角BAD和角DAC的顶点放在一起，形成一个角BAC。

那么，角BAC的两条边AB和AC都是角ABC的边，这意味着角BAC等于角ABC。

然后，我们可以通过角相等的性质来得到结论。

角BAD等于角BAC，而角DAC等于角BAC，所以角BAD等于角DAC。

这样，我们就证明了角平分线将角ABC分成了两个相等的小角。

例题2：证明：如果一条平行线与一个角的两边相交，那么这条平行线将这个角分成两个相等的小角。

解析：给定一个角ABC和一条平行线DE，我们需要证明角ADE等于角BAC。

首先，我们可以通过转角的定义知道角ADE和角BAC 都是由角ABC的两条边所构成的。

我们将角ADE的顶点放在一起，形成一个角ABC。

由于平行线DE与角ABC的两边相交，可以知道平行线DE和线段AC构成了交角。

接下来，我们可以应用平行线的性质。

平行线与一条直线相交时，对应角相等。

所以，角ADE等于角ABC。

最后，我们可以通过角相等的性质得到结论。

角ADE 等于角ABC，而角BAC也等于角ABC，所以角ADE等于角BAC。

这样，我们就证明了平行线将角ABC分成了两个相等的小角。

例题3：证明：如果一条角平分线与一条平行线相交，那么这条平行线将角平分线所分的角分成两个相等的小角。

解析：给定一条角平分线AD和一条平行线BC，我们需要证明角BAD等于角DAC。

由角平分线与平行线构成的等腰三角形在我们学习几何的过程中，有些知识点之间关系密切，往往带有一定的共性,比如当角平分线与平行线同时出现，那么一定会得到等腰三角形.下面通过几例说明“角平分线＋平行线→等腰三角形”的规律，希望同学们能够举一反三，触类旁通，在解题中灵活运用.一、基本图形（分两种情况）：1.平行线平行于角的一边,如图1，OC 平分∠AOB ，CD ∥OB. 则DO=DC,2.平行线平行于角的平分线，如图2，OC 平分∠AOB ，OC ∥BD.则OD=OB.二、应用举例例1.如图3，在△ABC 中，若AD 平分∠BAC ，交BC 于D,DE ∥AB ，则△ADE 是等腰三角形.证明：如图3，∵AD 平分∠BAC ，∴∠BAD ＝∠CAD ，∵DE ∥AB ，∴∠BAD ＝∠ADE ，∴∠CAD ＝∠ADE ，∴AE ＝DE ，即△ADE 为等腰三角形.变式1：如图4，在△ABC 中，AD 平分∠BAC ，交BC 于D,CE ∥AB ，则△ACE 是等腰三角形；变式2：如图5，在△ABC 中，AD 平分∠BAC ，交BC 于D, BE ∥AC ，则△A BE 是等腰三角形.仿例1可以给出证明.例2.如图6，在△ABC 中，AD 平分∠BAC ，交BC 于D,CE ∥AD ，则△ACE 是等腰三角形.证明：∵AD 平分∠ABC ， ∴∠1＝∠2,AEB CD图3图5 AE BCD图4 AEBCD图1图2∵CE ∥AD ，∴∠2＝∠3，∠1＝∠E ， ∴∠3＝∠E ，∴AC ＝CE.变式1：如图7，在△ABC 中，AD 平分∠BAC ，交BC 于D,EF ∥AD ，交AC 于点G ，交BA 延长线于E,则△AEG 是等腰三角形.变式2：如图8，在△ABC 中，若AD 平分∠BAC ，交BC 于D, EF ∥AD ，交BC 于F ,交CA 的延长线于G ，则△AEG 是等腰三角形.这些基本规律在解题中有一定的指导作用.例3.如图9，在△A BC 中，∠ABC 与∠ACB 的平分线交于点D ，过点D 作EF ∥BC 交AB 于E ，交AC 于F ，（1）求证：EF ＝BE ＋CF ．（2）若AB=9,AC=8，求△AEF 的周长.分析：观察图形，看到EF 已被点D 分成了两条线段(DE 和DF)，而条件中恰好具备“角平分线＋平行线”，可得到两个等腰三角形△BDE 和△CDF ，于是可分别证明DE ＝BE ，DF ＝CF 即可.(1)证明：∵BD 平分∠ABC ，∴∠1＝∠2， ∵EF ∥BC ，∴∠3＝∠2， ∴∠1＝∠3，∴BE ＝DE ， 同理DF ＝CF ，∴DE ＋DF ＝BE ＋CF ，即EF ＝BE ＋CF (2)由（1）得：△AEF 的周长 =AE+AF+EF =AE+AF+(BE ＋CF) =AB+AC =9+8 =17.上述两例都是由角平分线、平行线构成的等腰三角形，并且同时出现两个，而这个发现是突破此类问题难点的关键.例4.如图10，在平行四边形ABCD 中，∠ABC 的平分线交AD 于点E ，∠BCD 的平分线交AD 于点F ，BE 、CF 交于点G ，,AEB CD F G图7BCDFE AG 图8)13(AE BCF D 图9)2A EB CD)1)2图6（1）求证:AF=DE,（2）若AB=3，BC=4，FG=1,求∠A 的度数. (3) 若△EFG 为等腰直角三角形,求∠A 的度 数.解：（1）在平行四边形ABCD 中 ∵AD ∥BC, ∴∠2=∠5，又 ∠2=∠5， ∴∠1=∠5，∴AE=AB, 同理可证：DF=CD. ∵AB=CD ∴AE=DF .∵ AF=AE －EF; DE=DF-EF , ∴AF=DE.（2）在平行四边形ABCD 中，设BE 与CF 交于点G,， ∵AB ∥CD ，∴∠ABC+∠BCD=180°，∵BE 平分∠ABC ，CF 平分∠BCD ，∴12,2ABC ∠=∠ 13,2BCD ∠=∠ 123()902ABC BCD ∠+∠==∠+∠=°，∴∠BGC=90°，即BE ⊥CF ； 因为AD=BC=4，DF=DC=3，∴AF=AD-DF=4-3=1; 又AF=AE －EF; ∴1=3-EF , ∴EF=2.又∵FG=1，∴1,2FG EF =∴∠5=30°，∵AE=AB ，∠1=∠5=30°, ∴∠A=120°. （3）由（2）得∠BGC=90°，∴∠EGF=90°,若△EFG 为等腰直角三角形,则∠5=45°，∴∠1=∠5=45°， ∴∠A=90°.评注：①此题关键在于利用角平分线、平行线发现两个等腰三角形，即△ABE 和△DCF,②利用平行四边形的对边相等，分别得到AF=DE=1,③利用平行线的性质得到Rt △BGC ，Rt △EGF , ④如果直角边为斜边的一半则直角边所对的角为30°.例5.已知：如图11,在△ABC 中,AD 平分∠BAC,EF ∥AB 交BC 于E 、交AD 于F ,若DE=DC.求证：EF=AC.证明:过作CM ∥EF ,交AD 的延长线于M ，连结CM ，则∠M=∠3，，ABCDFE G)2)1 4(3(5(图10图11∠EDF=∠CDM ，又 DE=DC. ∴△EDF ≌△C DM ， ∴EF=CM. ∵ EF ∥AB ，∴∠3=∠1，又∠1=∠2，∴ ∠M=∠2，∴AC=CM ， 从而EF= AC.评析：本题的关键在于作通过添加平行线构成以AC(或EF)为腰的等腰三角形，再证EF=CM.通过上述例题，我们发现，尽管每道题目的结论各异，但每道题中都有角平分线、平行线，故都可得等腰三角形这一共性.所以，在学习过程中，要善于发现、总结规律.真正驳清了基本概念，变成一个个知识板块，其本质属性理解透彻，就能收到举一反三，融会贯通的效果.附：参考习题1.如图12，在△ＡＢＣ中，Ｏ是∠ＡＢＣ、∠ＡＣＢ的角平分线的交点，ＯＤ∥ＡＢ，交ＢＣ于点Ｄ，ＯＥ∥ＡＣ，交ＢＣ于点Ｅ，若ＢＣ＝10cm ，求△DOE 的周长,2.如图13，在△ABC 中，∠ABC 的平分线与∠ACB 的外角∠ACP 的平分线交于D 点，过点D 作EF ∥BC ，交AB 于E ，交AC 于F ，求证：EF ＝EB －FC3.如图14：平行四边形ABCD 中，∠ABC 的平分线交AD 于E ，∠BCD 的平分线交AD 于F ，且AB=3，DE=2，（1）求平行四边形ABCD 的周长．（2）求证：BE ⊥CF （3）若CF=2，求BE 的长．.参考答案：1.△DOE 的周长为10cm ； 2.证明略；3.（1）平行四边形ABCD 的周长为16；（2）证明略；（3）BE=22226242BE BN EN =-=-=.AE B COD图12 )1 )2 4(图14A EBCFDP图13。

等腰三角形的典型模板专题练习模型一、角平分线+平行线1、如图，△ABC中，AD是∠BAC的平分线，DE//AB交AC于点E，若DE=7，CE=5，则AC=（）．A. 10B. 11C. 12D. 13答案：C解答：∵△ABC中，AD是∠BAC的平分线，∴∠BAD=∠CAD.∵DE//AB，DE=7，CE=5，∴∠CAD=∠ADE．∴AE=DE=7．∴AC=AE+CE=7+5=12．2、如图，已知在△ABC中，BO平分∠ABC，CO平分∠ACB，且OM//AB，ON//AC，若CB=6，则△OMN的周长是（）．A. 3B. 6C. 9D. 12答案：B解答：∵OM//AB，∴∠ABO=∠BOM，而∠ABO=∠OBM，则∠BOM=∠OBM．∴△OBM为等腰三角形，且OM=BM．同理可证ON=CN．故C△OMN=OM+ON+MN=BM+CN+MN=BC=6．选B.3、如图，在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别为R、S，若AQ=PQ，PR=PS，则这四个结论中正确的有（）．①PA平分∠BAC；②AS=AR；③QP//AR；④△BRP≌△CSP．A. 4个B. 3个C. 2个D. 1个答案：B解答：①PA平分∠BAC.∵PR⊥AB，PS⊥AC，PR=PS，AP=AP，∴△APR≌△APS，∴∠PAR=∠PAS，∴PA平分∠BAC.②由①中的全等也可得AS=AR．③∵AQ=PQ，∴∠1=∠APQ，∴∠PQS=∠1+∠APQ=2∠1，又∵PA平分∠BAC，∴∠BAC=2∠1，∴∠PQS=∠BAC，∴PQ//AR．④∵PR⊥AB，PS⊥AC，∴∠BRP=∠CSP，∵PR=PS，∴△BRP不一定全等于△CSP（只具备一角一边的两三角形不一定全等）．选B.4、如图，在△ABC中∠ABC、∠ACB的角平分线交于点O，MN过点O，且MN//BC，分别交AB、AC于点M、N，若MN=5cm，CN=2cm，则BM=______cm．答案：3解答：∵BO平分∠ABC，∴∠ABO=∠CBO．∵MN//BC.∴∠MOB=∠OBC，∴∠ABO=∠MOB，∴BM=OM．同理，ON=CN，∴BM=MN-CN=5-2=3cm．故答案为：3．5、如图，∠ABC=50°，BD平分∠ABC，过D作DE//AB交BC于点E，若点F在AB上，且满足DF=DE，则∠DFB的度数为______．答案：130°或50°解答：如图，DF=DF’=DE．∵BD平分∠ABC，由图形的对称性可知：△BDEmathbf△BDF，∴∠DFB=∠DEB.∵DE//AB，∠ABC=50°，∴∠DEB=180°-50°=130°．∴∠DFB=130°．当点F位于点F’处时，∵DF=DF’，∴∠DF’B=∠DFF’=50°，故答案是：50°或130°．6、如图，在△ABC中，BE、CE分别是∠ABC和∠ACB的平分线，过点E作DF//BC交AB于D，交AC于F，若AB=4，AC=3，则△ADF周长为______．答案：7解答：∵BE，CE为∠ABC和∠ACB的平分线，∴∠1=∠2，∠5=∠6，∵DF//BC，∴∠2=∠3，∠4=∠6，∴∠1=∠3，∠4=∠5，∴DB=DE，FE=FC，∴C△ADF=AD+DF+AF=AD+AF+DE+EF=AD+AF+DB+FC=AB+AC=7．7、已知如图：△ABC中，AB=AC，∠B、∠C的平分线相较于点O，过点O作EF//BC分别交AB、AC于E、F．（1）写出线段EF与BE、CF之间的数量关系？（不证明）（2）若AB≠AC，其他条件不变，如图，图中线段EF与BE、CF间是否存在（1）中数量关系？请说明理由．（3）若△ABC中，AB≠AC，∠B的平分线与三角形外角∠ACD的平分线CO交于O，过点O 作OE//BC交AB于E，交AC于F，如图，这时图中线段EF与BE、CF间存在什么数量关系？请说明理由．答案：（1）EF=BE+CF．（2）仍然有EF=BE+CF．（3）EF=BE-CF．解答：（1）EF=BE+CF．（2）仍然有EF=BE+CF，理由如下：∵EF//BC，∴∠EOB=∠OBC，∵BO平分∠ABC，∴∠EBO=∠OBC，∴∠EOB=∠EBO，∴OE=BE，同理OF=FC，∴EF=EO+OF=BE+CF．（3）EF=BE-CF，理由如下：∵OE//BC，∴∠EOC=∠OCD，∵CO平分∠ACD，∴∠FCO=∠OCD，∴∠FCO=∠FOC，∴OF=CF，同理可得到BE=EO，∴EF=EO-FO=BE-CF．8、如图，在△ABC中，AB=BC，∠ABC的平分线BF与∠ACB的外角平分线交于点F，过点F 作DF//BC，交AB于点D，交AC于点E．（1）图中除△ABC之外，还有几个等腰三角形，请分别写出来．（2）若EC=6，BD=8，求DE的长．答案：（1）△DAE，△DBF，△ECF是等腰三角形．______（2）2．解答：（1）有题意可知∠ABF=∠CBF=∠DFB，∠A=∠DEA=∠BCA，∠DFC=∠ACF=∠FCG，∴△DAE，△DBF，△ECF是等腰三角形．______（2）∵DF//BC，∴∠DFB=∠FBC，又∵BF是∠ABC的角平分线，∴∠ABF=∠CBF，∴∠DBF=∠DFB，∴△DBF是等腰三角形，∴DF=DB=8．又DF//BC，∴∠DFC=∠FCG，又∵CF是∠ACG的角平分线，∴∠FCG=∠DFC，∴∠ACF=∠DFC，∴△ECF是等腰三角形，∴EF=EC=6，∴DE=DF-EF=8-6=2．模型二、角平分线+垂线9、如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为点D，交AC于点E，∠A=∠ABE，AC=5，BC=3，则BD的长为（）．A. 1B. 1.5C. 2D. 2.5 答案：A解答：∵CD平分∠ACB，BE⊥CD，∴BC=CE．又∵∠A=∠ABE，∴AE=BE．∴BD=12BE=12AE=12（AC-BC）．∵AC=5，BC=3，∴BD=12（5-3）=1．选A.10、在△ABC中，∠ACB=90°，AC=BC，线段AD是△ABC的角平分线，过点B作AD的垂线交AD的延长线于点E，若BE=4，则AD=______．答案：8解答：延长AC，与BE交于点F，∵∠ADC+∠CAD=90°，∠EBD+∠BDE=90°，∠BDE=∠ADC，∴∠EBD =∠DAC ，在△CBF 和△CAD 中，90EBD DAC BC AC ACD BCF ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ∴△CBF ≌△CAD （ASA ），∴AD =BF ，∵△ABF 中，AE ⊥BF ，∠BAE =∠FAE ，∴△ABF 是等腰三角形，∴BE =EF ，∴AD =2BE =8．故答案为：8．11、如图，在△ABC 中，BE 是∠ABC 的角平分线，AD ⊥BE ，垂足为D. 求证：∠2=∠1+∠C.答案：证明见解答．解答：如图，延长AD 交BC 于F ．∵∠ABD =∠FBD ，BD =BD ，∠ADB =∠FDB =90°，∴Rt △ABD ≌Rt △FBD.于是∠2=∠DFB.∵∠DFB =∠1+∠C ，∴∠2=∠1+∠C.12、如图，△ABC 中，AD 平分∠BAC ，CD ⊥AD 与点D ，∠ACD =2∠B ，若CD =8，AB =26，求AC 的长．答案：AC =10．解答：如图，延长CD 交AB 于点E ．∵AD 平分∠BAC ，∴∠1=∠2．∵CD ⊥AD ，∴∠ADE =∠ADC =90°∵在△ADE 和△ADC 中12AD ADADE ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ADE ≌△ADC （ASA ）．∴DE =CD =8．∠AEC =∠ACD.又∵∠ACD =2∠B ，∠AED =∠B +∠ECB.∴∠B =∠ECB.∴BE =CE =16，∴AC =AE =AB -BE =10．模型三、垂直平分线13、如图，在△ABC中，∠A=105°，AC的垂直平分线MN交BC于点E，AB+BE=BC，则∠B 的度数是（）．A. 45°B. 50°C. 55°D. 60°答案：B解答：连接AE，∵MN垂直平分AC，∴AE=CE，∴∠EAC=∠C，∴∠AEB=2∠C，又∵AB+BE=BC，∴AB=AE=CE，∴∠ABE=∠AEB=2∠C，又∵∠A=105°，∴∠B=1051803︒︒-×2=50°．14、如图，等腰△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，∠DBC=15°，则∠A 的度数是（）．A. 35°B. 40°C. 50°D. 55°答案：C解答：∵DM 是AB 的垂直平分线，∴AD =BD ，∴∠ABD =∠A ，∵等腰△ABC 中，AB =AC ，∴∠ABC =∠C =1802A ∠︒-， ∴∠DBC =∠ABC -∠ABD =1802A ∠︒--∠A =15°， 解得：∠A =50°，选C.15、如图，在△ABC 中，AB =AC ，∠A =20°，线段AB 的垂直平分线交AB 于D ，交AC 于E ，连接BE ，则∠CBE 为______度．答案：60解答：∵AB =AC ，∠A =20°，∴∠ABC =∠C =80°．∵线段AB 的垂直平分线交AB 于D ，∴AE =BE ，∴∠ABE =∠A =20°，∴∠CBE =∠ABC -∠ABE =80°-20°=60°．16、如图，Rt △ABC 中，∠ACB =90°，∠A =15°，AB 的垂直平分线与AC 交于点D ，与AB 交于点E ，连接BD ，若AD =14，则BC 的长为______．答案：7解答：∵DE 是AB 的垂直平分线，∴AD =BD =14，∴∠A=∠ABD=15°，∴∠BDC=∠A+∠ABD=15°+15°=30°，在Rt△BCD中，BC=12BD=12×14=7．17、如图，在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F，CF=3，则BF的长为______．答案：6解答：连接AF，∵AB=AC，∠BAC=120°，∴∠B=∠C=1201802︒︒-=30°，∵AC的垂直平分线EF交AC于点E，交BC于点F，∴CF=AF，∴∠FAC=∠C=30°，∴∠BAF=∠BAC-∠FAC=120°-30°=90°，在Rt△ABF中，∠B=30°，∴BF=2AF，∴BF=2CF=6．18、在△ABC中，∠ACB=90°，∠A=30°，AB的垂直平分线分别交AB和AC于点D、E．（1）求证：AE=2CE．（2）连接CD、请判断△BCD的形状，并说明理由．答案：（1）证明见解答．（2）△DBC为等边三角形．解答：（1）连BE，∵ED垂直平分AB，∴EA=EB，∴∠EAB=∠EBA，∵∠A=30°，∠C=90°，∴∠ABC=60°，∠EBC=30°，∵在Rt△EBC中，∠EBC=30°，∴BE=2EC，∵EB=EA，∴AE=2CE．（2）∵ED垂直平分AB，∴AD=DB，∵在Rt△ACB中，∠C=90°，∴CD=BD，又∵∠ABC=60°，∴△DBC为等边三角形．19、如图，在△ABC中，DE，FG分别是AB，AC的垂直平分线，连接AE，AF，已知∠BAC=80°，请运用所学知识，确定∠EAF的度数．答案：20°．解答：在△ABC中，∠BAC=80°，∴∠B+∠C=180°-∠BAC=100°，∵DE是AB的垂直平分线，∴EB=EA，∴∠BAE=∠B，同理可得∠CAF=∠C，∴∠EAF=∠BAE+∠CAF-∠BAC=∠B+∠C-∠BAC=20°．模型四、倍角20、如图，△ABC中，AD⊥BC于D，∠B=2∠C，求证：AB+BD=CD答案：解答：延长CB到点E，使得BE=AB，连接AE得△ABE为等腰三角形，∴∠1=∠E，∠B=2∠E∵∠B=2∠C∴∠C=∠E∴△ACE为等腰三角形∵AD⊥BC∴CD=DE∴AB+BD=BE+BD=DE=CD21、如图，在△ABC中，∠ACB=2∠B，BC=2AC. 求证：∠A=90°．答案：解答：作CD平分∠ACB交AB于D，过D作DE⊥BC于E，∵∠ACB=2∠B，CD平分∠ACB∴∠B=∠BCD即△DBC是等腰三角形∵DE⊥BC∴BC=2CE又BC=2AC∴AC=CE易证≌△ACD≌△ECD（SAS）∴∠A=∠DEC=90°。

专题17 等腰三角形的判定例题与求解【例1】如图，在△ABC 中，AB =7，AC =11，点M 是BC 的中点，AD 是∠BAC 的平分线，MF ∥AD ，则CF 的长为____________．解题思路：角平分线+平行线易构造等腰三角形，解题的关键是利用条件“中点M ”．【例2】如图，在△ABC 中，∠B =2∠C ，则AC 与2AB 之间的关系是（ ） A ．AC ＞2AB B ．AC ＝2AB C ．AC ≤2AB D ．AC ＜2AB解题思路：如何条件∠B =2∠C ，如何得到2AB ，这是解本题的关键．【例3】两个全等的含300，600角的三角板ADE 和三角板ABC ，如图所示放置，E 、A 、C 三点在一条直线上，连结BD ，取BD 中点M ，连结ME ，MC ，试判断△EMC 的形状，并说明理由．（山东省中考试题）解题思路：从△ADE ≌△BAC 出发，先确定△ADB 的形状，为判断△EMC 的形状奠定基础．【例4】如图，已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE =AC ，延长BE 交AC 于F ，求证：AF =EF ．解题思路：只需证明∠F AE =∠AEF ，利用中线倍长，构造全等三角形、等腰三角形．ABCABDM FCABCMDE【例5】如图，在等腰△ABC 中，AB =AC ，∠A =200，在边AB 上取点D ，使AD =BC ，求∠BDC 度数．解题思路：由条件知底角为300，这些角并不是特殊角，但它们的差却为600，600使我们联想到等边三角形，由此找到切入口．如图1，以BC 为边在△ABC 内作等边△BCO ；如图②，以AC 为边作等边△ACE ．能力训练A 级1．已知△ABC 为等腰三角形，由顶点A 所引BC 边的高线恰等于BC 边长的一半，则 ∠BAC =__________．2．如图，在Rt △ABC 中，∠C =900，∠ABC =660，△ABC 以点C 为中点旋转到△A ′B ′C 的位置，顶点B 在斜边A ′B ′上，A ′C 与AB 相交于D ，则∠BDC =_________．3．如图，△ABC 是边长为6的等边三角形，DE ⊥BC 于E ，EF ⊥AC 于F ，FD ⊥AB 于D ，则AD =_______．4．如图，一个六边形的六个内角都是1200，其连续四边的长依次是1cm ，9cm ，9cm ，5cm ，那么这个六边形的周长是____________cm ．5．如图，△ABC 中，AB =AC ，∠B =360，D 、E 是BC 上两点，使∠ADE =∠AED =2∠BAD ，则图中等腰三角形共有（ ）A ．3个B ．4个C ．5个D ．6个6．若△ABC 的三边长是a ，b ，c ，且满足44422a b c b c =+-，44422b ac a c =+-，BCA D图2B CA D图1O ACDB B ′A ′(第2题)ABCDE F (第3题)(第4题)9915EA BDCFBCAD44422c a b a b =+-，则△ABC （）A ．钝角三角形B ．直角三角形C ．等腰直角三角形D ．等边三角形7．等腰三角形一腰上的高等于该三角形某一条边的长度的一半，则其顶角等于（ ） A ．300 B ．300或1500 C ．1200或1500 D ．300或1200或15008．如图，已知Rt △ABC 中，∠C =900，∠A =300，在直线BC 或AC 上取一点P ，使得△P AB 是等腰三角形，则符合条件的P 点有（ ）A ．2个B ．4个C ．6个D ．8个第5题图 第8题图 第9题图9．如图在等腰Rt △ABC 中，∠ACB =900，D 为BC 中点，DE ⊥AB ，垂足为E ，过点B 作BF ∥AC 交DE 的延长线于点F ，连接CF 交AD 于G ．⑴ 求证：AD ⊥CF ；⑵ 连结AF ，度判断△ACF 的形状，并说明理由．10．如图，△ABC 中，AD ⊥BC 于D ，∠B =2∠C ，求证：AB +BD =CD ．11．如图，已知△ABC 是等边三角形，E 是AC 延长线上一点，选择一点D ，使得△CDE 是等边三角形，如果M 是线段AD 的中点，N 是线段BE 的中点，求证：△CMN 是等边三角形．12．如图1，Rt △ABC 中，∠ACB =900，CD ⊥AB ，垂足为D ，AF 平分∠CAB ，交CD 于点E ，交CB 于点F ．ACDBACD EBCABCADFG E AC ENMBD⑴ 求证：CE =CF ；⑵ 将图1中的△ADE 沿AB 向右平移到△A ′D ′E 的位置，使点E ′落在BC 边上，其他条件不变，如图2所示，试猜想：BE ′与CF 有怎样的数量关系？请证明你的结论．B 级1．如图，△ABC 中，AD 平分∠BAC ，AB +BD =AC ，则∠B ：∠C 的值=__________．2．如图，△ABC 的两边AB 、AC 的垂直平分线分别交BC 于D 、E ，若∠BAC +∠DAE =1500，则∠BAC 的度数是____________．3．在等边△ABC 所在平面内求一点P ，使△P AB 、△PBC 、△P AC 都是等腰三角形，具有这样性质的点P 有_________个．4．如图，在△ABC 中，∠ABC =600，∠ACB =450，AD 、CF 都是高，相交于P ，角平分线BE 分别交AD 、CF 于Q 、S ，则图中的等腰三角形的个数是（ ）A ．2B ．3C ．4D ．55．如图，在五边形ABCDE 中，∠A =∠B =1200，EA =AB =BC =12DC =12DE ，则∠D =（ ） A ．300B ．450C ．600D ．67.506．如图，∠MAN =160，A 1点在AM 上，在AN 上取一点A 2，使A 2A 1=AA 1，再在AM 上取一点A 3，使A 3A 2=A 2A 1，如此一直作下去，到不能再作为止，那么作出的最后一点是（ ）A ．A 5B ．A 6C ．A 7D ．A 8 7．若P 为△ABC 所在平面内一点，且∠APB =∠BPC =∠CP A =1200，则点P 叫作△ABC 的费尔马点，如图1．A BDFE C图1A B D FEC图2A ′E ′D ′AB C D(第1题)(第2题)ABD E CA BD CEF PQS (第4题)A B CED第5题AA 1NMA 2A 3(第6题)⑴若点P 为锐角△ABC 的费尔马点，且∠ABC =600，P A =3，PC =4，则PB 的值为_____．⑵如图2，在锐角△ABC 外侧作等边△ACB ′，连结BB ′．求证：BB ′过△ABC 的费尔马点P ，且BB ′=P A +PB +PC ．8．如图，△ABC 中，∠BAC =600，∠ACB =400，P 、Q 分别在BC 、AC 上，并且AP 、BQ 分别是∠BAC 、∠ABC 的角平分线，求证：BQ +AQ =AB +BP ．9．如图，在△ABC 中，AD 是∠BAC 的平分线，M 是BC 的中点，过M 作ME ∥AD 交BA 延长线于E ，交AC 于F ，求证：BE =CF =12(AB +AC )．10．在等边△ABC 的边BC 上任取一点D ，作∠DAE =600，DE 交∠C 的外角平分线于E ，那么△ADE 是什么三角形？证明你的结论．ABPQCA BPACBB ′图1图2ABD MFE。

利用平行线构造等腰三角形知识纵横：等腰三角形有丰富的性质，这些性质为我们解几何题提供了新的理论依据，所以寻找发现等腰三角形是解一些几何题的关键。

常用构造等腰三角形方法有：①.“角平分线+ 平行线”②.“角平分线+垂线”③.“垂直平分线”④.“三角形中角的2倍关系”一．作腰的平行线构造等腰三角形基本图形：如图，若AB=AC，DE//AC ,则BDE为等腰三角形例1.如图，△ABC中，AB=AC，点D为AB上一点，延长AC至E，使CE=BD，连接DE交BC于F，求证：DF=EF练习1.如图，等边三角形ABC中，AD=CE，DE交AC于点F，求证DF=EF二．作底边（或高）的平行线构造等腰三角形例2.如图，在△ABC中，AB=AC，点E在AC上，点D在BA的延长线上，且AD=AE，连接DE，求证：DE⊥BC练习2.如图，已知：BAC CBF ∠∠与的平分线相交于P ，联结CP ，分别过点B 、C 作PC 、PB 的垂线交AC 、AB 的延长线于E 、F ，G 、H 为垂足。

求证：BF=CE三．利用“角平分线+平行线”构造等腰三角形例3. 如图，BD 平分∠ABC 交AC 于点D ，点E 为CD 上一点，且AD=DE ，EF//BC 交BD 于点F ，求证：AB=EF 。

练习3.．如图，△ABC 中，CE 为△ABC 的角平分线，交AB 于点E ，过点E 作EF//BC 交AC 于点O ，交△ABC 外角∠ACD 的平分线于点F ，求证：OE ＝OF练习4. 如图，AF 是△ABC 的角平分线，BD ⊥AF 交AF 的延长线于D ，DE ∥AC•交AB 于E ，求证：AE=BE ．四．等腰直角三角形中的双垂线构造基本图形例4，如图，在四边形ABCE中，AB=BC，AB⊥BC，CE⊥AE，BD⊥AE于点D，求证：BD - CE=AD练习5.如图，在△ABC中，AB=AC，∠BAC=90°，D为BC上一点，过点D作DE⊥AD，且DE=AD，连接BE，求∠DBE的度数。

初中数学经典几何模型专题04 角平分线模型在三角形中的应用在初中几何证明中，常会遇到与角平分线有关的问题。

不少同学遇到这类问题时，不清楚应该怎样去作辅助线。

实际上这类问题是有章可循的，其策略是:明确辅助线作用，记清相应模型辅助线作法，理解作辅助线以后的目的。

能做到这三点，就能在解题时得心应手。

【知识总结】【模型】一、角平分线垂两边 角平分线+外垂直当已知条件中出现OP 为OAB ∠的角平分线、PM OA ⊥于点M 时，辅助线的作法大都为过点P 作PN OB ⊥即可.即有PM PN =、OMP ∆≌ONP ∆等，利用相关结论解决问题.【模型】二、角平分线垂中间 角平分线+内垂直当已知条件中出现OP 为AOB ∠的角平分线,PM OP ⊥于点P 时，辅助线的作法大都为延长MP 交OB 于点N 即可.即有OMN ∆是等腰三角形、OP 是三线等，利用相关结论解决问题.【模型】三、角平分线构造轴对称 角平分线+截线段等当已知条件中出现OP 为AOB ∠的角平分线、PM 不具备特殊位置时，辅助线的作法大都为在OB 上截取ON OM =，连结PN 即可.即有OMP ∆≌ONP ∆，利用相关结论解决问题.【模型】四、角平分线加平行线等腰现 角平分线+平行线当已知条件中出现OP 为AOB ∠的角平分线，点P 角平分线上任一点时，辅助线的作法大都为过点P 作PM //OB 或PM //OA 即可.即有OMP ∆是等腰三角形，利用相关结论解决问题.1、如图, ABN CBN ∠=∠, P 为BN 上的一点，并且PD BC ⊥于点D ,2AB BC BD +=,求证：180BAP BCP ∠+∠=︒.2、如图，在ABC ∆中，CD 是ACB ∠的平分线，AD CD ⊥于点D ,DE //BC 交AB 于点E ，求证:EA EB =.3、已知:如图7,2,,AB AC BAD CAD DA DB =∠=∠=，求证:DC AC ⊥.4、如图,AB //CD ,AE 、DE 分别平分BAD ∠和ADC ∠.探究:在线段AD 上是否存在点M ，使得2AD EM =.【基础训练】1、如图所示，在四边形ABCD中，DC//AB，∠DAB=90°，AC⊥BC，AC=BC，∠ABC的平分线交AD，AC于点E、F，则BFEF的值是___________.2、如图，D是△ABC的BC边的中点，AE平分∠BAC，AE⊥CE于点E，且AB =10，AC =16，则DE的长度为______3、如图所示，在△ABC中，BC=6，E、F分别是AB、AC的中点，动点P在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当CQ =13CE时，EP+BP =________.【巩固提升】1、如图，F，G是OA上两点，M，N是OB上两点，且FG =MN，S△PFG=S△PMN，试问点P是否在∠AOB 的平分线上？2、已知：在△ABC中，∠B的平分线和外角∠ACE的平分线相交于D，DG//BC，交AC于F，交AB于G，求证：GF =BG CF.3、在四边形ABCD中，∠ABC是钝角，∠ABC+∠ADC =180°，对角线AC平分∠BAD.（1）求证：BC =CD；（2）若AB +AD =AC，求∠BCD的度数；4、如图，在△ABC中，D、E、F分别为三边的中点，G点在边AB上，△BDG与四边形ACDG的周长相等，设BC =a、AC =b、AB =c.（1）求线段BG的长（2）求证：DG平分∠EDF.5、如图，BA⊥MN，垂足为A，BA=4，点P是射线AN上的一个动点（点P与点A不重合），∠B PC=∠BP A，BC⊥BP，过点C作CD⊥MN，垂足为D，设AP=x.CD的长度是否随着x的变化而变化？若变化，请用含x的代数式表示CD的长度；若不变化，请求出线段CD的长度.6、已知：平面直角坐标系中，四边形OABC的顶点分别为0（0，0）、A（5，0）、B（m，2）、C（m-5，2）.（1）问：是否存在这样的m，使得在边BC上总存在点P，使∠OP A=90°？若存在，求出m的取值范围；若不存在，请说明理由.（2）当∠AOC与∠OAB的平分线的交点Q在边BC上时，求m的值.7、我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”。

角平分线和平行线构成等腰三角形的探究-----李春蕊北京市育英学校一、教材分析：《等腰三角形》是“人教版八年级数学（上）”第十二章第三节的内容。

等腰三角形是一种特殊的三角形，它除了具备一般三角形的所有性质外，还有许多特殊的性质，由于这些特殊性质，使它比一般的三角形应用更广泛。

这一单元的主要内容是等腰三角形的性质和判定，以及等边三角形的相关知识，尤其是等腰三角形的性质和判定，它们是研究等边三角形、证明线段等和角等的重要依据.学情分析：本节课在学生已经学习了轴对称、等腰三角形性质及判定基础上，进一步探究角平分线和平行线形成等腰三角形的问题。

学生具有一定说理能力，整体几何感观比较清晰，在探究活动中，能够根据老师的问题进行有切入的思考。

二、教学目标：（1）掌握角平分线和平行线形成等腰三角形的基本规律；（2）体会研究问题中用到的分类思想，经历由特征图形问题的解决，发展对问题的进一步探究，认识到在几何问题中，位置关系可得出一定数量关系，特殊的数量关系也能推出一定位置关系.（3）通过交流和研讨，使学生在探索的同时获得解决问题的一种方法，提高学生学习数学的兴趣和信心.教学重点：掌握角平分线+平行线能形成等腰三角形这个基本规律，利用这个规律解决等腰三角形方面的有关问题.教学难点：灵活运用角平分线和平行线形成等腰三角形这个基本规律解决有关问题.突出重点方法:观察，思考，证明.突出难点方法:自主探究教学方法：启发与探究相结合教学准备：PPT，课本，作图工具三、教学设计：（一）复习等腰三角形相关知识1、请同学们对等腰三角形的知识要点进行自我回顾：（由学生先进行回顾，教师补充）（二）探究过程问题1：已知∠ABC，BD平分∠ABC，ED//BC.思考：△EBD是等腰三角形吗？解：是；EB=ED发现：无论点D 在BD 上如何运动，△EBD 都是等腰三角形结论：角平分线+平行线 等腰三角形我们在几何证明中，一般不单独研究角，大多数都是借助图形，比如在三角形中研究问题，上面问题如果放在三角形中，我们可以作三角形中一个角的角平分线，然后过角平分线上一点，作这个角的一边的平行线。