平行线及角平分线类相似
- 格式:doc
- 大小:1.81 MB
- 文档页数:22

相似热门题型解题技巧整理类型1 证比例式或等积式的技巧方法指导:证比例式或等积式,若所遇问题中无平行线或相似三角形,则需构造平行线或相似三角形,得到成比例线段;若比例式或等积式中的线段分布在两个三角形或不在两个三角形中,可尝试证这两个三角形相似或先将它们转化到两个三角形中再证两三角形相似,若在两个明显不相似的三角形中,可运用中间比代换.题型1 构造平行线法1.如图,在△ABC 中,D 为A 中点,DF 交AC 于点E ,交BC 的延长线于点F ,求证:AE ·CF =BF ·EC .1.证明:如图,过点C 作CM ∥AB 交DF 于点M . ∵CM ∥AB ,∴△CMF ∽△BDF . ∴BF CF =BD CM. 又∵CM ∥AD ,∴△ADE ∽△CME .∴AE EC =ADCM .∵D 为AB 的中点,∴BD CM =AD CM .∴BF CF =AE EC,即AE ·CF =BF ·EC . 2.如图,已知△ABC 的边AB 上有一点D ,边BC 的延长线上有一点E ,且AD =CE ,DE 交AC 于点F ,试证明:AB ·DF =BC ·EF .2.证明:过点D 作DG ∥BC ,交AC 于点G , ∴△DGF ∽△ECF ,△ADG ∽△ABC . ∴EF DF =CE DG ,AB BC =AD DG. ∵AD =CE ,∴CE DG =AD DG .∴AB BC =EFDF,即AB ·DF =BC ·EF .点拨:过某一点作平行线,构造出“A ”型或“X ”型的基本图形,通过相似三角形转化线段的比,从而解决问题.题型2 三点找三角形相似法1.如图,在▱ABCD 中,E 是AB 延长线上的一点,DE 交BC 于F .求证:DC AE =CFAD .1.证明:∵四边形ABCD 是平行四边形. ∴AE ∥DC ,∠A =∠C .∴∠CDF =∠E , ∴△DAE ∽△FCD ,∴DC AE =CFAD.2.如图,在△ABC 中,∠BAC =90°,M 为BC 的中点,DM ⊥BC 交CA 的延长线于D ,交AB 于E .求证:AM 2=MD ·ME .2.证明:∵DM ⊥BC ,∠BAC =90°, ∴∠B +∠BEM =90°,∠D +∠DEA =90°. ∵∠BEM =∠DEA ,∴∠B =∠D . 又∵M 为BC 的中点,∠BAC =90°,∴BM =AM . ∴∠B =∠BAM .∴∠BAM =∠D .又∵∠AME =∠DMA .∴△AME ∽△DMA . ∴AM MD =MEAM.∴AM 2=MD ·ME .题型3 构造相似三角形法1.如图,在等边三角形ABC 中,点P 是BC 边上任意一点,AP 的垂直平分线分别交AB ,AC 于点M ,N .求证:BP ·CP =BM ·CN .1.证明:如图,连接PM ,PN . ∵MN 是AP 的垂直平分线, ∴MA =MP ,NA =NP . ∴∠1=∠2,∠3=∠4. 又∵△ABC 是等边三角形, ∴∠B =∠C =∠1+∠3=60°. ∴∠2+∠4=60°. ∴∠5+∠6=120°. 又∵∠6+∠7=180°-∠C =120°. ∴∠5=∠7.∴△BPM ∽△CNP . ∴BP CN =BM CP,即BP ·CP =BM ·CN .题型4 等比过渡法1.如图,在△ABC 中,AB =AC ,DE ∥BC ,点F 在边AC 上,DF 与BE 相交于点G ,且∠EDF =∠ABE .求证:(1)△DEF ∽△BDE ; (2)DG ·DF =DB ·EF .1.证明:(1)∵AB =AC ,∴∠ABC =∠ACB .∵DE ∥BC ,∴∠ABC +∠BDE =180°,∠ACB +∠CED =180°,∴∠CED =∠BDE .又∵∠EDF =∠ABE ,∴△DEF ∽△BDE .(2)由△DEF ∽△BDE 得DE BD =EFDE,∴DE 2=DB ·EF .又由△DEF ∽△BDE ,得∠BED =∠DFE .∵∠GDE =∠EDF ,∴△GDE ∽△EDF .∴DG DE =DEDF,∴DE 2=DG ·DF ,∴DG ·DF =DB ·EF .2.如图,CE 是Rt △ABC 斜边上的高,在EC 的延长线上任取一点P ,连接AP ,作BG ⊥AP 于点G ,交CE 于点D .求证:CE 2=DE ·PE .2.证明:∵BG ⊥AP ,PE ⊥AB , ∴∠AEP =∠BED =∠AGB =90°. ∴∠P +∠PAB =90°,∠PAB +∠ABG =90°. ∴∠P =∠ABG .∴△AEP ∽△DEB . ∴AE DE =PEBE,即AE ·BE =PE ·DE . 又∵CE ⊥AB ,∴∠CEA =∠BEC =90°,∴∠CAB +∠ACE =90°. 又∵∠ACB =90°,∴∠CAB +∠CBE =90°. ∴∠ACE =∠CBE .∴△AEC ∽△CEB . ∴AE CE =CEBE,即CE 2=AE ·BE .∴CE 2=DE ·PE . 题型5 两次相似法1.如图,在Rt △ABC 中,AD 是斜边BC 上的高,∠ABC 的平分线BE 交AC 于E ,交AD 于F .求证:BF BE =ABBC .1.证明:易得∠BAC =∠BDF =90°. ∵BE 平分∠ABC ,∴∠ABE =∠DBF , ∴△BDF ∽△BAE ,得BD AB =BFBE.∵∠BAC =∠BDA =90°,∠ABC =∠DBA . ∴△ABC ∽△DBA ,得AB BC =BD AB ,∴BF BE =AB BC.2.如图,在▱ABCD 中,AM ⊥BC ,AN ⊥CD ,垂足分别为M ,N .求证:(1)△AMB ∽△AND ; (2)AM AB =MN AC .2.证明:(1)∵四边形ABCD 为平行四边形.∴∠B =∠D . ∵AM ⊥BC ,AN ⊥CD ,∴∠AMB =∠AND =90°, ∴△AMB ∽△AND .(2)由△AMB ∽△AND 得AM AN =ABAD ,∠BAM =∠DAN .又AD =BC ,∴AM AN =ABBC.∵AM ⊥BC ,AD ∥BC ,∴∠AMB =∠MAD =90°.∴∠B +∠BAM =∠MAN +∠NAD =90°, ∴∠B =∠MAN .∴△AMN ∽△BAC ,∴AM AB =MNAC. 题型6 等积代换法1.如图,在△ABC 中,AD ⊥BC 于D ,DE ⊥AB 于E ,DF ⊥AC 于F .求证:AE AF =ACAB .1.证明:∵AD ⊥BC ,DE ⊥AB ,∴∠ADB =∠AED =90°. 又∵∠BAD =∠DAE ,∴△ADE ∽△ABD ,得AD 2=AE ·AB ,同理可得AD 2=AF ·AC ,∴AE ·AB =AF ·AC ,∴AE AF =AC AB.题型7 等线段代换法1.如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于点D ,点P 是AD 上一点,CF ∥AB ,延长BP 交AC 于点E ,交CF 于点F ,求证:BP 2=PE ·PF .1.证明:连接PC ,如图.∵AB =AC ,AD ⊥BC ,∴AD 垂直平分BC ,∠ABC =∠ACB ,∴BP =CP ,∴∠1=∠2,∴∠ABC -∠1=∠ACB -∠2,即∠3=∠4.∵CF ∥AB ,∴∠3=∠F ,∴∠4=∠F .又∵∠CPF =∠CPE ,∴△CPF ∽△EPC ,∴CP PE =PFCP ,即CP 2=PF ·PE .∵BP=CP ,∴BP 2=PE ·PF .2.已知:如图,AD 平分∠BAC ,AD 的垂直平分线EP 交BC 的延长线于点P .求证:PD 2=PB ·PC .2.证明:如图,连接PA ,则PA =PD ,∴∠PDA =∠PAD . ∴∠B +∠BAD =∠DAC +∠CAP .又∵AD 平分∠BAC ,∴∠BAD =∠DAC .∴∠B =∠CAP . 又∵∠APC =∠BPA ,∴△PAC ∽△PBA ,∴PA PB =PCPA ,即PA 2=PB ·PC ,∴PD 2=PB ·PC .类型2 巧用“基本图形”探索相似条件方法指导:几何图形大多数由基本图形复合而成,因此熟悉三角形相似的基本图形,有助于快速、准确地识别相似三角形,从而顺利找到解题思路和方法.相似三角形的四类结构图:1.平行线型.2.相交线型.3.母子型型.4.旋转型.1.如图,在△ABC 中,BE 平分∠ABC 交AC 于点E ,过点E 作ED ∥BC 交AB 于点D .(1)求证:AE ·BC =BD ·AC ;(2)如果S △ADE =3,S △BDE =2,DE =6,求BC 的长.1.(1)证明:∵ED ∥BC ,∴△ADE ∽△ABC .∴AE AC =DEBC .∵BE 平分∠ABC ,∴∠DBE =∠EBC . ∵ED ∥BC ,∴∠DEB =∠EBC . ∴∠DBE =∠DEB .∴DE =BD .∴AE AC =BD BC, 即AE ·BC =BD ·AC .(2)解:设h △ADE 表示△ADE 中DE 边上的高, h △BDE 表示△BDE 中DE 边上的高, h △ABC 表示△ABC 中BC 边上的高.∵S △ADE =3,S △BDE =2,∴S △ADE S △BDE =h △ADE h △BDE =32.∴h △ADE h △ABC =35.∵△ADE ∽△ABC ,∴DE BC =h △ADE h △ABC =35. ∵DE =6,∴BC =10.题型2 相交线型1.如图,点D ,E 分别为△ABC 的边AC ,AB 上的点,BD ,CE 交于点O ,且EO BO =DOCO ,试问△ADE 与△ABC 相似吗?请说明理由.2.解:相似.理由如下:因为EO BO =DO CO,∠BOE =∠COD ,∠DOE =∠COB ,所以△BOE ∽△COD ,△DOE ∽△COB .所以∠EBO =∠DCO ,∠DEO =∠CBO .因为∠ADE =∠DCO +∠DEO ,∠ABC =∠EBO +∠CBO .所以∠ADE =∠ABC .又因为∠A =∠A ,所以△ADE ∽△ABC .1.如图,在△ABC 中,∠BAC =90°,AD ⊥BC 于点D ,E 为AC 的中点,ED 的延长线交AB 的延长线于点F .求证:AB AC =DFAF .1.证明:∵∠BAC =90°,AD ⊥BC 于点D , ∴∠BAC =∠ADB =90°.又∵∠CBA =∠ABD (公共角),∴△ABC ∽△DBA .∴AB AC =DBDA ,∠BAD =∠C .∵AD ⊥BC 于点D ,E 为AC 的中点,∴DE =EC . ∴∠BDF =∠CDE =∠C .∴∠BDF =∠BAD . 又∵∠F =∠F , ∴△DBF ∽△ADF .∴DB AD =DF AF .∴AB AC =DF AF.点拨:当所证等积式或比例式运用“三点定型法”不能定型或能定型而不相似,条件又不具备成比例线段时,可考虑用中间比“搭桥”,称为“等比替换法”,有时还可用“等积替换法”,例如:如图,在△ABC 中,AD ⊥BC 于点D ,DE ⊥AB 于点E ,DF ⊥AC 于点F ,求证:AE ·AB =AF ·AC .可由两组“射影图”得AE ·AB =AD 2,AF ·AC =AD 2,∴AE ·AB =AF ·AC .题型4 旋转型4.如图,已知∠DAB =∠EAC ,∠ADE =∠ABC . 求证:(1)△ADE ∽△ABC ; (2)AD AE =BD CE .4.证明:(1)∵∠DAB =∠EAC ,∴∠DAE =∠BAC . 又∵∠ADE =∠ABC ,∴△ADE ∽△ABC . (2)∵△ADE ∽△ABC ,∴AD AE =ABAC.∵∠DAB =∠EAC ,∴△ADB ∽△AEC .∴AD AE =BDCE.类型3 利用相似三角形巧证线段的数量和位置关系方法指导:判断两线段之间的数量和位置关系是几何中的基本题型之一.由角的关系推出“平行或垂直”是判断位置关系的常用方法,由相似三角形推出“相等”是判断数量关系的常用方法.题型1 证明两线段的数量关系 类型1:证明两线段的相等关系1.如图,已知在△ABC 中,DE ∥BC ,BE 与CD 交于点O ,直线AO 与BC 边交于点M ,与DE 交于点N .求证:BM =MC .1.证明:∵DE ∥BC .∴△NEO ∽△MBO .∴NE MB =ON OM. 同理可得DN MC =ON OM .∴DN MC =NE BM .∴DN NE =MCBM .∵DE ∥BC ,∴△ANE ∽△AMC .∴AN AM =NEMC .同理可得AN AM =DN BM ,∴DN BM =NE MC .∴DN NE =BMMC .∴MC BM =BM MC.∴MC 2=BM 2.∴BM =MC .2.如图,一直线和△ABC 的边AB ,AC 分别交于点D ,E ,和BC 的延长线交于点F ,且AE CE =BF CF .求证:AD =DB .2.证明:如图,过C 作CG ∥AB 交DF 于G 点. ∵CG ∥AB ,∴AD CG =AE CE ,BD CG =BFCF,∵AE CE =BF CF ,∴AD CG =BD CG, ∴AD =BD .类型2:证明两线段的倍分关系1.如图,在△ABC 中,BD ⊥AC 于点D ,CE ⊥AB 于点E ,∠A =60°,求证:DE =12BC .2.证明:∵BD ⊥AC ,CE ⊥AB ,∠A =60°,∠ABD =∠ACE =30°,∴AD AB =12,AEAC =12,∴AD AB =AE AC .又∠A =∠A ,∴△AD E ∽△ABC ,∴DE BC =AD AB =12,∴DE =12BC.4.如图,AM 为△ABC 的角平分线,D 为AB 的中点,CE ∥AB ,CE 交DM 的延长线于E .求证:AC =2CE .4.证明:如图,延长CE ,交AM 的延长线于F .∵AB ∥CF ,∴∠BAM =∠F ,△BDM ∽△CEM ,△BAM ∽△CFM ,∴BD CE =BM MC ,BA CF =BM MC ,∴BD CE =BA CF.又∵BA =2BD ,∴CF =2CE .又AM 平分∠BAC ,∴∠BAM =∠CAM ,∴∠CAM =∠F ,∴AC =CF ,∴AC =2CE .题型2 证明两线段的位置关系 类型1:证明两线段平行1.如图,已知点D 为等腰直角三角形ABC 的斜边AB 上一点,连接CD ,DE ⊥CD ,DE =CD ,连接CE ,AE .求证:AE ∥BC .1.证明:如图,过点C 作CO ⊥AB 于点O .∵DE =CD ,DE ⊥CD , ∴∠ECD =∠CED =45°.∵△ABC 是等腰直角三角形,∴∠CAB =∠B =45°.∴∠CAB =∠CED .又∵∠AOC =∠EDC =90°,∴△ACO ∽△ECD .∴AC CO =EC CD .又∵∠ACE +∠ECO =∠OCD +∠ECO =45°,∴∠ACE=∠OCD .∴△ACE ∽△OCD .∴∠CAE =∠COD =90°.又∵∠ACB =90°,∴∠CAE +∠ACB =180°.∴AE ∥BC .2.在△ABC 中,D ,E ,F 分别为BC ,AB ,AC 上的点,EF ∥BC ,DF ∥AB ,连接CE 和AD ,分别交DF ,EF 于点N ,M .(1)如图①,若E 为AB 的中点,图中与MN 平行的直线有哪几条?请证明你的结论;(2)如图②,若E 不为AB 的中点,写出与MN 平行的直线,并证明.2.解:(1)MN ∥AC ∥ED .证明如下:∵EF ∥BC ,∴△AEM ∽△ABD ,△AMF ∽△ADC ,∴EM BD =AM AD =MF DC .∵E 为AB 的中点,EF ∥BC ,∴F 为AC 的中点.又∵DF ∥AB ,∴D 为BC 的中点,∴EM =MF .∵F 为AC 的中点,FN ∥AE ,∴N 为EC 的中点,从而MN ∥AC .又∵D 为BC 的中点,E 为AB 的中点,∴ED ∥AC ,∴MN ∥AC ∥ED .(2)MN ∥AC .证明如下:∵EF ∥BC ,∴△AEM ∽△ABD ,△AMF ∽△ADC ,∴EM BD =AMAD =MF DC ,∴EM MF =BD DC .又∵DF ∥AB ,∴BD DC =EN NC ,∴EM MF =EN NC ,∴EM EF =EN EC.又∵∠MEN =∠FEC ,∴△MEN ∽△FEC .∴∠EMN =∠EFC .∴MN ∥AC .类型2:证明两线垂直1.如图,在△ABC 中,D 是AB 上一点,且AC 2=AB ·AD ,BC 2=BA ·BD ,求证:CD ⊥AB .1.证明:∵AC 2=AB ·AD ,∴AC AD =ABAC .又∵∠A =∠A ,∴△ACD ∽△ABC .∴∠ADC =∠ACB .又∵BC 2=BA ·BD ,∴BC BD =BABC .又∵∠B =∠B ,∴△BCD ∽△BAC .∴∠BDC =∠BCA . ∴∠ADC =∠BDC .∵∠BDC +∠ADC =180°,∴∠ADC =∠BDC =90°. ∴CD ⊥AB .2.如图,已知矩形ABCD ,AD =13AB ,点E ,F 把AB 三等分,DF 交AC 于点G ,求证:EG ⊥DF .2.证明:∵AD =13AB ,点E ,F 把AB 三等分,∴设AE =EF =FB =AD =k ,则AB =CD =3k .∵CD ∥AB ,∴∠DCG =∠FAG ,∠CDG =∠AFG . ∴△AFG ∽△CDG ,∴FG DG =AF CD =23.设FG =2m ,则DG =3m ,∴DF =FG +DG =2m +3m =5m . 在Rt △AFD 中,DF 2=AD 2+AF 2=5k 2,∴DF =5k . ∴5m =5k .∴m =55k .∴FG =255k . ∴AF FG =2k 255k =5,DF EF =5k k = 5.∴AF FG =DFEF. 又∠AFD =∠GFE ,∴△AFD ∽△GFE . ∴∠EGF =∠DAF =90°.∴EG ⊥DF .类型4 相似三角形与函数的综合应用方法指导:解涉及相似三角形与函数的综合题时,由于这类题的综合性强,是中考压轴题重点命题形式之一,因此解题时常结合方程思想、分类讨论思想进行解答.题型1 相似三角形与一次函数1.如图,在平面直角坐标系xOy 中,直线y =-x +3与x 轴交于点C ,与直线AD 交于点A ⎝ ⎛⎭⎪⎫43,53,点D 的坐标为(0,1).(1)求直线AD 的解析式;(2)直线AD 与x 轴交于点B ,若点E 是直线AD 上一动点(不与点B 重合),当△BOD 与△BCE 相似时,求点E 的坐标.1.解:(1)设直线AD 的解析式为y =kx +b (k ≠0) 将D (0,1) A ⎝⎛⎭⎫43,53代入解析式得: ⎩⎪⎨⎪⎧b =153=43k +b 解得⎩⎪⎨⎪⎧b =1k =12∴直线AD 的解析式为y =12x +1.(2)直线AD 的解析式为y =12x +1.令y =0,得x =-2.得B (-2,0),即OB =2. 直线AC 为y =-x +3. 令y =0,得∴x =3. 得C (3,0),即BC =5 设E ⎝⎛⎭⎫x ,12x +1 ①当E 1C ⊥BC 时,如图,∠BOD =∠BCE 1=90°,∠DBO =∠E 1BC .∴△BOD ∽△BCE 1. 此时点C 和点E 1的横坐标相同. 将x =3代入y =12x +1,解得y =52.∴E 1⎝⎛⎭⎫3,52. ②当CE 2⊥AD 时,如图, ∠BOD =∠BE 2C =90°,∠DBO =∠CBE 2, ∴△BOD ∽△BE 2C .过点E 2作EF ⊥x 轴于点F ,则∠E 2FC =∠BFE 2=90°. 又∵∠E 2BF +∠BE 2F =90°, ∠CE 2F +∠BE 2F =90°.∴∠E 2BF =∠CE 2F .∴△E 2BF ∽△CE 2F ,则E 2F BF =CFE 2F .即E 2F 2=CF ·BF .⎝⎛⎭⎫12x +12=(3-x )(x +2)解得:x 1=2,x 2=-2(舍去)∴E 2(2,2) 当∠EBC =90°时,此情况不存在. 综上所述:E 1⎝⎛⎭⎫3,52或E 2(2,2).题型2 相似三角形与二次函数1.如图,直线y =-x +3交x 轴于点A ,交y 轴于点B ,抛物线y =ax 2+bx +c 经过A ,B ,C (1,0)三点.(1)求抛物线对应的函数解析式;(2)若点D 的坐标为(-1,0),在直线y =-x +3上有一点P ,使△ABO 与△ADP 相似,求出点P 的坐标.2.解:(1)由题意得A (3,0),B (0,3),∵抛物线经过A ,B ,C 三点,∴把A (3,0),B (0,3),C (1,0)三点的坐标分别代入y =ax 2+bx +c ,得方程组⎩⎪⎨⎪⎧9a +3b +c =0,c =3,a +b +c =0,解得⎩⎪⎨⎪⎧a =1,b =-4,c =3,∴抛物线对应的函数解析式为y =x 2-4x +3.(2)如图,由题意可得△ABO 为等腰直角三角形.若△ABO ∽△AP 1D ,则AO AD =OBDP 1,∴DP 1=AD =4,∴P 1(-1,4);若△ABO ∽△ADP 2,过点P 2作P 2M ⊥x 轴于M ,∵△ABO 为等腰直角三角形,∴△ADP 2是等腰直角三角形,由三线合一可得DM =AM =2=P 2M ,即点M 与点C 重合,∴P 2(1,2),∴点P 的坐标为(-1,4)或(1,2).2.如图,直线y =2x +2与x 轴交于点A ,与y 轴交于点B ,把△AOB 沿y 轴翻折,点A 落到点C ,过点B 的抛物线y =-x 2+bx +c 与直线BC 交于点D (3,-4).(1)求直线BD 和抛物线对应的函数解析式;(2)在第一象限内的抛物线上,是否存在一点M ,作MN 垂直于x 轴,垂足为点N ,使得以M ,O ,N 为顶点的三角形与△BOC 相似?若存在,求出点M 的坐标;若不存在,请说明理由.2.解:(1)易得A (-1,0),B (0,2),C (1,0). 设直线BD 对应的函数解析式为y =kx +m .把B (0,2),C (1,0)的坐标分别代入y =kx +m ,得⎩⎪⎨⎪⎧m =2,k +m =0,解得⎩⎪⎨⎪⎧k =-2,m =2.∴直线BD 对应的函数解析式为y =-2x +2. ∵抛物线对应的函数解析式为y =-x 2+bx +c .∴把B (0,2),D (3,-4)的坐标分别代入y =-x 2+bx +c ,得⎩⎪⎨⎪⎧c =2,-9+3b +c =-4,解得⎩⎪⎨⎪⎧b =1,c =2. ∴抛物线对应的函数解析式为y =-x 2+x +2.(2)存在,①如图①,当△MON ∽△BCO 时,ON CO =MN BO ,即ON 1=MN 2,∴MN =2ON .设ON =a ,则M (a ,2a ),∴-a 2+a +2=2a ,解得a 1=-2(不合题意,舍去),a 2=1,∴M (1,2);②如图②,当△MON ∽△CBO 时,ON BO =MN CO ,即ON 2=MN 1,∴MN =12ON .设ON =n ,则M ⎝⎛⎭⎫n ,12n ,∴-n 2+n +2=n2,解得n 1=1-334(不合题意,舍去),n 2=1+334,∴M (1+334,1+338).∴存在这样的点M (1,2)或⎝ ⎛⎭⎪⎫1+334,1+338.题型3 相似三角形与反比例函数1.如图,矩形OABC 的顶点A ,C 分别在x 轴和y 轴上,点B 的坐标为(2,3),双曲线y =kx (x >0)经过BC 的中点D ,且与AB 交于点E ,连接DE .(1)求k 的值及点E 的坐标;(2)若点F 是OC 边上一点,且△FBC ∽△DEB ,求直线FB 对应的函数解析式.1.解:(1)在矩形OABC 中,∵点B 的坐标为(2,3),∴BC 边的中点D 的坐标为(1,3).∵双曲线y =k x 经过点D (1,3),∴3=k 1,∴k =3,∴y =3x .∵点E 在AB 上,∴点E 的横坐标为2.又∵双曲线y =3x 经过点E ,∴点E 的纵坐标为y =32,∴点E 的坐标为⎝⎛⎭⎫2,32. (2)易得BD =1,BE =32,CB =2.∵△FBC ∽△DEB ,∴BD CF =BE CB ,即1CF =322,∴CF =43,∴OF =53,即点F 的坐标为⎝⎛⎭⎫0,53.设直线FB 对应的函数解析式为y =k 1x +b ,而直线FB 经过B (2,3),F ⎝⎛⎭⎫0,53,∴k 1=23,b =53,∴直线FB 对应的函数解析式为y =23x +53.类型5 全章达标综合检测方法指导:本章主要内容为:平行线分线段成比例,相似三角形的判定及性质,位似图形及其画法等,涉及考点、考法较多,是中考的高频考点.其主要考点可概括为:3个概念、2个性质、1个判定、2个应用、1个作图、1个技巧.题型1 3个概念 概念1:成比例线段1.下列各组线段,是成比例线段的是( C ) A .3 cm ,6 cm ,7 cm ,9 cm B .2 cm ,5 cm ,0.6 dm ,8 cm C .3 cm ,9 cm ,1.8 dm ,6 cm D .1 cm ,2 cm ,3 cm ,4 cm2.有一块三角形的草地,它的一条边长为25 m ,在图纸上,这条边的长为5 cm ,其他两条边的长都为4 cm ,则其他两边的实际长度都是__20__m .概念2:相似多边形3.如图,已知∠1′=∠1,∠2′=∠2,∠3′=∠3,∠4′=∠4,∠D ′=∠D ,试判断四边形A ′B ′C ′D ′与四边形ABCD 是否相似,并说明理由.3.解:四边形ABCD 与四边形A ′B ′C ′D ′相似.由已知条件知,∠DAB =∠D ′A ′B ′,∠B =∠B ′,∠BCD =∠B ′C ′D ′,∠D =∠D ′,且AB A′B′=BC B′C′=CD C′D′=DA D′A′=56,所以四边形ABCD 与四边形A ′B ′C ′D ′相似.概念3:位似图形4.如图,在△ABC 中,A ,B 两个顶点在x 轴的上方,点C 的坐标是(-1,0).以点C 为位似中心,在x 轴的下方作△ABC 的位似图形,并把△ABC 的边放大到原来的2倍,记所得的像是△A ′B ′C .设点B 的对应点B ′的坐标是(a ,b ),求点B 的坐标.4.解:如图,过点B 作BM ⊥x 轴于点M ,过点B ′作B ′N ⊥x 轴于点N ,则△CBM ∽△CB ′N .所以MC NC =BM B ′N =BC B ′C .又由已知条件知NC =a +1,B ′N =-b ,BC B ′C =,所以MCa +1)=BM-b )=所以MC =12(a +1),BM =-b 2.所以MO =12(a +1)+1=a +32.所以点B 的坐标为⎝⎛⎭⎫-a +32,-b2.题型2 2个性质平行线分线段成比例的性质5.如图,在Rt △ABC 中,∠A =90°,AB =8,AC =6.若动点D 从点B 出发,沿线段BA 运动到点A 为止,运动速度为每秒2个单位长度.过点D 作DE ∥BC 交AC 于点E ,设动点D 运动的时间为x 秒,AE 的长为y .(1)求出y 关于x 的函数解析式,并写出自变量x 的取值范围; (2)当x 为何值时,△BDE 的面积有最大值,最大值为多少?5.解:(1)∵DE ∥BC ,∴AD AB =AE AC ,∴8-2x 8=y 6,∴y =-32x +6(0≤x ≤4).(2)∵S △BDE =12·2x ·y =12·2x ·⎝⎛⎭⎫6-32x =-32(x -2)2+6,∴当x =2时,S △BDE 有最大值,最大值为6.性质2:相似三角形的性质6.如图,已知D 是BC 边上的中点,且AD =AC ,DE ⊥BC ,DE 与BA 相交于点E ,EC 与AD 相交于点F .(1)求证:△ABC ∽△FCD ;(2)若S △FCD =5,BC =10,求DE 的长.6.(1)证明:如图,∵D 是BC 边上的中点,DE ⊥BC , ∴EB =EC ,∴∠B =∠1.又∵AD =AC ,∴∠ACD =∠2,∴△ABC ∽△FCD . (2)解:如图,过点A 作AM ⊥CB 于点M . ∵D 是BC 边上的中点,∴BC =2CD .由(1)知△ABC ∽△FCD ,∴S △ABC S △FCD =⎝ ⎛⎭⎪⎫BC CD 2=41.又∵S △FCD =5,∴S △ABC =20.∵S △ABC =12BC ·AM ,∴AM =2S △ABC BC =2×2010=4. ∵DE ⊥BC ,AM ⊥BC ,∴DE ∥AM ,∴△BDE ∽△BMA .∴DE AM =BDBM .由AD =AC ,AM ⊥BC ,知DM =12CD =14BC =52. ∴DE 4=55+52,∴DE =83. 点拨:从复杂的图形中分析线段的特点和联系,找到切入点是解较复杂问题的关键.题型3 1个判定——相似三角形的判定7.如图,△ACB 为等腰直角三角形,点D 为斜边AB 上一点,连接CD ,DE ⊥CD ,DE =CD ,连接AE ,过C 作CO ⊥AB 于O .求证:△ACE ∽△OCD.7.证明:∵△ACB 为等腰直角三角形,AB 为斜边, ∴∠CAB =45°.∵CO ⊥AB .∴∠AOC =90°.又∵DE ⊥CD ,DE =CD ,∴∠CED =45°,∠CDE =90°. ∴∠CAO =∠CED ,∠AOC =∠EDC .∴△ACO ∽△ECD .∴∠ACO =∠ECD ,AC CO =CECD .∴∠ACE =∠OCD .∴△ACE ∽△OCD .8.如图,在⊙O 的内接△ABC 中,∠ACB =90°,AC =2BC ,过点C 作AB 的垂线l 交⊙O 于另一点D ,垂足为点E .设P 是AC ︵上异于点A ,C 的一个动点,射线AP 交l 于点F ,连接PC 与PD ,PD 交AB 于点G .(1)求证:△PAC ∽△PDF ;(2)若AB =5,AP ︵=BP ︵,求PD 的长.8.(1)证明:由四边形APCB 内接于圆O ,得∠FPC =∠B . 又∠B =∠ACE =90°-∠BCE ,∠ACE =∠APD ,所以∠APD =∠FPC ,所以∠APD +∠DPC =∠FPC +∠DPC , 即∠APC =∠FPD . 又∠PAC =∠PDC , 所以△PAC ∽△PDF .(2)解:由(1)知△PAC ∽△PDF ,所以∠PCA =∠PFD . 又∠PAC =∠CAF ,所以△PAC ∽△CAF ,所以△CAF ∽△PDF , 所以PD AC =DFAF,则PD ·AF =AC ·DF .由AB =5,AC =2BC ,∠ACB =90°,知BC =5,AC =2 5. 由OE ⊥CD ,∠ACB =90°知CB 2=BE ·AB ,CE =DE . 所以B E =CB 2AB =55=1.所以AE =4,CE =CB 2-BE 2=5-1=2, 所以DE =2.又AP ︵=BP ︵,∠AFD =∠PCA ,所以∠AFD =∠PCA =45°. 所以FE =AE =4,AF =42,所以PD =AC·DF AF =25×(4+2)42=3102.题型4 2个应用 应用1:测高的应用9.如图,在离某建筑物CE 4 m 处有一棵树AB ,在某时刻,1.2 m 的竹竿FG 垂直地面放置,影子GH 长为2 m ,此时树的影子有一部分落在地面上,还有一部分落在建筑物的墙上,墙上的影子CD 高为2 m ,那么这棵树的高度是多少?9.解:(方法一:作延长线)延长AD ,与地面交于点M ,如图①.由AM ∥FH 知∠AMB =∠FHG .又因为AB ⊥BG ,FG ⊥BG ,DC ⊥BG ,所以△ABM ∽△DCM ∽△FGH ,所以AB BM =CD CM =FG GH. 因为CD =2 m ,FG =1.2 m ,GH =2 m ,所以2CM =1.22,解得CM =103m . 因为BC =4 m ,所以BM =BC +CM =4+103=223(m ). 所以AB 223=1.22,解得AB =4.4 m . 故这棵树的高度是4.4 m .(方法二:作垂线)过点D 作DM ⊥AB 于点M ,如图②.所以AM DM =FG GH. 而DM =BC =4 m ,AM =AB -CD =AB -2(m ),FG =1.2 m ,GH =2 m ,所以AB -24=1.22,解得AB =4.4 m . 故这棵树的高度是4.4 m .应用2:测宽的应用10.如图,一条小河的两岸有一段是平行的,在河的一岸每隔6 m 有一棵树,在河的对岸每隔60 m 有一根电线杆,在有树的一岸离岸边30 m 处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河的宽度.10.解:如图,过点A 作AF ⊥DE ,垂足为F ,并延长交BC 于点G .∵DE ∥BC ,∴△ADE ∽△ABC .∵AF ⊥DE ,DE ∥BC ,∴AG ⊥BC ,∴AF AG =DE BC ,∴30AG =2460. 解得AG =75,∴FG =AG -AF =75-30=45,即河的宽度为45 m .题型5 1个作图——作一个图形的位似图形11.如图,在方格纸中(每个小方格的边长都是1个单位长度)有一点O 和△ABC .请以点O 为位似中心,把△ABC 缩小为原来的一半(不改变方向),画出△ABC 的位似图形.(第11题) 11.思路导引:本题位似中心为O ,先连接CO ,因为要把原三角形缩小为原来的一半,可确定C ′O =12CO ,由其确定出C ′的位置,再根据同样的方法确定出另外两个点. 解:画出图形,如图中的△A ′B ′C ′即为所求作的图形.点拨:抓住位似图形的性质,根据位似中心与三角形对应点的关系及位似比的大小确定所画位似图形的对应点,再画出图形.题型6 1个技巧 ——证明四条线段成比例的技巧12.如图,已知△ABC ,∠BAC 的平分线与∠DAC 的平分线分别交BC 及BC 的延长线于点P ,Q .(1)求∠PAQ 的度数;(2)若点M 为PQ 的中点,求证:PM 2=CM ·BM .12.思路导引:(1)由角平分线的定义及∠BAD 为平角直接可得.(2)由于线段PM ,CM ,BM 在同一条直线上,所以必须把某条线段转化为另一相等的线段,构造相似三角形,因此可证PM =AM ,从而证明△ACM 与△ABM 相似即可.(1)解:∵AP 平分∠BAC ,∴∠PAC =12∠BAC . 又∵AQ 平分∠CAD ,∴∠CAQ =12∠CAD . ∴∠PAC +∠CAQ =12∠BAC +12∠CAD =12(∠BAC +∠CAD ). 又∵∠BAC +∠CAD =180°,∴∠PAC +∠CAQ =90°,即∠PAQ =90°.(2)证明:由(1)知∠PAQ =90°,又∵M 是线段PQ 的中点,∴PM =AM ,∴∠APM =∠PAM .∵∠APM =∠B +∠BAP ,∠PAM =∠CAM +∠PAC ,∠BAP =∠PAC ,∴∠B =∠CAM .又∵∠AMC =∠BMA ,∴△ACM ∽△BAM .∴CM AM =AM BM,∴AM 2=CM ·BM ,即PM 2=CM ·BM . 点拨:本题运用了转化思想,在证明等积式时,常把它转化成比例式,寻找相似三角形进行求解.。
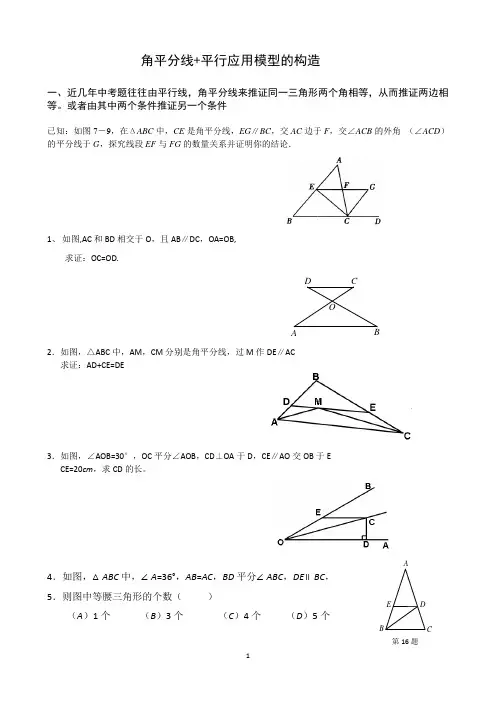
角平分线+平行应用模型的构造一、近几年中考题往往由平行线,角平分线来推证同一三角形两个角相等,从而推证两边相等。
或者由其中两个条件推证另一个条件已知:如图7-9,在ΔABC中,CE是角平分线,EG∥BC,交AC边于F,交∠ACB的外角(∠ACD)的平分线于G,探究线段EF与FG的数量关系并证明你的结论.1、如图,AC和BD相交于O,且AB∥DC,OA=OB,求证:OC=OD.OD CBA2.如图,△ABC中,AM,CM分别是角平分线,过M作DE∥AC求证:AD+CE=DE3.如图,∠AOB=30°,OC平分∠AOB,CD⊥OA于D,CE∥AO交OB于ECE=20cm,求CD的长。
4.如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,5.则图中等腰三角形的个数()(A)1个(B)3个(C)4个(D)5个AEB CD第16题EFCBAD5如右图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF 等于( )A.5 B.4 C . 3 D .26、如图,四边形ABCD 中,AD∥BC ,∠ABD =30o,AB=AD ,DC ⊥BC 于点C ,若BD =2,求CD 的长。
二 由平行线想到全等三角形和等腰三角形。
例. 如图,已知,EG ∥AF ,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。
并证明这个命题(只写出一种情况)①AB=AC ②DE=DF ③BE=CF已知:EG ∥AF,_______,_________. 求证:___________. 证明:GFEDCBA1、已知:如图,△ABC 中,AB=AC ,D 点在AB 上,E 点在AC 的延长线上,且BD=CE ,连接DE ,交BC 于F.求证:DF=EF.C第6题FECDBA三、当题目中有角平分线时,可通过构造等腰三角形或全等三角形来寻找解题思路,或利用角平分线性质去证线段相等要证明两条线段的和与一条线段相等时常用的两种方法:(1)、可在长线段上截取与两条线段中一条相等的一段,然后证明剩余的线段与另一条线段相等。

专题27.43《相似》全章复习与巩固(知识讲解)【学习目标】1、了解比例的基本性质,线段的比、成比例线段;2、通过具体实例认识图形的相似,探索相似图形的性质,理解相似多边形对应角相等、对应边成比例、周长的比等于相似比、面积的比等于相似比的平方,探索并掌握相似三角形的判定方法,并能利用这些性质和判定方法解决生活中的一些实际问题;3、了解图形的位似,能够利用位似将一个图形放大或缩小,在同一直角坐标系中,感受位似变换后点的坐标的变化;4、结合相似图形性质和判定方法的探索和证明,进一步培养推理能力,发展逻辑思维能力和推理论证的表达能力,以及综合运用知识的能力,运用学过的知识解决问题的能力.【要点梳理】【知识点一】成比例线段1、定义:四条线段,,,a b c d 中,如果a 与b 的比等于c 与d 的比,即a cb d=,那么这四条线段,,,a b c d 叫做成比例线段,简称比例线段。
2、性质:(1)基本性质:如果a cb d=,那么ad bc =;反之,若ad bc =(),,,0a b c d 都不等于,那么a c b d =(2)等比性质:如果()==0a c m b d n b d n =+++≠ ,那么a c m a b d n b +++=+++ (3)合比性质:如果a c b d =,那么a b c d b d ++=,a b c d b d --=【知识点二】平行线分线段成比例1、定理:两条直线被一组平行线所截,所得的对应线段成比例2、推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例【知识点三】相似多边形1、定义:各角分别相等,各边成比例的两个多边形叫做相似多边形。
相似多边形对应边的比叫做相似比2、性质:相似多边形的周长比等于相似比,面积比等于相似比的平方【知识点四】相似三角形1、定义:三角分别相等,三边成比例的两个三角形叫做相似三角形2、判定:(1)两角分别相等的两个三角形相似(2)两边成比例且夹角相等的两个三角形相似(3)三边成比例的两个三角形相似3、性质:(1)相似三角形的对应角相等,对应边成比例(2)相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比(3)相似三角形的周长比等于相似比,面积比等于相似比的平方【知识点五】黄金分割点C 把线段AB 分成两条线段AC 和BC ()AC BC >,如果AC BC AB AC=,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比,即:0.618:1AC AB ≈【知识点六】位似图形1、定义:一般的,如果两个相似多边形任意一组对应顶点P ,'P 所在的直线都经过同一点O ,且有'OP =()0k OP k ⋅≠,那么这样的两个多边形叫做位似多边形,点O 叫做位似中心2、性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比3、画图步骤:(1)尺规作图法:①确定位似中心;②确定原图形中的关键点关于中心的对应点;③描出新图形(2)坐标法:在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘于同一个数()0k k ≠,所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比为k【典型例题】类型一、成比例线段和平行线分线段成比例1.已知三条线段a b c ,,满足1324a b c +==,且17a b c ++=.(1)求a b c ,,的值;(2)若线段d 是线段a 和b 的比例中项,求d 的值.【点拨】本题考查了比例的性质,比例线段,利用“设k 法”用k 表示出a 、b 、c 可以使计算更加简便.【变式1】已知:2:3,:3:4a b b c ==,且26a b c +-=,求,,a b c 的值【答案】4a =,6b =,8c =.【分析】根据比的性质,可得a ,b ,c 用k 表示,根据解方程,可得k 的值,即可得答案.解:∵:2:3a b =,:3:4b c =,∴设2a k =,3b k =,4c k =,∴()22346k k k ⋅+-=,整理得:36k = ,解得:2k =,∴24a k ==,36b k ==,48c k ==.【点拨】本题考查了比例的性质,利用比例的性质得出2a k =,3b k =,4c k =是解题关键.【变式2】如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF PD=,以AF为边作正方形AMEF,点M在AD上.,的长;(1)求AM DM(2)点M是AD的黄金分割点吗?为什么?【点拨】此题综合考查了正方形的性质、勾股定理和黄金分割的概念.先求得线段AM,DM的长,然后求得线段AM和AD,DM和AM之间的比,根据黄金分割的概念进行判断.2.如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若25DE EF =,AC=14,(1)求AB 的长.(2)如果AD=7,CF=14,求BE 的长.【点拨】本题考查平行线分线段成比例的知识,解题的关键是掌握三条平行线截两条直线,所得的对应线段成比例.【变式1】如图,已知AD//BE//CF,它们依次交直线1l、2l于点A、B、C和点D、E、F,且AB=6,BC=8.(1)求DEDF的值;(2)当AD=5,CF=19时,求BE的长.【点拨】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;熟练掌握平行线分线段成比例,通过作辅助线运用平行线分线段成比例求出BH 是解决问题的关键.【变式2】如图,在ABC ∆中,点D 是边AB 上的一点.(1)请用尺规作图法,在ABC ∆内,求作ADE ∠,使ADE B ∠=∠,DE 交AC 于E ;(不要求写作法,保留作图痕迹)(2)在(1)的条件下,若2AD DB =,求AE EC的值.【点拨】本题考查了作一个角等于已知角,平行线分线段成比例定理,熟练掌握利用尺规作一个角等于已知角的作图方法是解题的关键.类型二、相似三角形判定和性质3.如图,在ABC 中,90ACB ∠=︒,CD 是边AB 上的中线,EF 垂直平分CD ,分别交AC ,BC 于E ,F ,连接DE ,DF .(1)求证:OCE OFD ∽△△.(2)当7AE =,24BF =时,求线段EF 的长.【答案】(1)见分析(2)25EF =【分析】(1)如图(见分析),先根据线段垂直平分线的性质可得90EOC DOF ∠=∠=︒,ED EC =,FD FC =,再根据三角形全等的判定定理证出EDF ECF ≅ ,根据全等三角形的性质可得12∠=∠,从而可得421∠=∠=∠,然后根据相似三角形的判定即可得证;(2)如图(见分析),延长FD 至G ,使DG DF =,连接AG ,EG ,先根据线段垂直平分线的判定与性质可得EG EF =,再根据三角形全等的判定定理证出ADG BDF ≅△△,根据全等三角形的性质可得24AG BF ==,7B ∠=∠,然后根据平行线的判定与性质可得90EAG ∠=︒,最后在Rt AEG △中,利用勾股定理即可得.(1)证明:∵EF 垂直平分CD ,∴90EOC DOF ∠=∠=︒,ED EC =,FD FC =,在EDF 和ECF △中,ED EC FD FC EF EF =⎧⎪=⎨⎪=⎩,∴()EDF ECF SSS ≅ ,∴12∠=∠,∵90ACB ∠=︒,90EOC ∠=︒,∴233490∠+∠=∠+∠=︒,∴421∠=∠=∠,在OCE △和OFD △中,9014EOC DOF ∠=∠=︒⎧⎨∠=∠⎩,∴OCE OFD .(2)解:如图,延长FD 至G ,使DG DF =,连接AG ,EG .则ED 垂直平分FG ,【点拨】本题考查了相似三角形的判定、三角形全等的判定定理与性质、线段垂直平分线的判定与性质等知识点,较难的是题(2),构造全等三角形和直角三角形是解题关键.【变式1】如图,四边形ABCD 中,AC 平分∠DAB ,∠ADC=∠ACB=90°,E 为AB 的中点,(1)求证:AC 2=AB•AD ;(2)求证:CE ∥AD ;(3)若AD=4,AB=6,求的值.=.∴AF4【变式2】如图,在△ABC中,(1)求作:∠BAD=∠C,AD交BC于D.(用尺规作图法,保留作图痕迹,不要求写作法).(2)在(1)条件下,求证:AB2=BD•BC.【点拨】本题考查了基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了相似三角形的判定与性质.中,过点C作CD//AB,E是AC的中点,连接DE并延长,4.如图,在ABC交AB于点F,交CB的延长线于点G,连接AD,CF()1求证:四边形AFCD是平行四边形.()2若GB3=,BC6=,3BF=,求AB的长.2【变式1】已知:如图6,菱形ABCD,对角线AC、BD交于点O,BE⊥DC,垂足为E,交AC于点F.求证:(1)△ABF∽△BED;(2)求证:AC BD BE DE=.【变式2】如图,已知▱ABCD.(1)用直尺和圆规在BC边上取一点E,使AB=AE,连结AE;(保留作图痕迹,不写作法)(2)在(1)的前提下,求证:AE=CD;∠EAD=∠D;(3)若点E为BC的中点,连接BD,交AE于F,直接写出EF:FA的值.【答案】(1)见分析(2)证明见分析(3)1:2分析:(1)以点A为圆心,AB为半径作圆,该圆与BC的交点即为所求的点E;(2)根据平行四边形的对边互相平行可得AD∥BC,再根据两直线平行,内错角相等可得∠AEB=∠EAD,根据等边对等角可得∠ABE=∠AEB,即可得证;(3)由四边形ABCD是平行四边形,可证得△BEF∽△AFD即可求得EF∶FA的值.解:(1)如图所示:;(2)证明:在平行四边形ABCD中,AD∥BC,∴∠AEB=∠EAD,∵AE=AB,∴∠ABE=∠AEB,∴∠B=∠EAD,∵∠B=∠D,∴∠DAE=∠D;(3)解:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴△BEF ∽△AFD ,∴=,∵E 为BC 的中点,∴BE=BC=AD ,∴EF :FA=1:2.【点拨】此题考查了相似三角形的判定与性质与平行四边形的性质,熟练掌握平行四边形的性质是关键.5.如图,在ABC 中,点D 、点E 分别在AC 、AB 上,点P 是BD 上的一点,联结EP 并延长交AC 于点F ,且A EPB ECB ∠=∠=∠.(1)求证:BE BA BP BD ⋅=⋅;(2)若90ACB ∠=︒,求证:CP BD ⊥.【变式1】已知ADE C ∠=∠,AG 平分BAC ∠交DE 于F ,交BC 于G .(1)求证:ADF ∽ACG ;(2)连接DG ,若DG AC ∥,25AF AG =,6AD =,求CE 的长度.【点拨】本题考查了相似三角形的判定和性质、角平分线的性质、平行线的性质、等腰三角形的判定和性质,解决本题的关键是掌握以上的定理并熟练的运用.【变式2】如图,∠A=∠C=∠EDF,CF=4,CD=AD=6;(1)求AE的长.(2)求证:△ADE∽△DFE.【点拨】此题考查了相似三角形的判定和性质,掌握相似三角形的判定方法以及根据相似三角形性质列出比例式进行求解是解题的关键.类型三、相似三角形拓展与提升6.已知△ABC中,∠ACB=90°,AC=BC=4cm,点P从点A出发,沿AB方向cm的速度向终点B运动,同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,设运动的时间为t秒.(1)如图①,若PQ⊥BC,求t的值;(2)如图②,将△PQC沿BC翻折至△P′QC,当t为何值时,四边形QPCP′为菱形?【点拨】此题是相似形综合题,主要考查的是菱形的性质、等腰直角三角形的性质,线段垂直平分线的性质,用方程的思想解决问题是解本题的关键.【变式1】已知,点E 、F 、G 、H 分别在正方形ABCD 的边AB 、BC 、CD 、AD 上.(1)如图1,当四边形EFGH 是正方形时,求证:AE AH AB +=;(2)如图2,已知AE AH =,CF CG =,当AE 、CF 的大小有_________关系时,四边形EFGH 是矩形;(3)如图3,AE DG =,EG 、FH 相交于点O ,:4:5OE OF =,已知正方形ABCD 的边长为16,FH 长为20,当OEH △的面积取最大值时,判断四边形EFGH 是怎样的四边形?证明你的结论.【答案】(1)见分析(2)AE CF =(3)平行四边形,证明见分析【分析】(1)利用平行四边形的性质证得BEF AHE ∠=∠,根据角角边证明AEH BFE △≌△.(2)当AE CF =,证得AEH FCG △≌△,EBF △是等腰直角三角形,∠HEF =∠EFG =90°,即可证得四边形EFGH 是矩形.(3)利用正方形的性质证得AEGD 为平行四边形,过点H 作HM BC ⊥,垂足为点M ,交EG 于点N ,由平行线分线段成比例,设4OE x =,5OF x =,HN h =,则可表示出HN ,从而把△OEH 的面积用x 的代数式表示出来,根据二次函数求出最大值,则可得OE =OG ,OF =OH ,即可证得平行四边形.解:(1)∵四边形ABCD 为正方形,∴90A B ∠=∠=︒,∴90AEH AHE ∠+∠=°.∵四边形EFGH 为正方形,∴EH EF =,90HEF ∠=︒,∴90AEH BEF ∠+∠=︒,∴BEF AHE ∠=∠.在AEH △和BFE △中,∵90A B ∠=∠=︒,AHE BEF ∠=∠,EH FE =,∴AEH BFE △≌△.∴AH BE =.∴AE AH AE BE AB +=+=;(2)AE CF =;证明如下:∵四边形ABCD 为正方形,∴90A B ∠=∠=︒,AB =BC =AD =CD ,∵AE =AH ,CF =CG ,AE =CF ,∴AH =CG ,∴AEH FCG △≌△,∴EH =FG .∵AE =CF ,∴AB -AE =BC -CF ,即BE =BF ,∴EBF △是等腰直角三角形,∴∠BEF =∠BFE =45°,∵AE =AH ,CF =CG ,∴∠AEH =∠CFG =45°,∴∠HEF =∠EFG =90°,∴EH ∥FG ,∴四边形EFGH 是矩形.(3)∵四边形ABCD 为正方形,∴AB CD ∥.【点拨】此题考查了正方形的性质,矩形的判定和平行四边形的性质与判定,平行线分线段成比例定理,全等三角形的判定与性质,等腰三角形的性质,二次函数的最值,有一定的综合性,解题的关键是熟悉这些知识并灵活运用.【变式2】已知点E在正方形ABCD的对角线AC上,正方形AFEG与正方形ABCD有公共点A.(1)如图1,当点G 在AD 上,F 在AB(2)将正方形AFEG 绕A 点逆时针方向旋转9(0)0αα︒<<︒,如图2,求:CE DG 的值为多少;(3)AB =AG AD =,将正方形AFEG 绕A 逆时针方向旋转(0360)αα︒<<︒,当C ,G ,E 三点共线时,请直接写出DG 的长度.正方形AFEG 绕A 点逆时针方向旋转DAG CAE∴∠=∠12AG AD AE AC == GAD EAC ∴ ∽ 82AB =,22AG =82AD AB ∴==,AG =,,G E C 三点共线,Rt AGC △中,GC AC =由(2)知△ADG∽△【点拨】本题考查了平行线分线段成比例,相似三角形的性质与判定,正方形的性质,勾股定理,旋转的性质,综合运用以上知识是解题的关键.类型三、位似7.如图,在6×8的网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.⑴以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2⑵连接⑴中的AA′,求四边形AA′C′C的周长.(结果保留根号)【点拨】此题主要考查了位似图形的画法以及勾股定理等知识,利用位似比得出对应点位置是解题关键.【变式一】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(5,2).(1)以点B为位似中心,在网格内画出△ABC的位似△A1BC1,使得△A1BC1与△ABC的位似比为2;(2)直接写出点A1的坐标和△A1BC1的面积.(2)如图所示1A :()3,7;11Δ116846222A BC S =⨯-⨯⨯-⨯【点拨】此题考查了位似变换和三角形面积求法,【变式二】如图,ABC 在平面直角坐标系内,三个顶点的坐标分别为()1,3A ,()2,1B ,()5,2C (正方形网格中,每个小正方形的边长为1),以点O 为位似中心,把ABC 按相似比2:1放大,得到对应A B C '''V .(1)请在第一象限内画出A B C '''V ;(2)若以点A 、B 、C 、D 为顶点的四边形是平行四边形,请直接写出满足条件的点D 的坐标.【答案】(1)见分析(2)()14,4D ;()26,0D ;()32,2D -【分析】(1)根据点O 为位似中心,()1,3A ,()2,1B ,()5,2C ,把ABC 按相似比2:1放大,得到对应A B C '''V ,求出点'A ,'B ,'C 的坐标,在网格中描点顺次连线即得;C(2)设D(x,y),∵平行四边形的对角线互相平分,且综上,()14,4D ;()26,0D ;()32,2D -.【点拨】本题主要考查了位似三角形,平行四边形,解决问题的关键是熟练掌握位似三角形的定义及画法,平行四边形对角线的性质和线段中点坐标公式.。
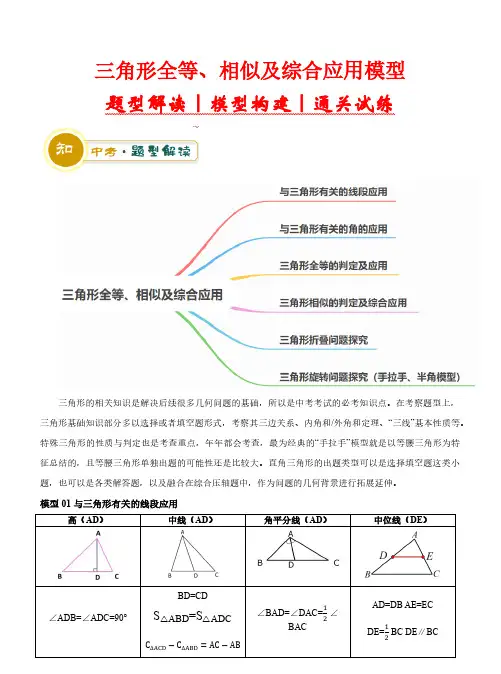
三角形全等、相似及综合应用模型题型解读|模型构建|通关试练三角形基础知识部分多以选择或者填空题形式,考察其三边关系、内角和/外角和定理、“三线”基本性质等。
特殊三角形的性质与判定也是考查重点,年年都会考查,最为经典的“手拉手”模型就是以等腰三角形为特征总结的,且等腰三角形单独出题的可能性还是比较大。
直角三角形的出题类型可以是选择填空题这类小题,也可以是各类解答题,以及融合在综合压轴题中,作为问题的几何背景进行拓展延伸。
模型01 与三角形有关的线段应用高(AD)中线(AD)角平分线(AD)中位线(DE)模型02 与三角形有关的角的应用(1)三角形的内角:(1)三角形内角的概念:三角形内角是三角形三边的夹角.每个三角形都有三个内角,且每个内角均大于0°且小于180°.(2)三角形内角和定理:三角形内角和是180°.(3)三角形内角和定理的证明证明方法,不唯一,但其思路都是设法将三角形的三个内角移到一起,组合成一个平角.在转化中借助平行线.(4)三角形内角和定理的应用主要用在求三角形中角的度数.①直接根据两已知角求第三个角;②依据三角形中角的关系,用代数方法求三个角;③在直角三角形中,已知一锐角可利用两锐角互余求另一锐角.(2)三角形的外角:(1)三角形外角的定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.三角形共有六个外角,其中有公共顶点的两个相等,因此共有三对.(2)三角形的外角性质:①三角形的外角和为360°.②三角形的一个外角等于和它不相邻的两个内角的和.③三角形的一个外角大于和它不相邻的任何一个内角.(3)若研究的角比较多,要设法利用三角形的外角性质②将它们转化到一个三角形中去.(4)探究角度之间的不等关系,多用外角的性质③,先从最大角开始,观察它是哪个三角形的外角.模型03 三角形全等的判定及应用(1)全等三角形的定义:全等的图形必须满足:(1)形状相同;(2)大小相等能够完全重合的两个三角形叫做全等三角形。

专题08三角形中的重要模型-平分平行(平分射影)构等腰、角平分线第二定理模型角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,,本专题就角平分线的非全等类模型作相应的总结,需学生反复掌握。
平分平行(射影)构等腰模型、角平行线第二定理模型(内角平分线定理和外角平分线定理模型)模型1、平分平行(射影)构等腰1)角平分线加平行线必出等腰三角形.模型分析:由平行线得到内错角相等,由角平分线得到相等的角,等量代换进行解题.平行线、角平分线及等腰,任意由其中两个条件都可以得出第三个。
(简称:“知二求一”,在以后还会遇到很多类似总结)。
平行四边形中的翻折问题就常出现该类模型。
图1图2图3条件:如图1,OO ’平分∠MON ,过OO ’的一点P 作PQ//ON.结论:△OPQ 是等腰三角形。
条件:如图2,△ABC 中,BD 是∠ABC 的角平分线,DE ∥BC 。
结论:△BDE 是等腰三角形。
条件:如图3,在ABC 中,BO 平分ABC ∠,CO 平分ACB ∠,过点O 作BC 的平行线与AB ,AC 分别相交于点M ,N .结论:△BOM 、△CON 都是等腰三角形。
2)角平分线加射影模型必出等腰三角形.→图4条件:如图4,BE 平分∠CBA ,∠ACB =∠CDA =90°.结论:三角形CEF 是等腰三角形。
A .20︒B .25︒【答案】B 【分析】根据作图可知AB 是CAE ∠【详解】解:∵12l l ∥,∴BCA ∠∵130BCA ∠=︒,∴50CAE ∠=︒例4.(2023.成都市青羊区八年级期中)如图,在ABC △中,90BAC ∠=︒,AD BC ⊥于点D ,ABC ∠的平分线BE 交AD 于F ,交AC 于E ,若3AE =,2DF =,则AD =_____________.【答案】5【详解】由角度分析易知AEF AFE ∠=∠,即AE AF =,∵3AE =∴3AF =∵2DF =∴5AD AF DF =+=【点睛】这道题主要讲解角平分线加射影模型必出等腰三角形的模型.例5.(2023.山东八年级期末)如图①,△ABC 中,AB =AC ,∠B 、∠C 的平分线交于O 点,过O 点作EF ∥BC 交AB 、AC 于E 、F .(1)图①中有几个等腰三角形?猜想:EF 与BE 、CF 之间有怎样的关系.(2)如图②,若AB ≠AC ,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF 与BE 、CF 间的关系还存在吗?(3)如图③,若△ABC 中∠B 的平分线BO 与三角形外角平分线CO 交于O ,过O 点作OE ∥BC 交AB 于E ,交AC 于F .这时图中还有等腰三角形吗?EF 与BE 、CF 关系又如何?说明你的理由.【答案】(1)△AEF 、△OEB 、△OFC 、△OBC 、△ABC 共5个,EF =BE +FC ;(2)有,△EOB 、△FOC ,存在;(3)有,EF =BE -FC .ABC EBO模型2、角平行线第二定理(内角平分线定理和外角平分线定理)模型1)内角平分线定理图1图2图32【点睛】本题考查角平分线的性质,三角形的面积公式,根据角平分线的性质得出A .1:1:1B .1:2:3【答案】D 【分析】过点O 作OD BC ⊥于点条角平分线,根据角平分线的性质,OA ,OB ,OC 是ABC 的三条角平分线,ABC 的三边AB 、BC 、AC 长分别为111():():(222AB OF BC OD AC =⨯⨯⨯⨯证明:过C 作AD 的平行线交AB 于点E .∵//EC AD ∴BD CD AB AE =::,∠1=∠3,∠∵AD 为∠BAC 的外角平分线∴∠1=∠2∴AE=AC ∴BD CD AB AC=::例5.(2022秋·北京·八年级北京八十中校考期中)在(3)∵AD DE =,∴由(1)知::1:1ABD EBD S S =,∵10BDE S ∆=,∴10ABD S =△,∵3,5AC AB ==,AD 平分BAC ∠,∴由(2)知:::5:3ABD ACD S S AB AC ==△△,∴6ACD S =,∴10616ABC S =+=△,故答案为:16.【点睛】本题考查了角平分线性质和三角形的面积公式,能根据(1)(2)得出规律是解此题的关键.课后专项训练A.1B.【答案】C【分析】根据三角形内角和定理可验证结论①;如图所示,在△≌△,根据全等三角形的性质可验证结论②;如图所示,连接BOE BOK(ASA)∵,AE BD 是ABC 的角平分线,∴∴在,AOD AOK △△中,AD AO ⎧⎪∠⎨⎪⎩∵,AE BD 是ABC 的角平分线,OF AC ⊥,OF n =,∴OC 平分ACB ∠,OF OG OH n ==,且AB AC BC ++=∵111222ABC AOC AOB S S S S AB OG AB OF BC OH =++++△△△△∴11(ABC S OF AB BC mn mn =++=≠,故结论③错误;∴12AOBS AO BM=△,BOES EO BM△,∴1212BOEAOBOESS OA=△△∴13BE OEAB OA==,同理,ADAB,如图所示,1BE OE A.1个B.2个【答案】C【分析】①根据角相等推出线段相等,再将线段进行转化,即可证明;AEB ∵BE 平分ABC ∠,∴EM ∵CE 平分ACD ∠,∴EN 设ACE DCE x ∠=∠=,则1802BAC z ∠=︒-,∠FCA.EC=EF B.FE=FC【答案】C【分析】求出∠CAF=∠BAF,∠是等腰三角形,而可得A .AD 是BAC ∠的平分线C .点D 在线段AB 的垂直平分线上【答案】D【分析】由作图可得:AD 30B ∠=︒,2,AB AC ∴=ACAC A BC5∠【答案】95【分析】根据角平分线的判定与性质可知【详解】解:过点D作DF1【点睛】本题考查角平分线的判定与性质,三角形的内角和定理,掌握角平分线的判定与性质是解题关键.11.(2023秋·安徽滁州·八年级统考期末)(1)如图1,当AD 平分BAC ∠时,若5AB =,延长AD 到E ,使得AD DE =,连接BE ,如果AC 【答案】53/2139AD 是BAC ∠的角平分线,5AB =,3AC =,12.(2023.广东九年级期中)如图所示,在△ABC 中,BC =6,E 、F 分别是AB 、AC 的中点,动点P 在射线EF 上,BP 交CE 于D ,∠CBP 的平分线交CE 于Q ,当CQ =13CE 时,EP +BP =________.【答案】12【解答】解:如图,延长BQ 交射线EF 于点M .E 、F 分别是AB 、AC 的中点,∴EF //BC ,∴∠CBM =∠EMBBM 平分∠ABC ,∴∠ABM =∠CBM ,∴∠EMB =∠EBM ,∴EB =EM ,∴EP +BP =EP +PM =EM CQ =13CE ,∴EQ =2CQ由EF //BC 得,△EMQ ∽△CBQ∴2 212 12EM EQEM BC EP BP BC CQ==∴==∴+=(1)求证:CDM V 是等腰三角形.【答案】(1)见解析(2)1.8【分析】(1)根据题意和图形,可以求得(2)根据勾股定理可以求得BC 的长,设∵BD 平分ABC ∠,BCD ∠=∠设CD x =,则CM x =,DF x =∴6BC BF ==,∴AF AB BF =-在Rt ADF 中222AD AF DF =+【答案】见解析【分析】根据直角三角形两锐角互余求得对等边求得CE CF =,从而求得【详解】证明:∵在ABC(2)如图2,若将(1)中“ABC 中,10AB AC ==”改为“若ABC 为不等边三角形,8AB =,10AC =”其余条件不变,则图中共有________个等腰三角形;EF 与BE 、CF 之间的数量关系是什么?证明你的结论,并求出AEF △的周长.(3)已知:如图3,D 在ABC 外,AB AC >,且BD 平分ABC ∠,CD 平分ABC 的外角ACG ∠,过点D 作DE BC ∥,分别交AB 、AC 于E 、F 两点,则EF 与BE 、CF 之间又有何数量关系呢?写出结论并证明.【答案】(1)5,EF BE CF =+,20(2)2,EF BE CF =+,证明见详解,18(3)EF BE CF =-,证明见详解【分析】(1)根据角平分线的定义可得,EBD CBD FCD BCD ∠=∠∠=∠,再根据平行线的性质,“两直线平行,同位角相等”、“两直线平行,内错角相等”可知DB DC =,AEF ABC AFE ACB ∠=∠∠=∠,,EDB CBD FDC BCD ∠=∠∠=∠,即可求出AEF AFE ∠=∠,,EBD EDB FDC FCD ∠=∠∠=∠,根据“等角对等边”可知,,BE DE CF DF AE AF ===,即可确定等腰三角形的数量,EF 与BE 、CF 之间的数量关系以及AEF △的周长;(2)若ABC 为不等边三角形,根据角平分线的定义可知,EBD CBD FCD BCD ∠=∠∠=∠,再结合平线性的性质“两直线平行,内错角相等”可知,EDB CBD FDC BCD ∠=∠∠=∠,即可推导,EBD EDB FDC FCD ∠=∠∠=∠,然后根据“等角对等边”即可证明,BE DE CF DF ==,然后解答即可;(3)根据角平分线的定义可知,EBD CBD FCD GCD ∠=∠∠=∠,再结合平线性的性质“两直线平行,内错角相等”可知,EDB CBD FDC GCD ∠=∠∠=∠,即可推导,EBD EDB FDC FCD ∠=∠∠=∠,然后根据“等角对等边”即可证明,BE DE CF DF ==,即可证明EF 与BE 、CF 之间的数量关系.【详解】解:(1)∵AB AC =,∴A ABC CB =∠∠,∵BD 平分ABC ∠,CD 平分ACB ∠,∴,EBD CBD FCD BCD ∠=∠∠=∠,∴DBC DCB ∠=∠,∴DB DC =,∵EF BC ∥,∴,AEF ABC AFE ACB ∠=∠∠=∠,,EDB CBD FDC BCD ∠=∠∠=∠,∴AEF AFE ∠=∠,,EBD EDB FDC FCD ∠=∠∠=∠,∴,,BE DE CF DF AE AF ===,∴等腰三角形有,,,,ABC AEF DEB DFC DBC ,共计5个,∴EF DE DF BE CF =+=+,即EF BE CF =+,∴AEF △的周长AE EF AF =++AE DE DF AF =+++AE BE CF AF =+++AB AC =+1010=+20=,故答案为:5,EF BE CF =+,20;(2)若ABC 为不等边三角形,∵BD 平分ABC ∠,CD 平分ACB ∠,∴,EBD CBD FCD BCD ∠=∠∠=∠,∵EF BC ∥,∴,EDB CBD FDC BCD ∠=∠∠=∠,∴,EBD EDB FDC FCD ∠=∠∠=∠,个,故答案为:,最后依据三角形内角和求解即可.小明的解法如下:过点D 作DE AB ⊥于点∵AD 是BAC ∠的角平分线,且DE AB ⊥∴,1212ABD ADCAB DES AB S AC AC DF ⨯==⨯△△,的延长线交于点于【答案】(1)DE DF =(2)见解析(3)20(4)67【分析】(1)根据角的平分线性质定理解答即可.(2)过点D 作DN AB ⊥于N ,过点D 作DM AC ⊥于M AP BD ⊥于点P .仿照第一问的解答求解即可.(3)过点D 作DN AB ⊥于N ,证明ADC ADN ≌,直接利用证明的结论,列式计算即可.(4)先算2210AC AB BC =+=,后两次运用证明的结论,依次计算即可.AC ⊥,∵AD 是NAM ∠的角平分线,∴DM DN =.∴1212ABD ADCAB DNS AB SAC AC DM ⨯==⨯,1212ABD ADCBD S S CD ⨯=⨯(3)∵Rt ABC △中,90C ∠=︒,AD 是BAC ∠∵DC DN AD AD =⎧⎨=⎩,∴ADC ADN ≌,∴∴12820AB AN BN =+=+=,故答案为:(4)解:∵90ABC ∠=︒,6AB =∵将ABC 先沿BAC ∠的平分线AD ∴6AB AE ==,BAD EAD ∠=∠∴4EC =,由(1)可得AB BD AC DC =∴13462DECS =⨯⨯=,同理可求:∴318677DEFS=⨯=,∴6FCGS =(1)请你按照以上证明思路,结合图①完成剩余的证明;(2)如图②,ABC ,①画出BAC ∠的平分线(不写画法,保留作图痕迹,使用②若BAC ∠的平分线交BC 于D ,求证:AB BDAC CD=;(3)如图③,E 是平行四边形延长,交AD 的延长线于点F ,连接,AE CF ,若ADE V 的面积为2,则CEF △②证明:如图,过点D 作DE ⊥∵AD 是BAC ∠的平分线,∴DE ∴1212ABD ACDAB DE S AB SAC AC DF ⋅==⋅,由共高定理,得:∴,EDF ECB EFD ∠=∠∠又∵AD BC =,∴DF AD ∴,DEF DEFS S =S ∴AC CD。


角平分线与平行线编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(角平分线与平行线)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为角平分线与平行线的全部内容。
专题一 角平分线与平行线一、教学目标:1、知识与技能:使学生掌握角平分线与平行线结合应用时,等量间的迁移关系。
2、过程与方法:培养学生观察图形,研究问题的能力,掌握等量代换的技巧。
3、情感态度与价值观:渗透分类讨论的思想,指导相应的学习方法,使学生不仅学会数学,而且会学数学。
二、教学重点、难点:1、教学重点:综合掌握角平分线和平行线间的关系.2、教学难点:等量关系的确定。
三、教学方法:引导发现、练习提高 四、教学手段:多媒体电脑、黑板 五、具体内容: (一)复习引入例1 如图1, 已知△ABC 中,∠BAC 的外角∠EAC 的平分线交BC 延长线于D .求证:。
设计思想:融合平行、相似、角平分线.分析:从问题来看,本题需要证明的是一个比例式,显然要与三角形“相似"挂钩,构造相似的方法可以过点C 作AD 的平行线,这样既可以有相似,又可以使“平行”、“角平分线”结合起来,构成等量关系.DC BDAC AB证明思路:过点C 作CF ∥AD 交AB 于F , 可证明AF =AC 。
由△BFC ∽△BAD得。
经等量代换得. 即。
点拨:这道题辅助线的添加是个关键,需要联系着相似和平分线两个角度来构造等腰三角形.例2 (09抚顺)已知:如图所示,直线与的平分线交于点,过点C 作一条直线与两条直线分别相交于点.(1)如图1所示,当直线与直线垂直时,猜想线段之间的数量关系,请直接写出结论,不用证明; (2)如图2所示,当直线与直线不垂直且交点都在的同侧时,(1)中的结论是否成立?如果成立,请证明:如果不成立,请说明理由; (3)当直线与直线不垂直且交点在的异侧时,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,那么线段AD 、BE 、AB 之间还存在某种数量关系吗?如果存在,请直接写出它们之间的数量关系.设计思想:这道题会用到“平行线间同旁内角角平分线形成夹角为90°”,这是关于角平分线非常普遍的应用环境之一。


高中数学中的平行线与角平分线性质在高中数学中,平行线与角平分线是两个重要的概念。
它们在几何学中具有许多有趣的性质和应用。
本文将探讨平行线与角平分线的性质,以及它们在解决几何问题中的应用。
一、平行线的性质平行线是指在同一平面内永远不相交的直线。
平行线具有以下几个重要的性质:1. 平行线的对应角相等:如果两条平行线被一条横截线所切,那么对应的内角和对应的外角相等。
2. 平行线的同位角相等:如果两条平行线被一条横截线所切,那么同位角相等。
3. 平行线的内错角互补:如果两条平行线被一条横截线所切,那么内错角互补,即相加等于180度。
这些性质是解决平行线相关问题时非常有用的工具。
通过应用这些性质,我们可以证明两条线平行,或者求解未知角度的值。
二、角平分线的性质角平分线是指将一个角分成两个相等的角的线段。
角平分线具有以下几个重要的性质:1. 角平分线与角的两边相等:角平分线将一个角分成两个相等的角,因此它与角的两边相等。
2. 角平分线的交点在角的内部:角平分线的交点必定在角的内部,而不在角的边上或外部。
3. 角平分线的交点到角的两边的距离相等:角平分线的交点到角的两边的距离相等,这个性质被称为角平分线的垂直性。
这些性质使得角平分线成为解决角相关问题的重要工具。
通过利用角平分线的性质,我们可以证明两个角相等,或者求解未知角度的值。
三、平行线与角平分线的应用平行线与角平分线的性质在几何问题的解决中有广泛的应用。
以下是一些常见的应用场景:1. 平行线的证明:通过利用平行线的性质,我们可以证明两条线平行。
例如,当两条线的对应角相等或同位角相等时,我们可以得出这两条线是平行的结论。
2. 角的平分线的应用:角平分线的性质可以帮助我们解决一些与角有关的问题。
例如,当我们需要求解一个角的大小时,可以利用角平分线将角分成两个相等的角,从而简化计算。
3. 平行线与角平分线的复合应用:在实际问题中,我们常常需要综合运用平行线与角平分线的性质。

由角平分线与平行线构成的等腰三角形在我们学习几何的过程中,有些知识点之间关系密切,往往带有一定的共性,比如当角平分线与平行线同时出现,那么一定会得到等腰三角形.下面通过几例说明“角平分线+平行线→等腰三角形”的规律,希望同学们能够举一反三,触类旁通,在解题中灵活运用.一、基本图形(分两种情况):1.平行线平行于角的一边,如图1,OC 平分∠AOB ,CD ∥OB. 则DO=DC,2.平行线平行于角的平分线,如图2,OC 平分∠AOB ,OC ∥BD.则OD=OB.二、应用举例例1.如图3,在△ABC 中,若AD 平分∠BAC ,交BC 于D,DE ∥AB ,则△ADE 是等腰三角形.证明:如图3,∵AD 平分∠BAC ,∴∠BAD =∠CAD ,∵DE ∥AB ,∴∠BAD =∠ADE ,∴∠CAD =∠ADE ,∴AE =DE ,即△ADE 为等腰三角形.变式1:如图4,在△ABC 中,AD 平分∠BAC ,交BC 于D,CE ∥AB ,则△ACE 是等腰三角形;变式2:如图5,在△ABC 中,AD 平分∠BAC ,交BC 于D, BE ∥AC ,则△A BE 是等腰三角形.仿例1可以给出证明.例2.如图6,在△ABC 中,AD 平分∠BAC ,交BC 于D,CE ∥AD ,则△ACE 是等腰三角形.证明:∵AD 平分∠ABC , ∴∠1=∠2,AEB CD图3图5 AE BCD图4 AEBCD图1图2∵CE ∥AD ,∴∠2=∠3,∠1=∠E , ∴∠3=∠E ,∴AC =CE.变式1:如图7,在△ABC 中,AD 平分∠BAC ,交BC 于D,EF ∥AD ,交AC 于点G ,交BA 延长线于E,则△AEG 是等腰三角形.变式2:如图8,在△ABC 中,若AD 平分∠BAC ,交BC 于D, EF ∥AD ,交BC 于F ,交CA 的延长线于G ,则△AEG 是等腰三角形.这些基本规律在解题中有一定的指导作用.例3.如图9,在△A BC 中,∠ABC 与∠ACB 的平分线交于点D ,过点D 作EF ∥BC 交AB 于E ,交AC 于F ,(1)求证:EF =BE +CF .(2)若AB=9,AC=8,求△AEF 的周长.分析:观察图形,看到EF 已被点D 分成了两条线段(DE 和DF),而条件中恰好具备“角平分线+平行线”,可得到两个等腰三角形△BDE 和△CDF ,于是可分别证明DE =BE ,DF =CF 即可.(1)证明:∵BD 平分∠ABC ,∴∠1=∠2, ∵EF ∥BC ,∴∠3=∠2, ∴∠1=∠3,∴BE =DE , 同理DF =CF ,∴DE +DF =BE +CF ,即EF =BE +CF (2)由(1)得:△AEF 的周长 =AE+AF+EF =AE+AF+(BE +CF) =AB+AC =9+8 =17.上述两例都是由角平分线、平行线构成的等腰三角形,并且同时出现两个,而这个发现是突破此类问题难点的关键.例4.如图10,在平行四边形ABCD 中,∠ABC 的平分线交AD 于点E ,∠BCD 的平分线交AD 于点F ,BE 、CF 交于点G ,,AEB CD F G图7BCDFE AG 图8)13(AE BCF D 图9)2A EB CD)1)2图6(1)求证:AF=DE,(2)若AB=3,BC=4,FG=1,求∠A 的度数. (3) 若△EFG 为等腰直角三角形,求∠A 的度 数.解:(1)在平行四边形ABCD 中 ∵AD ∥BC, ∴∠2=∠5,又 ∠2=∠5, ∴∠1=∠5,∴AE=AB, 同理可证:DF=CD. ∵AB=CD ∴AE=DF .∵ AF=AE -EF; DE=DF-EF , ∴AF=DE.(2)在平行四边形ABCD 中,设BE 与CF 交于点G,, ∵AB ∥CD ,∴∠ABC+∠BCD=180°,∵BE 平分∠ABC ,CF 平分∠BCD ,∴12,2ABC ∠=∠ 13,2BCD ∠=∠ 123()902ABC BCD ∠+∠==∠+∠=°,∴∠BGC=90°,即BE ⊥CF ; 因为AD=BC=4,DF=DC=3,∴AF=AD-DF=4-3=1; 又AF=AE -EF; ∴1=3-EF , ∴EF=2.又∵FG=1,∴1,2FG EF =∴∠5=30°,∵AE=AB ,∠1=∠5=30°, ∴∠A=120°. (3)由(2)得∠BGC=90°,∴∠EGF=90°,若△EFG 为等腰直角三角形,则∠5=45°,∴∠1=∠5=45°, ∴∠A=90°.评注:①此题关键在于利用角平分线、平行线发现两个等腰三角形,即△ABE 和△DCF,②利用平行四边形的对边相等,分别得到AF=DE=1,③利用平行线的性质得到Rt △BGC ,Rt △EGF , ④如果直角边为斜边的一半则直角边所对的角为30°.例5.已知:如图11,在△ABC 中,AD 平分∠BAC,EF ∥AB 交BC 于E 、交AD 于F ,若DE=DC.求证:EF=AC.证明:过作CM ∥EF ,交AD 的延长线于M ,连结CM ,则∠M=∠3,,ABCDFE G)2)1 4(3(5(图10图11∠EDF=∠CDM ,又 DE=DC. ∴△EDF ≌△C DM , ∴EF=CM. ∵ EF ∥AB ,∴∠3=∠1,又∠1=∠2,∴ ∠M=∠2,∴AC=CM , 从而EF= AC.评析:本题的关键在于作通过添加平行线构成以AC(或EF)为腰的等腰三角形,再证EF=CM.通过上述例题,我们发现,尽管每道题目的结论各异,但每道题中都有角平分线、平行线,故都可得等腰三角形这一共性.所以,在学习过程中,要善于发现、总结规律.真正驳清了基本概念,变成一个个知识板块,其本质属性理解透彻,就能收到举一反三,融会贯通的效果.附:参考习题1.如图12,在△ABC中,O是∠ABC、∠ACB的角平分线的交点,OD∥AB,交BC于点D,OE∥AC,交BC于点E,若BC=10cm ,求△DOE 的周长,2.如图13,在△ABC 中,∠ABC 的平分线与∠ACB 的外角∠ACP 的平分线交于D 点,过点D 作EF ∥BC ,交AB 于E ,交AC 于F ,求证:EF =EB -FC3.如图14:平行四边形ABCD 中,∠ABC 的平分线交AD 于E ,∠BCD 的平分线交AD 于F ,且AB=3,DE=2,(1)求平行四边形ABCD 的周长.(2)求证:BE ⊥CF (3)若CF=2,求BE 的长..参考答案:1.△DOE 的周长为10cm ; 2.证明略;3.(1)平行四边形ABCD 的周长为16;(2)证明略;(3)BE=22226242BE BN EN =-=-=.AE B COD图12 )1 )2 4(图14A EBCFDP图13。

平面几何的平行线与角平分线在平面几何中,平行线和角平分线是两个基本的概念。
它们在解决许多几何问题和证明中起着重要的作用。
本文将介绍平行线和角平分线的定义、性质以及应用。
一、平行线的定义与性质1.1 定义在平面上,如果两条直线在同一平面内没有交点,我们称它们为平行线。
用符号“∥”表示平行关系。
例如,若AB∥CD,则表示线段AB 与线段CD平行。
1.2 性质(1)平行线的性质1:平行线具有传递性。
如果AB∥CD且CD∥EF,则有AB∥EF。
(2)平行线的性质2:平行线与一直线的交线上的对应角相等。
(如图1所示)图1:平行线与对应角(3)平行线的性质3:平行线与一直线的交线上的内错角互补,即内错角和为180°。
(如图2所示)图2:平行线与内错角1.3 平行线的应用平行线的概念与性质在几何问题的解决中有着广泛的应用。
以下是一些例子:(1)构建平行线:在给定线段上作一条与给定直线平行的线段。
(2)判定平行线:通过已知条件判断两条直线是否平行。
(3)平行线截图定理:若两条直线被平行线切割,则对应的线段成比例。
二、角平分线的定义与性质2.1 定义在平面上,如果一条直线将一个角分成两个相等的角,我们称这条直线为角的平分线。
如图3所示,线段DE是∠C的角平分线,∠CED与∠DEB是相等的。
图3:角平分线2.2 性质(1)角平分线的性质1:角平分线将角分成相等的两个角。
(2)角平分线的性质2:角平分线与角的对边垂直。
(如图4所示)图4:角平分线与对边垂直2.3 角平分线的应用角平分线的概念与性质在实际问题中有着广泛的应用。
以下是一些例子:(1)角平分线的构造:给定一个角,作出它的角平分线。
(2)判定角平分线:通过已知条件判断一条直线是否为角的平分线。
(3)角平分线的性质在解决相关角度关系的问题中起着重要的作用,如证明两条直线平行等。
结论平面几何中的平行线和角平分线是重要的概念,它们在解决几何问题和证明中起着重要的作用。
角平分线模型模型 4 角平分线+平行线如图,P 是∠MON 的平分线上一点,过点 P 作 PQ∥ON,交 OM 于点 Q。
结论:△POQ 是等腰三角形。
模型证明∵PQ∥ON∴∠PON=∠OPQ又∵OP 是∠MON 的平分线∴∠POQ=∠PON∴∠POQ=∠OPQ∴△POQ是等腰三角形模型分析有角平分线时,常过角平分线上一点作角的一边的平行线,构造等腰三角形,为证明结论提供更多的条件,体现了角平分线与等腰三角形之间的密切关系。
模型实例解答下列问题:(1)如图①所示,在△ABC 中,EF∥BC,点 D 在 EF 上,BD、CD 分别平分∠ABC、∠ACB,写出线段 EF 与 BE、CF 有什么数量关系;(2)如图②所示,BD 平分∠ABC、CD 平分∠ACG,DE∥BC 交 AB 于点 E,交 AC于点 F,线段 EF 与 BE、CF 有什么数量关系?并说明理由。
(3)如图③所示,BD、CD 分别为外角∠CBM、∠BCN 的平分线,,DE∥BC 交AB 延长线于点 E,交 AC 延长线于点 F,直接写出线段 EF 与 BE、CF 有什么数量关系?解析:(1)由模型可知,ED=BE,DF=CF∴EF=ED+DF=BE+CF(2)∵DE∥BC∴∠EDB=∠DBC又BD 平分∠ABC∴∠DBE=∠DBC∴∠EDB=∠DBE∴△EBD为等腰三角形∴BE=ED同理可证:FD=CF∴EF=ED-FD=BE-CF∴EF=BE-CF(3)EF=BE+CF(由模型可轻松证明)模型练习1.如图,在△ABC 中,∠ABC、∠ACB 的平分线交于点E,过点E作MN∥BC,交 AB 于点 M,交 AC 于点 N。
若 BM+CN=9,则线段 MN 的长为。
解析:由模型可得,ME=BM,EN=CN∴MN=ME+EN=BM+CN=92.如图,在△ABC 中,AD 平分∠BAC,点 E、F 分别在 BD、AD 上,且 DE=CD,EF=AC 求证:EF∥AB。
平行线及角平分线类相似中考要求重难点1.相似定义,性质,判定,应用和位似2.相似的判定和证明3.相似比的转化课前预习上一节课我们知道了相似三角形的由来,那你是否知道其他跟金子塔有关的不可思议的事实呢?不仅建造金字搭的技术中,表现了古埃及人的非凡的数学天才;而且,它本身的许多数据,也说明了古埃及人的数学才华,巧夺天工,比如,胡夫金字塔底面周长365米,恰好是一年的天娄;周长乘以2,正是赤道的时分度;搭高乘以10九次方,正是地球到太阳的距离;周长除以塔塔高的2倍,正是圆周率3.1415926……;塔的自重乘以10的15次方,正好是地球的重量;塔里放置的棺材內部尺寸,正好是几千年后希腊数学家华连哥拉斯发现华连哥拉斯数——345::.数学的趣味是无法言语的,同学们可以从身边的点滴去发现其中的奥秘.例题精讲模块一 平行线类相似平行线类相似的基本模型有【例1】 如图,在ABCD 中,点E 在线段DC 上,若12DE EC =∶∶,则BF BE =∶ .EAD BCF【难度】1星【解析】过E 点作AD 的平行线交AC 于H ,可求出结果.HFCBD AE【答案】35∶【巩固】如图,在ABC △中,,,DE BC DG AC CF AB ∥∥∥,则图中与ABC △相似的三角形(ABC △除外)有哪些?GFA BCDE【难度】1星【解析】根据三角形相似的判定定理,可知道ABC ADE DBG FCG △∽△∽△∽△ 【答案】ABC ADE DBG FCG △∽△∽△∽△【拓展】如图,点1234,,,A A A A 在射线OA 上,点123,,B B B 射线OB 上,且112233A B A B A B ∥∥,21A B ∥32A B43A B ∥.若212323,A B B A B B △△的面积分别为1,4,则图中三个阴影三角形面积之和为 .4321【难度】3星【解析】由平行得到相似的三角形.已知212A B B △△A 2B 1B 2,323A B B △的面积分别为1,4,且两三角形相似,因此可得出223312A B A B =,由于223A B A △与233B A B △是等高不等底的三角形,所以面积之比即为底之边比,因此这两个三角形的面积比为1:2,根据323A B B △的面积为4,可求出223A B A △的面积,同理可求出334A B A △和112A B A △的面积.即可求出阴影部分的面积.【答案】10.5∵212A B B △,323A B B △的面积分别为1,4 又∵22332132,A B A B A B A B ∥∥∴2233212323,OB A OB A A B B A B B ∠=∠∠=∠ ∴122233B B A B B A △∽△ ∴1222233312B B A B B B A B == ∴233412A A A A = ∵22323322323331,4A B A B A B S A B A B B S A B ==△△△的面积是4 ∴223323122A B A A B B S S ==△△(等高的三角形的面积的比等于底边的比)同理可得:3343232248A B A A B B S S ==⨯=△△,1122121110.522A B A A B B S S ==⨯=△△∴三个阴影面积之和为0.52810.5++=.【例2】 如图,已知DE AB ∥,2OA OC OE =⋅,求证:AD BC ∥.DOECB A【难度】2星【解析】由一个平行得到比例线段OE ODOA OB=,再根据已知条件2OA OC OE =⋅,以及线段间的等量代换得到OD OAOB OC=,得到证明AOD COB ∆∆∽,得到相等的角DAO BCO ∠=∠,最后得到证明AD BC ∥. 【答案】∵DE AB ∥∴AOB EOD ∆∆∽,OE ODOA OB=, 又∵2OA OC OE =⋅, ∴OE OAOA OC =, ∴OD OAOB OC=, ∵AOD COB ∠=∠, ∴AOD COB ∆∆∽, ∴DAO BCO ∠=∠, ∴AD BC ∥【巩固】在平行四边形ABCD 中,点E 为AD 的中点,连接BE ,交AC 于点F ,则AF CF ∶=( )FED CBA【难度】2星【解析】根据四边形ABCD 是平行四边形,求证AFE BCF △∽△,然后利用其对应边成比例即可求得答案.【答案】12∶∵四边形ABCD 是平行四边形, ∴AFE BCF △∽△, ∴AE AFBC CF=,∵点E 为AD 的中点, ∴12AE AF BC CF ==,【巩固】如图,在ABC ∆的边AB 上取一点D ,在AC 取一点E ,使AD AE =,直线DE 和BC 的延长线相交于P ,求证:BP BDCP CE=. PEDCBA【难度】2星【解析】根据所要证明的结论,由三点定形法可初步判定需要证明PCE PDB △∽△,但根据所给的已知条件无法找到有利的条件得到证明,于是回到题中看看怎么样能利用到已知条件AD AE =,于是尝试着过C 作平行线得到证明.4321MPE D CBA【答案】过C 作CM AB ∥交DP 于M ,∵CM AB ∥, ∴PCM PBD ∆∆∽, ∴BP BDCP CM=, ∵CM AB ∥, ∴14∠=∠, 又∵AD AE =,∴12∠=∠,∴24∠=∠, ∵23∠=∠, ∴34∠=∠, ∴CM CE = ∴BP BDCP CE=【拓展】如图,在ABC △中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BCCD=____ ___. MECBA【难度】3星【解析】先介绍常规的解法:BCFE DMA BCFED M A如图,过点C 作DE 或AB 的平行线均可,不妨以左图为例来说明. 过点C 作//CF DE ,交AB 于点F . ∵AM MC =,//CF DE ∴AE EF = ∵14AE AB =∴2BF EF= ∵//CF DE ∴2BC BFCD EF== 当然,过点M 、点E 作适当的平行线,均可作出此题,这里不再给出. 以上这些解法均属于常规解法,下面介绍特殊的解法: 看ABC ∆为直线EM D 所截,由梅涅劳斯定理可知,1AE BD CM EB DC MA⋅⋅= 又14AE AB =,AM CM =,故32BD BC DC CD=⇒= 上述图形是一个经典的梅氏定理的基本图形,解类似的题时,梅氏定理的运用能够带来立竿见影的效果,很快得出答案,梅氏定理的证明见变式1,先讲变式1再介绍本解法.【答案】2【拓展】如图,AD 是ABC △的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.AB CDEF【难度】3星【解析】1()过点D 、E 、F 作平行线均可构造出平行线的基本图形,然后利用 这些基本图形的性质来解题.以下给出6种辅助线(还有几种没给 出),解题过程不再给出.HAB C DEF ABCD EF HHAB CDEFHAB CD EFHAB CDEFHABCD EF当然,本题也可由梅氏定理直接得出结果. 看ADC ∆被直线BEF 所截,由梅氏定理可得1AF CB DEFC BD EA⋅⋅= 又AE DE =,BD CD =,故12AF FC =. 2()结论依然成立,解法同上(包括用梅氏来解题),不再给出. 【答案】1()见解析;2()结论依然成立模块二 角平分线类相似问题角平分线类的相似模型如下:方法点播:角平分线类得相似问题基本就这样的两种模型,辅助线的做法也如图中虚线所示,学生在学这部分知识时,不管是平时测验和期中、期末考试,只要涉及到角平分线和证明相似问题就可以试着做这样的辅助线,基本都可以解决.【例1】 如图,AD 是ABC △的角平分线,求证:AB BDAC CD=D CB A【难度】3星【解析】由角平分线类的相似模型可作出辅助线:过点C 作CE AD ∥交直线AB 于E ,再根据平行得到相似的比例线段,最后题目得证.321EDCBA【答案】过C 作CE AD ∥交直线AB 于E .∵CE AD ∥, ∴1E ∠=∠,23∠=∠ 又∵AD 平分BAC ∠, ∴12∠=∠, ∴3E ∠=∠, ∴AE AC =,由CE AD ∥可得:AB BDAE CD=, ∴AB BDAC CD=【巩固】 已知ABC △中,BAC ∠的外角平分线交对边BC 的延长线于D ,求证:AB BDAC CD=DCBA【难度】4星【解析】由外角平分线证明相似的模型可作辅助线:过C 作CE AD ∥交直线AB 于E ,根据平行得到成比例线段AB BD AE CD =,再根据角与角相等的等量代换证明AE AC =,结论得证AB BDAC CD=. F 4321E DCBA【答案】过C 作CE AD ∥交直线AB 于E∵CE AD ∥, ∴13∠=∠,24∠=∠ 又∵AD 平分CAF ∠, ∴12∠=∠, ∴34∠=∠, ∴AE AC =, 由CE AD ∥可得:AB BDAE CD=, ∴AB BDAC CD=【巩固】在Rt ABC △中,线段CE 平分ACB ∠交AB 于点E ,交斜边上的高AD 于点O ,过O 引BC 的平行线交于F .求证:AE BF =.321OF E DCBA【难度】3星【解析】在相似问题中遇到证明线段相等的问题时一定要能想到:这个证明可能是由两组成比例线段进行等量代换得到.本题由角平分线得到角相等再由都是直角三角形,可证明一组相似三角形得到一组成比例线段CD AC OD AE =,再根据平行线分三角形两边成比例得到比例线段ADABOD BF =,最后再根据一组相似三角形得到成比例线段AD AB CD AC =,等量代换得到ODBFOD AE =,题目得证AE BF =.【答案】∵CE 平分ACB ∠∴23∠=∠∴Rt CAE Rt CDO △∽△ ∴CDACOD AE =又∵OF BC ∥ ∴ADABOD BF =又∵Rt ABD Rt CAD △∽△ ∴AD AB CD AC =,即ODBFOD AE =∴AE BF =注意:应用比例线段证明两直线平行或两线段相等时,(1)要注意如果相关的比例式较多,一时难以作出选择,应将所有相关的比例式都写出来,然后再仔细对比、分析选出有用的。
第7讲 相似三角形综合【学习目标】相似三角形是初中数学中的重点,也是难点.相当多的知识点可以与相似三角形综合起来考察.本讲将从以下几个方面学习相似三角形的应用,旨在灵活运用相似三角形的判定和性质解决问题.【基础知识】1、平行线与相似三角形利用平行线构造的相似主要有两个基本的模型,即:“A ”字型和“X ”字型.2、角平分线与相似三角形角平分线类的相似模型如下:分为“内角平分线”和“外角平分线”两种类型,虚线部分为辅助线的作法. 3、a 2 = b·c 与相似三角形 常见及扩展模型如下:由图1可证:2AB BD BC =;由图2可证:2AB BD BC =,2AD BD DC =,2AC CD CB =.4、内接矩形与相似三角形 相关模型:常用结论:.5、一线三等角与相似三角形相关模型如下图所示:【考点剖析】考点一:平行线与相似三角形例1.过ABC ∆的顶点C 任作一直线,与边AB 及中线AD 分别交于点F 、E .求证:2AE AFED FB= .【难度】★★【解析】过点D 作//DG AB 交CF 于点G .//DG AB ,;AD 是中线, 2BC CD =, ;2AE AFED BF=. 【总结】题考查三角形一边的平行线知识,要学会构造平行基本模型. 例2. 如图,已知ABC ∆中,AD 、BE 相交于G ,:3:1BD DC =,:1:2AG GD =.求:BG GE 的值.【难度】★★ 【答案】11.【解析】点G 作//GM BC 交AC 于点M .//GM BC ,;:1:2AG GD =, ,:3:1BD DC =,,,,:BG GE 的值为11.【总结】本题考查了三角形一边的平行线知识,要学会构造平行基本模型.例3.如图,在ABC ∆中,点D 在线段BC 上,75BAD ∠=︒,30CAD ∠=︒,AD = 2,BD = 2DC,求AC的长.【难度】★★【答案】3.【解析】过点D作//DM AB交AC于点M.DM AB,;//又,30∠=CADAMD∠=,AM D ADM75∠=∠,==.2AD AMDM AB,.//又2=,.BD DCAC=.3【总结】本题考查了三角形一边的平行线及等腰三角形的相关知识.考点二:角平分线与相似三角形例1.如图,AD是ABC∆的内角平分线.求证:.【难度】★★【解析】过点C作//CM AB交AD的延长线于点M.CM AB//,BAD M∠=∠AD是角平分线∠=∠;BAD DAC∠=∠M DAC=AC CM.【总结】本题考查了三角形一边的平行线、角平分线及等腰三角形的相关知识.例2.如图,在ABC∠的平分线AD∠=∠过点C作CE // AB,交CAB∆中,90CAB∠=︒,CFG B于E.(1)不添加字母,找出图中所有的相似三角形,并证明;(2)求证:.【难度】★★【解析】 (1)①ADB EDC ∆∆∽、②CAB GCF ∆∆∽.证明①: //CE AB ADB EDC ∆∆∽证明②://CE AB 180CAB ACE ∴∠+∠=,90CAB ∠=,90ACE ∴∠=;CAB ACE ∴∠=∠ CAB GCF ∆∆∽ (2)由CAB GCF ∆∆∽得ADB EDC ∆∆∽ AB ADEC DE=//CE AB ,CAE EAB ∠=∠, ;CAE E ∴∠=∠, CA CE ∴=AB ADAC DE=. 【总结】本题考查相似三角形的判定和性质等知识. 考点三:a 2 = b·c 与相似三角形例1.如图,Rt ABC ∆中,,AD BC ⊥于点D .求证:2AD BD DC =.【难度】★【解析】AD BC ⊥, . 90BAD B ∠+∠=. 90BAC ∠= ,90C B ∠+∠=, BAD C ∠=∠.ABD CAD ∆∆∽ ,.2AD BD CD =•.【总结】本题考查相似三角形的性质及判定等知识.例2.如图,已知等腰三角形ABC 中,AB = AC ,高AD ,BE 相交于点H .求证:24DH DA BC =.【难度】★★【解析】AD 、BE 是高, . 90HBD C ∠+∠=, 90CAH C ∠+∠=., HBD CAD ∆∆∽.即DH AD BD CD =, 12BD DC BC ==.BAD C ∠=∠.214DH AD BC =, 24DH AD BC =. 【总结】本题考查“双高”模型相似的知识.例3.如图,在直角梯形ABCD 中,AB // CD ,AB ⊥BC ,对角线AC ⊥BD ,垂足为E , AD = BD ,过E 的直线EF // AB 交AD 于点F . (1)AF = BE ; (2)AF 2 = AE ·EC .【难度】★★【解析】(1)//EF AB ,AF 不平行EB ,四边形FABE 是梯形.又AD BD =, DAB DBA ∠=∠. 四边形FABE 是等腰梯形, AF BE =; (2),, .EBA ECB ∠=∠. EBA ECB ∆∆∽. .2EB EA EC =•,2AF EA EC =•.【总结】本题考查等腰梯形及相似三角形的判定及性质. 考点四:内接矩形与相似三角形例1.如图,ABC ∆中,3AC =,4BC =,90C ∠=︒,四边形DEFG 为正方形,其中D 、E 在边AC 、BC 上,F 、G 在AB 上,求正方形DEFG 的边长.【难度】★★ 【答案】.【解析】设正方形DEFG 的边长为a ,过点C 作CH AB ⊥交AB 于点H ,易知:////DG CH DE AB , ,在Rt ABC ∆中,34AC CB ==,, 5AB ∴=,125CH =.11255a a ∴+=, 6037a ∴=, 正方形DEFG 的边长为. 【总结】本题考查三角形内接正方形的模型,熟练掌握此题涉及的知识点. 考点五:一线三等角与相似三角形例1.已知,在等腰ABC ∆中,AB = AC = 10,以BC 的中点D 为顶点作EDF B ∠=∠, 分别交AB 、AC 于点E 、F ,AE = 6,AF = 4,求底边BC 的长.【难度】★★ 【答案】46. 【解析】, 而, .又EDF B ∠=∠,.AB AC =,B C ∠=∠. . ., 24DC BD ∴=.又12CD DB BC ==, 46BC ∴=.【总结】本题是对“一线三等角”模型的考查. 考点六:旋转与相似三角形例1.如图,直角梯形ABCD 中,,AD // BC ,BC = CD ,E 为梯形内一点,且,将BEC ∆绕点C旋转90°使BC 与DC 重合,得到DCF ∆,联结EF 交CD 于M .已知BC = 5,CF = 3,则DM : MC 的值为( )A .53B .35C .43D .34【难度】★★ 【答案】C . 【解析】旋转后,.5CB CD ∴==, 3CE CF ==,BE DF =, .在Rt CBE ∆中,222BE CE BC +=, 4BE ∴=.4DF ∴=.90ECF ∠=,. 又//CE DF ∴.【总结】本题考查旋转的相关知识,平行的判定、三角形一边的平行线的知识. 考点七:函数与相似三角形例1.如图,已知ABC ∆与ADE ∆都是等边三角形,点D 在BC 边上(点D 不与B 、C重合),DE 与AC 相交于点F . (1)求证:ABD ∆∽DCF ∆;(2)若BC = 1,设BD = x ,CF = y ,求y 关于x 的函数解析式及定义域;(3)当x 为何值时,79AEF ABD S S ∆∆=?【难度】★★【解析】(1)ABC ∆、ADE ∆是等边三角形60,60B C E EDA ∴∠=∠=∠=∠=,CDF DAB ∴∠=∠ ;(2)由(1)得ABD DCF ∆∆∽, 11x x y∴=-()201y x x x ∴=-+<<;(2)易证ABD AEF ∆∆∽,ADE ∆是等边三角形 AD AE ∴=1AB = 79AF ∴= 72199y CF ∴==-=, 229x x ∴-+=解得1221,33x x == 当2133x x ==或时,79AEF ABD S S ∆∆=.【总结】本题考查旋转的相关知识,“一线三等角”模型,相似的性质等的相关知识.【过关检测】一、单选题1.(2019·上海)如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O )20米的点A 处,沿OA所在的直线行走14米到点B时,人影的长度( )A.增大1.5米B.减小1.5米C.增大3.5米D.减小3.5米【答案】D试题分析:设小明在A处时影长为x,B处时影长为y.∵AC∥OP,BD∥OP,∴△ACM∽△OPM,△BDN∽△OPN,∴,,则,∴x=5;,∴y=1.5,∴x﹣y=3.5,故变短了3.5米.故选D.2.(2019·上海)如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE•平分∠ABC,则下列关系式中成立的有( )①;②;③;④CE2=CD×BC;⑤BE2=AE×BCA.2个B.3个C.4个D.5个【答案】B【分析】根据角平分线的性质,推出角相等,再得出边相等,判断出①②正确,再利用三角形不相似,排除其它选项,最后得解.【详解】解:如图,∵BE平分∠ABC,CE平分∠BCD∴∠ABE=∠CBE,∠ABE=∠CBE.∵CD∥BA,∴∠ABC+∠BCD=180°.∴∠BEC=∠D=∠A=90°.则有△CED∽△BEA∽△CBE,∴①正确,③正确;无法证明CD=DE,故②不正确;故④CE 2=CD×BC正确;故BE2=AE×BC不正确.因此只有①②④正确.故选B.【点睛】本题利用了平行线的性质,角的平分线的性质,等边对等角,相似三角形的判定和性质求解.二、填空题3.(2019·上海民办桃李园实验学校)在ABC中,6BC=,G是ABC的重心,过G作边BC的平行线交AC于点H,则GH的长为_________.【答案】2【详解】连接AG,并延长AG交BC于D;根据重心的性质知:D是BC中点,且AG:AD=2:3;可根据平行线分线段成比例定理得出的线段比例关系式及CD的长求出GH的值.解:如图,连接AG,并延长AG交BC于D;∵G是△ABC的重心,∴AG:GD=2:3,且D是BC的中点;∵GH∥BC,∴;∵CD=12BC=3,∴GH=2.“点睛”此题考查了平行线分线段成比例定理以及重心的概念和性质:三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.4.(2019·上海)如图,M是▭ABCD的AB的中点,CM交BD于E,则图中阴影部分的面积与▱ABCD 的面积之比为_____.【答案】1:3试题解析:设平行四边形的面积为1,∵四边形ABCD是平行四边形,∴12DAB ABCDS S=,又∵M是ABCD的AB的中点,则1124DAM DAB ABCDS S S==,∴EMB △上的高线与DAB 上的高线比为 ∴1113212EMBDABS S =⨯=, ∴143DECMEBSS,== S 阴影面积则阴影部分的面积与▱ABCD 的面积比为13. 故填空答案:13. 5.(2019·上海市民办新北郊初级中学九年级期中)如图,在ABC 中,点D 、E 分别在AB 、AC 上,且DE BC ∥,若4ADE S =△,3BDES =,那么:DE BC =______.【答案】4:7【分析】根据,得到 ,通过△ADE ∽△ABC ,根据相似三角形的性质得到DE :BC=AD :AB=4:7. 【详解】解:∵S △ADE =4,S △BDE =3 ∴ ∴∵DE ∥BC , ∴△ADE ∽△ABC , ∴DE :BC=AD :AB=4:7. 故答案为4:7.【点睛】本题考查了相似三角形的判定和性质,知道不等底同高的三角形的面积比等于底的比是解题的关键.6.(2021·上海九年级专题练习)在方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图,请在边长为1个单位的2×3的方格纸中,找出一个格点三角形DEF .如果△DEF 与△ABC 相似(相似比不为1),那么△DEF 的面积为______.【答案】1;【分析】根据小正方形的边长,分别求出ABC 和DEF 三边的长,然后判断它们是否对应成比例,再用三角形面积公式求解即可.【详解】如图,∵1AB BC ==,,AC =∴∵DE =2EF =,DF =∴∴∴~ABC DEF ∴12112DEF S =⨯⨯= 故答案为:1【点睛】本题考查了在网格中画与已知三角形相似的三角形、三角形全等的判定以及三角形面积公式,熟练掌握三角形全等的判定是解题的关键.7.(2019·上海九年级期中)如图,在△ABC 中,AC =2,BC =4,D 为BC 边上的一点,且∠CAD =∠B . 若△ADC 的面积为a ,则△ABD 的面积为____________【答案】3a【分析】通过证明△ACD ∽△BCA ,由相似三角形的性质求出△BCA 的面积为4a ,计算即可.【详解】解:∵∠CAD=∠B ,∠ACD=∠BCA ,∴△ACD ∽△BCA ,∴ , ∴14BCA a S =△, 解得,△BCA 的面积为4a ,∴△ABD 的面积为:4a-a=3a ,故答案为:3a .【点睛】本题考查的是相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.三、解答题8.(2019·上海市民办嘉一联合中学九年级月考)如图,61620AB BD,CD BD,AB ,CD ,BD ⊥⊥===,动点P 从B 向D 运动,当PAB ∆与PCD ∆相似时,试求BP 的长度.【答案】或8或12【分析】设BP =x ,由BD -BP 表示出PD ,分两种情况考虑:当△P AB ∽△PCD 时;当△P AB ∽△CPD 时,分别由相似得比例,将各自的值代入列出关于x 的方程,求出方程的解得到x 的值,即为PB 的长.【详解】解:设BP =x ,BD =20,则PD =BD -BP =20-x ,分两种情况考虑:假设△P AB ∽△PCD ,有,又AB =6,CD =16,∴,即6(20-x )=16x , 解得:6011x =; 假设△P AB ∽△CPD ,有,∴,即x (20-x )=96,整理得:(x -12)(x -8)=0,解得:x 1=12,x 2=8,综上,当P 离B 的距离为或8或12时,△P AB 与△PCD 是相似三角形.【点睛】此题考查了相似三角形的判定,利用了分类讨论的思想,相似三角形的判定方法为:两对对应角相等的两三角形相似;三边对应成比例的两三角形相似;两边对应成比例且夹角相等的两三角形相似. 9.(2017·上海九年级月考)已知:如图,直线y=kx+2与x 轴的正半轴相交于点A (t,0)、与y 轴相交于点B ,点C 在第三象限内,且AC ⊥AB ,AC=2AB .(1)当t=1时,求直线BC 的表达式;(2)点C 落在直线:y=-3x-10上,求直线CA 的表达式.【答案】(1)423y x =+ (2)y=x-2 【解析】(1)先证ΔAOB ∽ΔACH 求出C 点的坐标,设BC 为y=k 1x +b 将B 、C 代入即可求出直线BC 的表达式;(2)由(1)可知ΔAOB ∽ΔACH ,求出A 、C 的坐标代入AC 为,即可求出直线CA 的表达式. 解:(1)过H 作CH ⊥x 轴,垂足为H ,由题意得,当t=1时,A(1,0),OA=1,B (0,2),OB=2AC ⊥AB ,∠BAC=90°,∠BAO+∠CAH=90°∠BAO+∠OBA=90°∠ABO=∠CAH在ΔAOB 与ΔACH 中,∠ABO=∠CAH∠AOB=∠CHA 与ΔAOB ∽ΔACHCH=2,AH=4,C(-3,-2)设BC 为y=k 1x +b,代入B (0,2),C(-3,-2)得,解得,(2)由(1)可知ΔΔAOB ∽ΔACHCH=2t,AH=4,C(t-4,-2t)又C 在直线:y=-3x-10上,t=2C (-2,-4),A (2,0)设AC 为,代入A (2,0),C(-2,-4),解得,10.(2020·上海九年级一模)如图,在ABC ∆中,点,,,D E F G 分别在,,AB AC BC 上,3AB AD =,2CE AE =,,DG 与EF 交于点H .(1)求证:;(2)连接,DF EG ,求证:.【分析】(1)根据已知条件先证明DG ∥AC ,EF ∥AB ,可得∠HGF=∠C ,∠HFG=∠B ,即可证明△HFG ∽△ABC ,从而可得结论;(2)连接DF,EG,DE,证明四边形DFGE和ADHE是平行四边形,即可证得结论.【详解】∵AB=3AD,BF=FG=CG,∴BD=2AD,BG=2CG,∴,∴DG∥AC,同理可得,EF∥AB,∴∠HFG=∠ABC,∠HGF=∠ACB,∴△HFG∽△ABC,∴,即;DF EG,DE,如图所示,(2)连接,∵EF∥AB,∴,∵GF=FB∴=1,∴GH=HD,同理可证,FH=EH,∴四边形DFGE是平行四边形,∴DF∥EG,∴∠FDG=∠EGD,∴∠FHG=∠EGH+∠HEG,∵∠DHE=∠FHG,∠+∠,∴∠DHE=∠EGH+∠HEG=FDG GEF由EF∥AB,DG∥AC,得四边形ADHE是平行四边形,∴∠A=∠DHE,∴【点睛】此题主要考查了平行线分线段成比例的判定与性质,以及平行四边形的判定与性质,熟练掌握相减的判定与性质是解决此题的关键.a b c=.11.(2021·上海九年级专题练习)已知:::2:3:5(1)求代数式的值;(2)如果324a b c -+=,求,,a b c 的值.【答案】(1)1;(2)6,9,15a b c ===【分析】(1)设a=2k ,b=3k ,c=5k ,代入代数式,即可求出答案;(2)把a 、b 、c 的值代入,求出即可.【详解】∵::2:3:5a b c =∴设a=2k ,b=3k ,c=5k ,(1);(2)∵324a b c -+=∴6k-3k+5k=24,∴k=3,∴a=2×3=6,b=3×3=9,c=5×3=15.【点睛】本题考查了比例的性质的应用,主要考查学生的计算能力.12.ABC ∆中,正方形EFGH 的两个顶点E 、F 在BC 上,另两个顶点G 、H 分别在 AC 、AB 上,BC = 15,BC 边上的高AD = 10,求正方形EFGH 的面积.【难度】★★【答案】36.【解析】设正方形EFGH 的边长为a ,易知:.,.,, 6a ∴=,正方形EFGH 的面积为36.【总结】本题考查三角形内接正方形的模型,熟练掌握此题涉及的知识点.13.如图,直角梯形ABCD 中,AB // CD ,,点E 在边BC 上,且, AD = 10,求AED ∆的面积.【难度】★★【答案】24.【解析】90ABC ∠=,//AB CD ,.又, .. . ,. 90AED ∠=.在Rt AED ∆中, 10AD =,. 24AED S ∆∴=.【总结】本题考查一线三等角模型的相似问题,还有外角知识、平行的判定等.14.把两块全等的直角三角板ABC 和DEF 叠放在一起,使三角板DEF 的锐角顶点D与三角板ABC 的斜边中点O 重合,其中,45C F ∠=∠=︒,AB =DE = 4,把三角板ABC 固定不动,让三角板DEF 绕点O 旋转,设射线DE 与射线AB 相交于点P ,射线DF 与线段BC 相交于点Q .(1)如图1,当射线DF 经过点B ,即点Q 与点B 重合时,易证APD ∆∽,则此时AP CQ =______;(2)将三角板DEF 由图1所示的位置绕点O 沿逆时间方向旋转,设旋转角为α.其 中090α︒<<︒,问AP CQ 的值是否改变?请说明理由.【难度】★★【答案】(1)8;(2)不改变.【解析】(2)易证APD CDQ ∆∆∽, 得:AP AD CD CQ = AP CQ CD AD ∴•=•.又4AC = CD AD ∴== 8AP CQ ∴•=.【总结】本题考查旋转的相关知识,等腰三角形,“一线三等角”得相似等的相关知识.15.如图,已知平面直角坐标系中三点A (2,0),B (0,2),P (a ,0)(a < 0),联结BP ,过点P 作PC ⊥PB 交过点A 的直线l 于点C (2,b ).(1)求b 与a 之间的函数关系式;(2)当a 取得最大的整数时,求BC 与x 轴的交点Q 的坐标.【难度】★★【答案】(1)212b a a =-+;(2). 【解析】(1)即22a b a -=-- 212b a a =-+; (2)0a <a ∴取得最大的整数时1a =- 32b ∴=-//OB AC OB OQ AC QA∴=,即2322OQ OQ =- 87OQ ∴= . 【总结】本题考查相似的判定及性质等知识.。
专题08 角平分线的重要模型(二)非全等类角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,,本专题就角平分线的非全等类模型作相应的总结,需学生反复掌握。
模型1.双角平分线模型(导角模型) 【模型解读】双角平分线模型(导角模型)指的是当三角形的内角(外角)的平分线相交时,可以导出平分线的夹角的度数。
【模型图示】条件:BD ,CD 是角平分线.结论:1902BDC A∠=︒+∠1902BDC A ∠=︒-∠12BDC A ∠=∠ 1.(2022·广东·九年级专题练习)BP 是∠ABC 的平分线,CP 是∠ACB 的邻补角的平分线,∠ABP =20°,∠ACP =50°,则∠P =( )4231AFCB4321DAA.30°B.40°C.50°D.60°【答案】A【分析】据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠P 的度数.【详解】∠BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∠∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,∠∠PCM是△BCP的外角,∠∠P=∠PCM−∠CBP=50°−20°=30°,故选:A.【点睛】本题考查三角形外角性质以及角平分线的定义,解题时注意:一个三角形的外角等于与它不相邻的两个内角的和.2.(2022·山东·济南中考模拟)如图1,在△ABC中,∠BAC的平分线AD与∠BCA的平分线CE交于点O.∠ABC;(1)求证:∠AOC=90°+12(2)当∠ABC=90°时,且AO=3OD(如图2),判断线段AE,CD,AC之间的数量关系,并加以证明.∠MK=ML,角与第三个内角的数量关系”进行了探究.(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC=;(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC 与∠A的数量关系,并说明理由.(4)如图4,△ABC外角∠CBM、∠BCN的平分线交于点Q,∠A=64°,∠CBQ,∠BCQ的平分线交于点P,则∠BPC=°,延长BC至点E,∠ECQ的平分线与BP的延长线相交于点R,则∠R=°.【分析】(1)根据三角形的内角和角平分线的定义;(2)根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠E与∠1表示出∠2,于是得到结论;(3)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠EBC与∠ECB,然后再根据三角形的内角和定理列式整理即可得解;(4)结合(1)(2)(3)的解析即可求得.【解答】解:(1)∵PB、PC分别平分∠ABC和∠ACB,∴∠PBC=12∠ABC,∠PCB=12∠ACB(角平分线的性质),∴∠BPC+∠PBC+∠PCB=180°(三角形内角和定理),∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(12∠ABC+12∠ACB)=180°−12(∠ABC+∠ACB)=180°−12(180°﹣∠A)=180°﹣90°+12∠A=90°+12∠A=90°+12×64°=122°.故答案为:122°;(2)∵BE是∠ABD的平分线,CE是∠ACB的平分线,∴∠ECB=12∠ACB,∠ECD=12∠ABD.∵∠ABD是△ABC的外角,∠EBD是△BCE的外角,∴∠ABD=∠A+∠ACB,∠EBD=∠ECB+∠BEC,∴∠EBD=12∠ABD=12(∠A+∠ACB)=∠BEC+∠ECB,即12∠A+∠ECB=∠ECB+∠BEC,∴∠BEC=12∠A=12α;(3)结论∠BQC=90°−12∠A.∵∠CBM与∠BCN是△ABC的外角,∴∠CBM=∠A+∠ACB,∠BCN=∠A+∠ABC,∵BQ,CQ分别是∠ABC与∠ACB外角的平分线,∴∠QBC=12(∠A+∠ACB),∠QCB=12(∠A+∠ABC).∵∠QBC+∠QCB+∠BQC=180°,∴∠BQC=180°﹣∠QBC﹣∠EQB=180°−12(∠A+∠ACB)−12(∠A+∠ABC),=180°−12∠A−12(∠A+∠ABC+∠ACB)=180°−12∠A﹣90°=90°−12∠A;(4)由(3)可知,∠BQC=90°−12∠A=90°−12×64°=58°,由(1)可知∠BPC=90°+12∠BQC=90°+12×58°=119°;由(2)可知,∠R=12∠BQC=29°故答案为119,29.【点评】本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.4.(2022·辽宁沈阳·九年级期中)阅读下面的材料,并解决问题(1)已知在∠ABC中,∠A=60°,图1-3的∠ABC的内角平分线或外角平分线交于点O,请直接写出下列角度的度数,如图1,∠O=;如图2,∠O=;如图3,∠O=;∠A(2)如图4,点O是∠ABC的两条内角平分线的交点,求证:∠O=90°+12(3)如图5,在∠ABC中,∠ABC的三等分线分别与∠ACB的平分线交于点O1O2,若∠1=115°,∠2=135°,求∠A的度数.模型2.角平分线加平行线等腰现(角平分线+平行线)【模型解读】1)过角平分线上一点作角的一边的平行线,构造等腰三角形;2)有角平分线时,过角一边上的点作角平分线的平行线,交角的另一边的直线于一点,也可构造等腰三角形。
角平分线和平行线构成等腰三角形的探究-----李春蕊北京市育英学校一、教材分析:《等腰三角形》是“人教版八年级数学(上)”第十二章第三节的内容。
等腰三角形是一种特殊的三角形,它除了具备一般三角形的所有性质外,还有许多特殊的性质,由于这些特殊性质,使它比一般的三角形应用更广泛。
这一单元的主要内容是等腰三角形的性质和判定,以及等边三角形的相关知识,尤其是等腰三角形的性质和判定,它们是研究等边三角形、证明线段等和角等的重要依据.学情分析:本节课在学生已经学习了轴对称、等腰三角形性质及判定基础上,进一步探究角平分线和平行线形成等腰三角形的问题。
学生具有一定说理能力,整体几何感观比较清晰,在探究活动中,能够根据老师的问题进行有切入的思考。
二、教学目标:(1)掌握角平分线和平行线形成等腰三角形的基本规律;(2)体会研究问题中用到的分类思想,经历由特征图形问题的解决,发展对问题的进一步探究,认识到在几何问题中,位置关系可得出一定数量关系,特殊的数量关系也能推出一定位置关系.(3)通过交流和研讨,使学生在探索的同时获得解决问题的一种方法,提高学生学习数学的兴趣和信心.教学重点:掌握角平分线+平行线能形成等腰三角形这个基本规律,利用这个规律解决等腰三角形方面的有关问题.教学难点:灵活运用角平分线和平行线形成等腰三角形这个基本规律解决有关问题.突出重点方法:观察,思考,证明.突出难点方法:自主探究教学方法:启发与探究相结合教学准备:PPT,课本,作图工具三、教学设计:(一)复习等腰三角形相关知识1、请同学们对等腰三角形的知识要点进行自我回顾:(由学生先进行回顾,教师补充)(二)探究过程问题1:已知∠ABC,BD平分∠ABC,ED//BC.思考:△EBD是等腰三角形吗?解:是;EB=ED发现:无论点D 在BD 上如何运动,△EBD 都是等腰三角形结论:角平分线+平行线 等腰三角形我们在几何证明中,一般不单独研究角,大多数都是借助图形,比如在三角形中研究问题,上面问题如果放在三角形中,我们可以作三角形中一个角的角平分线,然后过角平分线上一点,作这个角的一边的平行线。
平行线及角平分线类相似中考要求重难点1.相似定义,性质,判定,应用和位似2.相似的判定和证明3.相似比的转化课前预习上一节课我们知道了相似三角形的由来,那你是否知道其他跟金子塔有关的不可思议的事实呢?不仅建造金字搭的技术中,表现了古埃及人的非凡的数学天才;而且,它本身的许多数据,也说明了古埃及人的数学才华,巧夺天工,比如,胡夫金字塔底面周长365米,恰好是一年的天娄;周长乘以2,正是赤道的时分度;搭高乘以10九次方,正是地球到太阳的距离;周长除以塔塔高的2倍,正是圆周率3.1415926……;塔的自重乘以10的15次方,正好是地球的重量;塔里放置的棺材內部尺寸,正好是几千年后希腊数学家华连哥拉斯发现华连哥拉斯数——345∶∶.数学的趣味是无法言语的,同学们可以从身边的点滴去发现其中的奥秘.例题精讲模块一 平行线类相似问题平行线类相似的基本模型有☞模型一、二类综合题【例1】 如图,在ABC △中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BCCD=____ ___. MECBA【难度】3星【解析】先介绍常规的解法:BCFE DMA BCFED M A如图,过点C 作DE 或AB 的平行线均可,不妨以左图为例来说明. 过点C 作//CF DE ,交AB 于点F . ∵AM MC =,//CF DE ∴AE EF = ∵14AE AB =∴2BF EF= ∵//CF DE ∴2BC BFCD EF== 当然,过点M 、点E 作适当的平行线,均可作出此题,这里不再给出.以上这些解法均属于常规解法,下面介绍特殊的解法: 看ABC ∆为直线EM D 所截,由梅涅劳斯定理可知,1AE BD CM EB DC MA⋅⋅= 又14AE AB =,AM CM =,故32BD BC DC CD=⇒= 上述图形是一个经典的梅氏定理的基本图形,解类似的题时,梅氏定理的运用能够带来立竿见影的效果,很快得出答案,梅氏定理的证明见变式1,先讲变式1再介绍本解法.【答案】2【巩固】如图,AD 是ABC △的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.AB CDEF【难度】3星【解析】1()过点D 、E 、F 作平行线均可构造出平行线的基本图形,然后利用 这些基本图形的性质来解题.以下给出6种辅助线(还有几种没给 出),解题过程不再给出.HAB C DEF ABCD EF HHAB CDEFHAB CD EFHAB CDEFHABCD EF当然,本题也可由梅氏定理直接得出结果. 看ADC ∆被直线BEF 所截,由梅氏定理可得1AF CB DEFC BD EA⋅⋅= 又AE DE =,BD CD =,故12AF FC =. 2()结论依然成立,解法同上(包括用梅氏来解题),不再给出. 【答案】1()见解析;2()结论依然成立【拓展】如图,在ABC △中,D 为BC 边的中点,E 为AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD 的值; (2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想. E DBACO【难度】4星 【题型】解答 【解析】1()当11211AE EC ==+时,22321AO AD ==+; 2()当11A 312AE C ==+时,21222AO AD ==+;当1A 4AE C =时,22532AO AD ==+.3()当1A 1AE C n =+时,22AO AD n=+,证明方法比较多,选择两种介绍:如上右图,过点D 作//DF BE ,交AC 于点F . ∵//DF BE ,BD CD = ∴EF CF = ∵11AE AC n =+ ∴CE nAE =,122nEF CE AE == ∵//DF BE ∴222AO AE AO OD EF n AD n==⇒=+ OFCABDE另一种解法就是梅氏定理,看ADC ∆被直线BOE 所截可知1AO DB CE OD BC EA ⋅⋅=,而11AE CE nAE AC n =⇒=+,BD CD =,故22AO AD n=+. 【答案】1()23AO AD =;2()当1A 3AE C =时,12AO AD =;当1A 4AE C =时,25AO AD =3()当1A 1AE C n =+时,22AO AD n =+【例2】 如图,在四边形ABCD 中,AC 与BD 相交于点O ,直线l 平行于BD ,且与AB 、DC 、BC 、AD及AC 的延长线分别相交于点M 、N 、R 、S 和P .求证:PM PN PR PS ⋅=⋅lSR PNMODC BA【难度】5星 【解析】略【答案】∵BO OC ODBD MS PR CP PN⇒==∥ ∴PN ODPR BO=∵BO AO ODBD MS PM AP PS⇒==∥∴PS ODPM BO=∴PN PSPM PN PR PS PR PM=⇒⋅=⋅ 点评:本题通过证明原结论的变形式——两个分式(比例)等于一个相同(或相等)的分式(比例)来证明他们【巩固】已知,如图,四边形ABCD ,两组对边延长后交于E 、F ,对角线BD EF ∥,AC 的延长线交EF于G .求证:EG GF =.【难度】5星G F ECDBANM G FECD B A【解析】略 【答案】证法一:过C 作MN EF ∥交AE 、AF 于M N ,, 则有MC EM FN CNBD EB FD BD===, ∴MC CN =, 又∵MN EF ∥, ∴MC AC CNEG AG GF==, ∴EG GF =.证法二:由塞瓦定理的充分性可得:1EG FD AB GF DA BE ⋅⋅=.又因为AB ADBE DF=,代入上式得1EG FD AD GF DA DF ⋅⋅=,即1EGGF=.所以EG GF =.【巩固】已知:P 为ABC ∆的中位线MN 上任意一点,BP 、CP 的延长线分别交对边AC 、AB 于D 、E ,求证:1AD AEDC EB+=PNME D CBA RQPNME D CBA【难度】5星 【解析】略【答案】延长BD 、CE 分别交过A 的平行BC 的直线于R 、Q 两点,∵QR MN BC ∥∥,且AM BM =, ∴PQ PC =,PR PB =又∵QPR CPB ∠=∠∴PQR PCB ∆∆≌,可得QR BC =, 又∵AD AR DC BC =,AE AQEB BC=, ∴1AD AE AR AQ AR AQ RQ BC CD EB BC BC BC BC BC++=+====☞模型三类综合题【例3】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.DCF EB A【难度】4星 【解析】略【答案】∵//AB EF ∴EF DFAB BD =∵//CD EF ∴EF BFCD BD=两式相加并变形可得,111EF AB CD =+,即111c a b=+.【巩固】如上图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FDCEAB【难度】4星 【解析】略【答案】由AB BD ⊥,CD BD ⊥,EF BD ⊥,则必有////AB CD EF .进而可知EF DF AB BD =,EF BFCD BD=,两式相加并变形可得,111EF AB CD =+【巩固】如图,已知////AB EF CD ,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.NM H D CF EB A【难度】4星 【解析】略 【答案】111BEDABDBCDS S S ∆∆∆=+,过点A 、E 、C 分别作BD 的垂线,垂足为H 、M 、N .由变式1可知,111EM AH CN =+,故 111111222BD EM BD AH BD CN =+⋅⋅⋅即111BEDABDBCDS S S ∆∆∆=+点评:此题的证明过程体现了“集中”这一思想,将EF AB 、EFCD集中到同一条线段BD 上,从而发现它们的和是一个常数.【拓展】如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA【解析】:方法一:由AD BC ∥可知,1212aEP AE a EP a PQ abPQ PB BF b EB a b BC a bb ===⇒==⇒=++ 方法二:观察此题与上题颇为相似,于是猜想////PQ AB CD ,但是本题中没有可以直接使用基本 图形结论的条件,可通过连接EF 来实现,设EF 、PQ 交于点O . ∵//AD BC ∴AP AE PF BF=,DQ DE FQ CF = ∵AE DE =,BF CF = ∴////AP DQ PQ AD BC PF FQ=⇒ ∴OP OF OQ OP OQ AE EF DE ==⇒=(∵AE DE =,其中OFEF为中间过渡量) ∵////AE OP BF ∴111222()abOP OP AE BF a b a b =+=+⇒=+ ∴abPQ a b=+ 如果双向延长PQ 分别与AB 、CD 交于点G 、H ,则有GP OP OQ QH ===.模块二 角平分线类相似问题角平分线类的相似模型如下:方法点播:角平分线类得相似问题基本就这样的两种模型,辅助线的做法也如图中虚线所示,学生在学这部分知识时,不管是平时测验和期中、期末考试,只要涉及到角平分线和证明相似问题就可以试着做这样的辅助线,基本都可以解决.【例4】 在Rt ABC △中,线段CE 平分ACB ∠交AB 于点E ,交斜边上的高AD 于点O ,过O 引BC 的平行线交于F .求证:AE BF =.321OF E DCBA【难度】3星【解析】在相似问题中遇到证明线段相等的问题时一定要能想到:这个证明可能是由两组成比例线段进行等量代换得到.本题由角平分线得到角相等再由都是直角三角形,可证明一组相似三角形得到一组成比例线段CD AC OD AE =,再根据平行线分三角形两边成比例得到比例线段ADABOD BF =,最后再根据一组相似三角形得到成比例线段AD AB CD AC =,等量代换得到ODBFOD AE =,题目得证AE BF =.【答案】∵CE 平分ACB ∠∴23∠=∠∴Rt CAE Rt CDO △∽△ ∴CDACOD AE =又∵OF BC ∥ ∴ADABOD BF = 又∵Rt ABD Rt CAD △∽△ ∴AD AB CD AC =,即ODBFOD AE =∴AE BF =注意:应用比例线段证明两直线平行或两线段相等时,(1)要注意如果相关的比例式较多,一时难以作出选择,应将所有相关的比例式都写出来,然后再仔细对比、分析选出有用的。