相似三角形-构造相似辅助线双垂直模型

相似三角形难题精选模块一：相似三角形中的动点问题如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB1∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB1于F，G是EF中点，连接DG．设点D运动的时间为t秒．（1）当t为何值时，AD=AB，并求出此时DE的长度；（2）当△DEG与△ACB相似时，求t的值．如图，在△ABC中，ABC＝90°，AB=6m，BC=8m，动点P以2m/s的速度从A点出发，沿AC 向点C移动．同时，动点Q以1m/s的速度从C点出发，沿CB向点B移动．当其中有一点到达终点时，它们都停止移动．设移动的时间为t秒．（1）①当t=2.5s时，求△CPQ的面积；②求△CPQ的面积S（平方米）关于时间t（秒）的函数解析式；（2）在P，Q移动的过程中，当△CPQ为等腰三角形时，求出t的值．如图1，在Rt△ABC中，ACB＝90°，AC＝6，BC＝8，点D在边AB上运动，DE平分CDB交边BC于点E，EM⊥BD，垂足为M，EN⊥CD，垂足为N．（1）当AD＝CD时，求证：DE∥AC；（2）探究：AD为何值时，△BME与△CNE相似？如图所示，在△ABC中，BA＝BC＝20cm，AC＝30cm，点P从A点出发，沿着AB以每秒4cm 的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，当P点到达B点时，Q点随之停止运动．设运动的时间为x．（1）当x为何值时，PQ∥BC？（2）△APQ与△CQB能否相似？若能，求出AP的长；若不能，请说明理由.如图，在矩形ABCD中，AB=12cm，BC=6cm，点P沿AB边从A开始向点B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（s）表示移动的时间（0＜t＜6）。

相似三角形优秀教案相似三角形教案相似三角形教案(好)一、知识概述(一)相似三角形1、对应角相等，对应边成比例的两个三角形，叫做相似三角形．温馨提示：①当且仅当一个三角形的三个角与另一个(或几个)三角形的三个角对应相等，且三条对应边的比相等时，这两个(或几个)三角形叫做相似三角形，即定义中的两个条件，缺一不可；②相似三角形的特征：形状一样，但大小不一定相等；③相似三角形的定义，可得相似三角形的基本性质：对应角相等，对应边成比例，其应用广泛．2、相似三角形对应边的比叫做相似比．温馨提示：①全等三角形一定是相似三角形，其相似比k=1．所以全等三角形是相似三角形的特例．其区别在于全等要求对应边相等，而相似要求对应边成比例．②相似比具有顺序性．例如△ABC∽△A′B′C′的对应边的比，即相似比为k，则△A′B′C′∽△ABC的相似比，当且仅当它们全等时，才有k=k′=1．③相似比是一个重要概念，后继学习时出现的频率较高，其实质它是将一个图形放大或缩小的倍数，这一点借助相似三角形可观察得出．3、如果两个边数相同的多边形的对应角相等，对应边成比例，那么这两个多边形叫做相似多边形．4、相似三角形的预备定理：如果一条直线平行于三角形的一条边，且这条直线与原三角形的两条边(或其延长线)分别相交，那么所构成的三角形与原三角形相似．温馨提示：①定理的基本图形有三种情况，如图其符号语言：∵DE∥BC，∴△ABC∽△ADE；②这个定理是用相似三角形定义推导出来的三角形相似的判定定理．它不但本身有着广泛的应用，同时也是证明下节相似三角形三个判定定理的基础，故把它称为“预备定理”；③有了预备定理后，在解题时不但要想到上一节“见平行，想比例”，还要想到“见平行，想相似”．(二)相似三角形的判定1、相似三角形的判定：判定定理(1)：两角对应相等，两三角形相似．判定定理(2)：两边对应成比例且夹角相等，两三角形相似．判定定理(3)：三边对应成比例，两三角形相似．温馨提示：①有平行线时，用上节学习的预备定理；②已有一对对应角相等(包括隐含的公共角或对顶角)时，可考虑利用判定定理1或判定定理2；③已有两边对应成比例时，可考虑利用判定定理2或判定定理3．但是，在选择利用判定定理2时，一对对应角相等必须是成比例两边的夹角对应相等．2、直角三角形相似的判定：斜边和一条直角边对应成比例，两直角三角形相似．温馨提示：①由于直角三角形有一个角为直角，因此，在判定两个直角三角形相似时，只需再找一对对应角相等，用判定定理1，或两条直角边对应成比例，用判定定理2，一般不用判定定理3判定两个直角三角形相似；②如图是一个十分重要的相似三角形的基本图形，图中的三角形，可称为“母子相似三角形”，其应用较为广泛．③如图，可简单记为：在Rt△ABC中，CD⊥AB，则△ABC∽△CBD∽△ACD．(三)三角形的重心1、三角形三条中线的交点叫做三角形的重心．2、三角形的重心与顶点的距离等于它与对边中点的距离的两倍．二、重点难点疑点突破1、寻找相似三角形对应元素的方法与技巧正确寻找相似三角形的对应元素是分析与解决相似三角形问题的一项基本功．通常有以下几种方法：(1)相似三角形有公共角或对顶角时，公共角或对顶角是最明显的对应角；相似三角形中最大的角(或最小的角)一定是对应角；相似三角形中，一对相等的角是对应角，对应角所对的边是对应边，对应角的夹边是对应边；(2)相似三角形中，一对最长的边(或最短的边)一定是对应边；对应边所对的角是对应角；对应边所夹的角是对应角．2、常见的相似三角形的基本图形：学习三角形相似的判定，要与三角形全等的判定相比较，把证明三角形全等的思想方法迁移到相似三角形中来；对一些出现频率较高的图形，要善于归纳和记忆；对相似三角形的判定思路要善于，形成一整套完整的判定方法．如：(1)“平行线型”相似三角形，基本图形见上节图．“见平行，想相似”是解这类题的基本思路；(2)“相交线型”相似三角形，如上图．其中各图中都有一个公共角或对顶角．“见一对等角，找另一对等角或夹等角的两边成比例”是解这类题的基本思路；(3)“旋转型”相似三角形，如图．若图中∠1=∠2，∠B=∠D(或∠C=∠E)，则△ADE∽△ABC，该图可看成把第一个图中的△ADE绕点A旋转某一角度而形成的．温馨提示：从基本图形入手能较顺利地找到解决问题的思路和方法，能帮助我们尽快地找到添加的辅助线．以上“平行线型”是常见的，这类相似三角形的对应元素有较明显的顺序，“相交线型”识图较困难，解题时要注意从复杂图形中分解或添加辅助线构造出基本图形．三、解题方法技巧点拨1、寻找相似三角形的个数例1、(吉林)将两块完全相同的等腰直角三角形摆成如图的样子，假设图形中所有点、线都在同一平面内，回答下列问题：(1)图中共有多少个三角形？把它们一一写出来；(2)图中有相似(不包括全等)三角形吗？如果有，就把它们一一写出来．分析：(1)在△ABC内，有五个三角形，加上△ABC与△AFG，共有七个三角形．(2)这是依据相似三角形判定定理来解决的计数问题．由于“不包括全等”，图中还剩五个非直角三角形，考虑到题设中两个三角形摆放的随意性，∠1不一定等于∠2，而∠B=∠C=45°，∠3、∠4都为钝角，又排除△ABD与△ACE相似，还剩三个三角形，这三个三角形相似．解：(1)共有七个三角形，它们是△ABD、△ABE、△ADE、△ADC、△AEC、△ABC与△AFG．(2)有相似三角形，它们是△ABE∽△DAE，△DAE∽△DCA，△ABE∽△DCA(或△ABE∽△DAE∽△DCA)．点拨：①解决这类计数问题，一定要依据图形与定理，全面、周密思考，做到不重不漏，这类题有利于发散思维的培养和创新意识的形成；②有兴趣的同学可继续探索一下本题中BD、DE、EC三条线段有何关系？2、画符合要求的相似三角形例2、(上海)在大小为4×4的正方形方格中，△ABC的顶点A、B、C在单位正方形的顶点上，请在图中画出一个△A1B1C1，使得△A1B1C1∽△ABC(相似比不为1)，且点A1、B1、C1都在单位正方形的顶点上．（1）（2）分析：设单位正方形的边长为1，则△ABC的三边为，从而根据相似三角形判定定理2或3可画△A1B1C1，易得点拨：在4×4的正方形方格中，满足题设的△A1B1C1只能画出以上三个，若正方形方格数不加限制，则和△ABC相似且不全等的三角形可以画无数个．3、相似三角形的判定例3、(1)如图，O是△ABC内任一点，D、E、F分别是OA、OB、OC的中点，求证：△DEF∽△ABC；(2)如图，正方形ABCD中，E是BC的中点，DF=3CF，写出图中所有相似三角形，并证明．分析：(1)根据题设，观察图形易见，DE、EF、FD分别是△AOB、△BOC、△COA的中位线，利用三角形的中位线性质可证△DEF与△ABC的三边对应成比例；(2)由于正方形的四条边相等，且BE=CE，DF=3CF，设出正方形边长后，图中所有线段都能求出，故可从三边是否成比例判定哪些三角形相似．点拨：①第(1)题，若点O在△ABC外，其他条件不变，结论仍成立；②第(2)题也可用判定定理2，先证△ABE∽△ECF，得出∠AEF=90°后，再证其中任意三角形与△AEF相似，显然，以上证法较简便．4、直角三角形相似的判定例4、求证：若一个直角三角形的一条直角边和斜边上的高与另一个直角三角形的一条直角边和斜边上的高成比例，那么这两个直角三角形相似．已知：如图，Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，CD、C′D′分别是两个三角形斜边上的高，且CD︰C′D′=AC︰A′C′．求证：△ABC∽△A′B′C′．分析：判定直角三角形相似的方法除使用一般三角形的判定方法外，还可使用“斜边和一直角边对应成比例的两直角三角形相似”这一定理．证明△ABC∽△A′B′C′，只要再证一锐角对应相等即可．证明：∵CD、C′D′分别是△ABC、△A′B′C′的高，∴△ACD、△A′C′D′是直角三角形．5、三角形重心问题例5、已知△ABC的重心G到BC边上的距离为5，那么BC边上的高为()A．5 B．12C．10 D．15解析：因为G为△ABC的重心，所以DG︰DA=1︰3，因为GE⊥BC，AF⊥BC，所以GE∥AF，所以GE︰AF=DG︰DA=1︰3，因为GE=5，所以AF=15．6、相似三角形的综合运用例6、如图，CD是Rt△ABC斜边AB上的中线，过点D垂直于AB的直线交BC于E，交AC延长线于F．求证：(1)△ADF∽△EDB；(2)CD2=DE·DF．分析：(1)△ADF与△EDB都是直角三角形，要证它们相似，只要再找一个角对应相等即可；(2)注意到CD是斜边AB的中线，AD=BD=CD，由结论(1)不难得出结论(2)．证明：(1)∵DF⊥AB，∴∠ADF=∠BDE=90°，又∵∠F＋∠A=∠B＋∠A，∴∠F=∠B，∴△ADF∽△EDB．(2)由(1)得，∴AD·BD=DE·DF．又∵CD是Rt△ABC斜边上的中线，∴AD=BD=CD．故CD2=DE·DF．点拨：本题综合考查了直角三角形的性质与相似三角形的判定等．这是一道阶梯型问题，第(2)题根据(1)得出有关比例式，然后使用“等线代换”使问题简捷获证．其实第(2)题也可这样思考：把它转化为比例式，证明这三条线段所在的△CDE∽△FDC．请同学们完成这一证明．例7、如图，AD是△ABC的角平分线，BE⊥AD于E，CF⊥AD于F．求证：．分析：待证式中的四条线段不是在两个三角形中，无法直接根据两个三角形相似得出，需要插入一个“中间比”，由题设易证△ABE∽△ACF，△BDE∽△CDF，从中不难找到这个中间比．证明：∵AD是△ABC的角平分线，∴∠1=∠2．∵BE⊥AD，CF⊥AD，∴∠3=∠4=90°，∴△ABE∽△ACF，点拨：①当无法直接由两个三角形相似得出结论中的比例式时，一般可寻找“中间比”帮忙；例8、如图，在正方形ABCD中，M、N分别是AB、BC上的点，BM=BN，BP⊥MC于点P．求证：(1)△PBN∽△PCD；(2)PN⊥PD．分析：要证PN⊥PD，即证∠DPN=90°，由已知∠BPC=90°，而∠BPC与∠DPN有公共部分∠CPN，因此只要证明∠4=∠5即可．这就必须先证明出结论(1)．在△PBN与△PCD中，易证∠1=∠3，以下只要证明夹∠1、∠3的两边对应成比例．证明：(1)在正方形ABCD中，AB∥CD，∠ABC=90°．∵BP⊥MC，∴△PBM∽△PCB．点拨：要注意观察出图中存在的“母子相似三角形”基本图形，从而充分利用它得出∠1=∠2及△PBM∽△PCB等重要结论相似三角形教案相似三角形教案①回忆两个三角形相似的概念，巩固两个三角形相似的性质与判定。

专题06相似三角形的基本模型（子母型）
【模型说明】
“母子”模型的图形（通常有一个公共顶点和另外一个不是公共的顶点，由于小三角形寓于大三角形中，恰似子依母怀），也是有一个“公共角”，再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似．
图1图2图3 1）“母子”模型（斜射影模型）
条件：如图1，∠C=∠ABD；结论：△ABD∽△ACB，AB2＝AD·AC.
2）双垂直模型（射影模型）
条件:如图2，∠ACB=90o，CD⊥AB；
结论：△ACD∽△ABC∽△CBD；CA2＝AD·AB，BC2＝BD·BA，CD2＝DA·DB.
3）“母子”模型（变形）
条件:如图3，∠D=∠CAE，AB=AC；结论：△ABD∽△ECA；
【例题精讲】
（1）求直线AB 的解析式及抛物线顶点坐标；
（2）如图1，点P 为第四象限且在对称轴右侧抛物线上一动点，过点为C ，PC 交AB 于点D ，求PD BD +的最大值，并求出此时点（3）如图2，将抛物线215:324
L y x x =--向右平移得到抛物线于M ，N 两点，若点A 是线段MN 的中点，求抛物线L '的解析式．
课后训练
4．如图，在矩形ABCD中，＝45°，则DF的长是。

双垂直、三垂直模型例题讲解：例1、如图，在△ABC和△CDE中，∠B=∠D=90°，C为线段BD上一点，且AC⊥CE，求证：AB.DE=BC.CD例2、如图，在△ABC中，∠C=90°，∠B=60°，D是AC上一点，DE⊥AB于E，且CD=2，DE=1，则BC的长为（）A、2B、433C、23D、43例3、（射影定理）如图，已知BA⊥AD，AC⊥BD，求证：①AC2=BC.CD②AB2=BC.BD③AD2=CD.BD④AB.AD=AC.BD课堂练习1、如图，在Rt△ABC中，∠ACB=90°，BC=3，AC=4，AB的垂直平分线DE交BC的延长线于点E，则CE的长为（）A、32B、76C、256D、22、如图，矩形ABCD中，AB=3，BC=5。

过对角线交点O作OE⊥AC交AD于E，则AE的长是（）A、1.6B、2.5C、3D、3.43、如图，在Rt△ABC中，AD⊥BC于D，DE⊥AB于E，若AD=3，DE=2，则AC=（）A、212B、152C、15D、924、如图，△ABC中，∠B=90°，AB=6，BC=8，将△ABC沿DE折叠，使点C落在AB边上的C’处，并且C’D//BC，则CD的长是（）A、409B、509C、154D、2545、如图，将矩形纸片ABCD沿EF折叠，使点B与CD的中点B’重合，若AB=2，BC=3，则△ECB’与△B’DG的面积之比为（）A、9:4B、3:2C、4:3D、16:96、如图，四边形ABCD和四边形ACED都是平行四边形，点R为DE的中点，BR分别交AC、CD于点P、O。

则CP：AC等于（）A、1:3B、1:4C、2:3D、3:47、如图，在△ABC中，AB=AC，BD=CD，CE⊥AB于E。

求证：△ABD∽△CBE8、如图，CD、BE分别是锐角△ABC中AB、AC边上的高线，垂足为D、E （1）证明：AD.EB=AE.DC（2）若∠A=60°，求S△AED：S△ABC例3、（三等角模型）如图，等腰直角△ABC的直角边长为3，P为斜边BC上一点，且BP=1，D为AC上一点，若∠APD=45°，则CD的长为（）A、53-B、2313-C、3213D、35例4、如图，已知等边△ABC中，D、E两点在直线BC上，且∠DAE=120°（1）判断△ABD是否与△ECA相似，并说明你的理由（2）当CE.BD=16，求△ABC的周长10、如图，在△ABC中，∠B=∠AEM=∠C，且点A在DE上，点E在BC上，EF与AC交于点M。

相似三角形重要模型之(双)A字型与(双)8字型相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考的常考题型。

本专题重点讲解相似三角形的(双)A字模型和(双)8(X)字模型．A字型和8(X)字型的应用难点在于过分割点(将线段分割的点)作平行线构造模型，有的是直接作平行线，有的是间接作平行线(倍长中线就可以理解为一种间接作平行线)，这一点在模考中无论小题还是大题都是屡见不鲜的。

模型1. “A”字模型【模型解读与图示】“A”字模型图形(通常只有一个公共顶点)的两个三角形有一个“公共角”(是对应角)，再有一个角相等或夹这个公共角的两边对应成比例，就可以判定这两个三角形相似．图1 图2 图31)“A”字模型条件：如图1，DE∥BC；结论：△ADE∽△ABC⇔ADAB =AEAC=DEBC.2)反“A”字模型条件：如图2，∠AE D=∠B；结论：△ADE∽△ACB⇔ADAC =AEAB=DEBC.3)同向双“A”字模型条件：如图3，EF∥BC；结论：△AEF∽△ABC，△AEG∽△ABD，△AGF∽△ADC⇔EGBD=FGCD=AGAD1(2023·湖北十堰·统考中考真题)如图，在菱形ABCD中，点E，F，G，H分别是AB，BC，CD，AD上的点，且BE=BF=CG=AH，若菱形的面积等于24，BD=8，则EF+GH=．2(2023·安徽·九年级期末)如图，在三角形△ABC中，点D、E分别在边AB、AC上，AD=3，BD=1，AE =2，EC=4．(1)求证：∠ADE=∠C；(2)若∠BAC的平分线交DE于点F，交BC于点G，求AFFG．3(2022·山东东营·中考真题)如图，在△ABC 中，点F 、G 在BC 上，点E 、H 分别在AB 、AC 上，四边形EFGH 是矩形，EH =2EF ,AD 是△ABC 的高．BC =8,AD =6，那么EH 的长为．4(2022·浙江宁波·中考真题)(1)如图1，在△ABC 中，D ，E ，F 分别为AB ,AC ,BC 上的点，DE ∥BC ,BF =CF ,AF 交DE 于点G ，求证：DG =EG ．(2)如图2，在(1)的条件下，连接CD ,CG ．若CG ⊥DE ,CD =6,AE =3，求DEBC的值．(3)如图3，在▱ABCD 中，∠ADC =45°,AC 与BD 交于点O ，E 为AO 上一点，EG ∥BD 交AD 于点G ，EF ⊥EG 交BC 于点F ．若∠EGF =40°,FG 平分∠EFC ,FG =10，求BF 的长．5(2023•安庆一模)如图，在△ABC 中，点D 、E 、F 分别在边BC 、AB 、CA 上，且DE ∥CA ，DF ∥AB ．(1)若点D 是边BC 的中点，且BE =CF ，求证：DE =DF ；(2)若AD ⊥BC 于D ，且BD =CD ，求证：四边形AEDF 是菱形；(3)若AE =AF =1，求1AB +1AC的值．模型2.“X ”字模型(“8”模型)【模型解读与图示】“8”字模型图形的两个三角形有“对顶角”，再有一个角相等或夹对顶角的两边对应成比例就可以判定这两个三角形相似．图1图2图3图41)“8”字模型条件：如图1，AB ∥CD ；结论：△AOB ∽△COD ⇔AB CD =OA OC =OBOD .2)反“8”字模型条件：如图2，∠A =∠D ；结论：△AOB ∽△DOC ⇔AB CD =OA OD =OBOC.3)平行双“8”字模型条件：如图3，AB ∥CD ；结论：AE DF =BE CF =ABCD4)斜双“8”字模型条件：如图4，∠1=∠2；结论：△AOD ∽△BOC ，△AOB ∽△DOC ⇔∠3=∠4.1(2022·辽宁·中考真题)如图，在正方形ABCD 中，E 为AD 的中点，连接BE 交AC 于点F ．若AB =6，则△AEF 的面积为．2(2023·黑龙江·哈尔滨九年级阶段练习)如图，AB ∥CD ,AE ∥FD ，AE ，FD 分别交BC 于点G ，H ，则下列结论中错误的是()A.DH FH =CHBHB.GE DF =CGCBC.AF CE =HGCGD.FH AG =BFFA3(2021·上海·中考真题)如图，在梯形ABCD 中，AD ⎳BC ,∠ABC =90°,AD =CD ,O 是对角线AC 的中点，联结BO 并延长交边CD 或边AD 于E ．(1)当点E 在边CD 上时，①求证：△DAC ∽△OBC ；②若BE ⊥CD ，求ADBC的值；(2)若DE =2,OE =3，求CD 的长．4(2022·贵州铜仁·中考真题)如图，在四边形ABCD 中，对角线AC 与BD 相交于点O ，记△COD 的面积为S 1，△AOB 的面积为S 2．(1)问题解决：如图①，若AB ⎳CD ，求证：S 1S 2=OC ⋅ODOA ⋅OB(2)探索推广：如图②，若AB 与CD 不平行，(1)中的结论是否成立？若成立，请证明；若不成立，请说明理由．(3)拓展应用：如图③，在OA 上取一点E ，使OE =OC ，过点E 作EF ∥CD 交OD 于点F ，点H 为AB的中点，OH 交EF 于点G ，且OG =2GH ，若OE OA=56，求S 1S 2值．模型3. “AX ”字模型(“A 8”模型)【模型解读与图示】图1图2图3 1)一“A”一“8”模型条件：如图1，DE∥BC；结论：△ADE∽△ABC，△DEF∽△CBF⇔ADAB=AEAC=DEBC=DFFC=FEBF2)两“A”一“8”模型条件：如图2，DE∥AF∥BC；结论：1BC +1DE=1AF.3)四“A”一“8”模型条件：如图3，DE∥AF∥BC,1BC+1DE=1AF=1AG；结论：AF=AG1(2022·山东东营·中考真题)如图，点D为△ABC边AB上任一点，DE∥BC交AC于点E，连接BE、CD 相交于点F，则下列等式中不成立的是()A.ADDB =AEECB.DEBC=DFFCC.DEBC=AEECD.EFBF=AEAC2(2021·江苏南京·中考真题)如图，AC与BD交于点O，OA=OD,∠ABO=∠DCO，E为BC延长线上一点，过点E作EF⎳CD，交BD的延长线于点F．(1)求证△AOB≌△DOC；(2)若AB=2,BC=3,CE=1，求EF的长．3(2022·重庆九年级期中)如图，AD与BC相交于点E，点F在BD上，且AB∥EF∥CD，求证：1AB +1CD=1EF.证明：∵AB∥EF，∴△DEF∽△DAB，∴EFAB=DFDB.又∵EF∥CD，∴△BEF∽△BCD.∴EFCD=BFBD.∴EF AB +EFCD=DFDB+BFBD=BDBD=1.∴1AB+1CD=1EF.4(2022•安庆模拟)在四边形ABCD中，对角线AC、BD相交于点O．(1)如图①，若四边形ABCD为矩形，过点O作OE⊥BC，求证：OE=12CD．(2)如图②，若AB∥CD，过点O作EF∥AB分别交BC、AD于点E、F．求证：EFAB =EFCD=2．(3)如图③，若OC平分∠AOB，D、E分别为OA、OB上的点，DE交OC于点M，作MN∥OB交OA于一点N，若OD=8，OE=6，直接写出线段MN长度．课后专项训练1(2021·山东淄博·中考真题)如图，AB,CD相交于点E，且AC⎳EF⎳DB，点C,F,B在同一条直线上．已知AC=P,EF=r,DB=q，则p,q,r之间满足的数量关系式是()A.1r +1q=1pB.1p+1r=2qC.1p+1q=1rD.1q+1r=2p2(2023秋·山西阳泉·九年级统考期末)如图，在四边形ABCD中，AB=AC，对角线AC与BD相交于点E，DE=3BE，AC⊥AD，∠ACB=75°，AE=33，则对角线AC与BD的长分别是()A.AC=43，BD=123B.AC=9，BD=419C.AC=6，BD=83D.AC=8，BD=4193(2023·福建福州·校考二模)在数学综合实践课上，某学习小组计划制作一个款式如图所示的风筝．在骨架设计中，两条侧翼的长度设计AB=AC=50cm，风筝顶角∠BAC的度数为110°，在AB，AC上取D，E 两处，使得AD=AE，并作一条骨架AF⊥DE．在制作风筝面时，需覆盖整个骨架，根据以上数据，B，C两点间的距离大约是( )(参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.43)A.41cmB.57cmC.82cmD.143cm4(2022·湖北十堰·中考真题)如图，某零件的外径为10cm，用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB．如果OA：OC=OB：OD=3，且量得CD=3cm，则零件的厚度x为()A.0.3cmB.0.5cmC.0.7cmD.1cm5(2022·湖南怀化·中考真题)如图，△ABC中，点D、E分别是AB、AC的中点，若S△ADE=2，则S△ABC=．6(2023·广东梅州·九年级统考期末)如图，在△ABC中，点F、G在BC上，点E、H分别在AB、AC上，四边形EFGH是矩形，EH=2EF，AD是△ABC的高，BC=15，AD=5，那么EH的长为．7(2023·广东深圳·校考三模)如图，在Rt△ABC中，∠ACB=90°，AC=BC=6，D是AB上一点，点E 在BC上，连接CD，AE交于点F，若∠CFE=45°，BD=2AD，则CE=．8(2022·四川宜宾·中考真题)如图，△ABC中，点E、F分别在边AB、AC上，∠1=∠2．若BC=4，AF =2，CF=3，则EF=．9(2022·辽宁阜新·中考真题)如图，在矩形ABCD中，E是AD边上一点，且AE=2DE，BD与CE相交于点F，若△DEF的面积是3，则△BCF的面积是．10(2022·湖北荆门·中考真题)如图，点G 为△ABC 的重心，D ，E ，F 分别为BC ，CA ，AB 的中点，具有性质：AG ：GD =BG ：GE =CG ：GF =2：1．已知△AFG 的面积为3，则△ABC 的面积为．11(2023·福建·统考中考真题)阅读下列材料，回答问题任务：测量一个扁平状的小水池的最大宽度，该水池东西走向的最大宽度AB 远大于南北走向的最大宽度，如图1．工具：一把皮尺(测量长度略小于AB )和一台测角仪，如图2．皮尺的功能是直接测量任意可到达的两点间的距离(这两点间的距离不大于皮尺的测量长度)；测角仪的功能是测量角的大小，即在任一点O 处，对其视线可及的P ，Q 两点，可测得∠POQ 的大小，如图3．小明利用皮尺测量，求出了小水池的最大宽度AB ，其测量及求解过程如下：测量过程：(ⅰ)在小水池外选点C ，如图4，测得AC =am ，BC =bm ；(ⅱ)分别在AC ，BC ，上测得CM =a 3m ，CN =b3m ；测得MN =cm ．求解过程：由测量知，AC =a ，BC =b ，CM =a 3，CN =b3，∴CM CA=CN CB =13，又∵①，∴△CMN ∽△CAB ，∴MN AB=13．又∵MN =c ，∴AB =②m ．故小水池的最大宽度为m ．(1)补全小明求解过程中①②所缺的内容；(2)小明求得AB 用到的几何知识是；(3)小明仅利用皮尺，通过5次测量，求得AB ．请你同时利用皮尺和测角仪，通过测量长度、角度等几何量，并利用解直角三角形的知识求小水池的最大宽度AB ，写出你的测量及求解过程．要求：测量得到的长度用字母a ，b ，c ⋯表示，角度用α，β，γ⋯表示；测量次数不超过4次(测量的几何量能求出AB ，且测量的次数最少，才能得满分)．12(2023秋·山西运城·九年级统考期末)综合与实践问题情境：如图1，在Rt△ABC中，∠C=90°，AC=3，BC=4，点D是AC上一点，将△BCD沿直线BD折叠，点C落在AB上的点E，连接DE．独立思考(1)如图1，求tan∠DBC的值；问题拓展如图2，点F是图1中AB上一动点，连接CF，交BD于点G．(2)当点F是AB的中点时，求证：DGBG =49；(3)当点G是BD的中点时，请你直接写出AFBF的值．13(2023·湖南郴州·统考中考真题)已知△ABC是等边三角形，点D是射线AB上的一个动点，延长BC 至点E，使CE=AD，连接DE交射线AC于点F．(1)如图1，当点D在线段AB上时，猜测线段CF与BD的数量关系并说明理由；(2)如图2，当点D在线段AB的延长线上时，①线段CF与BD的数量关系是否仍然成立？请说明理由；②如图3，连接AE．设AB=4，若∠AEB=∠DEB，求四边形BDFC的面积．14(2023·浙江·九年级专题练习)已知：如图，四边形ABCD是平行四边形，在边AB的延长线上截取BE=AB，点F在AE的延长线上，CE和DF交于点M，BC和DF交于点N，联结BD．(1)求证：△BND∽△CNM；(2)如果AD2=AB•AF，求证：CM•AB=DM•CN．15(2023·湖北武汉·统考模拟预测)问题背景：如图1，在四边形ABDC中，点F，E，G分别在AB，AD，AC上，EF∥BD，EG∥CD，求证：EFBD =EG DC尝试应用：如图2，AM是△ABC的中线，点E在AM上，直线BE交AC于点G，直线CE交AB于点F，若BE EC =2，求EF EG的值．迁移拓展：如图3，在等边△ABC 中，点D 在BC 上，点E 在AD 上，若BD =mDC ，∠BEC =120°，直接写出BE CE的值．(用含m 的式子表示)16(2023·浙江杭州·统考中考真题)在边长为1的正方形ABCD 中，点E 在边AD 上(不与点A ，D 重合)，射线BE 与射线CD 交于点F ．(1)若ED =13，求DF 的长．(2)求证：AE ⋅CF =1．(3)以点B 为圆心，BC 长为半径画弧，交线段BE 于点G ．若EG =ED ，求ED 的长．17(2022·四川内江·中考真题)如图，在矩形ABCD 中，AB =6，BC =4，点M 、N 分别在AB 、AD 上，且MN ⊥MC ，点E 为CD 的中点，连接BE 交MC 于点F ．(1)当F 为BE 的中点时，求证：AM =CE ；(2)若EF BF =2，求AN ND 的值；(3)若MN ∥BE ，求AN ND的值．18(2023•重庆中考模拟)问题提出：如图1，D 、E 分别在△ABC 的边AB 、AC 上，连接DE ，已知线段AD =a ，DB =b ，AE =c ，EC =d ，则S △ADE ，S △ABC 和a ，b ，c ，d 之间会有怎样的数量关系呢？问题解决：探究一：(1)看到这个问题后，我们可以考虑先从特例入手，找出其中的规律．如图2，若DE ∥BC ，则∠ADE =∠B ，且∠A =∠A ，所以△ADE ∽△ABC ，可得比例式：a a +b =c c +d 而根据相似三角形面积之比等于相似比的平方．可得S △ADE S △ABC =a 2a +b 2．根据上述这两个式子，可以推出：S △ADE S △ABC =a 2a +b2=a a +b ⋅a a +b =a a +b ⋅c c +d =ac a +b c +d．(2)如图3，若∠ADE =∠C ，上述结论还成立吗？若成立，请写出证明过程；着不成立，请说明理由．探究二：回到最初的问题，若图1中没有相似的条件，是否仍存在结论：S △ADE S △ABC =ac a +b c +d？方法回顾：两个三角形面积之比，不仅可以在相似的条件下求得，当两个三角形的底成高具有一定的关系时，也可以解决．如图4，D 在△ABC 的边上，做AH ⊥BC 于H ，可得：S △ABD S △ADC =12BD ⋅AH 12DC ⋅AH =BD DC ．借用这个结论，请你解决最初的问题．延伸探究：(1)如图5，D 、E 分别在△ABC 的边AB 、AC 反向延长线上，连接DE ，已知线段AD =a ，AB =b ，AE =c ，AC =d ，则S △ADE S △ABC=．(2)如图6，E 在△ABC 的边AC 上，D 在AB 反向延长线上，连接DE ，已知线段AD =a ，AB =b ，AE =c ，AC =d ，S △ADE S △ABC =．结论应用：如图7，在平行四边形ABCD 中，G 是BC 边上的中点，延长GA 到E ，连接DE 交BA 的延长线于F ，若AB =5，AG =4，AE =2，▱ABCD 的面积为30，则△AEF 的面积是．19(2023·河南郑州·校考三模)【问题发现】小明在一次利用三角板作图的过程中发现了一件有趣的事情：如图1，在Rt △ABC 中，∠A =30°，AB =6，点M 和点P 分别是斜边AB 上的动点，并且满足AM =BP ，分别过点M 和点P 作AC 边的垂线，垂足分别为点N 和点Q ，那么MN +PQ 的值是一个定值．问题：若AM =BP =2时，MN +PQ 值为；【操作探究】如图2，在Rt △ABC 中，∠C =90°，∠A =α，AB =m ；爱动脑筋的小明立即拿出另一个三角板进行了验证，发现果然和之前发现的结论一样，于是他猜想，对于任意一个直角三角形，当AM =BP 时，MN +PQ 的值都是固定的，小明的猜想对吗？如果对，请利用图2进行证明，并用含α和m 的式子表示MN +PQ 的值．【解决问题】如图3，在菱形ABCD 中，AB =8，BD =14．若M 、N 分别是边AD 、BC 上的动点，且AM =BN ，作ME ⊥BD ，NF ⊥BD ，垂足分别为E 、F ，则ME +NF 的值为．20(2022·湖北武汉·中考真题)问题提出：如图(1)，△ABC 中，AB =AC ，D 是AC 的中点，延长BC 至点E ，使DE =DB ，延长ED 交AB 于点F ，探究AF AB的值．(1)先将问题特殊化．如图(2)，当∠BAC =60°时，直接写出AF AB的值；(2)再探究一般情形．如图(1)，证明(1)中的结论仍然成立．问题拓展：如图(3)，在△ABC 中，AB =AC ，D 是AC 的中点，G 是边BC 上一点，CG BC =1n n <2 ，延长BC 至点E ，使DE =DG ，延长ED 交AB 于点F ．直接写出AF AB的值(用含n 的式子表示)．21(2023·浙江温州·统考中考真题)如图，已知矩形ABCD ，点E 在CB 延长线上，点F 在BC 延长线上，过点F 作FH ⊥EF 交ED 的延长线于点H ，连结AF 交EH 于点G ，GE =GH ．(1)求证：BE=CF．(2)当ABFH =56，AD=4时，求EF的长．。

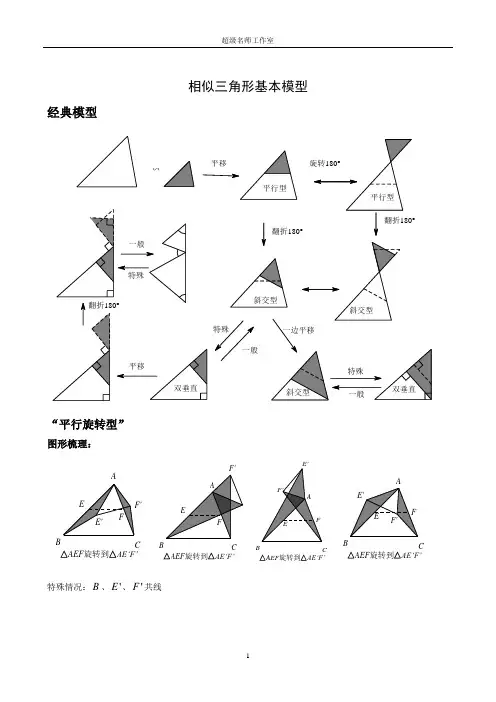
相似三角形基本模型经典模型“平行旋转型”图形梳理：AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’F'CBBCAEF 旋转到AE‘F’ABCAEF 旋转到AE‘F’特殊情况：B 、'E 、'F 共线AEF 旋转到AE‘F’CBAAB CEFE'F'AEF 旋转到AE‘F’C ，'E ，'F 共线AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBA母子型已知∠ACB=90°，AB ⊥CD ，则△CBD ∽△ABC ∽△ACD ．相似三角形常见的图形1、下面我们来看一看相似三角形的几种基本图形：（1） 如图：称为“平行线型”的相似三角形（有“A 型”与“X 型”图）(2) 如图：其中∠1=∠2，则△ADE ∽△ABC 称为“斜交型”的相似三角形。

（有“反A 共角型”、B(3)DB(2)D“反A 共角共边型”、 “蝶型”）（3）如图：称为“垂直型”（有“双垂直共角型”、“双垂直共角共边型（也称“射影定理型”“三垂直型”）(4)如图：∠1=∠2，∠B=∠D ，则△ADE ∽△ABC ，称为“旋转型”的相似三角形。

（5）母子型已知∠ACB=90°，AB ⊥CD ，则△CBD ∽△ABC ∽△ACD ．2、几种基本图形的具体应用：（1）若DE ∥BC （A 型和X 型）则△ADE ∽△ABC（2）射影定理 若CD 为Rt △ABC 斜边上的高（双直角图形）则Rt △ABC ∽Rt △ACD ∽Rt △CBD 且AC 2=AD ·AB ，CD 2=AD ·BD ，BC 2=BD ·AB ；（3）满足1、AC 2=AD ·AB ，2、∠ACD=∠B ，3、∠ACB=∠ADC ，都可判定△ADC ∽△ACB ． （4）当AD AEAC或AD ·AB=AC ·AE 时，△ADE∽△ACB ．BEACD12ABCD E12AAB BCC DD EE12412BBC (D)。

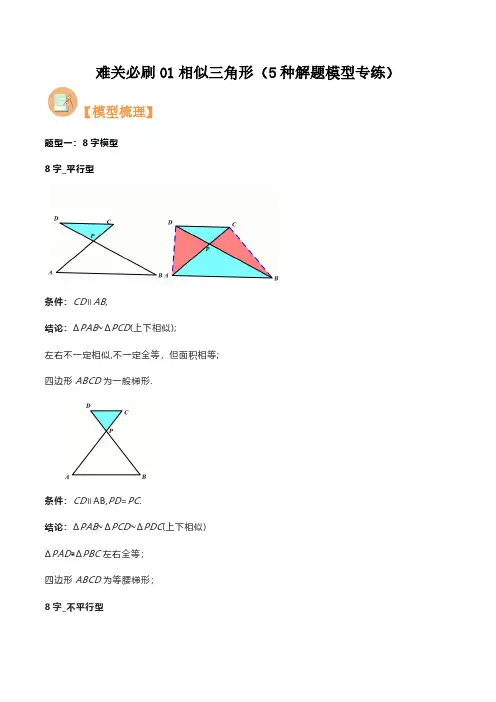
难关必刷01相似三角形（5种解题模型专练）【模型梳理】题型一：8字模型8字_平行型条件：CD∥AB,结论：ΔPAB∼ΔPCD(上下相似);左右不一定相似,不一定全等，但面积相等;四边形ABCD为一般梯形.条件：CD∥AB,PD=PC.结论：ΔPAB∼ΔPCD∼ΔPDC(上下相似)ΔPAD≅ΔPBC左右全等；四边形ABCD为等腰梯形；8字_不平行型条件：∠CDP =∠BAP .结论：ΔAPB ∼ΔDPC (上下相似);ΔAPD ∼ΔBPC (左右相似);题型二：A 字模型如图一DE如图二如图三题型三：一线三等角模型一线三等角指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。

或叫“K字模型”。

三直角相似可以看着是“一线三等角”中当角为直角时的特例，三直角型相似通常是以矩形或者正方形形为背景，或者在一条直线上有一个顶点在该直线上移动或者旋转的直角，几种常见的基本图形如下：当题目的条件中只有一个或者两个直角时，就要考虑通过添加辅助线构造完整的三直角型相似，这往往是很多压轴题的突破口，进而将三角型的条件进行转化。

一般类型：基本类型：同侧“一线三等角” 异侧“一线三等角”模型一：一线三直角图一 图二90;B ACE D ABC CDE ∠=∠=∠=∆∆ 如图一、二，已知：结论：（1）（2）A BDE =B CC D模型二：一线三等角图三 图四;B ACE D ABC CDE ABC CDE ACEα∠=∠=∠=∆∆∆∆∆ 如图三、四，已知：结论：（1）（2）A B D E =B CC D（3）当C 为B D 中点时，【方法点拨】基本模型：如图1，∠B =∠C =∠EDF 推出△BDE ∽△CFD （一线三等角）如图2，∠B =∠C =∠ADE 推出△ABD ∽△DC E （一线三等角）如图3，特别地，当D 时BC 中点时：△BDE ∽△DFE ∽△CFD 推出ED 平分∠BEF ，FD 平分∠EFC.题型四：旋转相似////,DE BC ADE AD E ABC ABD ACE ∆''∆∆∆∆∆ 旋转相似模型：已知：如图一，现将A D E 绕点A 旋转一定角度得到如图二得到和【方法点拨】基本模型：旋转放缩变换，图中必有两对相似三角形.题型五：母子型“子母型”相似的图形特点：有一个公共角，一对完全重合的边，一对半重合的边，一对完全不重合的边。

相似三角形重要模型-（双）A 字型与（双）8字型相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考的常考题型。

本专题重点讲解相似三角形的（双）A 字模型和（双）8（X ）字模型．A 字型和8 (X )字型的应用难点在于过分割点(将线段分割的点)作平行线构造模型，有的是直接作平行线，有的是间接作平行线(倍长中线就可以理解为一种间接作平行线) ， 这一点在模考中无论小题还是大题都是屡见不鲜的。

模型1. “A ”字模型 【模型解读与图示】“A ”字模型图形（通常只有一个公共顶点）的两个三角形有一个“公共角”（是对应角），再有一个角相等或夹这个公共角的两边对应成比例，就可以判定这两个三角形相似．图1 图2 图31）“A ”字模型 条件：如图1，DE ∥BC ；结论：△ADE ∽△ABC ⇔AD AB ＝AE AC ＝DEBC. 2）反“A ”字模型 条件：如图2，∠AE D ＝∠B ；结论：△ADE ∽△ACB ⇔AD AC ＝AE AB ＝DEBC .3）同向双“A ”字模型条件：如图3，EF ∥BC ；结论：△AEF ∽△ABC ，△AEG ∽△ABD ，△AGF ∽△ADC ⇔EG FG AGBD CD AD== 例1．（2022·浙江杭州·中考真题）如图，在ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，连接DE ，EF ，已知四边形BFED 是平行四边形，DE 1BC 4=．(1)若8AB =，求线段AD 的长．(2)若ADE 的面积为1，求平行四边形BFED 的面积．【答案】(1)2(2)6【分析】（1）利用平行四边形对边平行证明ADE ABC △△∽，得到DE ADBC AB=即可求出； （2）利用平行条件证明ADE EFC ∽，分别求出ADE EFC 与、ADE ABC 与的相似比，通过相似三角形的面积比等于相似比的平方分别求出EFC S V 、ABCS，最后通过BFEDABCEFCADESSSS=−−求出．(1)∵四边形BFED 是平行四边形，∴∥DE BC ，∴ADE ABC △△∽，∴DE ADBC AB=， ∵DE 1BC 4=，∴AD 1AB 4=，∴118244AD AB ==⨯=； (2)∵四边形BFED 是平行四边形，∴∥DE BC ，EF AB ∥，DE =BF ，∴,AED ECF EAD CEF ∠=∠∠=∠，∴ADE EFC ∽∴2ADE EFCSDE SFC ⎛⎫= ⎪⎝⎭， ∵DE 1BC 4=，DE =BF ，∴43FC BC DE DE DE DE =−=−=， ∴133DE DE FC DE ==，∴221139ADE EFCS DE SFC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， ∵ADE ABC △△∽，DE 1BC 4=，2211416ADE ABCS DE SBC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， ∵1ADE S =△，∴9,16EFCABCSS==，∴16916BFEDABCEFCADES SSS=−−=−−=．【点睛】本题考查了相似三角形，熟练掌握相似三角形的面积比等于相似比的平方、灵活运用平行条件证明三角形相似并求出相似比是解题关键．例2．（2023秋·安徽六安·九年级校考期末）如图，在ABC 中，BD 、CE 分别是AC 、AB 边上的高．求证：ACB AED ∽V V ．【答案】见详解【分析】先证明ACE ABD ∽，即有AE ACAD AB =，再结合A A ∠=∠，即可证明ACB AED ∽V V ．【详解】∵BD 、CE 分别是AC 、AB 边上的高，∴90AEC ADB ∠=∠=︒， ∵A A ∠=∠，∴ACE ABD ∽，∴AE ACAD AB =，又∵A A ∠=∠，∴ACB AED ∽V V ． 【点睛】本题主要考查了相似三角形的判定与性质，掌握三角形的判定与性质是解答本题的关键． 例3．（2022·山东东营·中考真题）如图，在ABC 中，点F 、G 在BC 上，点E 、H 分别在AB 、AC 上，四边形EFGH 是矩形，2,EH EF AD =是ABC 的高．8,6BC AD ==，那么EH 的长为____________．【答案】245##4.8【分析】通过四边形EFGH 为矩形推出E H B C ∥，因此△AEH 与△ABC 两个三角形相似，将AM 视为△AEH 的高，可得出AM EHAD BC =，再将数据代入即可得出答案． 【详解】∵四边形EFGH 是矩形，∴E H B C ∥，∴AEF ABC ∽， ∵AM 和AD 分别是△AEH 和△ABC 的高，∴,AM EH DM EF AD BC ==，∴6AM AD DM AD EF EF =−=−=−，∵=2EH EF ，代入可得：6268EF EF −=，解得12=5EF ， ∴1224=255EH ⨯=，故答案为：245．【点睛】本题考查了相似三角形的判定和性质及矩形的性质，灵活运用相似三角形的性质是本题的关键． 例4．（2022·浙江宁波·中考真题）(1)如图1，在ABC 中，D ，E ，F 分别为,,AB AC BC 上的点，,,DE BC BF CF AF =∥交DE 于点G ，求证：DG EG =．(2)如图2，在（1）的条件下，连接,CD CG ．若,6,3⊥==CG DE CD AE ，求DEBC的值． (3)如图3，在ABCD 中，45,︒∠=ADC AC 与BD 交于点O ，E 为AO 上一点，EG BD ∥交AD 于点G ，⊥EF EG交BC 于点F ．若40,︒∠=EGF FG 平分,10∠=EFC FG ，求BF 的长．【答案】(1)证明见详解(2)13(3)5+【分析】（1）利用∥DE BC ，证明,ADG ABF AEG ACF △△△△，利用相似比即可证明此问； （2）由（1）得DG EG =，CG DE ⊥，得出DCE 是等腰三角形，利用三角形相似即可求出DEBC的值； （3）遵循第（1）、（2）小问的思路，延长GE 交AB 于点M ，连接FM ，作MN BC ⊥，垂足为N ．构造出等腰三角形、含30°、45°角的特殊直角三角形，求出BN 、FN 的值，即可得出BF 的长． (1)解：∵DE BC ∥，∴,ADG ABF AEG ACF △△△△， ∴,==DG AG EG AG BF AF CF AF ，∴DG EGBF CF=．∵BF CF =，∴DG EG =． (2)解：由（1）得DG EG =，∵CG DE ⊥，∴6CE CD ==． ∵3AE =，∴9AC AE CE =+=．∵DE BC ∥，∴ADEABC ．∴13DE AE BC AC ==． (3)解：如图，延长GE 交AB 于点M ，连接FM ，作MN BC ⊥，垂足为N ．在ABCD 中，,45=∠=∠=︒BO DO ABC ADC ． ∵EG BD ∥，∴由（1）得=ME GE ，∵⊥EF EG ，∴10==FM FG ，∴∠=∠EFM EFG ． ∵40∠︒=EGF ，∴40EMF ∠=︒，∴50EFG ∠=︒． ∵FG 平分EFC ∠，∴50∠=∠=︒EFG CFG ， ∴18030∠=︒−∠−∠−∠=︒BFM EFM EFG CFG ．∴．在Rt FMN 中，sin 305,cos30=︒==︒=MN FM FN FM∵45,∠=︒⊥MBN MN BN ，∴5==BN MN ，∴5=+=+BF BN FN【点睛】本题考查了相似三角形的性质及判定、等腰三角形的性质及判定、解特殊的直角三角形等知识，遵循构第（1）、（2）小问的思路，构造出等腰三角形和特殊的直角三角形是解决本题的关键．例5. （2022•安庆一模）如图，在△ABC 中，点D 、E 、F 分别在边BC 、AB 、CA 上，且DE ∥CA ，DF ∥AB ．（1）若点D 是边BC 的中点，且BE ＝CF ，求证：DE ＝DF ；（2）若AD ⊥BC 于D ，且BD ＝CD ，求证：四边形AEDF 是菱形；（3）若AE ＝AF ＝1，求+的值．【分析】（1）根据中点和平行两个条件可得中点，从而可得DE 是△ABC 的中位线，进而可得DE ＝FC ，同理可得DF ＝BE ，即可解答；（2）根据已知易证四边形AEDF 是平行四边形，再利用等腰三角形的三线合一性质可得∠BAD ＝∠CAD ，然后利用平行线的性质可得∠＝∠CAD ，从而可得∠BAD ＝∠EDA ，进而可得EA ＝ED ，即可解答； （3）根据A 字模型相似三角形可知△BED ∽△BAC ，△CDF ∽△CBA ，从而可得＝，＝，然后把两个式子相加进行计算，即可解答．【解答】（1）证明：∵点D 是边BC 的中点，DE ∥CA ，∴点E 是AB 的中点，∴DE 是△ABC 的中位线，∴DE ＝AC ，∵点D 是边BC 的中点，DF ∥AB ，∴点F 是AC 的中点， ∴FC ＝AC ，∴DE ＝FC ，同理可得：DF ＝BE ，∵BE ＝FC ，∴DE ＝DF ；（2）证明：∵DE ∥CA ，DF ∥AB ，∴四边形AEDF 是平行四边形， ∵AD ⊥BC ，BD ＝CD ，∴AD 是BC 的垂直平分线，∴AB ＝AC ，∴∠BAD ＝∠CAD ，∵DE ∥AC ，∴∠EDA ＝∠CAD ，∴∠BAD＝∠EDA，∴EA＝ED，∴四边形AEDF是菱形；（3）∵DE∥CA，∴∠EDB＝∠C，∵∠B＝∠B，∴△BED∽△BAC，∴＝，∵DF∥AB，∴∠B＝∠FDC，∵∠C＝∠C，∴△CDF∽△CBA，∴＝，∴+＝+＝＝1，∵四边形AEDF是平行四边形，∴DE＝AF，DF＝AE，∵AE＝AF＝1，∴DE＝DF＝1，∴+＝1，∴+的值为1．【点评】本题考查了相似三角形的判定与性质，全等三角形的判定与性质，线段垂直平分线的性质，分式的化简求值，菱形的判定与性质，熟练掌握菱形的判定与性质，以及A字模型相似三角形的关键．模型2. “X”字模型（“8”模型）【模型解读与图示】“8”字模型图形的两个三角形有“对顶角”，再有一个角相等或夹对顶角的两边对应成比例就可以判定这两个三角形相似．图1 图2 图3 图41）“8”字模型条件：如图1，AB∥CD；结论：△AOB∽△COD⇔ABCD＝OAOC＝OBOD.2）反“8”字模型条件：如图2，∠A＝∠D；结论：△AOB∽△DOC⇔ABCD＝OAOD＝OBOC.3）平行双“8”字模型条件：如图3，AB∥C D；结论：AE BE ABDF CF CD==4）斜双“8”字模型条件：如图4，∠1＝∠2；结论：△AOD∽△B O C，△AOB∽△DOC⇔∠3＝∠4.例1．（2022·河北·中考真题）如图是钉板示意图，每相邻4个钉点是边长为1个单位长的小正方形顶点，钉点A ，B 的连线与钉点C ，D 的连线交于点E ，则（1）AB 与CD 是否垂直？______（填“是”或“否”）；（2）AE ＝______．【答案】 是【分析】（1）证明△ACG ≌△CFD ，推出∠CAG =∠FCD ，证明∠CEA =90°，即可得到结论；（2）利用勾股定理求得AB 的长，证明△AEC ∽△BED ，利用相似三角形的性质列式计算即可求解． 【详解】解：（1）如图：AC =CF =2，CG =DF =1，∠ACG =∠CFD =90°， ∴△ACG ≌△CFD ， ∴∠CAG =∠FCD ， ∵∠ACE +∠FCD =90°，∴∠ACE +∠CAG =90°，∴∠CEA =90°，∴AB 与CD 是垂直的，故答案为：是；（2）AB ∵AC ∥BD ，∴△AEC ∽△BED ，∴AC AEBD BE =，即23AE BE =，∴2AE BE =∴AE =25BE【点睛】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，解答本题的关键是明确题意，找出所求问题需要的条件．例2.（2022·广西·中考模拟）如图，已知在△ABC 中，BE 平分∠ABC 交AC 于E ，点D 在BE 延长线上，且BA •BC ＝BD •BE ．（1）求证：△ABD ∽△EBC ；（2）求证：AD 2＝BD •DE ．【答案】见解析【解答】证明：（1）∵BE 平分∠ABC ，∴∠ABD ＝∠EBC ， ∵BA •BC ＝BD •BE ．即AB BC=BD BE，∴△ABD ∽△EBC ；（2）∵△ABD ∽△EBC ，∴∠BAD ＝∠BEC ，∠ADB ＝∠BCE ， ∵∠AED ＝∠BEC ，∴∠BAD ＝∠AED ，∴△ADE ∽△BEC ， ∴△AED ∽△ABD ，∴AD BD=DE AD，即AD 2＝BD •DE ．例3.（2023·浙江九年级期中）如图，AD 与BC 交于点O ，EF 过点O ，交AB 与点E ，交CD 与点F ，BO ＝1，CO ＝3，AO =32，DO =92．（1）求证：∠A ＝∠D ．（2）若AE ＝BE ，求证：CF ＝DF ．【答案】【解析】证明：（1）∵BO ＝1，CO ＝3，AO =32，DO =92．∴OB OC =AO DO，∵∠AOB ＝∠COD ，∴△OAB ∽△ODC ，∴∠A ＝∠D ． （2）∵∠A ＝∠D ，∴AB ∥CD ， ∴AE DF =OE OF ，BE CF =OE OF ，∴AE DF =BECF． ∵AE ＝BE ，∴CF ＝DF ．例4．（2022·广西贵港·中考真题）已知：点C ，D 均在直线l 的上方，AC 与BD 都是直线l 的垂线段，且BD 在AC 的右侧，2BD AC =，AD 与BC 相交于点O ． (1)如图1，若连接CD ，则BCD △的形状为______，AOAD的值为______； (2)若将BD 沿直线l 平移，并以AD 为一边在直线l 的上方作等边ADE ． ①如图2，当AE 与AC 重合时，连接OE ，若32AC =，求OE 的长；②如图3，当60ACB ∠=︒时，连接EC 并延长交直线l 于点F ，连接OF ．求证：OF AB ⊥．【答案】(1)等腰三角形，13(2)①OE =②见解析【分析】（1）过点C 作CH ⊥BD 于H ，可得四边形ABHC 是矩形，即可求得AC =BH ，进而可判断△BCD 的形状，AC 、BD 都垂直于l ，可得△AOC ∽△BOD ，根据三角形相似的性质即可求解．（2）①过点E 作EF AD ⊥于点H ，AC ，BD 均是直线l 的垂线段，可得//AC BD ，根据等边三角形的性质可得30BAD ∠=︒，再利用勾股定理即可求解．②连接CD ，根据//AC BD ，得60CBD ACB ∠=∠=︒，即BCD △是等边三角形，把ABD △旋转得90ECD ABD ∠=∠=︒，根据30°角所对的直角边等于斜边的一般得到13AF AO AB AD ==，则可得AOF ADB △∽△，根据三角形相似的性质即可求证结论． (1)解：过点C 作CH ⊥BD 于H ，如图所示：∵AC ⊥l ，DB ⊥l ，CH ⊥BD ，∴∠CAB =∠ABD =∠CHB =90°，∴四边形ABHC 是矩形，∴AC =BH ， 又∵BD =2AC ，∴AC=BH=DH ，且CH ⊥BD ，∴BCD △的形状为等腰三角形， ∵AC 、BD 都垂直于l ，∴△AOC ∽△BOD ，122AO AC AC DO DB AC ∴===，即2DO AO =， 133AO AO AD AO DO A AO O ∴===+，故答案为：等腰三角形，13．(2)①过点E 作EF AD ⊥于点H ，如图所示：∵AC ，BD 均是直线l 的垂线段，∴//AC BD ，∵ADE 是等边三角形，且AE 与AC 重合，∴∠EAD =60°，∴60ADB EAD ∠=∠=︒，∴30BAD ∠=︒，∴在Rt ADB 中，2AD BD =，=AB ，又∵2BD AC =，32AC =，∴6,AD AB ==∴132AH DH AD ===，又Rt ADB ，∴EH =又由（1）知13AO AD =，∴123AO AD ==，则1OH =，∴在Rt EOH △中，由勾股定理得：OE =②连接CD ，如图3所示：∵//AC BD ，∴60CBD ACB ∠=∠=︒，∵BCD △是等腰三角形，∴BCD △是等边三角形，又∵ADE 是等边三角形， ∴ABD △绕点D 顺时针旋转60︒后与ECD 重合，∴90ECD ABD ∠=∠=︒， 又∵60BCD ACB ∠=∠=︒，∴30ACF FCB FBC ∠=∠=∠=︒， ∴2FC FB AF ==，∴13AF AO AB AD ==，又OAF DAB ∠=∠，∴AOF ADB △∽△， ∴90AFO ABD ∠=∠=︒，∴OF AB ⊥．【点睛】本题考查了矩形的判定及性质、三角形相似的判定及性质、等边三角形的判定及性质、勾股定理的应用，熟练掌握三角形相似的判定及性质和勾股定理的应用，巧妙借助辅助线是解题的关键．模型3. “AX ”字模型（“A 8”模型） 【模型解读与图示】图1 图2 图3 1）一“A ”一“8”模型条件：如图1，DE ∥BC ；结论：△ADE ∽△ABC ，△DEF ∽△CBF ⇔AD AE DE DF FEAB AC BC FC BF====2）两“A ”一“8”模型条件：如图2，DE ∥AF ∥BC ；结论：111BC DE AF+=. 3）四“A ”一“8”模型 条件：如图3，DE ∥AF ∥BC,1111BC DE AF AG+==；结论：AF =AG 例1．（2022·山东东营·中考真题）如图，点D 为ABC 边AB 上任一点，DE BC ∥交AC 于点E ，连接BE CD 、相交于点F ，则下列等式中不成立．．．的是（ ）A ．AD AEDB EC= B ．DE DFBC FC= C ．DE AEBC EC= D ．EF AEBF AC= 【答案】C【分析】根据平行线分线段成比例定理即可判断A ，根据相似三角形的性质即可判断B 、C 、D ． 【详解】解：∵∥DE BC ，∴AD AEBD EC =，△DEF ∽△CBF ，△ADE ∽△ABC ，故A 不符合题意； ∴DE DF EF CB CF BF ==，DE AECB AC =，故B 不符合题意，C 符合题意； ∴EF AEBF AC =，故D 不符合题意；故选C ． 【点睛】本题主要考查了相似三角形的性质与判定，平行线分线段成比例定理，熟知相似三角形的性质与判定，平行线分线段成比例定理是解题的关键．例2．（2023·浙江·杭州九年级期中）如图， ABC 中，中线AD ，BE 交于点F ，//EG BC 交AD 于点G ．（1）求AGGF的值．（2）如果BD =4DF =，请找出与BDA V 相似的三角形，并挑出一个进行证明．【答案】（1）3；（2）BDA FGE ∽△△，证明见解析 【分析】（1）先证明AGE ADC △∽△，再证明GEF DBF ∽△△，得到2DF GF =，则问题可解； （2）根据题意分别证明BDA FDB ∽△△，BDA FGE ∽△△问题可证． 【详解】解：（1）D Q 是BC 的中点，E 是AC 的中点，BD CD ∴=，AE CE =，//GE BC ，AGE ADC ∴∽△△，12AG GE AE AD CD AC ∴===，AG GD ∴=，2GE CD BD ==，//GE BC ，GEF DBF ∴∽△△，12GE GF BD DF ∴==，2DF GF ∴=，3AG DG GF ∴==，3AGGF ∴=．（2）当BD =4DF =时，由（1）可得 122GF DF ==，36AG DG GF ===，212AD AG ==，12GE BD ==44BD DF ==AD BD ==，AD BD BD DF ∴=，又BDG ADB ∠=∠，BDA FDB ∴∽△△，3GEGF =AD BD ==，AD GE BD GF ∴=，//GE BC ，ADB EGF ∴∠=∠，BDA FGE ∴∽△△．【点睛】本题考查了相似三角形的性质和判定，解答关键是根据题意选择适当方法证明三角形相似． 例2.（2023·广东九年级期中）如图，在菱形ABCD 中，∠ADE 、∠CDF 分别交BC 、AB 于点E 、F ，DF 交对角线AC 于点M ，且∠ADE ＝∠CDF ．（1）求证：CE ＝AF ；（2）连接ME ，若CE BE ＝CDCE，AF ＝2，求ME 的长．【解析】解：（1）∵四边形ABCD 是菱形，∴AD ＝CD ，∠DAF ＝∠DCE ， 又∵∠ADE ＝∠CDF ，∴∠ADE ﹣∠EDF ＝∠CDF ﹣∠EDF ，∴∠ADF ＝∠CDE ，在△ADF 和△CDE 中，ADF CDFAD CD DAF DCE ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ADF ≌△CDE ，∴CE ＝AF ．（2）∵四边形ABCD 是菱形，∴AB ＝BC ，由（1）得：CE ＝AF ＝2，∴BE ＝BF ，设BE ＝BF ＝x ，∵CE BE ＝CDCE，AF ＝2，∴222x x +=，解得x1，∴BE ＝BF1，∵CE BE ＝CD CE ，且CE ＝AF ，∴CE BE ＝CD CE ＝CD AF， ∵∠CMD ＝∠AMF ，∠DCM ＝∠AMF ，∴△AMF ∽△CMD ，∴CD CMAF AM=， ∴CD CM CEAF AM BE==，且∠ACB ＝∠ACB,∴△ABC ～△MEC, ∴∠CAB ＝∠CME=∠ACB ，∴ME=CE=2．例3. （2022·浙江九年级期中）如图，已知AB ∥CD ，AC 与BD 相交于点E ，点F 在线段BC 上，AB CD =12，BFCF =12．（1）求证：AB ∥EF ；（2）求S △ABE ：S △EBC ：S △ECD ．【答案】见解析【解析】（1）证明：∵AB ∥CD ，∴AB CD =BE ED =12，∵BF CF =12，∴BE ED =BFFC，∴EF ∥CD ，∴AB ∥EF ． （2）设△ABE 的面积为m ．∵AB ∥CD ，∴△ABE ∽△CDE ，∴S △ABE S △EDC =（AB CD ）2=14，∴S △CDE ＝4m ，∵AE CE =AB CD =12，∴S △BEC ＝2m ， ∴S △ABE ：S △EBC ：S △ECD ＝m ：2m ：4m ＝1：2：4．例4．（2022•安庆模拟）在四边形ABCD 中，对角线AC 、BD 相交于点O ． （1）如图①，若四边形ABCD 为矩形，过点O 作OE ⊥BC ，求证：OE ＝CD ．（2）如图②，若AB ∥CD ，过点O 作EF ∥AB 分别交BC 、AD 于点E 、F ．求证：＝2．（3）如图③，若OC 平分∠AOB ，D 、E 分别为OA 、OB 上的点，DE 交OC 于点M ，作MN ∥OB 交OA 于一点N ，若OD ＝8，OE ＝6，直接写出线段MN 长度．【分析】（1）由OE ⊥BC ，DC ⊥BC ，可知EO ∥CD ，且OB ＝OD ，可得结论； （2）由△DFO ∽△DAB ，得，同理，，，利用等式的性质将比例式相加，从而得出结论；（3）作DF ∥OB 交OC 于点F ，连接EF ，可知△ODF 是等腰三角形，得DO ＝DF ＝8，由△DMF ∽△EMO ，可得EM ＝，由△DMN ∽△DOE ，得，从而得出答案．【解答】（1）证明：∵四边形ABCD 是矩形，∴O 是AC 中点，AB ⊥BC ， ∵OE ⊥BC ，∴OE ∥AB ，∴E 是BC 中点，∴OE ＝； （2）证明：∵EF ∥AB ，∴△DFO ∽△DAB ，∴， 同理，，，∴＝，∴，即； （3）解：作DF ∥OB 交OC 于点F ，连接EF ，∵OC 平分∠AOB ，∴∠AOC ＝∠BOC ，∵DF ∥OB ，∴∠DFO ＝∠BOC ＝∠AOC ， ∴△ODF 是等腰三角形，∴DO ＝DF ＝8，∵DF ∥OE ，∴△DMF ∽△EMO ，∴，∴EM ＝，∴，∵MN ∥OE ，∴△DMN ∽△DOE ，∴，∴，∴MN ＝．【点评】本题是相似形综合题，主要考查了矩形的性质，相似三角形的判定与性质，等腰三角形的性质，对比例式进行恒等变形是解题的关键．课后专项训练1. （2021·山东淄博·中考真题）如图，,AB CD 相交于点E ，且////AC EF DB ，点,,C F B 在同一条直线上．已知,,AC P EF r DB q ===，则,,p q r 之间满足的数量关系式是（ ）A ．111r q p+=B ．112p r q+= C ．111p q r += D ．112q r p+=【答案】C【分析】由题意易得BEF BAC ∽△△，CEF CDB ∽，则有EF BF AC BC =，EF CF BD BC =，然后可得1EF EFAC BD +=，进而问题可求解．【详解】解：∵////AC EF DB ，∴BEF BAC ∽△△，CEF CDB ∽， ∴EF BFAC BC =，EF CF BD BC =，∴1EF EF BF CFAC BD BC BC +=+=，∵,,AC P EF r DB q ===， ∴1r r p q +=，即111p q r +=； 故选C ．【点睛】本题主要考查相似三角形的性质与判定，熟练掌握相似三角形的性质与判定是解题的关键． 九年级校考期末）如图，ABC 中，:PEDPDGS S=（ 【答案】A【分析】根据角平分线的定义及平行线的性质可知PEH △是等腰三角形，再根据相似三角形的判定与性质可知12ED EH FD PF ==，进而解答即可． 【详解】解：过点E 作PF EH ∥AD 的延长线于点H ， ∵AD 是ABC 的角平分线， ∴BAD CAD ∠=∠， ∵PE AB ∥，PF AC ∥，∴BAC EPD ∠=∠，CAD DPF ∠=∠， ∴EPD FPD ∠=∠， ∵EH PF ∥， ∴H DPF ∠=∠， ∴EPD H ∠=∠， ∴PEH △是等腰三角形， ∴PE EH =， ∵3PE =，∴3PE EH ==， ∵EH PF ∥， ∴PFD HED ∠=∠， ∴EDH FDP ∽， ∴ED EHFD PF =， ∵6PF =，∴3162ED EH FD PF ===， ∴2FD ED =，∴设ED a =，2FD a =， ∴3EF ED FD a =+=， ∵G 是EF 的中点，∴1322EG EF a ==， ∴3122DG EG ED a a a=−=−=， 过P 作PM ED ⊥，垂足为M ， ∴12PEDSED PM=⋅⋅，12PDGS DG PM =⋅⋅，∴122:11122PED PDGED PMSaS DG PM a ⋅⋅===⋅⋅，故选：A ．【点睛】本题考查了平行线的性质，相似三角形的判定与性质，角平分线的定义，中点的定义，等腰三角形的判定与性质，掌握相似三角形的判定与性质是解题的关键．3．（2022秋·九年级单元测试）如图，在平行四边形ABCD 中，E 为边AD 的中点，连接AC，BE 交于点F ．若△AEF 的面积为2，则△ABC 的面积为( )A ．8B ．10C ．12D ．14【答案】C【分析】先利用平行四边形的性质得AD BC ∥，AD=BC ，由AE BC ∥可判断△AEF ∽△CBF ，根据相似三角形的性质得12EF AF AE BF CF BC ===，然后根据三角形面积公式得16AEF ABC S S ∆∆=，则=6=12ABC AEF S S ∆∆．【详解】∵平行四边形ABCD ∴AD BC ∥，AD=BC ∵E 为边AD 的中点 ∴BC=2AE ∵AE BC ∥ ∴∠EAC=∠BCA 又∵∠EFA=∠BFC ∴△AEF ∽△CBF如图，过点F 作FH ⊥AD 于点H ，FG ⊥BC 于点G ， 则12EF AF AE HF BF CF BC FG ====，∴111221362AEF ABC AE FH BC FHS S BC FH BC HG ∆∆⋅⋅⋅===⋅⋅⋅，∵△AEF 的面积为2 ∴66212ABC AEF S S ∆∆==⨯=故选C ．【点睛】本题考查了相似三角形的性质，属于同步基础题．A ．43AC =，123BD = C ．6AC =，83BD = 【答案】D【分析】过点B 作BO AD ∥交AC 于点O ，证明AED OEB ∽，可求得OE AO =理求出BO 的长，进而可求出AC 的长，再根据勾股定理求出BE 的长，进而求出BD 的长． 【详解】过点B 作BO AD ∥交AC 于点O ，如图所示：∵AC AD ⊥，BO AD ∥， ∴90DAC BOA ︒∠=∠=． ∵AED OEB ∠=∠， ∴AED OEB ∽， ∴BE EO BODE AE DA ==． ∵3DE BE =，∴13EO BO AE DA ==．∵AE =，∴OE∴AO =∵AB AC =，75ACB ∠=︒， ∵75ABC ACB ∠=∠=︒， ∴30BAC ∠=︒， ∴2AB BO =．在Rt AOB △中，222BO AO AB +=，即(()2222BO BO +=，解得：4BO =，∴8AB AC ==．∵OE 4BO =，∴BE ==∴3DE BE ==∴BD BE DE =+= 故选D ．【点睛】本题考查了相似三角形的判定与性质，等腰三角形的性质，含30度角的直角三角形的性质，勾股定理以及平行线的性质，解题的关键是利用勾股定理求出BE 的长度．A ．45B ．54【答案】C【分析】先由平行四边形性质得到AB CD ∥，AB CD =，证明AOB COE ∽△△得到249AOB COE S AB CE S æöç÷==ç÷èø△△，进而得到221AB DE ==，再证明AFB DFE ∽求解即可．【详解】解：∵四边形ABCD 是平行四边形， ∴AB CD ∥，AB CD =， ∴ABO E ∠=∠，BAO ECO ∠=∠，∴AOB COE ∽△△， ∴249AOB COE S AB CE S æöç÷==ç÷èø△△， ∴23AB CE =，则221AB DE ==，∵AFB DFE ∠=∠，ABF E ∠=∠， ∴AFB DFE ∽， ∴2AF ABDF DE ==，故选：C ．【点睛】本题考查平行四边形的性质、相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解答的关键．6．（2023·福建福州·校考二模）在数学综合实践课上，某学习小组计划制作一个款式如图所示的风筝．在骨架设计中，两条侧翼的长度设计50cm AB AC ==，风筝顶角BAC ∠的度数为110︒，在AB AC ，上取D ，E 两处，使得AD AE =，并作一条骨架AF DE ⊥．在制作风筝面时，需覆盖整个骨架，根据以上数据，B ，C 两点间的距离大约是（ ）（参考数据：sin550.82cos550.57tan55 1.43︒≈︒≈︒≈，，）A ．41cmB ．57cmC ．82cmD ．143cm【答案】C【分析】设AF 与DE 交于点G ，连接BC ，交AF 于点H ，根据已知易证ADE ABC △△∽，然后利用相似三角形的性质可得ADE ABC =∠∠，从而可得DE BC ∥，进而可得BC AF ⊥，再利用等腰三角形的三线合一性质可得2BC BH =，1552BAH BAC ∠=∠=︒，最后在Rt BAH 中，利用锐角三角函数的定义求出BH 的长，即可解答．【详解】解：设AF 与DE 交于点G ，连接BC ，交AF 于点H ，AD AE =，AB AC =，∴AD AEAB AC =， DAE BAC ∠=∠， ADE ABC ∴△△∽， ADE ABC ∴∠=∠， DE BC ∴∥，AF DE ⊥，BC AF ∴⊥，AB AC =，AF BC ⊥，2BC BH ∴=，1552BAH BAC ∠=∠=︒，在Rt BAH 中，50cm AB =，sin 55500.8241cm BH AB ∴=⋅︒≈⨯=， 282cm BC BH ∴==，B ∴，C 两点间的距离大约是82cm ，故选：C ．【点睛】本题考查了解直角三角形的应用，相似三角形的判定与性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．7．（2023·广东深圳·校考三模）如图，在Rt ABC 中，906ACB AC BC ∠=︒==，，D 是AB 上一点，点E 在BC上，连接CD AE ，交于点F ，若452CFE BD AD ∠=︒=，，则CE ＝ ．【答案】2【分析】过D 作DH 垂直AC 于H 点，过D 作DG AE ∥交BC 于G 点，先利用解直角三角形求出CD 的长，其次利用CDG CBD ∽，求出CG 的长，得出BG 的长，最后利用BDG BAE ∽，求出BE 的长，最后得出答案．【详解】解：如图：过D 作DH 垂直AC 于H 点，过D 作DG AE ∥交BC 于G 点，∵在Rt ABC 中，6AC BC ==，∴AB =又∵2BD AD =，∴AD =，∴在等腰直角三角形AHD 中，2AH DH ==， ∴624CH =−=，在Rt CHD 中，CD =∵DG AE ∥，∴45CFE CDG ∠=∠=︒，45B ∠=︒， ∴CDG B ∠=∠， 又∵DCG BCD ∠=∠，∴CDG CBD ∽， ∴CD CGCB CD =， ∴ 2CD CG CB =⋅，即206CG =， ∴CG =103 ，∴BG BC CG =−=108633−=，又∵DG AE ∥，∴BDG BAE ∽， 又∵2BD AD ＝， ∴23BD BG BA BE ==，又83BG =，∴342BE BG =⨯=，∴642CE =−=， 故答案为：2．【点睛】本题考查勾股定理，等腰直角三角形性质及相似三角形的判定与性质综合，解题关键在于正确做出辅助线，利用相似三角形的性质得出对应边成比例求出答案．8．（2023春·山东东营·八年级统考期末）如图，在ABC 中，D ，E ，F 分别是AB ，AC ，BC 上的点，且DE BC ∥，EF AB ∥，:2:3AD DB =，20cm BC =，则BF = cm ．【答案】8【分析】首先根据平行四边形的判定证明四边形BDEF 是平行四边形，则BF DE =，然后根据相似三角形的性质即可求解．【详解】解：∵DE BC ∥，EF AB ∥， ∴四边形BDEF 是平行四边形， ∴BF DE =． ∵:2:3AD DB =， ∴:2:5AD AB =． ∵DE BC ∥， ∴ADE ABC △△∽，∴::2:5DE BC AD AB ==，即:202:5DE =， ∴8DE =， ∴8BF =． 故BF 的长为8cm ． 故答案为：8【点睛】本题主要考查平行四边形的判定及性质，相似三角形的判定与性质，掌握这些性质及判定是解题的关键．九年级校考阶段练习）如图，在ABC 中，【答案】【分析】如图所示，取AC 中点H ，连接DH ，先求出5BC =，再由线段垂直平分线的性质得到DE DB ⊥，点D 为AB 中点，证明BD DE =得到DE BD ===AD BD ==得到12.52DH BC DH BC ==∥，，进而证明DFH EFC △∽△，得到57DF DE ==，利用勾股定理可得AF ==．【详解】解：如图所示，取AC 中点H ，连接DH ， ∵61BE CE CE ==，， ∴6BE =， ∴5BC =，∵DE 垂直平分线段AB ， ∴DE DB ⊥，点D 为AB 中点， 又∵=45ABC ∠︒，∴9045E DBE =︒−=︒∠∠， ∴E DBE =∠， ∴BD DE =，∴2DE BD ===∴AD BD ==∵点H 为AC 中点，点D 为AB 中点， ∴DH 为ABC 中位线， ∴12.52DH BC DH BC ==∥，，∴DFH EFC △∽△， ∴2.5512DF DH EF CE ===，∴577DF DE ==，∴AF ==，故答案为：．【点睛】本题主要考查了相似三角形的性质与判定，三角形中位线定理，勾股定理，线段垂直平分线的性质，等腰直角三角形的性质与判定等等，正确作出辅助线构造相似三角形是解题的关键．【答案】45【分析】如图所示，延长CD 交各格线于点D ，证明AOC BOD ∽，即可得到45OA AC OB BE ==． 【详解】解：如图所示，延长CD 交网格线于点D ， 由网格的特点可知点E 在格点处， ∵AC BE ， ∴AOC BOD ∽， ∴45OA AC OB BE ==， 故答案为：45．【点睛】本题主要考查了相似三角形的性质与判定，正确作出辅助线构造相似三角形是解题的关键．11.已知：如图，点D ，F 在△ABC 边AC 上，点E 在边BC 上，且DE ∥AB ，CD 2＝CF •CA ． （1）求证：EF ∥BD ；（2）如果AC •CF ＝BC •CE ，求证：BD 2＝DE •BA ．【答案】见解析【解析】证明：（1）∵DE ∥AB ，∴CD AC =CE CB，∵CD 2＝CF •CA ．∴CD AC=CF CD，∴CF CD=CE CB，∴EF ∥BD ；（2）∵EF ∥BD ，∴∠CEF ＝∠CBD ，∵AC •CF ＝BC •CE ，∴AC BC =CECF ，且∠C ＝∠C ，∴△CEF ∽△CAB ，∴∠CEF ＝∠A ，∴∠DBE ＝∠A ，∵DE ∥AB ，∴∠EDB ＝∠DBA ，且∠DBE ＝∠A ，∴△BAD ∽△DBE ，∴BA BD =BDDE∴BD 2＝BA •DE12．[阅读理解]构造“平行八字型”全等三角形模型是证明线段相等的一种方法，我们常用这种方法证明线段的中点问题．例如：如图，D 是△ABC 边AB 上一点，E 是AC 的中点，过点C 作CF ∥AB ，交DE 的延长线于点F ，则易证E 是线段DF 的中点．[经验运用]请运用上述阅读材料中所积累的经验和方法解决下列问题．（1）如图1，在正方形ABCD 中，点E 在AB 上，点F 在BC 的延长线上，且满足AE ＝CF ，连接EF 交AC 于点G ．求证：①G 是EF 的中点；②CG ＝2BE ； [拓展延伸]（2）如图2，在矩形ABCD 中，AB ＝2BC ，点E 在AB 上，点F 在BC 的延长线上，且满足AE ＝2CF ，连接EF 交AC 于点G ．探究BE 和CG 之间的数量关系，并说明理由；（3）如图3，若点E 在BA 的延长线上，点F 在线段BC 上，DF 交AC 于点H ，BF ＝2，CF ＝1，（ 2）中的其它条件不变，请直接写出GH 的长．【答案】（1）①详见解析；②详见解析；（2）BE ，理由详见解析；（3．【分析】（1）①过点E 作EI ∥BC 交AC 于点I ，证明△EIG ≌△FCG （ASA ），得出EG ＝FG 即可；②由等腰直角三角形的性质得出 AI ，由平行线得出AIAE＝IC EB IC ，由全等三角形的性质得出IG ＝CG ＝12IC ，即可得出结论；（2）作EI ∥BC 交AC 于点I ，由三角函数证出AE ＝2IE ，得出IE ＝CF ，证△EIG ≌△FCG （ASA ），得出EG ＝FG ，IG ＝CG ，设IE ＝a ，则AE ＝2a ，求出AE AI，则IC EB ＝AI AE ，得出IC EB ，即可得出结果；（3）作FP ∥AB 交AC 于P ，则FP ∥CD ，∠CFP ＝∠ABC ＝90°，∠CPF ＝∠CAB ，则tan ∠CPF ＝CF PF＝tan ∠CAB ＝BCAB＝12，求出AE ＝PF ＝2，BC ＝3，CD ＝AB ＝2BC ＝6，AC ＝△CPF ∽△CAB ，得出PCAC ＝CF BC ＝13，求出PC ＝13AC PA ＝AG ＝PG △PFH ∽△CDH ，得出PH CH ＝PF CD ＝13，得出PH ＝14PC 【详解】（1）证明：①过点E 作EI ∥BC 交AC 于点I ，如图1所示：∵四边形ABCD 是正方形， ∴AB ＝BC ，∠AEI ＝∠ABC ＝90°， ∴∠BAC ＝45°， ∴∠AIE ＝∠BAC ＝45°，∴AE＝EI，∵AE＝CF，∴CF＝EI，∵EI∥BC，∴∠EIG＝∠FCG，∠IEG＝∠CFG，在△EIG和△FCG中，EIG FCG EI FCIEG CFG ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△EIG≌△FCG（ASA），∴EG＝FG，∴G是EF的中点；②在Rt△AEI中，∠AEI＝90°，AE＝EI，∴△AEI是等腰直角三角形，∴AI，∴AI AE∵EI∥BC，∴AIAE＝ICEB∴IC，∵△EIG≌△FCG，∴IG＝CG＝12IC，∴CG＝12＝2BE；（2）解：BE和CG之间的数量关系为：BE；理由如下：过点E作EI∥BC交AC于点I，如图2所示：∵四边形ABCD是矩形，∴∠AEI＝∠ABC＝90°，AB∥CD，AB＝CD，在Rt△AEI和Rt△ABC中，∠ABC＝∠AEI＝90°，AB＝2BC，∴tan∠IAE＝IEAE＝BCAB＝12，∴AE＝2IE，∵AE＝2CF，∴IE＝CF，∵EI∥BC，∴∠EIG＝∠FCG，∠IEG＝∠CFG，在△EIG和△FCG中，EIG FCG EI CFIEG CFG ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△EIG≌△FCG（ASA），∴EG＝FG，IG＝CG，设IE＝a，则AE＝2a，在Rt△AEI中，∠AEI＝90°，∴AI，cos∠IAE＝AEAI，即AEAI，∵EI∥BC，∴ICEB＝AIAE，∴ICEB，∵IG＝CG＝12IC，∴CG，∴BE；（3）解：作FP∥AB交AC于P，如图3所示：则FP∥CD，∠CFP＝∠ABC＝90°，∠CPF＝∠CAB，在Rt△CFP和Rt△ABC中，AB＝2BC，∴tan∠CPF＝CFPF＝tan∠CAB＝BCAB＝12，∴PF＝2CF，∵AE＝2CF，∴AE＝PF＝2，同（2）得：△AEG≌△PFG（AAS），∴AG＝PG，∵BF＝2，CF＝1，∴BC＝3，CD＝AB＝2BC＝6，∴AC∵FP∥AB，∴△CPF∽△CAB，∴PCAC＝CFBC＝13，∴PC＝13AC PA＝AC﹣PC＝∴AG＝PG＝12PA ∵FP∥CD，∴△PFH∽△CDH，∴PHCH＝PFCD＝26＝13，∴PH＝14 PC∴GH＝PG+PH＝【点睛】本题是四边形综合题，主要考查了正方形的性质、矩形的性质、勾股定理、三角函数、全等三角形的判定与性质、平行线的性质、相似三角形的判定与性质等知识；作辅助线构建全等三角形与相似三角形是解题的关键．13．（2022·湖南常德·九年级校考期中）如图1，ΔABC中，AB=AC，点D在BA的延长线上，点E在BC上，DE=DC，点F是DE与AC的交点．（1）求证：∠BDE=∠ACD；（2）若DE=2DF，过点E作EG//AC交AB于点G，求证：AB=2AG；（3）将“点D在BA的延长线上，点E在BC上”改为“点D在AB上，点E在CB的延长线上”，“点F是DE 与AC的交点”改为“点F是ED的延长线与AC的交点”，其它条件不变，如图2．①求证：AB·BE=AD·BC；②若DE=4DF，请直接写出SΔABC:SΔDEC的值．【答案】（1）见解析；（2）见解析；（3）①见解析；②16:15．【分析】（1）运用等腰三角形的性质及三角形的外角性质就可解决问题．（2）如图1，证明△DCA≌△EDG（AAS），得AD=EG，根据等腰三角形的判定得：DG=AB，由平行线分线段成比例定理得：2DE DGDF AD==，由此可得结论；（3）①如图2△DCA≌△EDG（AAS），得DA=EG，再证明△ACB∽△GEB，列比例式可得结论；②如图3，作辅助线，构建△ABC和△DCE的高线，先得14AF ADEG DG==，设AF=a，则EG=AD=4a，DG=16a，根据AH∥PD，得123164PD BD aAH AB a===，设PD=3h，AH=4h，根据EG∥AC，同理得41164BG BE aAB BC a===，设BE=y，BC=4y，利用三角形面积公式代入可得结论．【详解】（1）证明：∵AC=AB，∴∠ACB=∠B，∵DC=DE，∴∠DCE=∠DEC，∴∠ACD+∠ACB=∠B+∠BDE，∴∠BDE=∠ACD；（2）证明：如图1，∵EG∥AC，∴∠DAC=∠DGE，∠BEG=∠ACB，由（1）知：∠DCA=∠BDE，∵DC=DE，∴△DCA≌△EDG（AAS），∴AD=EG，∵∠B=∠ACB=∠BEG，∴EG=BG=AD，∴DG=AB，∵DE=2DF，AF∥EG，∴2 DE DGDF AD==，∴DG=2AD=2AG，∴AB=DG=2AG；（3）解：①如图2，过点E作EG∥AC，交AB的延长线于点G，则有∠A=∠G，∵AB=AC，CD=DE，∴∠ACB=∠ABC，∠DCE=∠DEC，∴∠ACD+∠DCE=∠EDG+∠DEC，∴∠ACD=∠EDG，在△DCA和△EDG中，∵ACD EDGA GCD DE∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DCA≌△EDG（AAS）．∴DA=EG，∵AC∥EG，∴△ACB∽△GEB，∴AC BC EG BE=，∵EG=AD，AC=AB，∴AB•BE=AD•BC；②如图3，过A作AH⊥BC于H，过D作DP⊥BC于P，则AH∥PD，∵AF∥EG，∴AF AD DF EG DG DE==，∵DE=4DF，∴14 AF ADEG DG==，设AF=a，则EG=AD=4a，DG=16a，∵∠ACB=∠ABC，∴∠GBE=∠BEG，∴BG=EG=4a，∴BD=12a，∵AH∥PD，∴123164 PD BD aAH AB a===，设PD=3h，AH=4h，∵EG∥AC，∴41164 BG BE aAB BC a===，设BE=y，BC=4y，∴S△ABC=12BC•AH=4•42y h=162yh=8yh，S△DCE=12CE•PD=5•32y h=152yh，∴S△ABC：S△DEC=8yh：152yh=16：15．【点睛】本题是三角形的综合题，考查了相似三角形的判定与性质、全等三角形的判定与性质、平行线分线段成比例、等腰三角形的性质和判定等知识，第三问有难度，利用参数表示各线段的长是本题的关键，综合性较强．，将BCP沿直线【答案】(1)见解析(2)或2 5(3)13或3或555【分析】（1）由四边形ABCD 是平行四边形得到AD BC ∥，则E CBE =∠∠，由折叠可知，EBF CBE ∠=∠，则E EBF ∠=∠，即可得到结论；（2）过点B 作BM AE ⊥于点M ，分点F 在点D 的右侧和点F 在点D 的左侧两种情况进行求解即可；（3）分五种情况，分别画出图形，分别进行求解即可．【详解】（1）证明：∵四边形ABCD 是平行四边形，∴AD BC ∥，∴E CBE =∠∠，由折叠可知，EBF CBE ∠=∠，∴E EBF ∠=∠，∴BF EF =；（2）过点B 作BM AE ⊥于点M ，则3tan 4BM A AM ==，设3,4BM x AM x ==，且0x >，∵10AB =，四边形ABCD 为菱形，∴10AB BC CD AD ====，在Rt ABM 中，222AM BM AB +=，即()()2224310x x +=，解得2x =，∴6,8BM AM ==，∴1082DM AD AM =−=−=，当点F 在点D 的右侧时，如图，。

相似三角形优秀教案相似三角形教案相似三角形教案(好)一、知识概述(一)相似三角形1、对应角相等，对应边成比例的两个三角形，叫做相似三角形．温馨提示：①当且仅当一个三角形的三个角与另一个(或几个)三角形的三个角对应相等，且三条对应边的比相等时，这两个(或几个)三角形叫做相似三角形，即定义中的两个条件，缺一不可；②相似三角形的特征：形状一样，但大小不一定相等；③相似三角形的定义，可得相似三角形的基本性质：对应角相等，对应边成比例，其应用广泛．2、相似三角形对应边的比叫做相似比．温馨提示：①全等三角形一定是相似三角形，其相似比k=1．所以全等三角形是相似三角形的特例．其区别在于全等要求对应边相等，而相似要求对应边成比例．②相似比具有顺序性．例如△ABC∽△A′B′C′的对应边的比，即相似比为k，则△A′B′C′∽△ABC的相似比，当且仅当它们全等时，才有k=k′=1．③相似比是一个重要概念，后继学习时出现的频率较高，其实质它是将一个图形放大或缩小的倍数，这一点借助相似三角形可观察得出．3、如果两个边数相同的多边形的对应角相等，对应边成比例，那么这两个多边形叫做相似多边形．4、相似三角形的预备定理：如果一条直线平行于三角形的一条边，且这条直线与原三角形的两条边(或其延长线)分别相交，那么所构成的三角形与原三角形相似．温馨提示：①定理的基本图形有三种情况，如图其符号语言：∵DE∥BC，∴△ABC∽△ADE；②这个定理是用相似三角形定义推导出来的三角形相似的判定定理．它不但本身有着广泛的应用，同时也是证明下节相似三角形三个判定定理的基础，故把它称为“预备定理”；③有了预备定理后，在解题时不但要想到上一节“见平行，想比例”，还要想到“见平行，想相似”．(二)相似三角形的判定1、相似三角形的判定：判定定理(1)：两角对应相等，两三角形相似．判定定理(2)：两边对应成比例且夹角相等，两三角形相似．判定定理(3)：三边对应成比例，两三角形相似．温馨提示：①有平行线时，用上节学习的预备定理；②已有一对对应角相等(包括隐含的公共角或对顶角)时，可考虑利用判定定理1或判定定理2；③已有两边对应成比例时，可考虑利用判定定理2或判定定理3．但是，在选择利用判定定理2时，一对对应角相等必须是成比例两边的夹角对应相等． 2、直角三角形相似的判定：斜边和一条直角边对应成比例，两直角三角形相似．温馨提示：①由于直角三角形有一个角为直角，因此，在判定两个直角三角形相似时，只需再找一对对应角相等，用判定定理1，或两条直角边对应成比例，用判定定理2，一般不用判定定理3判定两个直角三角形相似；②如图是一个十分重要的相似三角形的基本图形，图中的三角形，可称为“母子相似三角形”，其应用较为广泛．③如图，可简单记为：在Rt△ABC中，CD⊥AB，则△ABC∽△CBD∽△ACD．(三)三角形的重心1、三角形三条中线的交点叫做三角形的重心．2、三角形的重心与顶点的距离等于它与对边中点的距离的两倍．二、重点难点疑点突破1、寻找相似三角形对应元素的方法与技巧正确寻找相似三角形的对应元素是分析与解决相似三角形问题的一项基本功．通常有以下几种方法：(1)相似三角形有公共角或对顶角时，公共角或对顶角是最明显的对应角；相似三角形中最大的角(或最小的角)一定是对应角；相似三角形中，一对相等的角是对应角，对应角所对的边是对应边，对应角的夹边是对应边；(2)相似三角形中，一对最长的边(或最短的边)一定是对应边；对应边所对的角是对应角；对应边所夹的角是对应角．2、常见的相似三角形的基本图形：学习三角形相似的判定，要与三角形全等的判定相比较，把证明三角形全等的思想方法迁移到相似三角形中来；对一些出现频率较高的图形，要善于归纳和记忆；对相似三角形的判定思路要善于总结，形成一整套完整的判定方法．如：(1)“平行线型”相似三角形，基本图形见上节图．“见平行，想相似”是解这类题的基本思路；(2)“相交线型”相似三角形，如上图．其中各图中都有一个公共角或对顶角．“见一对等角，找另一对等角或夹等角的两边成比例”是解这类题的基本思路；(3)“旋转型”相似三角形，如图．若图中∠1=∠2，∠B=∠D(或∠C=∠E)，则△ADE∽△ABC，该图可看成把第一个图中的△AD E绕点A旋转某一角度而形成的．温馨提示：从基本图形入手能较顺利地找到解决问题的思路和方法，能帮助我们尽快地找到添加的辅助线．以上“平行线型”是常见的，这类相似三角形的对应元素有较明显的顺序，“相交线型”识图较困难，解题时要注意从复杂图形中分解或添加辅助线构造出基本图形．三、解题方法技巧点拨1、寻找相似三角形的个数例1、(吉林)将两块完全相同的等腰直角三角形摆成如图的样子，假设图形中所有点、线都在同一平面内，回答下列问题：(1)图中共有多少个三角形？把它们一一写出来；(2)图中有相似(不包括全等)三角形吗？如果有，就把它们一一写出来．分析：(1)在△ABC内，有五个三角形，加上△ABC与△AFG，共有七个三角形．(2)这是依据相似三角形判定定理来解决的计数问题．由于“不包括全等”，图中还剩五个非直角三角形，考虑到题设中两个三角形摆放的随意性，∠1不一定等于∠2，而∠B=∠C=45°，∠3、∠4都为钝角，又排除△ABD与△ACE相似，还剩三个三角形，这三个三角形相似．解：(1)共有七个三角形，它们是△ABD、△ABE、△ADE、△ADC、△AEC、△ABC 与△AFG．(2)有相似三角形，它们是△ABE∽△DAE，△DAE∽△DCA，△ABE∽△DCA(或△ABE∽△DAE∽△DCA)．点拨：①解决这类计数问题，一定要依据图形与定理，全面、周密思考，做到不重不漏，这类题有利于发散思维的培养和创新意识的形成；②有兴趣的同学可继续探索一下本题中BD、DE、EC三条线段有何关系？2、画符合要求的相似三角形例2、(上海)在大小为4×4的正方形方格中，△ABC的顶点A、B、C在单位正方形的顶点上，请在图中画出一个△A1B1C1，使得△A1B1C1∽△ABC(相似比不为1)，且点A1、B1、C1都在单位正方形的顶点上．（1）（2）分析：设单位正方形的边长为1，则△ABC的三边为，从而根据相似三角形判定定理2或3可画△A1B1C1，易得点拨：在4×4的正方形方格中，满足题设的△A1B1C1只能画出以上三个，若正方形方格数不加限制，则和△ABC相似且不全等的三角形可以画无数个．3、相似三角形的判定例3、(1)如图，O是△ABC内任一点，D、E、F分别是OA、OB、OC的中点，求证：△DEF∽△ABC；(2)如图，正方形ABCD中，E是BC的中点，DF=3CF，写出图中所有相似三角形，并证明．分析：(1)根据题设，观察图形易见，DE、EF、FD分别是△AOB、△BOC、△COA的中位线，利用三角形的中位线性质可证△DEF与△ABC的三边对应成比例；(2)由于正方形的四条边相等，且BE=CE，DF=3CF，设出正方形边长后，图中所有线段都能求出，故可从三边是否成比例判定哪些三角形相似．点拨：①第(1)题，若点O在△ABC外，其他条件不变，结论仍成立；②第(2)题也可用判定定理2，先证△ABE∽△ECF，得出∠AEF=90°后，再证其中任意三角形与△AEF相似，显然，以上证法较简便．4、直角三角形相似的判定例4、求证：若一个直角三角形的一条直角边和斜边上的高与另一个直角三角形的一条直角边和斜边上的高成比例，那么这两个直角三角形相似．已知：如图，Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，CD、C′D′分别是两个三角形斜边上的高，且CD︰C′D′=AC︰A′C′．求证：△ABC∽△A′B′C′．分析：判定直角三角形相似的方法除使用一般三角形的判定方法外，还可使用“斜边和一直角边对应成比例的两直角三角形相似”这一定理．证明△ABC∽△A′B′C′，只要再证一锐角对应相等即可．证明：∵CD、C′D′分别是△ABC、△A′B′C′的高，∴△ACD、△A′C′D′是直角三角形．5、三角形重心问题例5、已知△ABC的重心G到BC边上的距离为5，那么BC边上的高为()A．5 B．12C．10 D．15解析：因为G为△ABC的重心，所以DG︰DA=1︰3，因为GE⊥BC，AF⊥BC，所以GE∥AF，所以GE︰AF=DG︰DA=1︰3，因为GE=5，所以AF=15．6、相似三角形的综合运用例6、如图，CD是Rt△ABC斜边AB上的中线，过点D垂直于AB的直线交BC于E，交AC延长线于F．求证：(1)△ADF∽△EDB；(2)CD2=DE·DF．分析：(1)△ADF与△EDB都是直角三角形，要证它们相似，只要再找一个角对应相等即可；(2)注意到CD是斜边AB的中线，AD=BD=CD，由结论(1)不难得出结论(2)．证明：(1)∵DF⊥AB，∴∠ADF=∠BDE=90°，又∵∠F＋∠A=∠B＋∠A，∴∠F=∠B，∴△ADF∽△EDB．(2)由(1)得，∴AD·BD=DE·DF．又∵CD是Rt△ABC斜边上的中线，∴AD=BD=CD．故CD2=DE·DF．点拨：本题综合考查了直角三角形的性质与相似三角形的判定等．这是一道阶梯型问题，第(2)题根据(1)得出有关比例式，然后使用“等线代换”使问题简捷获证．其实第(2)题也可这样思考：把它转化为比例式，证明这三条线段所在的△CDE∽△FDC．请同学们完成这一证明．例7、如图，AD是△ABC的角平分线，BE⊥AD于E，CF⊥AD于F．求证：．分析：待证式中的四条线段不是在两个三角形中，无法直接根据两个三角形相似得出，需要插入一个“中间比”，由题设易证△ABE∽△ACF，△BDE∽△CDF，从中不难找到这个中间比．证明：∵AD是△ABC的角平分线，∴∠1=∠2．∵BE⊥AD，CF⊥AD，∴∠3=∠4=90°，∴△ABE∽△ACF，点拨：①当无法直接由两个三角形相似得出结论中的比例式时，一般可寻找“中间比”帮忙；例8、如图，在正方形ABCD中，M、N分别是AB、BC上的点，BM=BN，BP⊥MC 于点P．求证：(1)△PBN∽△PCD；(2)PN⊥PD．分析：要证PN⊥PD，即证∠DPN=90°，由已知∠BPC=90°，而∠BPC与∠DPN有公共部分∠CPN，因此只要证明∠4=∠5即可．这就必须先证明出结论(1)．在△PBN 与△PCD中，易证∠1=∠3，以下只要证明夹∠1、∠3的两边对应成比例．证明：(1)在正方形ABCD中，AB∥CD，∠ABC=90°．∵BP⊥MC，∴△PBM∽△PCB．点拨：要注意观察出图中存在的“母子相似三角形”基本图形，从而充分利用它得出∠1=∠2及△PBM∽△PCB等重要结论相似三角形教案相似三角形教案①回忆两个三角形相似的概念，巩固两个三角形相似的性质与判定。