当前位置：文档之家 › 飞行器结构力学 王生楠 受剪板式薄壁结构内力和位移计算

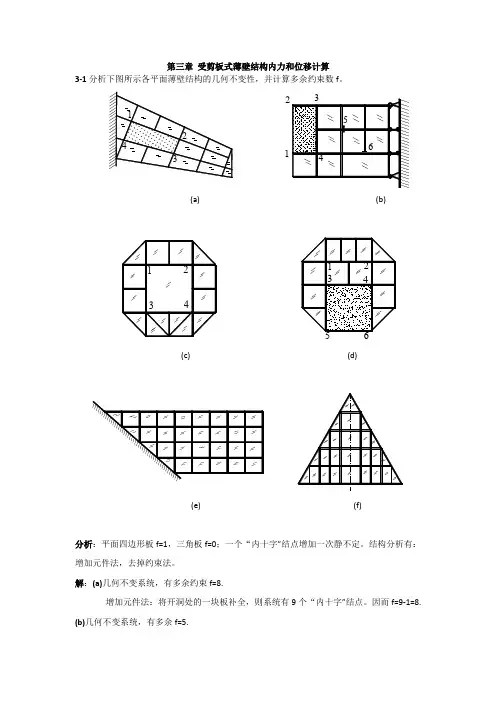
飞行器结构力学 王生楠 受剪板式薄壁结构内力和位移计算

  • 格式：pdf
  • 大小：1.72 MB
  • 文档页数：54

下载文档原格式

  / 54

合集下载

飞机结构力学_第6章

飞机结构力学_第6章


F tyds M x

F

txds

M
y

F tds N z

假定组成该薄壁结构的各元件的材料相同，则剖面上各点 的正应力为
z = Ax + By + C
6.2.1 理论推导
薄壁梁受复合载荷时的剖面正应力计算公式（坐标轴xoy 为剖面任意形心坐标轴）：
6.1 工程梁理论基本假设 6.2 自由弯曲时正应力的计算 6.3 自由弯曲时开剖面的剪流 6.4 开剖面弯心的计算 6.5 自由弯曲时单闭室剖面剪应力的计算 6.6 多闭室剖面剪流与弯心的近似计算
剪流的大小
图示结构为一个剖面周线为任意的不闭合形状，且沿纵向 不变的开剖面薄壁梁。在横向载荷作用下，纵向任意剖面 上的内力为Qy、Mx和Qx、My等。假设整个剖面都能承受 正应力。
推导开剖面剪流计算公式时，没有明确剪力Qx和Qy的作 用点，但明确了剪力与剪流的合力应相平衡。
由于开剖面的弯曲剪流的分布规律只取决于剖面的几何性 质Sx及Sy，故剖面上剪流合力作用点也就由剖面几何特性 决定，而与载荷Qx、Qy无关。
对于一个开剖面薄壁结构来说，剖面上存在着一个由其几 何特性决定其位置的点，即自由弯曲时，剖面剪流合力的 作用点——弯心（剪心、扭心、刚心）。
剪流的大小
N z 0 z
M x z
Qy
M y z

Qx
1
q Jx
s 0
1 k (Qy
Qx
J xy Jy
) ytds

1 Jy
s 0
1 k (Qx
Qy
J xy Jx
) xtds
飞行器结构力学 王生楠 第三章 受剪板式薄壁结构内力和位移计算

飞行器结构力学 王生楠 第三章 受剪板式薄壁结构内力和位移计算


取 2-3 杆 N 32 qb Pb / c ； 取 1-6 杆 N 61 Pb / c
验证结构剩余局部 3-6 杆的平衡，满足。 内力图：
P
q=P/c Pb/c
P Pb/c P
q=P/c
P
(d)静定结构。 零力杆端：
N 32 0, N 34 0, N 29 0, N 94 0, N 98 0, N 69 0, N 54 0, N 56 0, N 89 0, N 78 0, N 69 0
分析总体平衡得 N12 P, N 76 P . 对称结构，受对称载荷，内力具有对称性。 取 4-9 杆 ，
q P/a；
取 3-4 杆， N 43 qb Pb / a ；
取 2-3 杆， N 23 qa P ；
取 1-2 杆， q12 0 ； 取 2-9 杆， N 29 qb Pb / a
取总体平衡
M
6
0 ，得 N1 2
2 P， 2
取结点 2
得 N 27
P P ， N 2 3 2 2
取杆 3-2，有 q0
P 2a P 2
取杆 6-3，有 N 63
校核总体平衡，满足。 内力图：
P 0.5P
q0
P 2a
0.5P
2 P 2
0.5P
(f)静定结构。 零力杆端:
段结构静不定次数为 7； 七个四缘条盒段双边连接结构静不定次数为 7×3； 再加两根杆和一 个四边形板，三个约束。因而 f=1+7+7×3+3=32. (o) 几何不变系统，多余约束数 f=31. 一个自由的单层端框有 10 个结点的空心笼式结构为静定结构； 三个单端固定的单层端 框有 10 个结点的空心笼式结构静不定次数为 3×（10-3） ；增加元件法：将开洞处的板补全 后为依次连接两个单端固定的单层端框有 9 个结点的空心笼式结构静不定次数 2×（ （9-3） -1）.因而 f=31. 3-3 平面薄壁结构的形状、尺寸及受载情况如下图所示。求各元件内力并作内力图。
飞行器结构力学电子教案7-1

飞行器结构力学电子教案7-1


飞机薄壁结构典型元件受力分析及其理想化 ▄ 飞机薄壁结构典型元件受力分析及其理想化 （1）蒙皮 ）
在结构作为一个整体的受力和传力过程中， 在结构作为一个整体的受力和传力过程中，蒙皮的主要作用是支承和传递由于剪切 和扭转而引起的剪应力，同时它还部分支承和传递由于弯曲而引起的正应力。正应力 和扭转而引起的剪应力，同时它还部分支承和传递由于弯曲而引起的正应力。 主要由较强的长桁和突缘等纵向元件承担，蒙皮在这方面的作用是第二位的。因此， 主要由较强的长桁和突缘等纵向元件承担，蒙皮在这方面的作用是第二位的。因此， 在对蒙皮进行理想化的时候，假设蒙皮只承受并传递剪应力； 在对蒙皮进行理想化的时候，假设蒙皮只承受并传递剪应力；蒙皮实际上具有的承受 并传递正应力的能力将人为地附加到纵向元件（如长桁）上去。 并传递正应力的能力将人为地附加到纵向元件（如长桁）上去。 由于蒙皮壁厚一般很薄，可近似认为蒙 由于蒙皮壁厚一般很薄， 皮上的剪应力大小沿厚度方向不变化， 皮上的剪应力大小沿厚度方向不变化，且 剪应力沿厚度中线的切线方向。 剪应力沿厚度中线的切线方向。因为剪应 力的值沿厚度方向不变， 力的值沿厚度方向不变，所以可以用剪应 力沿厚度方向的合力 q = τ ×t 来替代剪应 为剪流， 力，称 q为剪流，用半箭头表示。 为剪流 用半箭头表示。
（2）组成骨架的杆子只承受轴向力；镶在骨架上的板（蒙皮）四边只受剪切， ）组成骨架的杆子只承受轴向力；镶在骨架上的板（蒙皮）四边只受剪切， 即每块板与其周围的杆子之间只有剪力作用。 即每块板与其周围的杆子之间只有剪力作用。
▄ 受剪板式薄壁结构的计算模型
（3）板的厚度相对于长、宽等其它 ）板的厚度相对于长、 尺寸是很小的，可以认为板很薄。 尺寸是很小的，可以认为板很薄。因 此可近似认为板剖面上的剪应力τ 此可近似认为板剖面上的剪应力 沿厚 度不变（如图(a)示 度不变（如图 示）。
西工大飞行器结构力学电子教案1-1省公开课金奖全国赛课一等奖微课获奖PPT课件

西工大飞行器结构力学电子教案1-1省公开课金奖全国赛课一等奖微课获奖PPT课件

三、结构力学计算模型
第一章 绪论
刚接
刚接力学特征：
被连接元件在刚接点处，即不能 发生相对移动，也不能绕刚接点 发生相对转动。
所以，刚接即能够传递力，也能 够传递力矩。
夹角保持不变
将刚性连接处涂黑来表示刚接，
也称为刚结点。
19/38
飞行器结构力学基础
三、结构力学计算模型
第一章 绪论
组合结点
组合结点力学特征：
37/38
飞行器结构力学基础
六、基本关系和基本假设
第一章 绪论
2. 基本假设
（1）小变形假设
结构在外载荷作用下变形与几何尺寸 相比很小。建立力平衡方程时，能够 不考虑变形对结构几何关系影响。
（2）线弹性假设
结构在载荷作用下会产生内力和变形， 当载荷卸调后，内力和变形也随之消 失，结构恢复到原始状态，无残余变 形(弹性体)。
平面定向支座
36/38
飞行器结构力学基础
六、基本关系和基本假设
第一章 绪论
1. 基本关系
（1）平衡关系
作用在结构上力是平衡，结构系统中 全部元件也是平衡。
（2）协调关系 结构发生变形时，各个元件之间变形
是协调。
（3）物理关系 元件力和位移之间，满足材料物理性
质。
结构力学原理和计算方法均是基于这三种基本关系而 建立。
固定支座（或称固持） 定向支座
21/38
飞行器结构力学基础
三、结构力学计算模型
第一章 绪论
可动铰支座
可动铰支座几何特征：
结构含有绕铰A转动及平行 于基础平面方向平动，但在 垂直于基础平面方向上不能 发生平动。 相当于限制了结构一个平动。
22/38
飞行器结构力学基础
飞行器结构力学讲义

飞行器结构力学讲义

飞行器结构力学郑晓亚王焘西北工业大学2011年6月目录第一章绪论 (1)1.1 结构力学在力学中的地位 (1)1.2 结构力学的研究内容 (1)1.3 结构力学的计算模型 (1)1.4 基本关系和基本假设 (3)第二章结构的组成分析 (5)2.1 几何可变系统和几何不变系统 (5)2.2 自由度、约束和几何不变性的分析 (5)2.3 组成几何不变系统的基本规则、瞬变系统的概念 (7)2.4 静定结构和静不定结构 (12)第三章静定结构的内力及弹性位移 (13)3.1 引言 (13)3.2 静定桁架的内力 (13)3.3 静定刚架的内力＊ (16)3.4 杆板式薄壁结构计算模型 (19)3.5 杆板式薄壁结构元件的平衡 (20)3.6 静定薄壁结构及其内力 (25)3.7 静定系统的主要特征 (34)3.8 静定结构的弹性位移 (35)第四章静不定结构的内力及弹性位移 (45)4.1 静不定系统的特性 (45)4.2 静不定系统的解法——力法 (45)4.3 对称系统的简化计算 (54)4.4 静不定系统的位移 (57)4.5 力法的一般原理和基本系统的选取 (60)第五章薄壁梁的弯曲和扭转 (64)5.1 引言 (64)5.2 自由弯曲时的正应力 (65)5.3 自由弯曲时开剖面剪流的计算 (68)5.4 开剖面的弯心 (71)5.5 单闭室剖面剪流的计算 (77)I5.6 单闭室剖面薄壁梁的扭角 (81)5.7 单闭室剖面的弯心 (82)5.8 多闭室剖面剪流的计算＊ (86)5.9 限制扭转的概念＊ (91)第六章结构的稳定 (94)6.1 引言 (94)6.2 压杆的稳定性 (95)6.3 薄板压曲的基本微分方程 (95)6.4 薄板的临界载荷 (99)6.5 板在比例极限以外的临界应力 (102)6.6 薄壁杆的局部失稳和总体失稳 (103)6.7 加劲板受压失稳后的工作情况——有效宽度概念 (104)6.8 加劲板受剪失稳后的工作情况——张力场梁概念 (108)II第一章绪论1.1 结构力学在力学中的地位结构力学是飞行器结构计算的理论基础。

计算固体计算力学-第二章非线性方程组的解法解答

计算固体计算力学-第二章非线性方程组的解法解答

15
计算固体计算力学
Newton法得到的序列{an}具有二阶收敛速度。 粗略的说，用Newton法迭代一次大约有效数位 增加一倍，例如， a0准确到一位，则迭代3次就 可以得到准确8位的近似解。这意味着Newton 法收敛很快，这是它的主要优点。
Newton法自校正的。也就是说，an+1仅依赖于 Ψ(an)及an，前面迭代产生的舍入误差不会一步步 传下去。
am+1=am+Δam 在以上各式中，下标m表示增量步的步数， 而λm=1的解对应于Ψ(a)=P(a)-R=0的解。
34
计算固体计算力学
在一个自变量的情况下，求解非线性方程 组的过程如下图所示。如果Δλm足够小，则认 为所得解即为方程组的合理的近似解。
但是，在计算的每一步，都会引起某些偏 差，结果使解答漂移，而且随着求解步数的 增多，这种偏差不断积累，以致 最后的解将偏离真解较远。
31
计算固体计算力学
2.4 增量方法
求解非线性方程组的另一类方法是增量方法。 使用这种方法需要知道“荷载”项(R)为零时问 题的解(a)0。在实际问题中，(R)经常代表真实 荷载，(a)0 代表结构位移。在问题的初始状态， 它们均为零。这种从问题的初值开始，随着荷 载列阵(R)按增量形式逐渐增大，研究(a)i的变 化规律的方法，称为增量方法。
Kn
1

an
,


K
n1
an1 an

a n 1

an
,
K n1 K n K n
n 0,1, 2,
其中，ΔKn是Kn的一个低秩修正矩阵，常 用的是秩1或秩2的矩阵，以减小计算量。
ΔKn的选取查阅相关的资料。
结构力学(王生楠)西工大出版 课后题答案第四章_力法

结构力学(王生楠)西工大出版 课后题答案第四章_力法


P
P
P
1
P
(b)
(b)解：对称结构，在反对称载荷作用下，在对称轴上对称的内力为零。受力分析如图所示
有 2 根对称轴，结合平衡方程，剩下三个未知数，为 3 次静不定。 本题中通过对称性条件的使用，将 6 次静不定问题转化为 3 次静不定。
(c) (c)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。
(
)
N13 = P + X 1 ⋅ 1 =
(182 2⎞ 1− 9 2 ⎟=− P + X1 ⋅ ⎜ − P ⎜ 2 ⎟ 2 18 ⎝ ⎠
N 24 = 0 + X 1 ⋅ 1 = −
5+ 2 P 23
N34 = −
4、校核。 结点 2： 结点 3：
⎛ 2 2 ⎞ 1− 9 2 ⎟ P + X1 ⋅ ⎜ − ⎜ 2 ⎟ = 18 P 2 ⎝ ⎠
3
4 -2 √3 1 2 <1>
a
3
2 <P>
计算影响系数
∆1 P =
a ⎡ 2 ⎤ Pa 3P × (− 2 ) + (− 2 P )× 3 × =− 4+ 2 3 ⎢ ⎥ EA ⎣ EA 3⎦
(
)
δ11 =
列正则方程：
a ⎛ 2 ⎞ a + 1× 1× 2 ⎟ = 6+2 3 ⎜2× 2 + 3× 3 × EA ⎝ 3 ⎠ EA
(
)
N13 = 2 P + X 1 ⋅1 =
(2 + 2 ) P
4
⎛ 2 ⎞ 3− 2 ⎟ N14 = 0 + X 1 ⋅ ⎜ P ⎜− 2 ⎟ = 4 ⎝ ⎠ ⎛ 2 ⎞ 3− 2 ⎟ N 23 = 0 + X 1 ⋅ ⎜ − P ⎜ 2 ⎟= 4 ⎝ ⎠
飞行器结构力学电子教案5-2

飞行器结构力学电子教案5-2


θ1
12 8L3 6 − 2 4L 12 8L3 6 − 2 4L − 6 4L2 2 2L 6 − 2 4L 4 2L v2
θ2
v3
θ3
消除总刚奇异性。 (4) 引入位移边界： v1 = v 3 = 0 ，消除总刚奇异性。 引入位移边界：
4 L 6 − 2 EJ L 2 L 0
e
k13 k23 k33 k43 k53 k625 k35 k45 k55 k65
k16 k26 k36 k46 k56 k66
Ui Vi Mi Uj Vj Mj
[Kii ] [Kij ] K = [K ji ] [K jj ]
位移法
Displacement Method of Structure Analysis 第二讲 梁元素与刚架的位移法求解
5.3 平面梁元素与平面刚架位移法求解
一、梁元素在局部坐标系中的平衡方程及刚度矩阵 在元素局部坐标系中， 在元素局部坐标系中， 长度为L，结点编号为i 长度为 ，结点编号为 j 的平面梁元素如图所 示，梁的截面拉伸刚 度为EA， 度为 ，截面抗弯刚 度为EJ 度为 。因为梁元素 记梁元素在局部坐标系中的结点位移 能承受轴向力、 能承受轴向力、横向 列阵和结点力列阵分别为： 列阵和结点力列阵分别为： 剪力和弯矩， 剪力和弯矩，故梁的 {δ }e = ui vi θ i u j v j θ j 每个结点上有三个位 移分量， 移分量，相应的也有 {F }e = U i Vi M i U j V j M j 三个结点力。 三个结点力。
EA L 0 0 [ K ]e = EA − L 0 0
0 12 EJ L3 6 EJ L2 0 12 EJ − 3 L 6 EJ L2
飞行器结构力学电子教案73PPT课件

飞行器结构力学电子教案73PPT课件

设每个端框上有 n 个结点，两个端框共有 2n个结点。 系统的自由度数为 N ＝ 2n×3 ＝ 6n 。 每一个端框的约束数为 2n －3； 纵向有 n 根杆和 n 块板，约束数为 2n； 系统全部的约束数为 C ＝ 2(2n-3) + 2n + 6。
则：f ＝C－N ＝ 6n－6n ＝ 0 ，满足几何不变的必要条件。
飞行器结构力学基础
——电子教学教案
航空结构工程系
1
第七章
受剪板式薄壁结构内力和位移 计算
第三讲 7.4 静定空间薄壁结构内力计算
2
一、空间薄壁结构的组成分析
组成薄壁结构的各元件的中心点和中线不都在同一平面内，则称为空间薄 壁结构，它可以承受任意方向的外载荷。3Leabharlann 一、空间薄壁结构的组成分析
在研究空间薄壁结构的组成规律时，仍把结点看成为自由体，每个空间结 点具有3个自由度；把杆和板看成为约束，杆和四边形板均起1个约束作用。
f ＝ 28
13
二、静定空间薄壁结构的内力计算
1、分析静不定度。 2、判断零力杆端，假设剪流方向。 3、利用结点法求杆端轴力，或由杆的平衡求剪流或另一端杆轴力。 4、绘制内力图。
零力杆端的判断：
三根不共面的杆交于无 载荷作用的点，则此三根 在该端处的轴力均为零。
14
【例1】 求图示空间薄壁结构的内力。已知：L＝100mm，B＝40mm， H＝10mm，P 1＝200N，P 2＝300N，P 3＝500N。
N84(q2q3)L4000 N73(q4q2)L4000
3、绘制力图。
4、校核。
X0 Mx 0 Y 0 My 0
Z 0 Mz 0
16
【例2】计算图示结构的内力。已知四缘条双层自由盒段，在两层交界5点处 将缘条切断，在杆子的切口处有大小相等方向相反的一对单位力。 解： 1、5点被切开，相当于去掉一个约束， 故该结构是静定的。 2、假定1-2-6-5和5-6-10-9两板的剪流 分别为q1和q2，其方向如图(b) 所示， 5-6-7-8板的剪流为q3，其方向如图(c) 所示。先判断零力杆端，再按平衡条 件确定各板剪流之间的关系。
《飞行器结构力学基础》课程教学大纲

《飞行器结构力学基础》课程教学大纲

《飞行器结构力学基础》课程教学大纲一、课程基本信息1、课程代码：（0120140）2、课程名称（中/英文）：飞行器结构力学基础/Structural Mechanics for Aerocraft3、学时/学分：50/6.54、先修课程：理论力学、结构强度基础、弹性力学， /0120120/01201705、面向对象：飞行器设计与工程专业本科生6、开课院（系）：航空学院（航空结构工程系）7、教材、教学参考书：《结构力学基础》, 黄其青，王生楠，西北工业大学出版社，2001.4《飞行器结构力学》,王生楠，西北工业大学出版社,1998.12二、课程性质和任务《飞行器结构力学基础》是航空高等院校飞行器结构设计和结构强度专业教学计划中的一门专业技术基础课，是航空飞行器设计、固体力学、流体力学、工程力学、理论与应用力学、人机环境与工程等学科或专业的必修课程。

本课程以杆系和薄壁结构为对象，研究杆系和薄壁结构的组成原理及其受力和变形分析的力法和位移法，薄壁工程梁理论，结构分析中的能量原理。

通过本课程的学习，使学生了解和掌握结构的受力和传力特点、薄壁工程梁和能量原理的基本理论和基本计算方法，培养学生对结构设计和强度计算的概念和综合处理能力，培养从事飞行器结构设计和强度计算的高技术人才。

三、教学内容和基本要求第一章绪论 2学时1.1 结构力学的研究对象和任务；1.2结构力学的计算模型简化；1.3结构的外载荷、内力和支反力；1.4 基本关系和基本假设。

第二章结构几何组成分析 4学时2.1 结构的几何特性；2.2 自由度和约束; 2.3 几何特性分析的运动学方法;2.4 几何特性分析的静力学方法; 2.5 几何不变系统的组成规则; 2.6 瞬变系统的判别方法。

第三章静定杆系结构的内力和变形计算 6学时3.1 桁架的组成，桁架的计算模型，桁架几何不变性分析，静定桁架内力计算（结点法、剖面法和混合法）; 3.2 刚架的组成，刚架的计算模型，刚架几何不变性分析，静定刚架内力计算，混合杆系结构的内力计算; 3.3 元件的应变能，虚功原理，单位载荷法，静定杆系结构的位移计算。

飞行器结构力学电子教案7-2

飞行器结构力学电子教案7-2

飞行器结构力学基础
——电子教学教案
航空结构工程系
第七章
受剪板式薄壁结构内力和位移 计算
第二讲 7.3 静定平面薄壁结构内力计算
一、平面薄壁结构的组成分析
受剪板式薄壁结构的计算模型是由结点、杆和板元件组成。如果这些元件 的中心点和中线都在同一平面内，则称为平面薄壁结构，它只能承受作用在 此平面内的外载荷。
解： 1、组成分析。
q1
q3
内“十”字结点被切断，结构为静定系统。
2、求内力。
q2
q4
判断零力杆端，如图所示。
根据受力情况，假设各板的剪流方向如图 所示。
由1-4-7杆的平衡： q1 q2
由3-6-9杆的平衡： q3 q4
由4-5杆的平衡： q1 q2 0 由5-6杆的平衡： q3 q4 P / a
P h2
梯形板的平均剪流为：
q
q23
h2 h1
P h1
取梯形板为分离体，可求出其它边的剪流：
q41
q h2 h1
Ph2 h12
由1－2杆的平衡：
由3－4杆的平衡：
N12
q
l
cos
P h1
l
cos
N 43
q
l
cos
P h1
l
cos
3、验证：取整个结构为分离体，检查内力
计算结果是否满足平衡条件：
2
1
“三边连接”
f ＝ 1＋2＝3 增加两个静不定度。
一、平面薄壁结构的组成分析
其他分析方法：增减元件法。
对于飞机结构上常见的环形薄壁框结构，内部有“开口”，可用简便方法 分析其组成。
增加元件法。假想将中间的开口用板补起来，此时结构有四个内结点，所 以有4个多余约束，因中间的板实际上是不存在的，减去一个约束。因此原 结构实际上有3个多余约束。即 f ＝ 3。 去掉约束法。假想去掉二杆和一块四边形板，此时的结构是没有内“十” 字结点的静定结构。因原结构实际上多了三个元件，故原结构是具有3个多 余约束的静不定结构，即 f ＝ 3。

毕业设计 飞机机翼单壁室剖面薄壁梁的程序计算

1.2 研究思路以及方法
本文是将只受剪力的飞机机翼剖面，简化成对称的单闭室剖面薄壁结构，继而用
图1.1
C语言编程，实现机翼受力后剪流的计算，使复杂的计算变得极为简单方便。即将蒙
皮简化成不承担正应力的薄壁结构，将桁条、翼梁、墙简化成缘条，再把整个简化模型用C语言编程，通过计算，获得简化结构在只承受剪力作用时，整个剖面所受剪流的大小。（如图1.1）
E.板每一个边上的剪流沿着长度不变（即剪流为常量）。这样，板的每一个边上就只有一个未知剪流。
采用上述简化假设的受剪板式薄壁结构计算模型，只包含两类结构元件，即承受轴力的杆和承受剪流的板，杆与板之间只有剪流作用。
根据上述简化假设得到的薄壁结构计算模型为受剪板式薄壁结构计算模型，是航空结构中常用的计算模型。实践证明，这种模型的计算结果一般能满足工程的要求。
图1.2
1.3 本文研究特色
将只受剪力的飞机机翼剖面，简化成对称的单闭室剖面薄壁结构，进而用C语言编程，实现飞机机翼剪流的快速计算，节省计算时间，提高计算准确度。
本文将复杂的计算简便化，在程序运行时，通过输入剪力的大小及其作用位置、缘条的个数以及各个缘条的坐标和横截面积，就可以计算出开口时的剪流、开口处的剪流、总剪流等数据。（如图1.3）
而随着近些年航空业的飞跃式发展，飞机在设计过程中对安全性、效率性的要求不断提高，简单的人力计算已经无法保证庞大计算的准确与效率，这就要求把飞机各个部分的计算模块化，进而用计算机计算代替人力计算，使飞机在设计校核过程中的复杂计算更快、更准确的进行，以便研制出高性能的飞机，适应实际需求。
1.1.2研究意义
1）三角形板
将一块三角形板与周边杆件分开，取做分离体，用未知剪流q代替杆件对它的作用。由于受剪板式计算模型中，杆与板之间只有剪流作用，而且板每一边得剪流为一常量，所以可以用三个剪流 、 、 来表示三角形板的受力情况，如图（3.1）.剪流 的下标表示板对杆作用的剪流是由i点指向j点，因此杆对

西北工业大学(王生楠)结构力学课后题答案第五章位移法


2 − 2 0 −4 0 0 0 0 − 2 4+ 2 0
4 0 0 8+ 2 0 − 2 0 −4 0 0 0 0
0 − 2 −4 4+ 2 0 0 8+ 2 0 − 2 0 −4
⎤ ⎥ ⎥ − 2 ⎥ ⎥ 2 ⎥ 0 ⎥ ⎥ 0 ⎥ ⎥ 0 ⎥ 0 ⎥ ⎥ −4 ⎥ 0 ⎥ ⎥ 4 + 2⎦ ⎥ 0 0
K 1− 4
⎡ 1 3 −1 − 3⎤ ⎢ ⎥ 3 3 − 3 −3 ⎥ 3 EA ⎢ = 8l ⎢ − 1 − 3 1 3 ⎥ ⎢ ⎥ 3 3 ⎥ ⎢− 3 − 3 ⎣ ⎦
�
杆元 1-5，长度为 2l , θ = 30 , λ = cos θ =
3
2
, µ = sin θ = 1 . 2
K 1−5
2
4
6
60°
7
1 a
3 a
5 a
(b)
解：以节点 1 为原点，建立如图所示的总体坐标系。 建立元素刚度矩阵。杆元 1-3， l = a, θ = 0 , λ = cos θ = 1, µ = sin θ = 0.
�
K 1−3
⎡1 ⎢0 EA ⎢ = a ⎢− 1 ⎢ ⎣0
0 −1 0 0 0 1 0 0
0 0⎤ 0 − 1⎥ ⎥ 0 0⎥ ⎥ 0 1⎦
杆元 1-5，长度为 2l
θ = 60 � , λ = cos θ = 1 , µ = sin θ = 3 , 2 2 3,
K 1−5
⎡ 1 3 −1 − 3⎤ ⎢ ⎥ 3 3 − 3 −3 ⎥ 3 EA ⎢ = 8l ⎢ − 1 − 3 1 3 ⎥ ⎢ ⎥ 3 3 ⎥ ⎢− 3 − 3 ⎣ ⎦
K 1− 2

南京航空航天大学飞行器 结构力学 课后习题答案 第2章

第二章薄板的弯曲2-1 写出2-1图所示矩形薄板的边界条件。

OA为简支边，并作用有分布的弯矩M。

BC边为固支边，OC边为简支边。

AB边为自由边。

Mx解：OA边：wx00；2w2w2wD(2u2)D2x yx0xMx0x0MyOC边：wy00；y02w2w2wD(2u2)D2y xy0yy0BC边：wx a0；wxx aAB边：Myy b2w2w D(2u2)0y xy b Myx x)y b(Qy3w3w D[3(2u)2]0y x yy b2-2 如图2-2所示，矩形薄板OA边和OC边为简支边，AB和BC为自由边，在点B受向下的横向集中力P。

试证w mxy可作为该薄板的解答，并确定常数m、D(2u2)＝0y xy0OA边上：wx02w2w0；D(2u2)＝0x yx02w2w3w3w0；D[3(2u)2]0 AB边上：D(2u2)y xy b y x yy b2w2w3w3w0；D[3(2u)]0 BC边上：D(2u2)x yx a x x y2x a2w)2D(1u)m P 在B点上：2D(1u)(x yx a,y bm P 2D(1u)所以w Pxy 2D(1u)2w2w2w2wMx D(2u2)0；My D(2u2)0；y x x yMxy2wP D(1u)；Qy D2w0 Qx D2w0；x y2y x2wRA2D(1u)()P RC；RO P x yA2-3 有一矩形薄板，边长为a和b。

若其挠度函数为w=Cxy(a-x)(b-y)，求该薄板受什么样的载荷和边界的支持条件。

解：w Cxy(a x)(b y)Cabxy Caxy2Cbx2y Cx2y2 w Caby Cay22Cbxy2Cxy2；xw Cabx2Caxy Cbx22Cx2y；y2w2w222Cax2Cx2Cby2Cy；；22y x4w4w4w4C；40；40 x2y2x x由4w q/D24C q/D q8CDx0时：wx00；w x0不是固支边，是简支边x0(Mx)x02w D2x2CD(y2by)Mxx0x a时：wx a0；w x0不是固支边，是简支边x a(Mx)x a2w D2xwy2CDy(b y)Mx x ay0时：wy00；0不是固支边，是简支边y0(My)y02w D2y2CDx(a x)Myy0y b时：wy b0；w y0不是固支边，是简支边y b(My)y b2w D2y2CDx(a x)Myy b2-5 四边简支正方形薄板，边长为a，在板中点受横向载荷P，试求最大挠度。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 受剪板式薄壁结构内力和位移计算 3-1 分析下图所示各平面薄壁结构的几何不变性，并计算多余约束数 f。
1
2 4
3
23 5
6
1
4
(a)
(b)
1
2
3
4
(c)
1
2
3
4
5
6
(d)
(e)
(f)
分析：平面四边形板 f=1，三角板 f=0；一个“内十字”结点增加一次静不定。结构分析有： 增加元件法，去掉约束法。 解：(a)几何不变系统，有多余约束 f=8.
有 12 个“内十字”结点。因而 f=12. 3-2 分析下图所示空间薄壁结构的几何不变性，并计算多余约束数 f。
2 1
3 4
2 1
3
4 5 6
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
1 6
5
2 3
4
(i)
(j)
1
2
6
3
5
4
8
7 6
1 2 3 4
5
(k)
(l)
1
8
2
7
65
(m)
(n)
(o) 分析：三缘条盒段若以四边形面与基础连接则有 1 次静不定（进行结构分析：视结点 为自由体有 3 个自由度，板和杆各自起一个约束作用），若以三边与基础相连则为无多余约 束的静定结构；对于一端固定的一段空心薄壁结构，端框有 n 个结点，其静不定次数为(n-3), 故单边连接的四缘条盒段有 1 次静不定；对于四缘条盒段若以相邻两面和基础相连则由结构 分析可知有 3 次静不定；对于三缘条盒段若以一边为三角形另一边为四边形和基础相连则由 结构分析可知有 2 次静不定，若以双边四边形形式连接三缘条盒段则静不定次数为 3。 解：(a)几何不变系统，多余约束数 f=4。 增加元件法：将开洞处的板 1-2-3-4 补全，为 5 个单边连接的四缘条盒段。因而 f=5-1=4。 (b)几何不变系统，多余约束数 f=3. 增加元件法：将开洞处的板 1-2-5-6、2-3-4-5 补全，依次为一个三缘条盒段以四边形面 与基础连接有 1 次静不定和四个四缘条盒段单边连接有 1 次静不定。因而 f=1+4-2=3. (c) 几何不变系统，多余约束数 f=4. 一个单边连接四缘条盒段，一个双边连接四缘条盒段。因而 f=1+3=4.
(d) 几何不变系统，多余约束数 f=3. 一个单边连接三缘条盒段，一个双边连接四缘条盒段。因而 f=3. (e) 几何不变系统，多余约束数 f=8. 一个单边连接三缘条盒段，两个双边连接四缘条盒段，一个双边连接三缘条盒段。因 而 f=2×3+2=8. (f) 几何不变系统，多余约束数 f=2. 进行结构分析，短的四缘条盒段与基础为单边连接静不定次数为 1，在此基础上增加了 4 个结点，5 个板，8 根杆。因而 f=1+5+8-4×3=2. (g) 几何不变系统，多余约束数 f=2. 以自由短四缘条盒段为基础，静定结构；以四边形形式单边连接三缘条盒段，静不定 次数为 1；单边连接四缘条盒段，静不定次数为 1。因而 f=1+1=2. (h) 几何不变系统，多余约束数 f=10. 以四边形形式单边连接三缘条盒段，静不定次数为 1；连个双边连接的四缘条盒段，静 不定次数为 2×3；双边四边形形式连接三缘条盒段，静不定次数为 3。因而 f=1+2×3+3=10. (i) 几何不变系统，多余约束数 f=2. 两个以单边四边形方式连接的三缘条盒段。f=2×1=2. (j) 几何不变系统，多余约束数 f=5. 单层端框有六个结点的有一个隔框笼式结构静不定次数为 1；单端固定的单层端框有六 个结点的有一个隔框笼式结构静不定次数为（6-3+1）.因而 f=1+（6-3+1）=5。 (k) 几何不变系统，多余约束数 f=3. 单端固定的单层端框有六个结点的空心笼式结构静不定次数为（6-3）。因而 f=3. (l) 几何不变系统，多余约束数 f=14. 为两个单端固定的单层端框有八个结点的有两个隔框笼式结构静不定次数 2× （8-3+2）.因而 f=14. (m) 几何不变系统，多余约束数 f=7. 单端固定的单层端框有八个结点的空心笼式结构静不定次数 （8-3）；增加元件法：将 开洞处的板补全后为单端固定的单层端框有六个结点的空心笼式结构静不定次数 （（6-3） -1）。因而 f=7. (n) 几何不变系统，多余约束数 f=32. 一个三缘条盒段以四边形面与基础连接结构静不定次数为 1；七个单边连接的四缘条盒
P
1
2
4
3
b
1
c
P 2
c 2
3
4
c
(a)
(b)
bb
a
bbc)
2
2P
3
4
12
3
2P
8
9
4
7 a 6a 5
(d)
5
a
6 P7
1
4
3
2
a
a
a
(e)
P
a 1
P
a
2
3
2P
8
5
4
2P
7
6
(f)
1
2
a
段结构静不定次数为 7；七个四缘条盒段双边连接结构静不定次数为 7×3；再加两根杆和一 个四边形板，三个约束。因而 f=1+7+7×3+3=32.
(o) 几何不变系统，多余约束数 f=31. 一个自由的单层端框有 10 个结点的空心笼式结构为静定结构；三个单端固定的单层端 框有 10 个结点的空心笼式结构静不定次数为 3×（10-3）；增加元件法：将开洞处的板补全 后为依次连接两个单端固定的单层端框有 9 个结点的空心笼式结构静不定次数 2×（（9-3） -1）.因而 f=31. 3-3 平面薄壁结构的形状、尺寸及受载情况如下图所示。求各元件内力并作内力图。
增加元件法：将开洞处的一块板补全，则系统有 9 个“内十字”结点。因而 f=9-1=8. (b)几何不变系统，有多余 f=5.
增加元件法：将开洞处的一块板补全，切开端口杆的杆端处连上，则系统有 4 个“内 十字”结点，外部多余约束数为 3，对于端口切开的杆：丁字节点 6 处为零力杆端切开与否 对静不定次数无影响，而处于“内十字”结点处的 5 处，则解除一次静不定。因而 f=4+3-1-1=5. (c)几何不变系统，有多余约束 f=4.
有 4 个“内十字”结点。因而 f=4. (d) 几何不变系统，有多余约束 f=3.
增加元件法：将开洞处的一块板补全，则系统有 4 个“内十字”结点。因而 f=4-1=3. (e)几何不变系统，有多余约束 f=21.
有 21 个“内十字”结点。因而 f=21. (f) 几何不变系统，有多余约束 f=12.