专题六 第4讲 推理证明、算法初步、复数

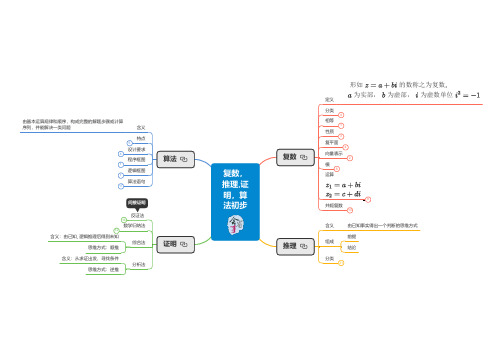
《推理与证明、数系的扩充与复数》zdj18()()()⎧⎪⎪⎨⎪⎪⎩1归纳推理：由某类事物的部分对象具有某些特征推出该类事物的全部对象具有这些特征的推理，合情 或者由个别事实概括出一般结论的推理，即归纳推理是由部分到整体，由个别到一般的推理； 2类比推理：由两类对象具有某些类似特征和其中一类对象的某些已知特征，推出另一类对象也推理 具有这些特征的推理，即类比推理是由特殊到特殊的推理；1定义：从一般性的原理出发，推出某个特殊情况下演绎推理推理与证明()()()⎧⎪⎧⎪⎪⎨⎨⎪⎪⎪⎩⎩ 的结论，即演绎推理是由一般到特殊的推理；大前提：已知的一般原理；2三段论模式小前提：所研究的特殊情况；结论：根据一般原理，对特殊情况作出判断；1综合法：一般地，利用已知条件和某些数学定义、公理、定理等，经过一系列的推理论证，最 后推导出所要证明的结论成立；2分析法：一般地，从要证明的结论出发，逐步寻求使它成立的充分条件，直至最后，把要证明 证明方法()()()()()()000,1n n n n N n k k n k N n k ++⊗∈⊗=≥∈=+ 的结论归结为判定一个明显成立的条件已知条件、定理、定义、公理等为止；3反证法：一般地，假设原命题不成立即在原命题的条件下，结论不成立，经过正确的推理， 最后得出矛盾，因此说明假设错误，从而证明了原命题成立；应用范围：证明一个与正整数有关的命题；归纳奠基：证明当取第一个值时命题成立；数学步4归纳推理：假设时命题成立，证明当归纳法骤()()02112n n i i ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎧⎪⎪⎪⎪⎧⎪⎪⎪⎪⎨⎪⎨⎪⎪⎪⎪⎪⎪⎪⊗⎩⎩⎪⎪⎪⎩⎪⊕⎪⎪⎪⎩=-时命题也成立；总结：完成以上两步，就可断定命题对从开始的所有正整数都成立；由合情推理所获得的结论仅仅是一种猜想，未必可靠；演绎推理在大前提、小前提和推理形式都正确 的前提下，得出的结论一定正确；；虚数单位的性质实数可以与之进行四则运算，进复数()(,)(,),0a bi a b R z a bi a b R a b a bi b z a bi b ⎧⎪⎨⎪⎩+∈=+∈+⎫⎧⎫⎧⎪⎪⎪⎪⎨⎬⎛⎫⎪⎪⎪⎪ ⎪⎪⎪=⎩⎨⎬⎭⎝⎭⎪⎪⎫⎧⎪⎪⎨⎬=+⎪⎪⎩⎭⎩⎭行四则运算时，原有的加、乘运算律仍然成立；复数的概念：形如的数叫复数，记作，其中分别叫复数的实部与虚部；循环小数正有理数有理数零整数、有限小数、负有理数无限循环小数实数小数复数正无理数复数的分类：无理数无限不循环小数负无理数虚数()()()()()()()()()()()()00000(,,,)(,),()()a b a b a bi c di a b c d R a c b d z a bi a b R a b a bi c di a c b d i a bi c di ac bd bc ad i a b a bi c di ⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎧=≠⎪≠⎪⎨≠≠⎪⎪⎩⎩+=+∈⇔===+∈←−−−−→+±+=±+±++=-++++÷+=一一对应纯虚数且非纯虚数且复数相等的条件：且；复数的几何意义：复数复平面内的点Z ；加减法：；复数乘 法：；运算法则除 法：()()()()()()()()()441424322330111310111,256n n n n i c di c di i i ii i i i x x z z z R ωωωωωωωωω+++⎧⎪⎪⎨⎪+≠⎪+⎩⎧===-=-⎪⎪=-++====⎪⎨⎪=⇔∈⎪⎪⎩；1任意两个虚数不能比较大小； 2的周期性：；；；；结的性质：若=； ；； 4若，则或； 论； 在复数集中，实系数一元二次方程都有解；7共轭复数：两个复数的实部相等、虚部互为相反数；1题型()⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎨⎪⎪⎩⎩确定复数何时为纯虚数或实数问题：利用复数分类处理；2复数范围内方程根的问题：利用复数相等的条件处理；。

2012二轮专题六：概率与统计、推理与证明、算法初步、复数第四讲 推理与证明【考纲透析】1．合情推理与演绎推理（1）了解合情推理的含义，能利用归纳和类比等进行简单的推理，了解合情推理在数学发现中的作用；（2）了解演绎推理的重要性，掌握演绎推理的基本模式，并能运用它们进行一些简单推理；（3）了解合情推理和演绎推理之间的联系和差异。

2．直接证明与间接证明（1）了解直接证明的两种基本方法——分析法和综合法；了解分析法和综合法的思考过程、特点； （2）了解间接证明的一种基本方法——反证法；了解反证法的思考过程、特点。

3．数学归纳法了解数学归纳法的原理，能用数学归纳法证明一些简单的数学命题。

【要点突破】要点考向1：合情推理考情聚焦：1．合情推理能够考查学生的观察、分析、比较、联想的能力，在高考中越来越受到重视； 2．呈现方式金榜经，属中档题。

考向链接：1．归纳推理是由部分到整体，由个别到一般的推理，在进行归纳时，要先根据已知的部分个体，把它们适当变形，找出它们之间的联系，从而归纳出一般结论；2．类比推理是由特殊到特殊的推理，是两类类似的对象之间的推理，其中一个对象具有某个性质，则另一个对象也具有类似的性质。

在进行类比时，要充分考虑已知对象性质的推理过程，然后类比推导类比对象的性质。

例1：（2010·福建高考文科·Ｔ１６）观察下列等式： ① cos2a=22cos a -1;② cos4a=84cos a - 82cos a + 1;③ cos6a=326cos a - 484cos a + 182cos a - 1;④ cos8a=1288cos a - 2566cos a + 1604cos a - 322cos a + 1;⑤ cos10a= m 10cos a - 12808cos a + 11206cos a + n 4cos a + p 2cos a - 1. 可以推测，m – n + p = .【命题立意】本题主要考查利用合情推理的方法对系数进行猜测求解． 【思路点拨】根据归纳推理可得．【规范解答】观察得：式子中所有项的系数和为1，m 12801120n p 11∴-+++-=，m n p 162∴++=，又9p 10550,m 2512=⨯===，n 400∴=-，m n p 962∴-+=． 【答案】962．要点考向2：演绎推理考情聚焦：1．近几年高考，证明题逐渐升温，而其证明主要是通过演绎推理来进行的；2．主要以解答题的形式呈现，属中、高档题。

所谓的光芒光阴，其实不是此后，闪烁的日子，而是无人问津时，你对梦想的偏执第 4 讲数学概括法【 2013 年高考会这样考】1．数学概括法的原理及其步骤．2．能用数学概括法证明一些简单的数学命题．【复习指导】复习时要抓住数学概括法证明命题的原理，清晰其内在的联系，掌握数学概括法证明命题的一般步骤，熟知每一步之间的差别联系，熟习数学概括法在证明命题中的应用技巧．基础梳理1．概括法由一系列有限的特别案例得出一般结论的推理方法，往常叫做概括法．依据推理过程中考察的对象是波及事物的全体或部分可分为完整概括法和不完整概括法．2．数学概括法(1) 数学概括法：设{ P n} 是一个与正整数有关的命题会合，假如：①证明开端命题P1(或 P0)成立；②在假定P k建立的前提下，推出P k＋1也建立，那么能够判定{ P n} 对全部正整数建立．(2)用数学概括法证明一个与正整数有关的命题时，其步骤为：①概括奠定：证明当取第一个自然数n0时命题建立；*②概括递推：假定n＝ k，( k∈N， k≥n0)时，命题建立，证明当n＝k＋1时，命题建立；两个防备数学概括法是一种只合用于与正整数有关的命题的证明方法，第一步是递推的“基础”，第二步是递推的“依照”，两个步骤缺一不行，在证明过程中要防备以下两点：(1)第一步考证 n＝ n0时， n0不必定为1，要依据题目要求选择适合的开端值．(2) 第二步中，概括假定起着“已知条件”的作用，在证明n＝k＋1时，命题也建立的过程中必定要用到它，不然就不是数学概括法．第二步要点是“一凑假定，二凑结论”．三个注意运用数学概括法应注意以下三点：(1)n＝n0时建立，要弄清楚命题的含义．(2) 由假定n＝k建立证n＝k＋ 1 时，要推导详确，而且必定要运用n＝ k 建立的结论．(3) 要注意n＝k到n＝k＋1 时增添的项数．双基自测1．在用数学法明凸n 形的角21n( n－3)条，第一步第一个n0等于() ．A． 1B．2C．3D．0分析数最少的凸n 形是三角形．答案C2．利用数学法明不等式1＋1＋1＋⋯＋ n 1＜(n)(≥2，∈ N* ) 的程，由n＝k到23 2 － 1f n n＝＋1，左增添了 () ．n kA．1B． k C． 2k－1D．2k111111111k 分析1＋2＋3＋⋯＋2k＋1－1－1＋2＋3＋⋯＋2k－ 1＝2k＋2k＋1＋⋯＋2k＋ 1－1，共增添了2，故 D.答案D2n＋11－a n＋2*3．用数学法明：“ 1＋a＋a＋⋯＋ a＝1－a ( a≠1，n∈N ) ”在n＝ 1，左端算所得的 () ．A． 1B． 1＋aC． 1＋a＋a2D． 1＋a＋a2＋a3答案C4．某个命与自然数n 有关，若 n＝ k( k∈N*)命建立，那么可推适合n＝ k＋1命也建立，已知 n＝5，命不建立，那么能够推得() ．A．n＝6 命不建立B．n＝ 6 命建立C．n＝4 命不建立D．n＝ 4 命建立分析法一*n＝k＋1命也建立．因此若n＝4建立，由 n＝ k( k∈N )建立，可推适合必有 n＝5建立．知 n＝5不建立，因此n＝4必定不建立．法二其逆否命“若当＝＋ 1 命不建立，当＝k 也不建立” 真，故“n＝5n k n不建立” ?“n＝4不建立”．答案C111135．用数学法明不等式n＋1＋n＋2＋⋯＋n＋n＞24的程中，由 n＝k 推 n＝ k＋1，不等式的左增添的式子是________．1111解析不等式的左增加的式子是2k＋1＋2k＋2－k＋1＝2k＋ 12k＋ 2，故填1.2k＋12k＋2答案12 ＋ 12 ＋ 2k k考向一 用数学 法 明等式【例 1】?用数学 法 明：tan α·tan 2 α ＋ tan 2 α·tan 3α ＋⋯＋ tan( n － 1) α·tann α ＝tann α － n ( n ∈ N * ，tan αn ≥2) ．[ 点 ]注意第一步 的 ，在第二步推理 明 要注意把假 作 已知．明tan 2 α － 2＝2－ 2＝2tan 2α＝ tan α·tan 2 α＝左(1) 当 n ＝2 ，右 ＝α22tan1－tan α 1－ tan α，等式建立．(2) 假 当 n ＝ k ( k ∈ N * 且 k ≥2) ，等式建立，即tan α·tan 2α＋ tan 2 α·tan 3α＋⋯＋ tan( k － 1) α·tank α＝tank α－ k ，tan α那么当 n ＝ k ＋ 1 ，tan α·tan 2α＋ tan 2 α ·tan 3α＋⋯＋ tan( k － 1) α·tank α ＋ tan k α ·tan( k ＋ 1) αtan k α＝ tanα － k ＋tank α ·tan( k ＋1) αtan k αk α ·tan( k ＋1) α－ ( k ＋1)＝ tanα ＋ 1＋tantan k α tan k ＋ 1α－ tan k α ＝tan α ＋tan[k ＋ 1 α－ k α]－ ( k ＋1)tankα＋ 1－ ( k ＋ 1) ．＝tan α就是 ，当n ＝k ＋ 1 等式也建立．由 (1)(2) 知， 任何 n ∈ N * 且 n ≥2，原等式建立．用数学 法 明等式 ，要注意第 (1) 步中 n 的 ，如本 要取 n ＝ 2，在第(2) 步的 明中 在 假 的基 上正确地使用正切的差角公式．【 1】 用数学 法 明：随意的 n ∈ N * ， 1 ＋1 ＋⋯＋2n － 11＝ n .1×3 3×5 2n ＋ 1 2n ＋ 1明(1) 当 n ＝1，左 ＝11 1 1 ＝ ，右＝ ，左 ＝右 ，因此等式建立．1×3 3 2×1＋ 13(2) 假 当 n ＝ k ( k ∈ N * 且 k ≥1) 等式建立，即有1＋1＋⋯＋12k＋ 1＝k ，1×3 3×52k－ 12k＋ 1当 n＝k＋1，1＋1＋⋯＋12k＋ 1＋12k＋ 31×3 3×52k－ 12k＋1 k12＋3 ＋1k＝2k＋ 1＋2k＋12k＋ 3＝2k＋ 12k＋ 32k2＋ 3k＋ 1k＋1＝k＋1，＝2k＋ 3＝k＋12k＋ 12k＋ 3 2＋ 1因此当 n＝ k＋1，等式也建立．由 (1)(2) 可知，全部∈N*等式都建立．n考向二用数学法明整除【例 2】?能否存在正整数m使得f ( n) ＝(2 n＋7) ·3n＋ 9 随意自然数n 都能被 m整除，若存在，求出最大的m的，并明你的；若不存在，明原因．[ 点 ]察所函数式，凑出推理要明所需的．解由 f ( n)＝(2 n＋7)·3n＋9得， f (1)＝36，f (2)＝3×36， f (3)＝10×36， f (4)＝34×36，由此猜想： m＝36.下边用数学法明：(1)当 n＝1，然建立；(2)假 n＝ k( k∈N*且 k≥1)， f ( k)能被36整除，即 f ( k)＝(2 k＋7)·3k＋9能被36整除；当 n＝ k＋1，[2( k＋1)＋7]·3k＋1＋9＝(2 k＋7)·3k＋1＋27－27＋2·3k＋1＋9＝3[(2 k＋7)·3k＋ 9] ＋18(3k －1－1) ，因为 3k－1－ 1是 2 的倍数，故18(3 k－1－ 1) 能被 36 整除，就是，当n＝ k＋1， f ( n)也能被 36 整除．由 (1)(2) 可知全部正整数n 都有f(n) ＝(2＋7) ·3n＋9 能被 36 整除，的最大 36.n m明整除的关“凑”，而采纳增、减、拆和因式分解等手段，凑出n＝ k 的情况，进而利用假使．【 2】用数学法明a n＋1＋( a＋1)2n－1( n∈N*)能被 a2＋a＋1整除．明(1) 当n＝1 ，a2＋ ( a＋ 1) ＝a2＋a＋ 1 可被a2＋a＋ 1 整除．(2)假 n＝ k( k∈N*且 k≥1)，a k＋1＋( a＋1)2k－1能被 a2＋ a＋1整除，当 n＝k＋1，a k＋2＋( a＋1)2k＋1＝a· a k＋1＋( a＋1)2( a＋1)2k－1＝ a·a k＋1＋a·(a＋1)2k－1＋( a2＋ a＋1)( a＋1)2k－1＝ a[ a k＋1＋( a＋1)2k－1]＋( a2＋ a＋1)(a＋1)2k－1，由假可知a[ a k＋1＋( a＋1)2k－1]能被 a2＋ a＋1整除， (2＋＋1)(＋1) 2k －1也能被2＋＋1 整除，∴ a k ＋2＋ ( a ＋ 1) 2 k ＋1 也能被 a 2＋ a ＋ 1 整除，即 n ＝ k ＋ 1 命 也建立，∴ 随意 n ∈ N * 原命 建立．考向三用数学 法 明不等式1【例 3】?用数学法明：全部大于 1的自然数，不等式 1＋31＋ 1·⋯· 1＋1 2n ＋ 15 2n － 1>2 均建立．[ 点 ] 本 用数学 法 明不等式，在推理 程顶用放 法，要注意放 的“度”．(1) 当 n ＝21 4 5明 ，左 ＝ 1＋ 3＝3；右 ＝ 2 .∵左 >右 ，∴不等式建立．(2) 假 n ＝ k ( k ≥2，且 k ∈ N * ) 不等式建立，1112k ＋ 1即 1＋3 1＋5 ·⋯· 1＋2 －1 >.k2当 n ＝k ＋ 1 ，1111＋ 211＋ 3 1＋ 5 ·⋯· 1＋ 2k － 1 k ＋ 1 －12k ＋ 1 2k ＋ 2 2k ＋ 2 4k 2＋ 8k ＋ 4 > 2 · ＝ ＝ 2 2k ＋ 12k ＋ 1 2 2k ＋ 14 2 ＋8 ＋32 ＋3 2 ＋ 12 k ＋1＋ 1>kk＝k k ＝.2 2k ＋ 122 2k ＋ 1∴当 n ＝k ＋ 1 ，不等式也建立．由 (1)(2) 知， 于全部大于1 的自然数，不等式都建立．n在由 n ＝ k 到 n ＝k ＋ 1 的推 程中， 用放 技巧，使 得以 化，用数学法 明不等式 ，从 n ＝ k 到 n ＝ k ＋ 1 的推 程中， 明不等式的常用方法有比 法、剖析法、 合法、放 法等．1 3n 1 n ＋1 n1【 3】 已知函数 f ( x ) ＝ 3x －x ，数列 { a } 足条件： a ≥1，a ≥ f ′(a ＋ 1)． 比1＋ a 1＋ 1 ＋ 1 11＋ a 2 ＋⋯＋ 与 1 的大小，并 明原因．1＋ a 3 1＋ a n解 ∵f ′(x ) ＝x 2 －1， a n ＋ 1≥ f ′(a n ＋1) ，∴ a n ＋ 1≥(a n ＋1) 2－ 1.∵函数( ) ＝ ( ＋1) 2 － 1＝x2＋ 2 在区 [1 ，＋∞ ) 上 增，于是由a 1≥1，得2≥( 1＋g xxxa a22322431) －1≥2－ 1， 而得a ≥(a ＋ 1) －1≥2－ 1＞ 2－ 1，n由此猜想： a n ≥2－ 1.下边用数学 法 明 个猜想：1①当 n ＝1 ， a 1≥2－ 1＝ 1， 建立；②假 ＝ ( ≥1且 k *建立，即ak＝ ＋1 ，由( ) ＝ ( x ＋1) 2∈N )≥2－1， 当n k k k g x－ 1 在区 [1 ，＋∞ ) 上 增知， a≥(a22kk ＋ 1，＋1) －1≥2 －1≥2－1，即 n ＝ k ＋ 1k ＋ 1k也建立．由①、②知， 随意n ∈ N * ，都有nn≥2－ 1.an1 1即 1＋ n ≥2，∴≤ n ，a1＋ a2n111111 111 n∴＋＋＋⋯＋≤＋2＋ 3＋⋯＋2 n ＝ 1－＜ 1.1＋ a1＋ a21＋ a1＋an 2 2 2213考向四、猜想、 明*【例 4】?数列 { a n } 足 S n ＝ 2n －a n ( n ∈ N ) ．(1) 算 a 1， a 2， a 3， a 4，并由此猜想通 公式 a n ；(2) 用数学 法 明 (1) 中的猜想．[ 点 ]利用n与a n的关系式求出 { n } 的前几 ，而后 出n，并用数学 法 明．S aa解 (1) 当 n ＝ 1 ， a 1＝ S 1＝2－ a 1，∴ a 1＝1.3当 n ＝ 2 ， a 1＋ a 2＝S 2＝2×2－ a 2，∴ a 2＝ 2.7当 n ＝ 3 ， a 1＋ a 2＋a 3＝ S 3＝2×3－ a 3，∴ a 3 ＝4.当 n ＝4 ，a1＋ 2＋ 3＋4＝ 4＝2×4－ 4，∴ 4＝15.aaaSaa 82n － 1*由此猜想 a n ＝ 2n － 1 ( n ∈ N) ．(2) 明①当 ＝ 1 ，左 ＝1＝ 1，右 ＝ 21－ 1＝ 1，左 ＝右 ， 建立． 0na 2*a ＝ 2 k － 1 ②假 n ＝ k( k ≥1且 k ∈ N ) ， 建立，即2k － 1 ，那么n ＝k ＋1 ，ka k ＋1 ＝S k ＋ 1－ S k ＝ 2( k ＋ 1) － a k ＋1 －2k ＋ a k ＝ 2＋ a k － a k ＋1，∴ 2a k ＋ 1＝ 2＋ a k ，2k － 1∴ a ＝ 2＋ k 2＋ 2k －1 ＝ 2k ＋ 1－ 12 ＝ 2 2 ，k ＋1ak表示 n ＝ k ＋ 1 ， 建立，2n － 1由①②知猜想 a n ＝ 2n － 1 建立．(1) 、猜想、 明是高考要点考 的内容之一，此 可分 性 和存在性 ，本例从特例下手，通 察、剖析、 、猜想，探究出一般 律．*(2) 数列是定在N 上的函数，与数学法所运用的范是一致的，而且数列的推公式与原理上是一致的，数列中有许多常用数学法解决．1【 4】由以下各式1＞2，1 11＋2＋3＞ 1，11111131＋＋＋＋＋＋＞，111＞ 2，1＋＋＋⋯＋231511151＋2＋3＋⋯＋31＞2，⋯，你能获得怎的一般不等式，并加以明．111n*答案猜想：第 n 个不等式1＋2＋3＋⋯＋2n－1＞2(n∈N )．1(1)当 n＝1，1＞，猜想正确．2(2)假当 n＝ k( k≥1且 k∈N*)猜想正确，1 11k即 1＋2＋3＋⋯＋2k－1＞2，那么，当 n＝ k＋1，1 11111k111k11 1＋2＋3＋⋯＋2k－1＋2k＋2k＋1＋⋯＋2k＋1－1＞2＋2k＋2k＋1＋⋯＋2k＋1－1＞2＋2k＋1＋2k＋1＋⋯＋1 k2k k1k＋1 k＋ 1＝＋ k ＋ 1＝＋＝.222222即当 n＝k＋1，不等式建立．∴ 于随意n∈N*，不等式恒建立．卷告20——因为方法不妥致失【断】用数学法明与正整数有关的一些等式命，关在于弄清等式两的组成律，等式的两各有多少，由n＝ k 到 n＝ k＋1，等式的两会增添多少，增添怎的，其点在于假后，怎样推下一个正整数命也建立.【防备举措】把假当成已知条件参加推理. 明确下一个正整数命建立的目，通适合的达到个目，里能够使用合法，也能够使用剖析法，甚至能够再次使用数学法.【示例】 ? 在数列 { a n } 、 { b n } 中， a 1＝ 2， b 1＝ 4，且 a n ， b n ， a n ＋ 1 成等差数列， b n ， a n ＋ 1，b n ＋ 1 成等比数列 ( n ∈ N * ) ．(1) 求 a 2 ，a 3， a 4 及 b 2， b 3， b 4，由此猜 { a n } ， { b n } 的通 公式，并 明你的 ；(2) 明：1 ＋1＋⋯＋15＋ 2＋b a＜ .11 2n＋ n12a ba b(1) 由条件得2 n ＝ n ＋2n n ＋ 1.n ＋ 1， n ＋ 1＝ba a ab b由此可得 a 2＝ 6， b 2＝9， a 3＝ 12， b 3＝ 16，a 4＝ 20， b 4＝ 25.2猜 a n ＝ n ( n ＋ 1) ， b n ＝ ( n ＋ 1) .用数学 法 明：①当 n ＝1 ，由上可得 建立．②假 当 n ＝ k ( k ≥1且 k ∈N *) ， 建立，即 a k ＝ k ( k ＋ 1) ， b k ＝( k ＋ 1) 2，2那么当 n ＝ k ＋ 1 ， a k ＋1＝ 2b k －a k ＝ 2( k ＋ 1) 2－ k ( k ＋1) ＝ ( k ＋ 1)( k ＋ 2) ，b k ＋ 1＝a k＋1＝ ( k ＋2) 2， b k因此当 n ＝ k ＋ 1 ， 也建立．由①②，可知a n ＝ n ( n ＋ 1) ，b n ＝ ( n ＋ 1) 2 全部正整数都建立．因第二 因为不等式的右端 常数， 自己是不可以用数学 法 明的，可考 用放法 明，也可考 加 不等式后，用数学 法 明．(2) 当 ＝1n11 511＝ ＜a ＋b 6 12假 n ＝k ( k ∈ N * ) 不等式建立1＋1＋⋯＋1 5即a ＋b ＋b ＜a ＋ b12ak1212 k当 n ＝ k ＋ 11＋1 ＋⋯＋ 1 ＋ 15 1a 1＋b 1 ＜ ＋ a k ＋ 1＋ b k ＋ 1a 2＋b 2 a k ＋ b k a k ＋ 1＋ b k ＋ 1 12 到此没法用数学 法 明．正解(1) 用 (1)(2) 明：11 5 . ＝ ＜a 1＋b 1 6 12n ≥2 ，由 (1) 知 a ＋ b ＝ ( n ＋ 1)(2 n ＋1) ＞ 2( n ＋ 1) n .nn故1＋ 1 ＋⋯＋1a 1a n ＋b n＋ b 1 a 2＋ b 21 1111＋＋⋯＋＜6＋2 2×3 3×4 n n ＋ 1＝1＋ 1 1 1 1 1 1 1 － ＋ －＋⋯＋ －1 111 1 15＝＋－＜＋＝.6 2 2n＋1 6 4 12。