下载文档原格式
运筹学论文——旅游路线最短问题摘要：随着社会的发展，人民的生活水平的提高，旅游逐渐成为一种时尚，越来越多的人喜欢旅游。
而如何才能最经济的旅游也成为人民考虑的一项重要环节，是选择旅游时间最短，旅游花费最少还是旅游路线最短等问题随之出现，如何决策成为一道难题。
然而，如果运用运筹学方法来解决这一系列的问题，那么这些问题就能迎刃而解。
本文以旅游路线最短问题为列，给出问题的解法，确定最短路线，实现优化问题。
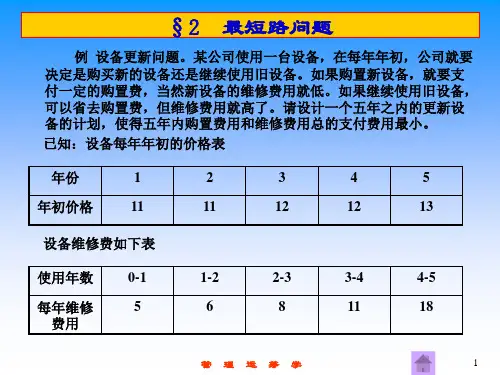
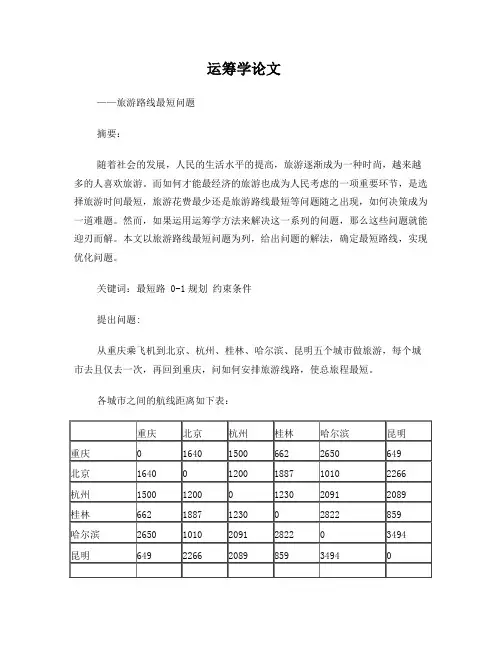
关键词：最短路 0-1规划约束条件提出问题:从重庆乘飞机到北京、杭州、桂林、哈尔滨、昆明五个城市做旅游，每个城市去且仅去一次，再回到重庆，问如何安排旅游线路，使总旅程最短。
各城市之间的航线距离如下表：问题分析：1．这是一个求路线最短的问题，题目给出了两两城市之间的距离，而在最短路线中,这些城市有的两个城市是直接相连接的（即紧接着先后到达的关系），有些城市之间就可能没有这种关系，所以给出的两两城市距离中有些在最后的最短路线距离计算中使用到了，有些则没有用。
这是一个0-1规划的问题，也是一个线性规划的问题。
2．由于每个城市去且仅去一次，最终肯定是形成一个圈的结构，这就导致了这六个城市其中有的两个城市是直接相连的，另外也有两个城市是不连接的。
这就可以考虑设0-1变量，如果两个城市紧接着去旅游的则为1，否则为0。
就如同下图3．因为每个城市只去一次，所以其中任何一个城市的必有且仅有一条进入路线和一条出去的路线。
LINGO解法：为了方便解题，给上面六个城市进行编号，如下表（因为重庆是起点，将其标为1）重庆北京杭州桂林哈尔滨昆明1 2 3 4 5 6假设：设变量x11。
如果x11=1,则表示城市i与城市j直接相连（即先后紧接到达关系），否则若x11=0，则表示城市i与城市j不相连。
特别说明：xij和xji是同一变量，都表示表示城市i与城市j是否有相连的关系。
这里取其中xij (i<j)的变量。
模型建立：由于这是一个最短路线的问题，且变量已经设好。
