运筹学——.图与网络分析-最短路
v2 (4) 5 v4
9
v6
4
1
v1 (0)
4
75
5
v8
① ②
64
v 3(6)
7 v 5 (8) 6
1
v7
③
④
4)接着往下考察,有四条路可走:(v2,v4), (v2,v5).
可选择的最短路为
(v3,v4), (v3,v5).
m k 2 , ik 4 2 n ,k 5 3 ,{ k 4 3 } 5m 9 ,8 , i 1 , n 1 } 0 { 3 8
(v5,v6), (v5,v7 ).
m k 2 ,i k 4 3 n ,k 4 5 ,k { 6 5 } 7 m 9 ,1 i ,1 n ,1 0 } 3 { 4 9
① 给(v2,v4) 划成粗线。
② 给 v 4 标号(9)。
③ 划第5个弧。
运筹学——.图与网络分析-最短路
v 2 ( 4 ) 5 v 4(9 ) 9 v 6 (13 )
运筹学——.图与网络分析-最短路
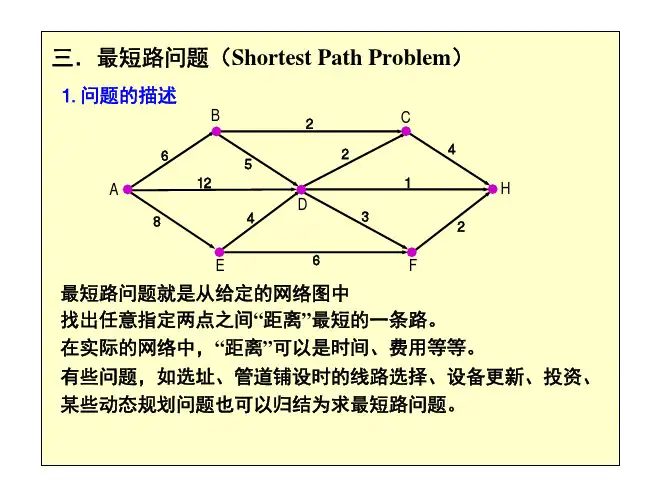
引言
随着科学技术的进步,特别是电子计算机 技术的发展,图论的理论获得了更进一步的发展, 应用更加广泛。如果将复杂的工程系统和管理问 题用图的理论加以描述,可以解决许多工程项目 和管理决策的最优问题。因此,图论越来越受到 工程技术人员和经营管理人员的重视。
运筹学——.图与网络分析-最短路
树图的各条边称为树枝假定各边均有权重一般图g2含有多个部分树其中树枝总长最小的部分树称为该图的最小部分树也称最小支撑树?定理1图中任一个点i若j是与i相邻点中距离最近的则边ij一定必含在该图的最小部分树内
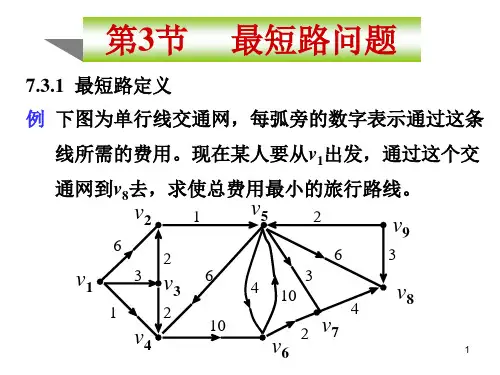
第6章 图与网络分析
本章内容重点 图的基本概念与基本定理 树和最小支撑树 最短路问题 网络最大流







![运筹学-最短路问题[课件参考]](https://uimg.taocdn.com/199eaa4c5727a5e9846a6140.webp)
