运筹学上机报告最短路问题的计算机求解
- 格式:doc
- 大小:40.50 KB
- 文档页数:3

最短路问题的求解方法最短路问题是图论中的一个经典问题,它在很多实际应用中都有着重要的作用。
在现实生活中,我们经常需要求解最短路径,比如在地图导航、网络通信、交通运输等领域。
因此,研究最短路问题的求解方法具有重要的理论意义和实际应用价值。
在图论中,最短路问题的求解方法有很多种,其中比较经典的有Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法等。
这些算法各有特点,适用于不同的场景和要求。
下面我们就逐一介绍这些算法的原理和求解方法。
Dijkstra算法是一种用于求解单源最短路径的算法,它采用贪心策略,每次找到当前距离最短的节点进行松弛操作,直到所有节点都被遍历。
Dijkstra算法的时间复杂度为O(V^2),其中V为节点的个数。
这种算法适用于边权值为正的图,可以求解从单个源点到其他所有点的最短路径。
Bellman-Ford算法是一种用于求解单源最短路径的算法,它可以处理边权值为负的图,并且可以检测负权回路。
Bellman-Ford算法的时间复杂度为O(VE),其中V为节点的个数,E为边的个数。
这种算法适用于一般情况下的最短路径求解,但是由于其时间复杂度较高,不适用于大规模图的求解。
Floyd-Warshall算法是一种用于求解所有点对最短路径的算法,它可以处理边权值为正或负的图,但是不能检测负权回路。
Floyd-Warshall算法的时间复杂度为O(V^3),其中V为节点的个数。
这种算法适用于求解图中所有点对之间的最短路径,可以同时求解多个源点到多个目标点的最短路径。
除了上述几种经典的最短路求解算法外,还有一些其他的方法,比如A算法、SPFA算法等。
这些算法在不同的场景和要求下有着各自的优势和局限性,需要根据具体情况进行选择和应用。
在实际应用中,最短路问题的求解方法需要根据具体的场景和要求进行选择,需要综合考虑图的规模、边权值的情况、时间效率等因素。
同时,对于大规模图的求解,还需要考虑算法的优化和并行化问题,以提高求解效率。


最短路问题的求解方法最短路问题是图论中一个经典的问题,它在实际生活中有着广泛的应用,比如在交通规划、网络通信、物流配送等领域都有着重要的作用。
在解决最短路问题时,我们通常会采用不同的算法来求解,本文将介绍几种常见的最短路求解方法。
首先,我们来介绍最简单的最短路求解方法——暴力法。
暴力法的思路是枚举所有可能的路径,并找出其中的最短路。
虽然暴力法在理论上是可行的,但在实际应用中,由于其时间复杂度较高,往往不适用于大规模的图。
因此,我们需要寻找更加高效的算法来解决最短路问题。
其次,我们可以考虑使用迪杰斯特拉算法(Dijkstra algorithm)来求解最短路问题。
迪杰斯特拉算法是一种贪心算法,它通过不断地选择距离起点最近的顶点,并更新其邻居顶点的距离,来逐步求解最短路。
迪杰斯特拉算法的时间复杂度为O(V^2),其中V表示顶点的个数。
这使得它在实际应用中具有较高的效率,尤其适用于稠密图的求解。
除了迪杰斯特拉算法外,我们还可以使用弗洛伊德算法(Floydalgorithm)来解决最短路问题。
弗洛伊德算法采用动态规划的思想,通过不断更新图中任意两点之间的最短路径长度,来逐步求解整个图的最短路。
弗洛伊德算法的时间复杂度为O(V^3),因此在大规模图的求解中也具有较高的效率。
除了上述算法外,我们还可以考虑使用A算法、贝尔曼-福特算法等其他算法来解决最短路问题。
这些算法各有特点,适用于不同类型的图和不同的应用场景。
总的来说,最短路问题是一个重要且经典的问题,在实际应用中有着广泛的应用。
在求解最短路问题时,我们可以根据具体的情况选择合适的算法来求解,以提高效率和准确性。
希望本文介绍的几种最短路求解方法能够对读者有所帮助,谢谢阅读!。
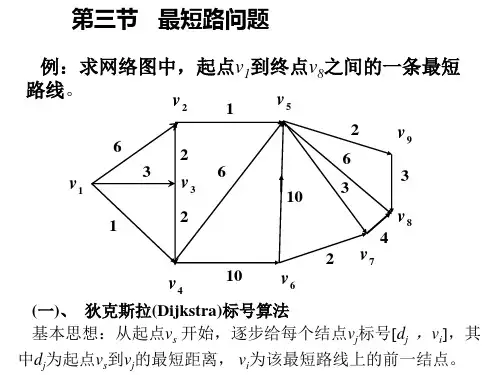

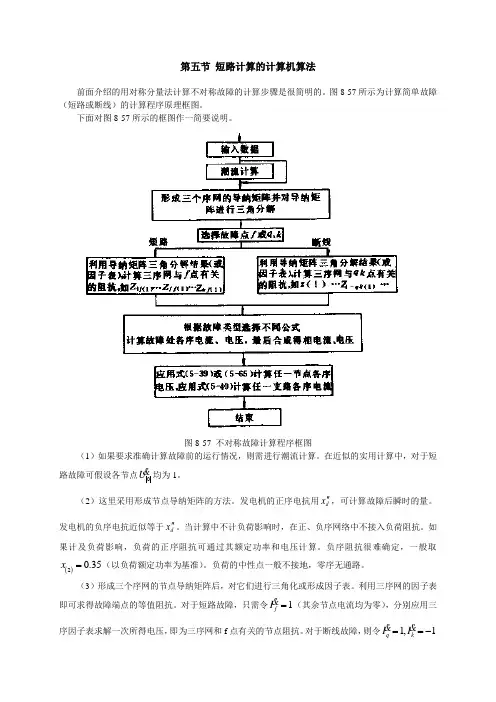
第五节 短路计算的计算机算法前面介绍的用对称分量法计算不对称故障的计算步骤是很简明的。
图8-57所示为计算简单故障(短路或断线)的计算程序原理框图。
下面对图8-57所示的框图作一简要说明。
图8-57 不对称故障计算程序框图(1)如果要求准确计算故障前的运行情况,则需进行潮流计算。
在近似的实用计算中,对于短路故障可假设各节点0U 均为1。
(2)这里采用形成节点导纳矩阵的方法。
发电机的正序电抗用dx '',可计算故障后瞬时的量。
发电机的负序电抗近似等于dx ''。
当计算中不计负荷影响时,在正、负序网络中不接入负荷阻抗。
如果计及负荷影响,负荷的正序阻抗可通过其额定功率和电压计算。
负序阻抗很难确定,一般取()20.35x =(以负荷额定功率为基准)。
负荷的中性点一般不接地,零序无通路。
(3)形成三个序网的节点导纳矩阵后,对它们进行三角化或形成因子表。
利用三序网的因子表即可求得故障端点的等值阻抗。
对于短路故障,只需令1fI = (其余节点电流均为零),分别应用三序因子表求解一次所得电压,即为三序网和f 点有关的节点阻抗。
对于断线故障,则令1,1q kI I ==-(其余节点的电流均为零),分别应用三序因子表求解得各点电压,则故障端口阻抗为:()()()111q k z U U =- ;()()()222q k z U U =- ;()()()000q k z U U =- (8-110) 而其它任一点i 的电压是i 点对故障端口的转移阻抗:()()11i qk i z U -= ;()()22i qk i z U -= ;()()00i qk i z U -= (8-111) 当然,也可以先令1qI = 求解一次,得到与q 有关的节点阻抗,再令1k I = 求解一次,得与k 有关的节点阻抗,则:()()()()()()()11111112qq kk qk i qk iq ik z Z Z Z z Z Z -=+-⎫⎪⎬=-⎪⎭(8-112) 有关节点的负序和零序阻抗,也有类似关系。

运筹学上机实验指导书目录绪论运筹学上机实验软件简介第一章运筹学上机实验指导§1.1 中小型线性规划模型的计算机求解§1.2 大型线性规划模型的编程计算机求解§1.3线性规划的灵敏度分析§1.4运输问题数学模型的计算机求解§1.5目标规划数学模型的计算机求解§1.6整数规划数学模型的计算机求解§1.7 指派问题的计算机求解§1.8最短路问题的计算机求解§1.9最大流问题的计算机求解第二章LINGO软件基础及应用§2.1 原始集(primitive set)和派生集(derived set)与集的定义§2.2 LINGO中的函数与目标函数和约束条件的表示§2.3 LINGO中的数据§2.4 LINDO简介第三章运筹学上机实验及要求实验一.中小型线性规划模型的求解与Lingo软件的初步使用实验二.中小型运输问题数学模型的Lingo软件求解。
实验三.大型线性规划模型的编程求解。
实验四.运输问题数学模型的Lingo编程求解。
实验五.分支定界法上机实验实验六.整数规划、0-1规划和指派问题的计算机求解实验七:最短路问题的计算机求解实验八:最大流问题的计算机求解绪论运筹学是研究资源最优规划和使用的数量化的管理科学,它是广泛利用现有的科学技术和计算机技术,特别是应用数学方法和数学模型,研究和解决生产、经营和经济管理活动中的各种优化决策问题。
运筹学通常是从实际问题出发,根据决策问题的特征,建立适当的数学模型,研究和分析模型的性质和特点,设计解决模型的方法或算法来解决实际问题,是一门应用性很强的科学技术。
运筹学的思想、内容和研究方法广泛应用于工程管理、工商企业管理、物流和供应链管理、交通运输规划与管理等各行各业,也是现代管理科学和经济学等许多学科研究的重要基础。
在解决生产、经营和管理活动中的实际决策问题时,一般都是建立变量多、约束多的大型复杂的运筹学模型,通常都只能通过计算机软件才能求解,因此,学习运筹学的计算机求解和进行上机实验,就是运筹学教学的重要组成部分。

实验一 使用LINGO 求解线性规划问题班级: 姓名: 学号: 评阅成绩: 已知如下线性规划模型:123max 303540z x x x =++1231231231233251823412229,,0x x x x x x x x x x x x ++≤⎧⎪++≤⎪⎨++≤⎪⎪≥⎩ 一、利用集的方法编写上述线性规划模型的LINGO 程序。
在LINGO 软件模型中编写本题的程序如下图1-1所示所示。
图1-1 LINGO 模型窗口截图点击LINGO 菜单下的Solve 选项,LINGO 软件求解所输入的模型,得到LINGO 运行状态窗口如图1-2所示图1-2 LINGO运行状态窗口截图运行结束后,关闭LINGO运行状态窗口,获得LINGO软件的结果报告窗口,如图1-3、1-4所示。
图1-3 LINGO结果报告窗口截图(一)图1-4 LINGO结果报告窗口截图(二)二、根据编写的程序,回答以下问题:1、哪些是原始集?答:var(j), const(i)是原始集2、哪个是派生集?该派生集是稠密集还是稀疏集?该派生集有多少个成员?答:A(i,j)是派生集,属于稠密集合,共有9个成员3、属性值“5”是属于成员(b1,x3)还是(b3,x1)的属性值?答:属于成员(b1,x3)的属性值三、根据程序的运行结果,回答以下问题:1、全局最优值是否已经找到?该值是多少?答:已经找到,最优值为1652、该模型求解一共迭代了多少次?答:共迭代了2次3、在求解结果的界面中,Variable、Value、Reduced Cost、Row、Slack or Surplus 和Dual Price分别表示什么?答:Variable表示运算时各定义变量的取值;Value表示给出最优解中各变量的值;Reduced Cost表示列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时, 目标函数的变化率;Row表示行数;Slack or Surplus 表示给出松驰变量的值;Dual Price表示当对应约束有微小变动时, 目标函数的变化率。
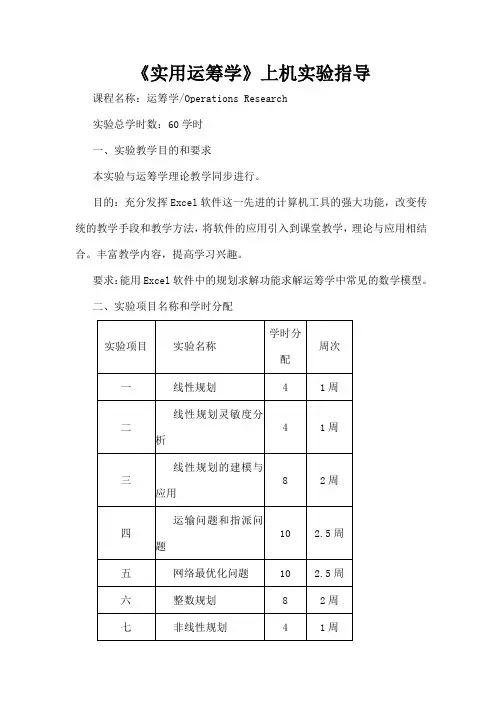
《实用运筹学》上机实验指导课程名称:运筹学/Operations Research实验总学时数:60学时一、实验教学目的和要求本实验与运筹学理论教学同步进行。
目的:充分发挥Excel软件这一先进的计算机工具的强大功能,改变传统的教学手段和教学方法,将软件的应用引入到课堂教学,理论与应用相结合。
丰富教学内容,提高学习兴趣。
要求:能用Excel软件中的规划求解功能求解运筹学中常见的数学模型。
二、实验项目名称和学时分配三、单项实验的内容和要求实验一线性规划(-)实验目的:安装Excel软件“规划求解”加载宏,用Excel软件求解线性规划问题。
(二)内容和要求:安装并启动软件,建立新问题,输入模型,求解模型,结果的简单分析。
(三)实例操作:求解习题1.1。
(1)建立电子表格模型:输入数据、给单元格命名、输入公式等;(2)使用Excel软件中的规划求解功能求解模型;(3)结果分析:如五种家具各生产多少?总利润是多少?哪些工序的时间有剩余,并对结果提出你的看法;(4)在Excel或Word文档中写实验报告,包括线性规划模型、电子表格模型和结果分析等。
案例1 生产计划优化研究某柴油机厂年度产品生产计划的优化研究。
某柴油机厂是我国生产中小功率柴油机的重点骨干企业之一。
主要产品有2105柴油机、x2105柴油机、x4105柴油机、x4110柴油机、x6105柴油机、x6110柴油机,产品市场占有率大,覆盖面广。
柴油机生产过程主要分成三大类:热处理、机加工、总装。
与产品生产有关的主要因素有单位产品的产值、生产能力、原材料供应量与生产需求情况等。
每种产品的单位产值如错误!未找到引用源。
所示。
表 C-1 各种产品的单位产值为简化问题,根据一定时期的产量与所需工时,测算了每件产品所需的热处理、机加工、总装工时,如表 C-2所示。
表 C-2 单位产品所需工时同时,全厂所能提供的总工时如表 C-3所示。
表 C-3 各工序所能提供的总工时产品原材料主要是生铁、焦碳、废钢、钢材四大类资源。

最短路问题的求解方法最短路问题是图论中的一个经典问题,它在现实生活中有着广泛的应用。
在很多实际情况下,我们需要找到两个节点之间的最短路径,以便在最短时间内到达目的地或者以最小的成本进行运输。
因此,求解最短路问题具有重要的意义。
在图论中,最短路问题可以分为单源最短路和多源最短路两种情况。
单源最短路指的是从图中的一个固定节点出发,到达其他所有节点的最短路径;而多源最短路则是求解图中任意两个节点之间的最短路径。
针对这两种情况,我们可以采用不同的算法来求解最短路问题。
其中,最著名的算法包括Dijkstra算法和Floyd-Warshall算法。
Dijkstra算法适用于单源最短路问题,它采用贪心策略,逐步确定从源节点到其他节点的最短路径。
而Floyd-Warshall算法则适用于多源最短路问题,它通过动态规划的方式,计算图中任意两个节点之间的最短路径。
除了这两种经典算法外,还有一些其他方法可以用来求解最短路问题,比如Bellman-Ford算法和SPFA算法。
这些算法各有特点,适用于不同的场景,可以根据具体情况选择合适的算法来解决最短路问题。
在实际应用中,最短路问题常常涉及到大规模的图和复杂的网络结构,因此算法的效率和性能也是非常重要的考量因素。
为了提高算法的求解速度,可以采用一些优化手段,比如使用堆优化的Dijkstra算法、矩阵快速幂优化的Floyd-Warshall算法等。
总之,最短路问题是图论中的一个重要问题,它在实际生活中有着广泛的应用。
通过合理选择算法和优化方法,我们可以高效地求解最短路问题,为实际应用提供有力的支持。
希望本文能够为读者对最短路问题的求解方法有所启发,也希望在未来的实际应用中能够发挥一定的作用。
运筹学最短路问题----------关于旅游路线最短及程序摘要:随着社会的发展,人民的生活水平的提高,旅游逐渐成为一种时尚,越来越多的人喜欢旅游。
而如何才能最经济的旅游也成为人民考虑的一项重要环节,是选择旅游时间最短,旅游花费最少还是旅游路线最短等问题随之出现,如何决策成为一道难题。
然而,如果运用运筹学方法来解决这一系列的问题,那么这些问题就能迎刃而解。
本文以旅游路线最短问题为列,给出问题的解法,确定最短路线,实现优化问题。
关键词:最短路 0-1规划约束条件提出问题:从重庆乘飞机到北京、杭州、桂林、哈尔滨、昆明五个城市做旅游,每个城市去且仅去一次,再回到重庆,问如何安排旅游线路,使总旅程最短。
各城市之间的航线距离如下表:重庆北京杭州桂林哈尔滨昆明重庆0 1640 1500 662 2650 649北京1640 0 1200 1887 1010 2266杭州1500 1200 0 1230 2091 2089桂林662 1887 1230 0 2822 859哈尔滨2650 1010 2091 2822 0 3494昆明649 2266 2089 859 3494 0问题分析:1.这是一个求路线最短的问题,题目给出了两两城市之间的距离,而在最短路线中,这些城市有的两个城市是直接相连接的(即紧接着先后到达的关系),有些城市之间就可能没有这种关系,所以给出的两两城市距离中有些在最后的最短路线距离计算中使用到了,有些则没有用。
这是一个0-1规划的问题,也是一个线性规划的问题。
2.由于每个城市去且仅去一次,最终肯定是形成一个圈的结构,这就导致了这六个城市其中有的两个城市是直接相连的,另外也有两个城市是不连接的。
这就可以考虑设0-1变量,如果两个城市紧接着去旅游的则为1,否则为0。
就如同下图3. 因为每个城市只去一次,所以其中任何一个城市的必有且仅有一条进入路线和一条出去的路线。
解法:为了方便解题,给上面六个城市进行编号,如下表(因为重庆是起点,将其标为1)重庆北京杭州桂林哈尔滨昆明123456假设:设变量x11。
最短路问题的求解方法最短路问题是图论中的经典问题之一,它在实际生活中有着广泛的应用。
在现实生活中,我们经常需要找到两点之间的最短路径,比如在地图导航、网络通信、交通运输等领域。
因此,求解最短路问题具有重要的理论和实际意义。
在图论中,最短路问题可以分为单源最短路和多源最短路两种情况。
单源最短路指的是从图中的一个固定顶点出发,到达图中其他所有顶点的最短路径;而多源最短路则是指图中任意两个顶点之间的最短路径。
在本文中,我们将重点讨论单源最短路问题的求解方法。
求解最短路问题的方法有很多种,其中比较经典的算法包括Dijkstra算法、Bellman-Ford算法和Floyd-Warshall算法。
下面将分别介绍这三种算法的原理和应用。
Dijkstra算法是一种贪心算法,用于解决带权有向图中的单源最短路径问题。
该算法的基本思想是从起始顶点开始,逐步扩展到其他顶点,每次选择距离起始顶点最近的顶点进行扩展,直到扩展到目标顶点为止。
Dijkstra算法的时间复杂度为O(V^2),其中V表示图中顶点的个数。
该算法适用于没有负权边的图,且能够快速求解单源最短路的问题。
Bellman-Ford算法是一种动态规划算法,用于解决带权有向图中的单源最短路径问题,该算法允许图中存在负权边。
Bellman-Ford算法的基本思想是通过对图中的所有边进行|V|-1次松弛操作,其中|V|表示图中顶点的个数。
通过多次松弛操作,可以逐步逼近最短路径的结果。
Bellman-Ford算法的时间复杂度为O(VE),其中V表示图中顶点的个数,E表示图中边的个数。
该算法适用于存在负权边的图,且能够求解单源最短路的问题。
Floyd-Warshall算法是一种动态规划算法,用于解决带权有向图中的多源最短路径问题。
该算法的基本思想是通过对图中的所有顶点进行遍历,逐步更新每对顶点之间的最短路径。
Floyd-Warshall算法的时间复杂度为O(V^3),其中V表示图中顶点的个数。
运筹学实验报告(一)线性规划问题的计算机求解-(1)-CAL-FENGHAI.-(YICAI)-Company One1运筹学实验报告实验课程:运筹学实验日期: 任课教师:王挺第五种方案0 3 0 0第六种方案0 1 1 3第七种方案0 0 2 1设:第i种方案需要的钢管为Xi根(其中i=1,2...6),可得:minz=X1+X2+X3+X4+X5+X6+X7解:model:min= X1+X2+X3+X4+X5+X6+X7;3*X1+2*X2+2*X3+X4>=100;X2+2*X4+3*X5+X6>=150;X3+X6+2*X7>=120;endObjective value: 135.0000Infeasibilities: 0.000000Total solver iterations: 2Variable Value Reduced CostX1 0.000000 0.2500000X2 0.000000 0.1666667X3 50.00000 0.000000X4 0.000000 0.8333333E-01X5 50.00000 0.000000X6 0.000000 0.1666667X7 35.00000 0.0000004人力资源分配问题某昼夜服务的公交线路每天各时间段内所需司机和乘务人员人数如表1所示。
班次时间所需人数班次时间所需人数1 6:00~10:00 60 4 18:00~22:00 502 10:00~14:00 70 5 22:00~2:00 203 14:00~18:00 60 6 2:00~6:00 30设司机和乘务人员分别在各时间段开始时上班,并连续工作8小时,问该公交线路应怎样安排司机和乘务人员,既能满足工作需要,又使配备司机和乘务人员的人数最少?5投资计划问题某地区在今后三年内有四种投资机会,第一种是在3年内每年年初投资,年底可获利润20%,并可将本金收回。