理论塔板简捷计算方法

（2）最少理论板数 ----逐板计算法


若令 ത =

= 1 2 . . . . . .




芬斯克（Fenske）方程
1 2 . . . . . .
xA
N xA

xB D
xB W
N min
x A x B
（2）塔板结构参数
（3）操作参数
4. 填料层高度的计算
如果取一段填料作为一个单元，测得离开这个单元的气液两相组成满足相平衡
关系，则可将这个单元看作一块理论板。而这个单元内包含的填料层高度就称
为等板高度（Height Equivalent of a Theoretical Plate，可以HETP表示 ）。
在实际精馏操作中，由于气液两相的接触时间有限，故离开塔板的气液两相
通常达不到平衡状态。因此，一般用板效率表示实际板与理论板的接近程度。
单板效率也称默弗里（Murphree）板效。

−1
− +1
汽相实际增加程度
= ∗
=
− +1
汽相理论增加程度

---汽相默弗里板效

−1 −
液相实际减少程度
=
=
−1 − ∗
液相理论减少程度
----液相默弗里板效
n
+1

3. 塔板效率和全塔效率
（2）全塔效率E0
理论板数 N
E0

实际板数 N e
其值一定小于1，多数在0.5～0.7之间。
思考：影响塔板效率的因素？
影响塔板效率的因素很多，可概括为以下三大类：

• 绘梯级； NT＝阶梯数－1
不包括 再沸器
NT=5－1=4
（不包括再沸器）
e
b
c
0 xW
xx F
xD 1.0
不同加料热状态下的 q 线
• 图解法求理论板层数时，操作线的更换以某梯级跨过两 操作线交点来判断。
• 将跨过交点的梯级定为进料板。
注意：
每块塔板上平衡 关系及与相邻塔 板上的操作关系 清晰可见。
m
W, xW
泡点进料
xn≤xF
精馏段理论板层数＝n-1
xn＝x’1'
提馏段第一块板 n 板为进料板！
y2'

L' V'
x1'

W V'
xW
操作关系
x2'

y2'
y2'
(1
y2' )
平衡关系
y3'

L' V'
x2'

W V'
xW
操作关系
优点：结果准确， 同时可以得到每块 板上汽液组成。
缺点：当板层数较 多时计算繁琐。
x1

y1
y1
(1
y1)
平衡关系
y1
y1
1
y2 2
x1
x2
F, xF n
ym-2
D, xD
… …
.... ....
y2

R R 1 x1

xD R 1
y2

1
x2 ( 1)x2
x2

y2
y2
(1

VV(q11)F 1 L RD q1F1 V (R1)D(q11)F1
LLq2F2
V'V''(q21)F2
L
R D q1F 1q2F 2
V (R1)D (q11)F 1(q21)F 2
可编辑ppt
12
两股进料的精馏塔最小回流比的确定
可编辑ppt
由ab线斜 率求Rmin1
由ck线斜 率求Rmin2
选择较大 者作为Rmin
18
2）单板效率
单板效率又称默弗里（Murphree）效率，它
是以混合物经过实际板的组成变化与经过理论板 的组成变化之比来表示的。单板效率既可用气相 组成表示，也可用液相组成表示，分别称为气相 单板效率和液相单板效率。
可编辑ppt
19
气相单板效率
EMV
yn yn*
yn1 yn1
液相单板效率
EML
Vs
22.4V 3 600
Tp0 T0 p
可编辑ppt
25
1.5.9 连续精馏装置的热量衡算和节能
1.塔顶冷凝器热量衡算 以单位时间为基准，对冷凝器热量衡算（忽
略热损失）
Q C V IV D (L IL D D IL D ) kJ/h
QC
冷凝器的 热负荷
VI V D
L
I LD
D 冷凝器的
I L D 热量衡算
LV0VW
易挥发组分衡算
L x m V 0 y 0 V y m 1 W x W
可编辑ppt
6
对于塔内恒一摩、尔直流动接蒸汽加热
VV 0 LW
Wxm V0 ym 1WxW
ym 1 W V0 xm W V0 xW
提馏段操 作线方程

理论塔板数公式塔板是一种常用的结构元件，广泛用于建筑、化工、石油、冶金等行业。

它通过平行四棱柱或多头斜安放四棱柱组成，使得结构抗压、抗弯及抗扭性能更加强固。

塔板的抗弯能力决定于板厚及角度大小，其中塔板数是衡量塔板承载能力、抗弯能力的重要指标。

但是，没有一个统一的公式可以计算塔板数，建筑师应根据实际情况来确定塔板数。

实践表明，当塔板的高度处于20米以内时，塔板数可以以物理定律、建筑规范及技术规定来判定，其中包括：物理定律中的垂直力分解定律、相对移动定律、抗拉定律及蒙格雷罗抗弯定律。

下面介绍几种经常用于计算塔板数的公式：其一，板厚法求塔板数，只要将所需塔板厚度乘以柱距即可求得所需塔板数。

但是，塔板厚度一般是固定且经过规范给定，此法适用于所有板厚都相同的计算。

其二、构架跨度法求塔板数，该法以构架跨度作为主要指标，即给定构架跨度则塔板数也就给定，一般构架跨度不超过32米时，即每层塔板的构架跨度不超过32米时，塔板数一般不会大于30块，当构架跨度超过32米时，塔板数需要根据具体情况进行调整。

其三、蒙格雷罗定律求塔板数。

该定律指出，塔板数可以通过将塔板厚度与构架跨度乘积除以塔板跨度来确定。

根据塔板的设计原则，塔板的构架跨度一般控制在34米之间，同时塔板厚度也由设计要求决定，所以当塔板厚度与构架跨度相乘除以塔板跨度所得的塔板数即为理论塔板数。

塔板数的计算是很复杂的问题，建筑师必须根据建筑施工的具体情况来调整塔板数，因此，要想得出合理的塔板数，必须结合实际情况来进行推算计算，对力学原理有较好的理解，以及熟悉设计规范，才能在建筑施工中取得最佳的结果。

以上就是本文关于“理论塔板数公式”的讨论，希望能为建筑师提供参考，让他们更好地理解塔板数的计算方法，从而使建筑施工取得更好的效果。

yW
W xW
➢直线：过点（xW,xW)、截 踞WxW/(L’-W )
xW
a
d
b
xD
R 1
c
xW L W
xW g
xD
精馏塔的操作线
8
二、梯级图解法
提馏段操作线的截距数值很小，因此提馏段操作 线不易准确作出，且这种作图法不能直接反映进料 热状况的影响。
9
q 线方程
精馏段操作线方程 V y = Lx + D xD

xD yq
yq xq
一、全回流和最小回流比
非正常平衡曲线最小回流比的求法
27
2）解析法 对于相对挥发度为常数的情况
Rm

xD yq
yq xq
yp

q q 1
xp

1 q 1
xF
yq
xq 1 ( 1)xq
Rm

1 [ xD
1 xq
(1 xD )]
yB
xB
(
x x
A B
)
D

(
yA yB
)1

1(
xA xB
)1

1(
yA yB
)2

1
2(
xA xB
)2


1 1
2( 2
yyBA3)(3xx
A B
)3

1 1
2 3( 2 3L
yA yB L
)4


W
(
xA xB
)W
(
yA yB
)n1
y q x xF q1 q1
q 线的意义 精馏段操作线与提馏段

整理，得 F (H m,V H m,F ) L L (H m,V H m,L )
L L Hm,V Hm,F
F
Hm,V Hm,L
令q Hm,V Hm,F Hm,V Hm,L
使原料从进料状况变为 饱和蒸汽的摩尔焓变 原料由饱和液体变为饱 和蒸汽的摩尔焓变
化工原理----精馏
L L Hm,V Hm,F q
作业
化工原理----精馏
x x2 x1 xD 1
化工原理----精馏
讨论（图解法）
♫ 优点：简明清晰，便于分析影响因素 ♫ 缺点：计算不够精确
化工原理----精馏
♫（2）梯级的意义
n-1 Xn-1
n xn
n+1
yn-1 yn yn+1
yn yn+1
Xn+1
xn
Xn-1
梯级跨度越大（操作线与平衡线的偏离程度越大），表 示每块理论板的增浓程度越高，则所需理论板数越少。
F
Hm,V Hm,L
L L qF
由上式和进料板 V V (1 q)F
物料衡算，得
q
液化分数
通式
化工原理----精馏
☼2、各种进料热状况下的q值
♫（1）过冷液体进料 q＞1
LV F
♫（2）饱和液体进料 q =1
LV F
L V
过冷液体进料
L V
饱和液体进料
化工原理----精馏
♫（3）汽液混合进料 0＜q＜1
V
♫（4）饱和蒸汽进料 q=0
F
♫（5）过热蒸汽进料 q＜0
L V
过热蒸汽进料
化工原理----精馏
小结
☼ 1、逐板计算法求理论塔板数 ☼ 2、用图解法求理论塔板数

简捷法求理论塔板数的步骤
1.根据物系性质及分离要求，求出Rmin，选择合适的R。
2.求出全回流下所需理论板数Nmin。对于接近理想体系的混合物，可以应用芬斯克方程计算。
感谢观看
依此类推，一直计算到xn≤ xF为止。每利用一次平衡关系式，即表示需要一块理论塔板。
当xn≤xF后，操作线方程改用提馏段操作线方程。其计算步骤和精馏段一样，反复利用操作线方程和气液平 衡关系式，一直计算到xm≤xW为止。
逐板计算法较为准确，不仅应用于双组分精馏计算，而且也可用于多组分精馏计算。但若用手工计算当然相 当繁复，尤其是所计算的塔板数较多时更是如此。
根据对物系的分离要求，用前述方法很容易计算出Rmin和Nmin，困难在于如何按照选定的回流比R，求算所 需的理论塔板数N。通过对R，N，Rmin和Nmin之间关系的广泛研究，得出表示上述4个参数的相互关联图(图 3.33)，此图称为吉利兰图。图中N与Nmin为不包括再沸器的理论板数。
图3.33
应用吉利兰图可以简便地计算出精馏所需的理论板数，这种方法称为简捷法。它的另一个优点是也可以用于 多组分精馏的计算。这种方法的误差较大，一般只能对所需理论板数作大致的估计，因为简便，所以在初步设计 或进行粗略估算时常常使用。
图3.27图解法虽与逐板计算法的依据相同，但较为简便，且直观，便于对过程进行分析比较，但计算的精确 度较差，尤其是对于相对挥发度较小而所需理论塔板数较多的场合更是如此。
简捷算法
吉利兰(Gilliland)关联图
回流比有两个极限：Rmin与全回流，与此对应，回流比为Rmin时所需的理论板数为无穷多，全回流时所需的 理论板数Nmin为最少，实际回流比R在Rmin与无穷大之间．理论板数N在Nmin与无穷多之间。

②提馏段操作关系：
WxW L qF ym1 xm L qF W L qF W
双组分连续精馏塔所需理论板数，可采 用逐板计算法和图解法。
6.7.2 逐板计算法
假设塔顶冷凝器为全凝器，泡点回流，塔 釜为间接蒸汽加热，进料为泡点进料如图6－35 所示。
x1
F, xF
x2 xn xm-1
0.431 0.365<xF 0.301 0.226 0.151 0.089 0.044<xW
精馏塔内理论塔板数为10-1=9块，其中精 馏段4块，第5块为进料板。 （2）图解法计算所需理论板数 在直角坐标系中绘出y-x图（图略）。 根据精馏段操作线方程式（1），找到 a(0.9，0.9)，C(0，0.3)点，联接ac即得到精馏段 操作线。 根据式（2）提馏段操作线，通过 b(0.0667,0.0667)，以1.5为斜率作直线bq，即为 提馏段操作线。
2、方法：
从塔顶到塔底计算。
精馏段：
x D y1 x1 y2
平衡 操作
x2
平衡
xn xq
当xn ＜xq时，q为加料板，因q点为两点操 作线交点，加料板为提馏段一块板，所以精馏 段理论板数为（n-1）块板。
提馏段：（改用提馏段操作线）
xn x
' 1 操作
WxW 144 L' 48 0.0667 ym1 xm xm V' V' 96 96 1.5 xm 0.033
（2 ）
相平衡方程式可写成：
y x ( 1) y 2.47 1.47 y
y
（3 ）
利用操作线方程式（1），式（2）和相平 衡方程式（3），可自上而下逐板计算所需理 论板数。

图3 两条操作线与q线
二、理论塔板数的计算方法
3.图解法
(4)在图3中，过a点（xD、xD）在相平 衡线与精馏段操作线之间画梯级；当跨 过d点（q线与精馏段操作线交点）再在 相平衡线与提馏段操作线之间画梯级； 当跨过c点（xW、xW）则终止。每一个 梯级代表一块理论塔板，得到图解法理 论板数求解图，如图4所示。
算。
提馏段操作线方程：
yn1

L L W
xn

W L W
xw
，得到yn+1 。
相平衡方程：yn1

1
(
xn1 1) xn 1
，得到xn+1 。
二、理论塔板数的计算方法
2.逐板计算法
(2)计算步骤
②提馏段计算
第n+2板：
已知条件：xn+1 ，计算yn+2和xn+2 。
提馏段操作线方程：
二、理论塔板数的计算方法
1.计算条件
由于精馏过程是涉及传热与传质的复杂过程，影响因素很多。因此 需要规定一些计算的条件。 (1)精馏塔对外界是绝热的，没有热损失。 (2)回流液由塔顶全凝器提供，其组成与塔顶产品相同。 (3)恒摩尔气流 精馏段各板V相同，提馏段各板V′相同。 (4)恒摩尔溢流 精馏段各板L相同，提馏段各板L′相同。
C. 气液相平衡方程
D. 以上都包括
2. 判断题
(1) 在图解法求解理论塔板数中，步骤是过a点（xD、xD）在相平衡线与 精馏段操作线之间画梯级，在d点（精馏段操作线与q线的交点）之后仍在
相平衡线与精馏段操作线之间作若干个梯级。之后，才转为在相平衡线与
提馏段操作线之间作梯级，直到跨过c点终止。（ ）

共需9块理论塔板，在第5块塔板进料。
2.捷算法求理论塔板数
由芬斯克公式：
N min
lg
1
x
D
x
D
1 xW xW
lg lg 0.9 1 0.0667
1 0.1 0.0667
lg 2.47 5.35
X R Rm 1.875 1.25 0.217
R 1
2.875
由吉利兰关联式：Y 0.75(1 X ) 0.567 0.439
y6 1.522 0.359 0.0359 0.51
y5 0.58 x5 0.359 xF
x6
y6 2.47 1.47 y6
0.51
0.296
2.47 1.47 0.51
y7 0.415 x7 0.186
y8 0.247 x8 0.117
y9 0.147 x9 0.0629 xW 0.0667
xm
W RD F
W
xW
y m1
1.875 40 100 1.875 40 100 60
xm
60 0.0667 (1.875 1)40
1.522xm
0.0369
相平衡方程为：x
y
y
( 1) y 2.47 1.47 y
1.利用逐板法求理论塔板数：
y1 xD＝0.9(泡点回流）
x1
y1 2.47 1.47 y1
解： D＝FxF xD 0.9 100 0.4 / 0.9 40kmol / h
W F D 100 40 60kmol / h
xW
FxF DxD W
100 0.4 40 0.9 60
0.0667
q线与平衡线的交点为：xq xF 0.4

④确定加料位置。可把加料组成
看成釜液组成求出理论板数，即 为精馏段所需的理论板数，从而 确定加料位置。
R Rmin R1
注意：上述计算中的N 和Nmin均不包括再沸器。
GLL
【例8-7】用连续精馏塔分离苯-甲苯混合物。已知xF=0.501(摩尔分数，下 同)，xD=0.98，xW=0.03，R=4，精馏段和全塔的平均相对挥发度分别为 2.52和2.50。试用简捷法计算泡点进料时的理论板数和加料板的位置。
------对角线
全回流操作只适用于精馏塔的开工、 调试及实验研究。
全回流时操作线与平衡线的距离最 远，达到相同的分离程度所需的理 论板数最少，以 Nmin 表示。
xW xD
GLL
最小理论板数 全回流时的理论板数 Nmin 可用逐板计算法或图解法求得。 对理想溶液，可由芬斯克（Fenske）方程直接计算得。 芬斯克 (Fenske) 方程
逐板计算法 根据苯的回收率计算塔顶产品流量
D
Fx F
xD

0.9 80 0.4 32kmol / h 0.9
则
W F D 80 32 48kmol / h
xW
Fx F Dx D 80 0.4 32 0.9 0.0667 W 48
已知R=2，所以精馏段操作线方程为
理论板数的计算
对符合恒摩尔流假设的双组分精馏过程，以操作线方程和相 平衡关系为依据，用逐板计算法和图解法确定N 。 逐板计算法
yn K n xn
y1 y1 y2
yn1 ym 1
R xD xn R1 R1 WxW L' xm V' V'
F, xF
1 2

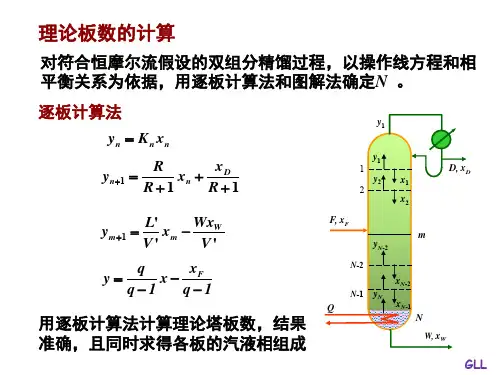
6.4.6 理论塔板简捷计算方法目标：了解简捷计算法及使用条件（1）最少理论板数a.全回流操作一精馏塔在操作过程中，将塔顶蒸气全部冷凝，其凝液全部返回塔顶作为回流，称此操作为全回流，回流比R为无穷大（R=∞）。

此时通常不进料，塔顶、塔底不采出。

故精馏塔内气、液两相流量相等，L=V，两操作线效率均为1，并与对角线重合，如图6.4.15所示。

塔内无精馏段和提馏段之分，其操作线方程可表示为：（6.4.8）图 6.4.15全回流操作的最小理论塔板由于全回流操作时，使每块理论板分离能力达到最大，完成相同的分离要求，所需理论板数最少，并称其为最小理论板数。

最少理论板数由以下芬斯克方程求得：对双组分精馏，A，B两组分相对挥发度表示为j=1，2… N (6.4.9)由塔内操作线方程式（6.4.8）可得或（6.4.10）将各级相平衡关系相乘：运用式（6.4.10）化简，在各板上的相对挥发度近似取为常数，则通过简化和整理获得Fenske方程：该方程也可用于多组分精馏，其区别是以轻、重关键组分的分离代替双组分的精馏。

芬斯克方程推导6.4.6 理论塔板简捷计算方法（续）（2）简捷计算法将许多不同精馏塔的回流比、最小回流比、理论板数及最小理论板数即R、Rmin、N、Nmin四个参数进行定量的关联。

常见的这种关联如图所示，称为吉利兰图（Gillilad）图，如图6.4.16所示。

图 6.4.16 吉利兰图·计算·由图6.4.16或式（6.4.11）求解Y值，代入下式。

·解得理论板数N及Nmin均含再沸器理论板。

采用简捷法也可估算精馏塔精馏段及提馏段理论塔板数或进料位置。

如果计算精馏段理论塔板数，则求精馏段最少理论板数，由进料组成代替，为精馏段平均相对挥发度，按以上步骤求得精馏段理论板数。

同理，求得提馏段理论板数。

例6.4.26.4.7 几种蒸馏操作方式的讨论目标：介绍几种不同操作的精馏过程在精馏过程中，常常有加热、进料方式不同，根据要求，其采出方式也有所区别，对此，分别讨论如下：（1）直接蒸气加热一般精馏是间接加热，主要是为避免对物料污染。

图解法求理论板，进料位置由 两操作线交点确定，在跨越交点 的梯级上。
1
2
a
3
f4
5d
6
e
7
b8 c
xW
xF
xD
理论塔板数
实际塔板数的确定
全塔效率 ：在指定的分离条件下，所需的理论塔板数NT（不包括塔釜）与 实际塔板数N之比，用符号ET表示。即
ET
NT N
则实际塔板数：
N NT ET
L
泡罩塔塔板效率关系曲线
（2）画出三条操作线
（3）画直角梯级：从塔顶a点 开始，跨越d点，到达c点结束
每一个梯级顶点代表一层 理论板，过d点为进料板， 末级为再沸器
1
2
a
3
f4
5d
6
e
7
b8 c
xW
xF
xD
理论塔板数
图解法
最适宜的进料位置 一般应在塔内液相或气相组成
与进料组成相同或相近的塔板上 ，分离效果好或一定的分离要求 所需理论板较少。
yn1
R R
1
xn
1 R
1
xD
ym1
L qF L qF W
xm
L
W qF
W
理论塔板数
逐板计算法
精馏段 从塔顶开始 ：塔顶采用全凝器，泡点回流
y1 xD (已知）
y1
1
x1 ( 1)x1
y1 x1(平衡关系)
x1
y1
1
y1
x1 y2（操作关系）
y2
R R 1
x1
xD R 1
理论塔板数
逐板计算法
精馏段
x
y
1
y

一
递 过程 而言 ， 两相 流率 沿塔 高无 明显 变化 ， 且传 质
过 程为 等温 操作 ， 传质 系数 也视 为 常量 。因此 ， 在
这 三种 操作 中 ， 描述 低 含 量 物 质 传 递过 程 的操 作
线 均 为一 直 线 ， 斜 率 为 两相 流 率之 比 。表 １分 别 给出 了这 三 种 操 作 所 对 应 的 操 作 线 和 平 衡 线 方
无论何种传质设备理论塔板数的计算是传质过程设计和操作中的一项重要内容求理论塔板数的方法常用方法是图解法即将相平衡线方程以及组分的操作线方程绘制成图线然后在操作线与平衡线之间按照组分的初值及终值逐级划出阶梯线所得的梯级数即为理逐板计算法与此法类似取吸收塔质作物料衡算直到气相组成者简介宗原1982传质分离过程理论塔板数的简捷计算83别当逐步离开塔段即在曲线末端时实际误差较大
、
捷算 法 推导 过程
气体 吸 收／ 解吸 、 液体精馏及液液萃取 （ 稀 释
程， 以及 各参 数 的物 理含 义 。
表 １ 气 体 吸收／ 解 吸、 精馏 及 萃取 的操 作线及 平衡 线方 程
传 质操 作 操 作线 方程
ｙ 一
平衡 线方程
气 体 吸收
Ｌ，
Ｌ ｚ ～ 进 Ｊ十 出
［ 摘要］ 本文 在 图解 法的基 础上 ， 通过 分析 理论 塔板 与 操作 线 、 平 衡线 之 问 的关 系 ， 建 立 了适 用 于 气 体 吸 收、 液 体精 馏及 液 液莘取 过 程 的传 质 单元 数 与理论板 数 间 的对 应 关 系， 并 利用 工 业 低含 量物 质传 质过 程 ， 对此关系 式进 行验 证 。与 实际 比较 ， 结 果基 本 一致 ， 且 计算 过程 简单 、 快捷 ， 可 帮助 学生加 深 对传质 过程 的认 识 。 ［ 关键词］ 气 体 吸 收 ；传 质 单 元 数 ； 理 论 板

αm为全部理论塔板上平均相对挥发度，可取为塔顶第一块板上及塔釜中相平 衡体系相对挥发度的几何平均，即
α m = α Dα w
③利用吉利兰图，算出选定回流比R对应的全塔理论板数N（不含再 沸器）。
④确定加料板位置 用Fenske方程估算全回流时精馏段所需的最少理论板数N’min， 再利用前述Rmin，查吉利兰图，算出选定回流比R时精馏段所需总 理论板数N’。加料板为N’+1。 应用Fenske方程估算精馏段塔板数的方法：
(曲线右端点)
0.01
R − Rmin R +1
1.0
R = Rmin
lim
N → +∞
(曲线左端点)
R − Rmin =0 R → Rmin R +1 N − N min 1 − N min N lim = lim =1 R → Rmin N → +∞ 1 + 2 N N +2
（吉利兰图本质是反映N~R之间 的函数关系）
L' W y 'm +1 = x'm − xw V' V'
√√ √ √
L' L + qF L + qF RD + qF = = = V ' V + ( q − 1) F L + D + ( q − 1) F ( R + 1) D + ( q − 1) F √
√ √ √
两种情况下提馏段操作线的斜率相同。
y s +1
D1 x D1 + D2 x D 2 RD1 − D2 xs + = ( R + 1) D1 ( R + 1) D1

理论塔板数的计算一、逐板计算法精馏段操作线方程： 提馏段操作线方程： 相平衡方程： 或第一板：第二板：…… 第m 板：第m+1板： (1)11+++=+R x x R R y D n n w m m x R f x R R f y 1111+--++=+nn n x x y )1(1-+=ααnn n y y x )1(--=ααD, V, L, xD F,xx y m m-逐板计算示意图 111)1(y y x --=ααDx y =11112+++=R x x R R y D 222)1(y y x --=αα111+++=-R x x R R y D m m F m m m x y y x ≤--=)1(αα第m 板为进料111)1(+++--=m m m y y x ααw m m x R f x R R f y 1111+--++=+第N 板：在计算过程中, 每使用一次平衡关系, 表示需要一层理论板. 由于一般再沸器相当于一层理论板.结果: 塔内共有理论板N 块, 第N 板为再沸器, 其中精馏段m-1块, 提馏段N-m+1块 (包括再沸器), 第m 板为进料板。

二、图解法图解法求理论板层数的基本原理与逐板计算法的完全相同,只不过是用平衡曲线和操作线分别代替平衡方程和操作线方程,用简便的图解法代替繁杂的计算而已。

1、操作线的作法首先根据相平衡数据, 在直角坐标上绘出待分离混合物的x-y 平衡曲线, 并作出对角线.W NN N x y y x ≤--=)1(ααw N N x R f x R R f y 1111+--++=-在x=xD 处作铅垂线, 与对角线交于点a, 再由精馏段操作线的截距xD /(R+1) 值, 在y 轴上定出点b, 联ab. ab为精馏段操作线.在x=xF 处作铅垂线, 与精馏段操作线ab交于点d.在x=xW 处作铅垂线, 与对角线交于点c, 联cd. cd为提留段操作线.2、求N 的步骤自对角线上a点始, 在平衡线与精馏段操作线间绘出水平线及铅垂线组成的梯级.当梯级跨过两操作线交点d 时, 则改在平衡线与提馏操作线间作梯级, 直至某梯级的垂直线达到或小于xw为止.每一个梯级代表一层理论板. 梯级总数即为所需理论板数.3、梯级含义：如第一梯级:由a点作水平线与平衡线交于点1(y1, x1), 相当于用平衡关系由y1求得x1；再自点1作垂线与精馏段操作线相交, 交点坐标为(y2, x1), 即相当于用操作线关系由x1求得y2。

精馏过程的物料衡算和塔板数的计算一、理论塔板连续精馏计算的主要对象是精馏塔的理论塔板数。

所谓的理论塔板是指气液在塔板上充分接触，有足够长的时间进行传热传质，当气体离开塔板上升时与离开塔板下降的液体已达平衡，这样的塔板称为理论塔板。

实际上，由于塔板上气液接触的时间及面积均有限，因而任何形式的塔板上气液两相都难以达到平衡状态，也就是说理论塔板是不存在的，它仅是一种理想的板，是用来衡量实际分离效率的依据和标准。

通常在设计中先求出按生产要求所需的理论塔板数N T然后用塔板效率η予以校正，即可求得精馏设备中的实际塔板数N P二、计算的前提由于精馏过程是涉及传热、传质的复杂过程，影响因素众多。

为处理问题的方便作如下假设，这些就是计算的前提条件。

（1）塔身对外界是绝热的，即没有热损失。

（2）回流液由塔顶全凝器供给，其组成与塔顶产品相同。

（3）塔内上升蒸气由再沸器加热馏残液使之部分气化送入塔内而得到。

（4）恒摩尔气化在精馏操作时，在精馏段内，每层塔板上升的蒸气的摩尔流量都是相等的，提馏段内也是如此，即：精馏段：V1 = V2 = …………＝Ｖn= Vmol/s(下标为塔板序号，下同）提馏段：Ｖ′n+1 =V′n+2 =…………＝V′m= V′mol/s但Ｖn不一定与Ｖ′m相等，这取决于进料状态。

（５）恒摩尔溢流（或称为恒摩尔冷凝）精馏操作时，在精馏段内每层塔板下降的液体的摩尔流量都是相等的，提馏段也是如此，即：Ｌ1 = L2=…………= L n = L mol/sL′n+1= L′n+2=………… = L′m= L′ mol/s但Ｌ不一定与Ｌ′相等，这也取决于进料的状态。

（６）塔内各塔板均为理论塔板。

三、物料衡算和操作线方程１、全塔物料衡算图4-10 全塔物料衡算示意图如图４－１０所示，设入塔进料流量为Ｆ，轻组分含量为x F,塔顶产量流量为Ｄ，轻组分含量为x D,塔底产品流量为Ｗ，轻组分含量为x w，流量单位均为mol/s，含量均为摩尔分率。