spss操作独立样本T检验模板

一、被调查学生对“云窗的打分值”总体平均值的推断：1、以71个被调查学生为样本做T 检验由表a 可知，71个观测的平均值为71.21，标准差为15，120，均值标准误为1.794。

表b 中，第二列是t 统计量的观测值为0.675，第三列是自由度n-1=70，第四列是t 统计量观测值的双尾概率p 值，第五列是样本均值与检验值的差（1.211），即t 统计量的分子部分，他除以表a 的均值标准误（1.794）后得到t 统计量的观测值0.675，第六列和第七列是总体均值与检验值差的95%的置信区间，为（67.63，74.79）。

对于研究的问题应采用双尾检验，因此比较2α和2p，即比较α和p 。

由于p 大于α（0.05），因此不能拒绝零假设，认为被调查学生对“云窗的打分值”总体平均值没有显著差异。

有95%的把握认为总体均值在 67.63~74.79 分之间。

70分包含在置信区间内，也证实了上述推断。

2、被调查学生对“云窗的打分值”的重抽样自举表cBootstrap 指定采样方法简单箱图样本数1000置信区间度95.0%置信区间类型百分位由表c可知，自举过程执行1000次，随机数种子指定为默认值2000000，采样方法为简单箱图。

中均值的重抽样自举均值与实际样本均值的差为-0.12，1000个均值的标准差为1.82，由此得到的均值95%的置信区间为（67.18，74.46）表e中没有给出双尾检验的概率p值，但是从检验的结果可知有95%的把握认为总体均值在67.184~74.463之间。

70包含在置信区间内。

用更大的样本量再一次说明了被调查学生对“云窗的打分值”总体平均值没有显著差异。

例题
比较两批电子器材的电阻，随机抽取的样本测量电阻如题表2所示，试比较两批电子器材的电阻是否相同？（提示：需考虑方差齐性问题）
分析步骤：
单击工具栏“分析”——>单击“比较均值”——>单击“单因素ANOVA检验”——>因变量列表置为电阻——>因子置为类别——>选项——>选中方差齐性检验
图1 单因素ANOVA检验
图2 统计
单击工具栏“分析”——>单击“比较均值”——>单击“独立样本T检验”——>检验变量置为电阻——>单击定义组——>填入A批、B批——>单击“确定”
图3 独立样本T检验结果展示：
表4：独立样本检验
结果分析：
假设A,B两批电阻相互独立且均服从正态分布。

H0：u1-u2＝0，两批电阻器材的电阻相同
H1：u1-u2≠0，两批电阻器材的电阻不相同
1、查看表4莱文方差等同性检验（levene），假定等方差（显著性为0.435>0.05，代表方差是齐性的），我们看第一行数据。

t检验结果显示，t=1.648，v=12，P=0.125>0.05，按照检验水准，接受H0，拒绝H1，故两批电阻器材的电阻相同。

2、查看表4莱文方差等同性检验（levene），不假定等方差，我们看第二行数据。

t’检验结果显示，t=1.648，v=10.671，P=0.129>0.05，按照检验水准，接受H0，拒绝H1，故两批电阻器材的电阻相同。

独立样本T检验SPSS操作
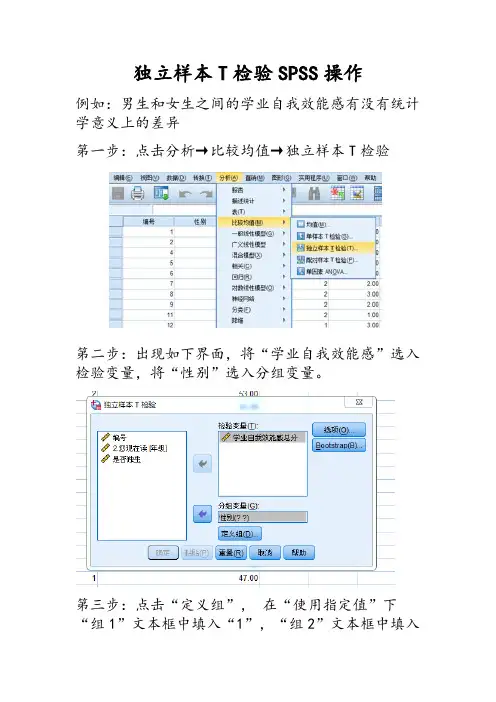
例如：男生和女生之间的学业自我效能感有没有统计学意义上的差异
第一步：点击分析→比较均值→独立样本T检验
第二步：出现如下界面，将“学业自我效能感”选入检验变量，将“性别”选入分组变量。

第三步：点击“定义组”，在“使用指定值”下“组1”文本框中填入“1”，“组2”文本框中填入
“2”（因为数据中“1”代表男生，“2”代表女生），然后点击“继续”。

第四步：点击“确定”，出现得到T检验的结果。

第五步：分析结果。

第一张表的名字叫组统计量，实际上这个性别就是男性组和女性组，即按照不同的组别进行分组。

统计出男性组和女性组每一组的均值和标准差。

一列数据是可以选择用均值和标准差来表示的，均值表示的是这一组的学业自我效能感分数的一个均衡状态，标准差反映的就是同学们得分与这个均衡状态的这个偏离程度。

男性和女性在均值上的差异是否具有统计学意义，我们还需要继续考察独立样本T检验的表。

假设方差相等，看F和F对应的显著性水平，要看显著性水平是不是小于0.05，判断方差是否齐性。

若这个数小于0.05，说明假设方差相等的可能性小
于0.05，小概率事件发生，拒绝原假设，即假设方
差不相等，看第二行的数据t和t对应的显著性水平。

如果方差齐性，也就是sig值大于0.05，就看第一
行的数据。

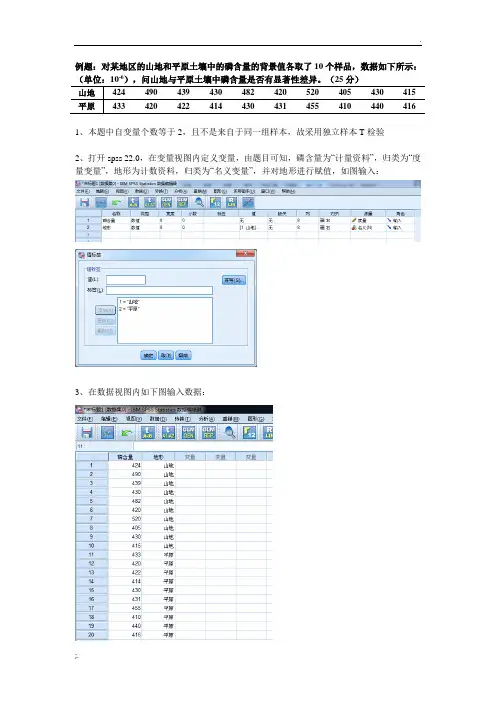
例题：对某地区的山地和平原土壤中的磷含量的背景值各取了10个样品，数据如下所示：-6山地424 490 439 430 482 420 520 405 430 415 平原433 420 422 414 430 431 455 410 440 4161、本题中自变量个数等于2，且不是来自于同一组样本，故采用独立样本T检验2、打开spss 22.0，在变量视图内定义变量，由题目可知，磷含量为“计量资料”，归类为“度量变量”，地形为计数资料，归类为“名义变量”，并对地形进行赋值，如图输入：3、在数据视图内如下图输入数据：4、独立样本T检验进行的假设：(1)数据必须为连续性数据；(2)方差齐性(可偏不齐，即σ12/σ22<3)；(3)每组数据均服从正态分布5、进行验证：(1)由题目可以看出，数据为连续型数据，满足；(2)此检验可于结果中查看；(3)首先，新建spss视图，重新输入变量进行探索队列，如下图所示：将“山地”“平原”选入因变量列表，并于“绘图(T)”中勾选“带检验的正态图”，操作步骤如下图所示：根据正态性检验表的“K-S检验”结果，由于样本内数据数量<30，故看Shapiro-Wilk结果，由于两者的sig均大于0.05，故满足正态分布正态性检验Kolmogorov-Smirnov(K)a Shapiro-Wilk统计df 显著性统计df 显著性山地.268 10 .041 .856 10 .069平原.146 10 .200*.945 10 .608*. 这是真正显著性的下限。

a. Lilliefors 显著性校正6、进行独立样本T检验：(1)依次点击“分析”-“比较平均值”-“独立样本T检验”，调出独立样本T检验对话框：(2)将“磷含量”选入检验变量(T)，将“地形”选入分组变量，然后定义组，于主页面中点击“确定”，输出结果：组统计地形数字平均值(E) 标准偏差标准误差平均值磷含量山地10 445.50 38.106 12.050 平原10 427.10 13.609 4.304独立样本检验列文方差相等性检验平均值相等性的t 检验F 显著性t自由度显著性（双尾）平均差标准误差差值差值的95%置信区间下限上限磷含量已假设方差齐性9.559 .006 1.438 18 .168 18.400 12.796 -8.482 45.282未假设方差齐性1.438 11.259 .178 18.400 12.796 -9.684 46.484根据独立样本检验表的方差方程的Levene检验，F统计量的sig值0.006<0.05，否认方差相等的假设，认为方差不齐性，故参考第二行的t检验结果；第二行t检验的双侧sig=0.178>0.05，即可认为在0.05的显著性水平上，山地与平原土壤中磷含量是否没有有显著性差异。

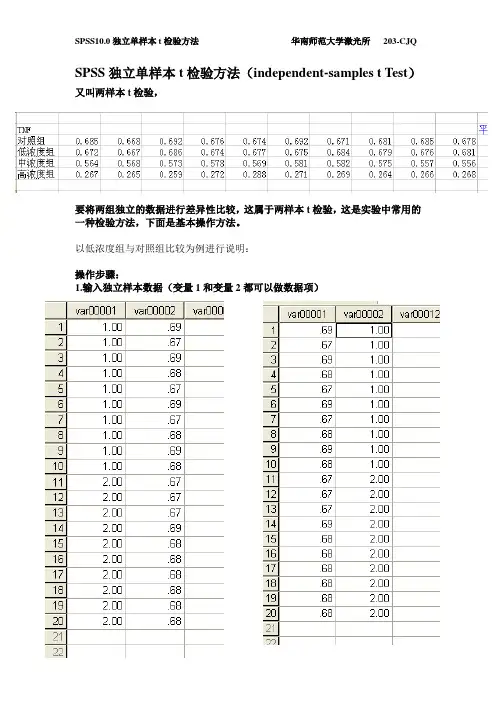
SPSS独立单样本t检验方法（independent-samples t Test）又叫两样本t检验，
要将两组独立的数据进行差异性比较，这属于两样本t检验，这是实验中常用的一种检验方法，下面是基本操作方法。

以低浓度组与对照组比较为例进行说明：
操作步骤：
1.输入独立样本数据（变量1和变量2都可以做数据项）
2.选用程序
从菜单选择Analysize——Compare Mean——Independent-samples t Test,打开对话框，分别将数据变量组和组别变量组对应的var转入右边对应的空白框中，数据变量组转到Test Variable(s),组别变量组转到Grouping Variable
转入后，在定义组别，
点击Difine Groups…按钮，出现如下对话框，然后输入对应的组别号，在这个例子中，group1是用1来表示的，group2使用2表示的。

因此，分别输入1和2，再点击Continue按钮。

点击continue按钮后出现如下对话框，再点击OK，这样独立样本T检验程序定义完成。

3.结果分析
在第二步最后点击OK后，软件的分析结果就会出现，如下图，红框里就是要的数据。

经Levene’s方差齐性检验，F=4.655，而P=0.045<0.5,认为两组总体方差是齐的，就看两样本t检验的第一横列的值（也就是跟F同列的值）：t=1.353，P=0.193，按P=0.05水准，P>0.05,则两样本物显著性差异，P<0.05,有显著性差异，P<0.01时，两样本有极大差异。

如果F的P>0.5，则认为两样本总体方差不齐，则看第二横列的值，t检验的P值分析同上。

两独立样本T检验-SPSS操作详解为了解某一新药降血压的效果，将28名高血压患者随机分为实验组和对照组，实验组采用新药，对照组采用常规药，测得治疗前后的血压变化，问新药是否优于常规药？编号 1 2 3 4 5 6 7 8 9 10 11 新药前102 100 92 98 118 100 100 92 126 117 109 后90 90 85 90 114 95 86 88 102 92 98编号 1 2 3 4 5 6 7 8 9 10 11 常规前98 110 109 94 110 92 95 90 108 90 110 药后100 103 105 98 109 95 94 88 104 85 110变量1设置：name-group , decimals-0 , label-分组, value-(1=新药，2=常规药) 变量2设置：name-value , decimals-0 , label-血压下降值2 输入数据---血压差=用药前血压-用药后血压3 单击菜单栏analyze/compare means/independent-samples t test4 将血压下降值调入test variables下矩形框5 将分组（group）调入grouping variable 下矩形框6单击define groups…定义分组group1为1 定义group2为2 单击continue7 options选项默认8 bootstrap选项默认9 单击OK 输出结果10 结果界面11 结果解释表1表示两独立样本t检验基本统计量-group statistics表2表示两独立样本t检验结果，方差方程的levene检验（Levene’s Test forEquality of Variances 方差齐性检验）F=3.115，P=0.93，认为两样本来自的总体方差齐。

T检验中t=3.18，P=0.005。

在统计学中，我们往往从样本的特性推知随机变量总体的特性。

但由于总体中个体之间存在差异，样本的统计量和总体的参数之间往往会有误差。

因此，均值不相等的样本未必来自不同分布的总体，而均值相等的样本未必来自有相同分布的总体。

也就是说，如何从样本均值的差异推知总体的差异，这就是均值比较的内容。

SPSS提供了均值比较过程，在主菜单栏单击“Analyze”菜单下的“Compare Means”项，该项下有5个过程，如图4-1。

平均数比较Means过程用于统计分组变量的的基本统计量。

这些基本统计量包括：均值（Mean）、标准差(Standard Deviation)、观察量数目(Number of Cases)、方差(Variance)。

Means过程还可以列出方差表和线性检验结果。

[例子]调查了棉铃虫百株卵量在暴雨前后的数量变化，统计暴雨前和暴雨后的统计量，其数据如下：暴雨前 110 115 133 133 128 108 110 110 140 104 160 120 120暴雨后 90 116 101 131 110 88 92 104 126 86 114 88 112该数据保存在“DATA4-1.SAV”文件中。

1）准备分析数据在数据编辑窗口输入分析的数据，如图4-2所示。

或者打开需要分析的数据文件“DATA4-1.SAV”。

图4-2 数据窗口2）启动分析过程在SPSS主菜单中依次选择“Analyze→Compare Means→Means”。

出现对话框如图4-3。

图4-3 Means设置窗口3）设置分析变量从左边的变量列表中选中“百株卵量”变量后，点击变量选择右拉按钮，该变量就进入到因子变量列表“Dependent List:”框里，用户可以从左边变量列表里选择一个或多个变量进行统计。

从左边的变量列表中选中“调查时候”变量，点击“Independent List”框左边的右拉按钮，该变量就进入分组变量“IndependentList”框里，用户可以从左边变量列表里选择一个或多个分组变量。

独立样本T检验下面我们要用SPSS来做成组设计两样本均数比较的t检验，选择Analyze==>Compare Means==>Independent-Samples T test，系统弹出两样本t检验对话框如下：将变量X选入test框内，变量group选入grouping框内，注意这时下面的Define Groups按钮变黑，表示该按钮可用，单击它，系统弹出比较组定义对话框如右图所示：该对话框用于定义是哪两组相比，在两个group框内分别输入1和2，表明是变量group取值为1和2的两组相比。

然后单击Continue按钮，再单击OK按钮，系统经过计算后会弹出结果浏览窗口，首先给出的是两组的基本情况描述，如样本量、均数等（糟糕，刚才的半天工夫白费了），然后是t检验的结果如下：Levene's TestforEqualityofVariancest-test for Equality of MeansFSig.tdfSig.(2-tailed)MeanDifferenceStd.ErrorDifference95%ConfidenceInterval ofthe Difference体方差是否齐，这里的戒严结果为F = ，p = ，可见在本例中方差是齐的；第二部分则分别给出两组所在总体方差齐和方差不齐时的t检验结果，由于前面的方差齐性检验结果为方差齐，第二部分就应选用方差齐时的t检验结果，即上面一行列出的t= ，ν=22，p=。

从而最终的统计结论为按α=水准，拒绝H0，认为克山病患者与健康人的血磷值不同，从样本均数来看，可认为克山病患者的血磷值较高。

SPSS统计分析示例
例二：
将20名某病患者随机分为两组，分别用甲乙两药治疗，测得治疗前后的血沉（mm/小时）如下表：
试分甲乙两药是否有疗效？两药疗效是否有差异？并用图或表对数据和结果进行描述。

1．对两种药物治疗效果比较的统计分析
（以下结果均使用SPSS统计软件获得）
（1）对甲药疗效做配对t检验：
治疗前后血沉值的差值的配对检验SPSS结果显示：t=5.237(df=9)，单侧检验P=0.001x2<0.01，结论甲药疗效极显著。

（2）对乙药疗效做配对t检验：
治疗前后血沉值的差值的配对检验SPSS结果显示：t=5.303(df=9)，单侧检验P<<0.01，结论乙药疗效极显著。

（3）对甲药、乙药的疗效做独立双样本的t-检验
由SPSS输出表可知：甲药、乙药给药后血沉差值样本数据满足方差齐性要求，t=-1.602(df=18)，双侧检验P=0.127>0.05，则两种药的疗效无显著差异。

汇总表
服药前服药后差值t
甲药mm/h (M±SD) 8.7±2.4 5.5±3.1 3.2±1.9 5.237**
乙药mm/h (M±SD) 9.6±1.8 4.6±2.0 5.0±3.0 5.303**
甲药与乙药比较 1.602 **:P<0.01。

独立样本T检验
可见该结果分为两大部分：第一部分为Levene's方差齐性检验，用丁判断两总体方差是否齐，这里的戒严结果为 F = 0.032 , p = 0.860 ,可见在本例中方差是齐的；第二部分则分别给出两组所在总体方差齐和方差不齐时的t检验结果，由丁前面的方差齐性检验结果
为方差齐，第二部分就应选用方差齐时的t检验结果，即上面一行列出的t= 2.524 , v =22,
p=0.019。

从而最终的统计结论为按a =0.05水准，拒绝H0,认为克山病患者与健康人的血磷值不同，从样本均数来看，可认为克山病患者的血磷值较高。

spss操作独立样本T检验模板.doc一、独立样本T检验的基本概念独立样本T检验是指用于比较两个独立样本平均数是否有显著差异的统计方法。

其中，独立样本是指两组样本各自独立，互不干扰，不相关的情况。

例如，对于两组人员，第一组接受了药物治疗，第二组未接受药物治疗，比较两组人员的体重是否有差异。

在这个例子中，两组人员是独立的。

二、SPSS独立样本T检验的操作步骤（一）数据收集导入在进行独立样本T检验之前，需要先确定要对比的两组数据，并将数据收集起来。

将数据按不相同的组别（如服用药物和未服用药物）分别输入到SPSS中，分别为组别A和组别B。

（二）前期处理在开始分析之前，需要先做一些数据预处理工作，包括数据清洗、离群值检查和变量分布及可视化统计分析等。

（三）执行独立样本T检验1. 打开SPSS，依次选择"分析"-"比较均值"-"独立样本T检验"。

2. 将需要检验的变量（如体重）拖到"测试变量列表中"栏位中。

3. 选择独立样本的两个组别（如A组和B组），将其拖到独立样本列表（"样本1"和"样本2"）中。

4. 选择置信度（Confidence Interval）和显著性水平（Significance Level）。

5. 点击"OK"，等待SPSS自动为我们生成结果。

（四）检验结果解释SPSS生成的独立样本T检验结果包括了三个表格，分别是"平均数和标准误"、"独立样本T检验"和"效应大小"。

1. "平均数和标准误"表格：这个表格显示了每一组别数据的均值（Mean）和标准误（Standard Error），同时还包括组别的样本量（N）和方差（Variance）等信息。

2. "独立样本T检验"表格：这个表格包含了检验结果的详细信息，包括了统计学指标（如t值和P值）、置信区间（Confidence Interval）和自由度（Degrees of Freedom）等信息。

一、问题与数据某班级老师拟比较该班级本次考试中，男生和女生的考试成绩是否有差异，该班级男生和女生各有20名同学，变量名记录为gender，分别赋值为1和2，考试成绩变量名记录为score，部分数据如图1。

图1 部分数据二、对问题分析研究者拟分析两组数据均值是否有差异，即判断男生和女生的成绩是否有差异。

针对这种情况，我们可以使用独立样本t检验，但需要先满足6项假设：假设1：观测变量为连续变量，如本研究中的成绩为连续变量。

假设2：观测变量可分为2组，如本研究中分为男生和女生。

假设3：观测值之间相互独立，如本研究中各位研究对象的信息都是独立的，不存在相互干扰。

假设4：观测变量不存在显著的异常值。

假设5：观测变量在各组内接近正态分布。

假设6：两组的观测变量的方差相等。

假设1-3取决于研究设计和数据类型，本研究数据符合假设1-3。

那么应该如何检验假设4-6，并进行独立样本t检验呢？三、SPSS操作假设4和假设5可通过以下方式检验。

假设6的检验结果可在结果解释部分查看。

3.1 检验假设4：观测变量不存在显著的异常值在主界面点击Analyze→Descriptive Statistics→Explore，弹出Explore对话框，如图2。

在对话框中将score变量放入Dependent List栏，并将gender变量放入 Factor List栏。

图2 Explore点击Plots，取消对Descriptive栏内 Stem-and-leaf选项的选择，并点击Normality plots with tests选项，点击Continue→OK。

如图3。

图3 Explore: Plots 经上述操作，SPSS输出箱式图。

如图4。

图4 箱式图SPSS中，数据点与箱子边缘的距离大于1.5倍箱身长度，则定义为异常值，以圆点（°）表示；与箱子边缘的距离大于3倍箱身长度，则定义为极端值，以星号（*）表示。

圆点或星号附近的数值是SPSS系统的自动编码（Data View窗口中最左侧蓝色一列中的编码）。

SPSS-比较均值-独立样本T检验案例解析2011-08-26 14:55在使用SPSS进行单样本T检验时，很多人都会问，如果数据不符合正太分布，那还能够进行T检验吗？而大样本，我们一般会认为它是符合正太分布的，在鈡型图看来，正太分布，基本左右是对称的，一般具备两个参数，数学期望和标准方差，即：N(p, Q)如果你的样本数非常少，一般需要进行正太分布检验，检验的方法网上很多，我就不说了下面以“雄性老鼠和雌性老鼠分别注射了某种毒素，经过观察分析，进行随机取样，查看最终老鼠是否活着。

问题：很多人认为，雄性老鼠和雌性老鼠分别注射毒液后，雌性老鼠存活下来的数量会比雄性老鼠多？我们将通过进行统计分析来认证这个假设是否成立。

下面进行参数设置：a 代表：雄性老鼠b代表：雌性老鼠tim 代表：生存时间，即指经过多长时间后，去查看结果0 代表：结果死亡1 代表：结果活着随机抽取的样本，如下所示：打开SPSS- 分析---检验均值---独立样本T检验，如下图所示：将你要分析的变量，移入右边的框内，再将你要进行分组的变量移入“分组变量”框内，“组别group（）里面的两个参数，不能够随意设置，必须要跟样本里面的数字一致点击确定后，分析结果，如下所示：从组统计量可以看出，雄性老鼠的存活下来的均值为0.73，但是雌性老鼠存活下来的均值为1.00，很明显，雌性老是存活下来的个数明显比雄性老鼠多，但是一般我们不看这个结果，为什么？因为样本不够大，如果将样本升至10000个？也许这个均值将会发生变化，不具备统计学意义，我们一般只看独立样本检验的结果。

独立样本检验，提供了两种方法：levene检验和均值T检验两种方法Levene检验主要用来检验原假设条件是否成立，（即：假设方差相等和方差不相等两种情况）如果SIG>0.05，证明假设成立，不能够拒绝原假设，如果SIG<0.05，证明假设不成立，拒绝原假设。

进行levene检验结果判断是第一步，从上图，可以看出 sig<0.05 方差相等的假设不成立，所以看第二行，方差不相等的情况sig=0.082>0.05 即说明 P 值大于显著性水平，不应该拒绝原假设：即指：雌性老鼠和雄性老鼠在注射毒液后，存活下来的个数没有显著的差异本次分析的结果，不支持，很多人认为的：雄性老鼠和雌性老鼠分别注射毒液后，雌性老鼠存活下来的数量会比雄性老鼠多的结论。

SPSS-比较均值-独立样本T检验案例解析2011-08-26 14:55在使用SPSS进行单样本T检验时，很多人都会问，如果数据不符合正太分布，那还能够进行T检验吗？而大样本，我们一般会认为它是符合正太分布的，在鈡型图看来，正太分布，基本左右是对称的，一般具备两个参数，数学期望和标准方差，即：N(p, Q)如果你的样本数非常少，一般需要进行正太分布检验，检验的方法网上很多，我就不说了下面以“雄性老鼠和雌性老鼠分别注射了某种毒素，经过观察分析，进行随机取样，查看最终老鼠是否活着。

问题：很多人认为，雄性老鼠和雌性老鼠分别注射毒液后，雌性老鼠存活下来的数量会比雄性老鼠多？我们将通过进行统计分析来认证这个假设是否成立。

下面进行参数设置：a 代表：雄性老鼠b代表：雌性老鼠tim 代表：生存时间，即指经过多长时间后，去查看结果0 代表：结果死亡1 代表：结果活着随机抽取的样本，如下所示：打开SPSS- 分析---检验均值---独立样本T检验，如下图所示：将你要分析的变量，移入右边的框内，再将你要进行分组的变量移入“分组变量”框内，“组别group（）里面的两个参数，不能够随意设置，必须要跟样本里面的数字一致点击确定后，分析结果，如下所示：从组统计量可以看出，雄性老鼠的存活下来的均值为0.73，但是雌性老鼠存活下来的均值为1.00，很明显，雌性老是存活下来的个数明显比雄性老鼠多，但是一般我们不看这个结果，为什么？因为样本不够大，如果将样本升至10000个？也许这个均值将会发生变化，不具备统计学意义，我们一般只看独立样本检验的结果。

独立样本检验，提供了两种方法：levene检验和均值T检验两种方法Levene检验主要用来检验原假设条件是否成立，（即：假设方差相等和方差不相等两种情况）如果SIG>0.05，证明假设成立，不能够拒绝原假设，如果SIG<0.05，证明假设不成立，拒绝原假设。

进行levene检验结果判断是第一步，从上图，可以看出 sig<0.05 方差相等的假设不成立，所以看第二行，方差不相等的情况sig=0.082>0.05 即说明 P 值大于显著性水平，不应该拒绝原假设：即指：雌性老鼠和雄性老鼠在注射毒液后，存活下来的个数没有显著的差异本次分析的结果，不支持，很多人认为的：雄性老鼠和雌性老鼠分别注射毒液后，雌性老鼠存活下来的数量会比雄性老鼠多的结论。