spss 单样本t检验操作步骤

依据调查问卷，进行单样本T检验SPSS
操作步骤
本文档将介绍如何使用SPSS进行单样本T检验，以便根据调查问卷数据进行统计分析。

步骤一：准备数据
1. 打开SPSS软件并导入数据文件。

2. 确保数据文件中包含了需要分析的目标变量。

步骤二：进行单样本T检验
1. 点击菜单栏中的"分析（Analyse）"选项。

3. 将目标变量拖动到"因变量"栏中，并将参照组变量（在这里通常是一个常数）拖动到"因子"栏中。

4. 点击"确定（OK）"按钮。

步骤三：查看结果
1. 在SPSS输出窗口中，查找单样本T检验的结果。

2. 结果中将显示均值、标准误差、95%置信区间、T值和P值
等统计信息。

请注意，进行单样本T检验前需要确保数据满足一些前提条件，例如正态分布和同方差性。

如果数据不满足这些条件，可能需要使
用非参数测试方法进行分析。

以上是依据调查问卷进行单样本T检验的SPSS操作步骤。

希
望本文档能够帮助您进行统计分析。

spss单一样本的T检验SPSS是一款广泛使用的统计软件，可以用于各种统计分析，包括单一样本的T 检验。

下面是关于如何使用SPSS进行单一样本的T检验的详细步骤和解释。

一、目的单一样本的T检验主要用于比较一个样本的平均值与已知的或预设的数值，或者用于比较一个样本与已知的或预设的数值之间的差异。

这种检验通常用于检验一个样本是否显著地不同于已知的或预设的数值。

二、步骤1.打开SPSS软件，点击“分析”菜单，然后选择“比较平均值”>“独立样本T检验”。

2.在弹出的对话框中，将左侧的“独立样本T检验”选项卡中的“变量”字段拖到右侧的“变量”框中。

3.在“独立样本T检验”选项卡下方的“组”字段中输入已知的或预设的数值。

4.点击“确定”按钮，SPSS将计算并显示T检验的结果。

三、结果解释单一样本的T检验的结果通常包括T值和p值。

T值是计算出的统计量，而p 值是观察到的数据与零假设之间的不一致程度。

如果p值小于选择的显著性水平（通常为0.05），则可以拒绝零假设，认为样本平均值与已知的或预设的数值之间存在显著差异。

四、注意事项1.单一样本的T检验的前提是数据符合正态分布。

如果数据不符合正态分布，可以使用非参数检验，例如Mann-Whitney U检验或Wilcoxon符号秩检验。

2.在使用单一样本的T检验时，需要明确知道或预设的数值是什么，以及为什么要比较这个数值。

如果不知道或预设的数值是什么，或者比较的目的不明确，那么这种检验可能会没有意义或者导致错误的结论。

3.单一样本的T检验只能告诉我们一个样本的平均值与已知的或预设的数值之间的差异是否显著，但不能告诉我们这种差异的实际意义或影响。

因此，在解释结果时需要谨慎，并考虑实际应用背景。

4.在进行单一样本的T检验时，需要确保数据的质量和准确性。

如果数据存在缺失、异常值或错误，将会对结果产生影响。

在进行统计分析前，需要对数据进行清洗和预处理。

5.在进行单一样本的T检验时，需要考虑变量的类型和测量尺度。

SPSS问卷分析篇之单样本T检验
【引入】T检验在问卷分析中经常用到，尤其是通过李克特五级量表收集到的调查数据。

比如：非常同意5、基本同意4、不能确定3、不太同意2、非常不同意1，收集到的数据都是1-5的离散值，还有诸如非常满意、比较满意、不满意等等。

很容易发现一个问题，那就是五级量表中间值是3，如果我们的汇总结果能够显著与3不同，那我们的调查基本上是由意义的。

也就是说，我们要判断一组数据是否显著不同于3，这个时候，就要用的单样本T检验。

【源数据】假设我们已经通过李克特五级量表收集并整理好一份调查数据，包括个性服务、服务态度、促销活动、服务流程、总体满意度5个维度。

量表为：非常同意5、基本同意4、不能确定3、不太同意2、非常不同意1。

现在需要做的是对这5个维度进行评价。

【分析过程】提前求出每份问卷5个维度的均值，再进行SPSS单样本T检验。

第一：在SPSS中选择T检验，需要检验的常数为3。

第二：结果1
原假设各维度均值与3没有差异，现在p值小于0.01，小概率事件不发生，所以，各维度均值与3有显著不同。

可是各维度均值大于3还是小于3呢？当然希望是大于3！
结果2
看到均值那一列数值了吗？各维度均值都明显大于3，这下放心了吧。

说明个性服务、服务态度、促销活动、服务流程还都是可以接受的，较认同，总体满意度4.4，说明我们的各方面的服务已经深得民心，不过，仍需做到最好。

实习三数值变量资料的统计推断（一）第185～199页一、均数的抽样误差及总体均数可信区间的估计（一）均数的抽样误差1.定义在抽样研究中，由于抽样造成的样本均数与总体均数之间的差异或者样本均数之间的差异，称为均数的抽样误差（sampling error）。

抽样误差是不可避免的，造成抽样误差的根本原因是个体变异的客观存在。

（一）均数的抽样误差2.计算一、均数的抽样误差及总体均数置信区间的估计3.性质（1）抽样误差的大小，即标准误，与标准差成正比，与样本含量的平方根成反比。

（2）在实际工作中，减小抽样误差的有效方法是增大样本含量。

标准误的精确值标准误的估计值（二）t分布一、均数的抽样误差及总体均数置信区间的估计（二）t分布2.性质一组与自由度ν有关的曲线，随着自由度ν的增大接近标准正态分布。

一、均数的抽样误差及总体均数置信区间的估计（三）总体均数95％置信区间的估计二、数值变量资料的假设检验(t 检验和z 检验)（一）假设检验的目的推断两个总体均数是否相等（双侧检验：μ1=μ2？，单侧检验：μ1>μ2？或者μ1< μ2？）（二）假设检验方法的选择¾根据σ是否已知以及n的大小，选择t检验或z检验。

¾根据不同的研究设计类型，选择不同的方法。

¾注意单侧、双侧检验的选择*资料中σ已知时，可以用σ代替公式中相应的s 。

t 检验和z检验的应用条件和计算公式（二）假设检验方法的选择二、数值变量资料的假设检验(t 检验和z 检验)二、数值变量资料的假设检验(t 检验和z 检验)（二）假设检验方法的选择完全随机设计的两样本均数的t检验¾假设检验的P 值不能反映总体均数差别的大小。

P 值越小，越有理由（越有把握）认为两总体均数不相等。

¾假设检验的结论具有概率性。

H 0原本正确, 但P ≤0.05，拒绝H 0：第一类错误（α）H 0原本不正确,但P >0.05，不拒绝H 0：第二类错误（β）α为事先指定的检验水平（一般取0.05），β未知；α越小，β越大；α越大，β越小；增大样本量n ，可以同时减小α和β。

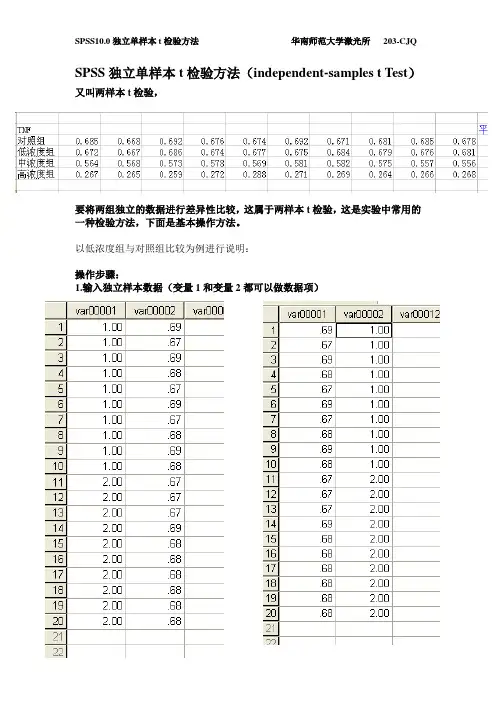
SPSS独立单样本t检验方法（independent-samples t Test）又叫两样本t检验，
要将两组独立的数据进行差异性比较，这属于两样本t检验，这是实验中常用的一种检验方法，下面是基本操作方法。

以低浓度组与对照组比较为例进行说明：
操作步骤：
1.输入独立样本数据（变量1和变量2都可以做数据项）
2.选用程序
从菜单选择Analysize——Compare Mean——Independent-samples t Test,打开对话框，分别将数据变量组和组别变量组对应的var转入右边对应的空白框中，数据变量组转到Test Variable(s),组别变量组转到Grouping Variable
转入后，在定义组别，
点击Difine Groups…按钮，出现如下对话框，然后输入对应的组别号，在这个例子中，group1是用1来表示的，group2使用2表示的。

因此，分别输入1和2，再点击Continue按钮。

点击continue按钮后出现如下对话框，再点击OK，这样独立样本T检验程序定义完成。

3.结果分析
在第二步最后点击OK后，软件的分析结果就会出现，如下图，红框里就是要的数据。

经Levene’s方差齐性检验，F=4.655，而P=0.045<0.5,认为两组总体方差是齐的，就看两样本t检验的第一横列的值（也就是跟F同列的值）：t=1.353，P=0.193，按P=0.05水准，P>0.05,则两样本物显著性差异，P<0.05,有显著性差异，P<0.01时，两样本有极大差异。

如果F的P>0.5，则认为两样本总体方差不齐，则看第二横列的值，t检验的P值分析同上。

在统计学中，我们往往从样本的特性推知随机变量总体的特性。

但由于总体中个体之间存在差异，样本的统计量和总体的参数之间往往会有误差。

因此，均值不相等的样本未必来自不同分布的总体，而均值相等的样本未必来自有相同分布的总体。

也就是说，如何从样本均值的差异推知总体的差异，这就是均值比较的内容。

SPSS提供了均值比较过程，在主菜单栏单击“Analyze”菜单下的“Compare Means”项，该项下有5个过程，如图4-1。

平均数比较Means过程用于统计分组变量的的基本统计量。

这些基本统计量包括：均值（Mean）、标准差(Standard Deviation)、观察量数目(Number of Cases)、方差(Variance)。

Means过程还可以列出方差表和线性检验结果。

[例子]调查了棉铃虫百株卵量在暴雨前后的数量变化，统计暴雨前和暴雨后的统计量，其数据如下：暴雨前 110 115 133 133 128 108 110 110 140 104 160 120 120暴雨后 90 116 101 131 110 88 92 104 126 86 114 88 112该数据保存在“DATA4-1.SAV”文件中。

1）准备分析数据在数据编辑窗口输入分析的数据，如图4-2所示。

或者打开需要分析的数据文件“DATA4-1.SAV”。

图4-2 数据窗口2）启动分析过程在SPSS主菜单中依次选择“Analyze→Compare Means→Means”。

出现对话框如图4-3。

图4-3 Means设置窗口3）设置分析变量从左边的变量列表中选中“百株卵量”变量后，点击变量选择右拉按钮，该变量就进入到因子变量列表“Dependent List:”框里，用户可以从左边变量列表里选择一个或多个变量进行统计。

从左边的变量列表中选中“调查时候”变量，点击“Independent List”框左边的右拉按钮，该变量就进入分组变量“IndependentList”框里，用户可以从左边变量列表里选择一个或多个分组变量。

使用“住房状况调查”数据，对不同性别、户口状况的居民现住面积进行独立样本T检验并解释其结果。

答：对不同性别的居民现住面积进行独立样本T检验：①SPSS操作：第一步：点击“分析”、依次选择“比较平均值”、“独立样本T检验”；第二步：将“现住面积”选入“检验变量”，“性别”选入“分组变量”，在点击“定义组”，在“组1”中键入1，在“组2”中键入2，点击“继续”、“确定”。

②结果输出：③结果解读：先用F检验对不同性别的居民现住面积的方差是否向相等加以验证，然后利用t检验对不同性别的居民现住面积的均值是否存在差异进行检验。

从独立样本检验输出图中可以看到：F统计量为1.598，p值为0.206，在显著性水平0.05下，p值大于0.05，不拒绝原假设，即认为不同性别的居民现住面积的方差相等，没有差别。

由于不同性别的居民现住面积的方差没有差别，t检验将看假定等方差一栏。

t统计量为2.982，p值为0.003，在显著性水平0.05下，p值小于0.05，拒绝原假设，即认为不同性别的居民现住面积的均值有显著性差异。

对不同户口状况的居民现住面积进行独立样本T检验：④SPSS操作：第一步：点击“分析”、依次选择“比较平均值”、“独立样本T检验”；第二步：将“现住面积”选入“检验变量”，“户口状况”选入“分组变量”，在点击“定义组”，在“组1”中键入1，在“组2”中键入2，点击“继续”、“确定”。

⑤结果输出：⑥结果解读：先用F检验对不同户口状况的居民现住面积的方差是否向相等加以验证，然后利用t检验对不同户口状况的居民现住面积的均值是否存在差异进行检验。

从独立样本检验输出图中可以看到：F统计量为5.966，p值为0.015，在显著性水平0.05下，p值小于0.05，拒绝原假设，即认为不同户口状况的居民现住面积的方差存在显著差异。

由于不同户口状况的居民现住面积的方差存在显著差异，t检验将看不假定等方差一栏。

t统计量为3.314，p值为0.001，在显著性水平0.05下，p值小于0.05，拒绝原假设，即认为不同户口状况的居民现住面积的均值有显著性差异。

spss操作独立样本T检验模板.doc一、独立样本T检验的基本概念独立样本T检验是指用于比较两个独立样本平均数是否有显著差异的统计方法。

其中，独立样本是指两组样本各自独立，互不干扰，不相关的情况。

例如，对于两组人员，第一组接受了药物治疗，第二组未接受药物治疗，比较两组人员的体重是否有差异。

在这个例子中，两组人员是独立的。

二、SPSS独立样本T检验的操作步骤（一）数据收集导入在进行独立样本T检验之前，需要先确定要对比的两组数据，并将数据收集起来。

将数据按不相同的组别（如服用药物和未服用药物）分别输入到SPSS中，分别为组别A和组别B。

（二）前期处理在开始分析之前，需要先做一些数据预处理工作，包括数据清洗、离群值检查和变量分布及可视化统计分析等。

（三）执行独立样本T检验1. 打开SPSS，依次选择"分析"-"比较均值"-"独立样本T检验"。

2. 将需要检验的变量（如体重）拖到"测试变量列表中"栏位中。

3. 选择独立样本的两个组别（如A组和B组），将其拖到独立样本列表（"样本1"和"样本2"）中。

4. 选择置信度（Confidence Interval）和显著性水平（Significance Level）。

5. 点击"OK"，等待SPSS自动为我们生成结果。

（四）检验结果解释SPSS生成的独立样本T检验结果包括了三个表格，分别是"平均数和标准误"、"独立样本T检验"和"效应大小"。

1. "平均数和标准误"表格：这个表格显示了每一组别数据的均值（Mean）和标准误（Standard Error），同时还包括组别的样本量（N）和方差（Variance）等信息。

2. "独立样本T检验"表格：这个表格包含了检验结果的详细信息，包括了统计学指标（如t值和P值）、置信区间（Confidence Interval）和自由度（Degrees of Freedom）等信息。

spss单样本t检验Analyze----compare Means----one sample T test输入方式实验数据121212123456495直接输入数据Sig=0.000 差异显著独立样本t检验（两组数据）Analyze-----compare Means----Independent-samples T test 输入方式试验分组实验数据1 121 131 121 121111222222222两组数据个数可以不同成组数据t检验Analyze----compare Means-----paired-samples T test单因素方差分析Analyze---compare means----one-way ANOVA(analyze of variance)Factor （因素）1 1 1 1 1 2 2 2 2 2 2 3 3 3 3(分组)Dependent List 试验数据polynomial linescontrast---polynomial---Degree---linearpost Hoc Multiple comparisons-----LSD(Duncan 邓肯检验) 先选方差齐性在结果中判断Sig值？＜0.05（差异显著）若不齐则进行数据转化。

数据输入分组试验数据1 121 131 1311222222333333444444双因素方差分析Analyze-----General linear Model-----univariateDependent Variable(因变因素)因别的数字变化而变化Fixed Factor （固定因素）Random Factors(随机因素)Model-----custom-----Build Term---Interaction(交互作用)----Main effects（主因素）Contrast--- simple---first----changePlot Hoc----LSD (Duncan)Univariate Options----Homogeneity tests(方差齐性分析) Display Means for （协方差使用）钙镁增重1 11 11 11 21 21 21 31 31 31 41 41 42222222222相关性分析Anlyze---correlation----bivariate输入格式Pearson----皮尔逊检验Two-tailed 双尾Pearson correlation 相关系数=0.433 表明相关性不大Sig（2-tailed）双尾p值>0.05 差异不显著一般p>0.6 sig<0.05时两组数据显著相关（不同专业可能要求不同）回归分析Anlyze----regression---curve estimation(曲线)Dependent---因变量Independent---自变量（独立—不依靠别的数据自己变化）Linear—直线型Quadratic---二次型Compound---复合函数Growth—生长曲线Logarithmic—对数函数Cubic---三次函数S---s型曲线Exponential----指数函数Inverse 倒数函数Power---幂函数Logistic 逻辑函数直线在y轴上的截距不能是负值，因为到时候代入试验数据时会出现负值单变量协方差分析Anlyze—General Linear Model—univariateModel—custom 主变量与协变量分别以main effects选入Contrast---simple---first 点击changeOption中选择分析变量放入display means for 然后选择compare main effects Display中选择homogeneity test（方差齐性分析）Sig=0.125>0.05 方差齐性初重表示选择的初始个体中的初重差异性大（0.039<0.05）Factor中的数据已经出去了差异显著的数据LSD检验OriginA表示x自变量B表示y因变量Analysis---fitting---Nonlinear curve fit（ctrl+y）Function selection—方程选择Category 分类Function方程Code 方程一般表达式Parameters 参数（当a为定值时在fixed中打钩然后填a值若无则可不填一般给初始值1）若方程没有可自己设置Category中选择user definedFunction—new写好后fit（参数形式一定要一样）十二、施工方案（一）工程概述本工程为深圳中心机房楼，是由深圳市科技工贸和信息化委员会投资兴建，由中国中元国际公司设计，该工程位于深圳市南山西丽大学城区。

独立样本t检验spss的步骤独立样本t检验SPSS的步骤概述：独立样本t检验（Independent Samples t-test）是一种常见的统计方法，用于比较两组独立样本的均值是否存在显著差异。

在SPSS （Statistical Package for the Social Sciences）软件中进行独立样本t检验是一项相对简单而又方便的任务。

本文将详细介绍如何使用SPSS进行独立样本t检验的步骤。

步骤一：准备数据和SPSS环境在进行独立样本t检验之前，首先需要准备好需要进行比较的两组数据以及将其输入到SPSS软件中。

确保数据的格式正确，即每一组数据都应该是一个单独的变量。

打开SPSS软件，并在数据编辑器中将这两组数据输入到不同的变量列中。

步骤二：指定假设在进行独立样本t检验之前，需要明确要比较的两组数据的假设。

独立样本t检验有一对假设需要检验，分别是零假设（H0）和备择假设（H1）。

零假设（H0）：两组数据的均值相等。

备择假设（H1）：两组数据的均值不相等。

步骤三：进行独立样本t检验在SPSS软件中，进行独立样本t检验需要使用“Analyze”和“Compare Means”菜单。

按照以下步骤进行操作：1. 选择菜单栏中的“Analyze”。

2. 选择“Compare Means”。

3. 在“Compare Means”菜单下，选择“Independent-Samples T Test”。

在弹出的对话框中，将需要比较的两组数据变量选择到“Test Variables”框中。

点击“箭头”按钮将其移至“Grouping Variable”框中。

点击“OK”按钮，SPSS将自动为你进行独立样本t检验，并生成相应的结果报告。

步骤四：解读结果SPSS生成的独立样本t检验结果报告包含了一些关键的统计信息。

以下是一些常见的结果：1. “Mean Difference”（平均数差异）：表示两组数据均值之间的差异。

第5章单样本T检验
1.从菜单栏中选择Analyze分析→Compare Means比较均值→One-Sample t Test单样本T检验
2.打开单样本T检验对话框，变量hoursweek出现在对话框左边
3.选择因变量hoursweek，点击向右箭头，将变量移到Test Variable 检验变量框
4.将检验值输入框输入52，这个是原假设的指定值，这个很关键，特别容易出现错误。

在spss实施单样本t检验时，确保检验值是原假设的指定值。

5.点击ok确认
结果解释：
单个样本统计量
N 均值标准差均值的标准误hoursweek 16 59.0000 7.14609 1.78652
单个样本检验
检验值 = 52
t df Sig.(双
侧) 均值差
值
差分的 95% 置信
区间
下限上限
hoursweek 3.918 15 .001 7.00000 3.1921 10.8079
P值0.001<0.05，因此拒绝原假设。

均值差值7，说明知名会计事务
所每周平均工作时间（59）与原假设中的指定值52的差。

结果呈现方式：
均值M 标准差SD Hoursweek
59.0
7.15**
在知名会计师事务所的雇员（M=59.0，SD=7.15）每周工作时间显著多于52个小时的全国平均水平，t(15)=3.92, p<0.05, d=0.98
98
.015
.77d ===标准差差样本均值与总体均值之。

单样本t检验-SPSS教程一、问题与数据某研究者拟开展一项健康调查，在开展该研究之前，他想了解所招募的40名研究对象的体重指数BMI是否具有代表性。

根据既往研究报道，目标人群的BMI 均值为24kg/m²。

该研究者想知道他招募的研究对象的BMI均值是否也为24kg/m²。

部分数据图1。

图1 部分数据二、对问题分析研究者拟分析样本均值与总体均值是否不同，即判断招募研究对象的BMI均值与总体人群BMI均值24之间是否有差异。

针对这种情况，可以使用单样本t 检验，但需要先满足4项假设：假设1：观测变量为连续变量，如本研究中的BMI为连续变量。

假设2：观测值相互独立，如本研究中各位研究对象的信息都是独立的，不存在相互干扰作用。

假设3：观测变量不存在显著的异常值。

假设4：观测变量接近正态分布。

假设1和假设2取决于研究设计和数据类型，本研究数据符合假设1和假设2。

那么应该如何检验假设3和假设4，并进行单样本t检验呢？三、SPSS操作3.1 检验假设3：观测变量不存在显著的异常值在主界面点击Analyze→Descriptive Statistics→Explore，在Explore对话框中，将变量BMI选入Dependent List。

在Display模块内点击Plots。

如图2。

图2 Explore点击Plots，出现Explore: Plots对话框，保留Boxplots内系统默认选项Factor levels together，在Descriptive内取消选择Stem-and-leaf，在下方勾选Normality plots with tests。

点击Continue→OK。

如图3。

图3 Explore: Plots经上述操作，SPSS输出箱式图，研究者可根据箱式图判断数据中是否存在异常值。

如图4。

图4 箱式图SPSS中，数据点与箱子边缘的距离大于1.5倍箱身长度，则定义为异常值，以圆点（°）表示；与箱子边缘的距离大于3倍箱身长度，则定义为极端值，以星号（*）表示。