恒定磁场的基本方程
- 格式:pdf
- 大小:319.78 KB
- 文档页数:10

恒定磁场基本方程的微分形式引言恒定磁场是指磁场中磁感应强度、磁场强度、磁场偏转角等参数在时间和空间上均保持不变的情况。
恒定磁场具有许多重要应用,例如电动机、发电机、磁共振成像等。
为了深入了解恒定磁场的基本方程,需要进行微分形式的推导和讨论。
恒定磁场基本方程在恒定磁场中,我们可以根据安培定律推导出磁场的基本方程。
安培定律表明,在闭合回路中,电流周围的磁场的环绕方向是闭合回路上的电流方向,其磁感应强度大小与电流大小成正比。
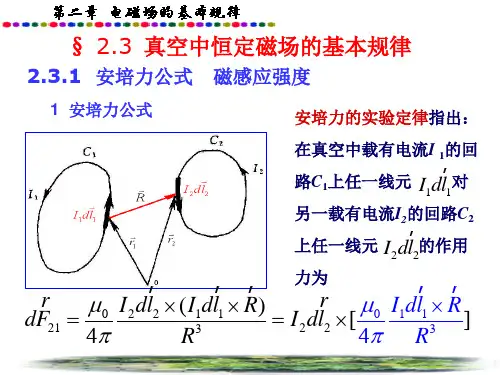
根据安培定律,我们可以得到恒定磁场的基本方程的微分形式:1. 电流元在磁场中受到的磁场力表达式为:dF =I (dl ×B ),其中dF 表示电流元受力的微元,I 表示电流,dl 表示电流元的微元长度,B 表示磁感应强度。
2. 根据叉乘的性质,可以得到上式的分量形式:{dF x =I(B z dy −B y dz)dF y =I (B x dz −B z dx )dF z =I(B y dx −B x dy)3. 利用矢量分析中的散度和旋度概念,可以进一步将上述方程转化为微分形式:{ ∂B x ∂x +∂B y ∂y +∂B z ∂z =0∂B x ∂t =0∂B y ∂t =0∂B z ∂t =0上述方程描述了恒定磁场的基本特性,其中第一个方程表示磁场的无源性,即磁感应强度的散度为零;后三个方程表示磁场随时间不变,即磁感应强度对时间的偏导数为零。
恒定磁场中的应用和意义恒定磁场具有许多重要的应用和意义,下面将从以下几个方面进行讨论:1. 电动机和发电机在电动机和发电机中,恒定磁场被用于产生磁场,从而实现电动机的旋转和发电机的电能转换。
利用恒定磁场的基本方程,可以对电动机和发电机的性能进行分析和优化。
2. 磁共振成像磁共振成像(MRI)是一种利用恒定磁场和变化磁场的共同作用原理进行医学影像诊断的技术。
MRI利用恒定磁场对人体组织中的原子核进行定向,然后通过应用变化磁场使原子核进入共振状态,进而通过检测共振信号获得影像信息。





恒定磁场基本方程的微分形式为恒定磁场基本方程的微分形式为什么重要?磁场是物理学中的一个重要概念,它与电场一起构成了电磁场。
在恒定磁场中,磁感线是直线或圆弧,而且磁感线的密度相等。
恒定磁场的基本方程可以用来描述磁场的性质和行为,因此它是理解和应用磁场相关知识的基础。
一、什么是恒定磁场?恒定磁场指在空间某个区域内,时间不变或者时间变化很缓慢,且空间各点处的磁感应强度大小、方向都不随时间改变或者改变很小。
在这种情况下,我们可以使用静电学类比来处理问题。
二、什么是恒定磁场基本方程?1. 定义根据安培环路定理(又称安培第二定律),在任何闭合回路上,通过该回路的电流总和等于该回路所包围区域内的总电流。
在恒定磁场中,该定理可以表示为:∮B·dl = μ0I其中B表示磁感应强度(单位:特斯拉),l表示回路的长度,I表示通过该回路的电流(单位:安培),μ0表示真空中的磁导率(单位:亨利/米)。
2. 微分形式根据斯托克斯定理,一个闭合曲线所包围的面积内的旋度等于该曲线沿着法向方向的环流密度。
在恒定磁场中,该定理可以表示为:∇×B = 0其中∇表示偏微分算子,×表示向量积运算。
将斯托克斯定理应用于一个无限小的闭合回路上,则有:∮B·dl = ∫(∇×B)·dS其中dS表示曲面元素面积。
由于恒定磁场中磁感应强度不随时间变化,因此我们可以将上式简化为:∇×B = 0这就是恒定磁场基本方程的微分形式。
三、为什么恒定磁场基本方程的微分形式重要?1. 描述磁场性质恒定磁场基本方程的微分形式可以用来描述恒定磁场的性质和行为。
它告诉我们,在恒定磁场中,任何一个点处的旋度等于零。
这意味着在任何一点处,磁场的方向是唯一的,因为不存在旋转的磁场线。
这也意味着磁场是无源场,即不存在产生磁场的电荷或电流。
2. 解决问题恒定磁场基本方程的微分形式可以用来解决一些与恒定磁场相关的问题。

第 4 章恒定磁场4.2 真空中恒定磁场的基本方程应用举例半径为 a 的无限长直导体圆柱均匀通过电流 I ,计算导体内外的B 。
解: ⑴ 电流分布具有轴对称性,选柱坐标⑵ 分析磁场的分布 zaI⑶ 沿磁感应线取B 的线积分沿ϕ 方向 ∑⎰==∙I B c02d μπρl B ρ ≤ a 时222aIJ I ρπρ==∑2022022aI a I B πρμρπρμϕ==∴ρ ≥ a 时πρμϕ20IB =II =∑例1两相交圆柱,半径同为a ,轴线相距 c ,通过强度相等方向相反的电流 I ,因而相交部分J = 0。
证明相交区域是匀强磁场。
证: ⑴ 两圆柱单独存在时,均具有轴对称性,选两套柱坐标 ⑵ 计算相交区域任取一场点P 的磁感应 22101d a Icρμ=∙⎰l B 201221101221a I a I z πμρπρμϕρa a B ⨯==22202d aIcρμ=∙⎰l B2022222022)(22aI a I z πμρπρμϕρa a B ⨯-=-=202020*******)(a Ica I a I yz z πμπμπμa c a ρρa B B B =⨯=-⨯=+=例2 O 1 O 2 Pρ1 ρ2 ⊗ ⊙ I Iz x无限大平面上均匀分布面电流J s ,求距此平面 r 处的磁感应B 。
解: ⑴ 电流分布具有平面对称性,选直角坐标。
设J s = a z J s⑵ x >0,磁场方向沿 +y 轴;x <0,磁场方向沿 –y 轴⑶ 在xOy 上选取图示矩形回路lJ l B cs 02d μ==∙⎰l B 2s0J B μ=例 0, 20>x J y sa μ0, 20<-x J y sa μ=B z xy J zz xy J zl。


恒定磁场的基本方程和边界条件1. 嘿,你知道恒定磁场不?它的基本方程就像一把神奇的钥匙呢。
就好比你要打开一扇神秘的门,这方程就是开锁的关键。
高斯定理说通过任意闭合曲面的磁通量恒等于零。
比如说,你想象一个完全封闭的盒子,磁场线就像一些调皮的小虫子,它们进进出出这个盒子,但总体数量不会有变化,既不会凭空多出来,也不会无端消失。
这多有趣呀,感觉磁场就像一个有秩序的小世界。
2. 恒定磁场的安培环路定理也很厉害哦。
这就像在一个迷宫里找路,磁场强度沿着闭合路径的线积分等于穿过这个路径所围面积的电流的代数和的μ₀倍。
打个比方,假如电流是一群奔跑的小怪兽,磁场强度就是跟着它们跑的小尾巴。
你看那些电线里的电流在流动的时候,周围就会产生磁场,这个磁场就按照安培环路定理的规则存在着。
你说神奇不神奇?3. 那恒定磁场的边界条件又是怎么回事呢?这就像两个不同的国家之间的边境规则。
在两种不同磁介质的分界面上,磁场强度的切向分量是连续的。
就好像两个人在边境上握手,虽然两边的情况可能有些不同,但这握手的力度(切向分量)是一样的。
比如说,一块铁和空气的交界处,磁场强度的切向部分不会突然变个样。
4. 再说说磁感应强度的法向分量吧。
在两种磁介质的分界面上,磁感应强度的法向分量满足一定的关系。
这就像两个相邻的池塘,水面高度(类比法向分量)有一定的关联。
假如一个池塘里的水涨一点,另一个池塘也会受到影响。
就像在磁介质中,一边的磁感应强度的法向分量改变了,另一边也会跟着有相应的变化。
这是不是很像一种默契呢?5. 你可别小瞧这些恒定磁场的方程和边界条件啊。
它们就像魔法咒语一样,掌控着磁场这个神秘的魔法世界。
你想啊,如果没有这些规则,磁场就像一群没头的苍蝇,到处乱撞。
就像一个没有交通规则的城市,汽车到处乱开,那可就乱套了。
而这些方程和条件就是磁场世界的交通规则,让一切井井有条。
6. 我跟你讲,理解这些就像解开一个超级有趣的谜题。
就像玩拼图,每一块都很重要。
恒定磁场基本方程的微分形式
恒定磁场基本方程的微分形式是指表达磁场变化率的一种方程形式,其中包括了磁场的旋度和磁场随时间变化的导数。
在电磁学领域中,磁场是一种非常重要的物理量,它与电场一起构成了电磁场,是电磁学理论的基础之一。
恒定磁场指的是磁场在时间上不发生改变的情况,因此可以将磁场看做是一个恒定的场。
对于恒定磁场,其基本方程可以表示为:
∇×B = μ0J
其中,B是磁场,J是电流密度,μ0是真空中的磁导率,∇×表示旋度运算符。
这个方程表达了磁场的旋度与电流密度之间的关系,可以通过旋度运算符来求解。
旋度运算符是一个矢量运算符,用于计算一个矢量场的旋度。
它将一个矢量场的偏导数进行了组合,并给出了一个新的矢量场。
在这个方程中,磁场的旋度表示了磁场的变化率,而电流密度则表示了磁场的来源。
这个方程告诉我们,如果我们知道了磁场的变化率和电流密度,就可以求解出磁场的分布情况。
如果我们考虑磁场随时间的变化,那么可以将上述方程进行扩展,得到恒定磁场基本方程的微分形式:
∇×E = -∂B/∂t
其中,E是电场,B是磁场,∂/∂t表示对时间的偏导数。
这个方程表示了电场的旋度与磁场随时间变化的导数之间的关系。
它告诉我们,如果我们知道了磁场随时间的变化率和电场的旋度,就可以求解出电场的分布情况。
恒定磁场基本方程的微分形式是电磁学中非常重要的一个方程形式。
它将磁场的变化率和电流密度联系起来,以及将电场的旋度和磁场随时间的变化联系起来,为电磁学理论的研究提供了重要的基础。
2-2-5稳恒磁场基本方程因磁场也是矢量场,在第一章中,我们知道,矢量场的基本性质可由它的散度和旋度方程描述。
下面我们导出磁场的基本方程。
对于电流密度分布为J 在空间P (r )点产生的磁通密度为:3(()d 4V V Rμπ'')⨯='⎰J r RB r (2-2-20)用戴尔算符∇点乘上式两边,注意到积分是对源坐标变量,而戴尔算符是对场变量运算。
因此,我们有:0333d d d 444V V V V V V RRRμμμπππ''''⨯'⨯∇=∇'=∇'='∇⨯'⎰⎰⎰J R J RR B J又因为31()0RR∇⨯=∇⨯-∇≡R因此,()0∇=B r(2-2-21a)上式称为磁场中的高斯定理微分形式。
上式表明磁场的散度总是为零,即磁场不存在散度源。
磁场是一无散场。
磁通密度B 通过一有向面积s 的通量称为磁通,记为ψ。
则d sψ=⎰B s磁通的单位为韦伯(Wb)。
正因为此定义,B 称为磁通密度。
由散度定理,式(2-2-21a)的积分形式为:d 0s=⎰ B s (2-2-21b)上式称为磁场中的高斯定理积分形式。
上式说明,稳恒磁场通过任一封闭面的总磁通总是零,即磁场是一管量场。
或说,磁场线总是闭合的,没有起点和终点。
此称为磁通连续性原理。
取式(2-2-20)的旋度得:3(()d 4V V Rμπ'')⨯∇⨯=∇⨯'⎰J r RB r注意积分和算符∇的运算是对不同的变量,上式右边:3322(d d 441()d 4()d 4[()]d 41[()]d 4V V V V V V V V RRV R V RV R RV RRμμππμπμπμπμπ''''''')⨯'⨯∇⨯'=∇⨯'=∇⨯-'⨯∇''=∇⨯∇⨯'''=∇∇-∇'1=∇'∇-'∇'⎰⎰⎰⎰⎰⎰J r R J R J J J J J J因为R = r – r '及11RR∇=-∇'、214()Rπδ∇=-R ,我们得:300(d ()d d 4441()d d ()44V V V V V V V V RRV V R Rμμμπδπππμμμππ'''''')⨯1∇⨯'=∇-'∇''+'4(-')''=∇-∇''+∇∇'''+⎰⎰⎰⎰⎰ J r R J J r r J J J r上式右边第一项可转为封闭面积分,因电流是局限在s '包围的体积V '内,此面积分为零。