正弦交流电的瞬时值、最大值和有效值

交流电压的有效值、平均值和瞬时值引言交流电是我们日常生活中常见的一种电力形式，它具有周期性变化的特点。

在分析交流电时，我们常常关注其有效值、平均值和瞬时值。

本文将对这三个概念进行详细解释，并探讨它们之间的关系。

交流电的特点交流电是指电流和电压随时间变化而周期性地改变方向和大小的电信号。

在交流电中，电流和电压都是随时间而变化的，且其波形通常呈正弦曲线。

有效值（RMS）有效值又称为均方根（Root Mean Square，简称RMS），是衡量交流电大小的一个重要参数。

它表示一个周期内正弦波振幅平方的平均数，并且与相同大小的直流电产生相同效果。

对于一个正弦波来说，其有效值等于其峰-峰值（peak-to-peak value）除以2倍根号2。

峰-峰值即为波形从最低点到最高点所经历的全部变化。

例如，一个正弦波的峰-峰值为10伏特，则其有效值为10 / (2 * √2) ≈ 3.54伏特。

有效值在电力系统中有着重要的应用，例如计算功率、电流负载等。

平均值平均值是指一个周期内交流电信号的平均数。

对于正弦波来说，其平均值为0，因为正弦波在一个周期内上升和下降的部分面积相等。

然而，在实际应用中，我们通常关注交流电信号的绝对值平均数。

这个平均数可以通过将正弦波进行整个周期的积分，并除以一个周期的长度来计算得到。

对于一个正弦波来说，其绝对值平均数等于其有效值乘以根号2 / π。

即：绝对值平均数 = 有效值* √2 / π。

例如，一个正弦波的有效值为3伏特，则其绝对值平均数为3 * √2 / π ≈1.35伏特。

瞬时值瞬时值是指交流电信号在某一时刻的具体数值。

由于交流电信号是随时间变化的，所以瞬时值可以看作是时间的函数。

对于正弦波来说，瞬时值可以表示为：V(t) = Vm * sin(ωt + φ)其中，V(t)表示瞬时值，Vm表示峰值，ω表示角频率，t表示时间，φ表示相位差。

三者之间的关系在一个周期内，交流电信号的瞬时值是不断变化的，而有效值和平均值则是对这些瞬时值进行综合考虑得到的。

交流电的平均值、瞬时值、最大值、有效值1．从交流发电机来看这些概念的实值。

1、发电模式：N 匝线圈，其面积为S ，总电阻为r ，在一匀强磁场中（磁感应强度为B ），绕垂直于B 的轴，以角速度ω匀速转动；即构成交流电源；交流电源通过滑环和电刷引到外电路，即构成交流全电路。

2、概念的理解：A 、最大值，当线圈平面与磁场平行时，出现最大值。

最大电动势Em=NB ωS最大电流Im=rR Em +，R 两端的最大电压Um=I m ·R 。

注意：最大值与线圈的形状、以及转动轴处于线圈平面内哪个位置无关，但转轴应与磁感线垂直。

B 、瞬时值：交流全路中，其电动势、电流、电压、均随时间发生周期性变化，如从中性面开始计时，其瞬时值分别为：e=Emsin ωt i=Imsin ωt u=Umsin ωtC 、有效值：对于正弦（或余弦）交流电，有效值=2最大值 。

有效值也叫均方根值 即 E=2EmI=2ImU=2UmD 、 平均值： 对于某一段时间或某一过程，其平均感应电动势： I t NE 平均电流→∆∆∙=φ=U rR E 平均电压→+=I R ∙ 2、容易出现的错误：（1）有效值的理解：有效值=2最大值，学生容易把条件“正弦或余弦”交流电忽视，对于非正弦或余弦交流电，学生很难建立起电流热效应方程，以求解有效值。

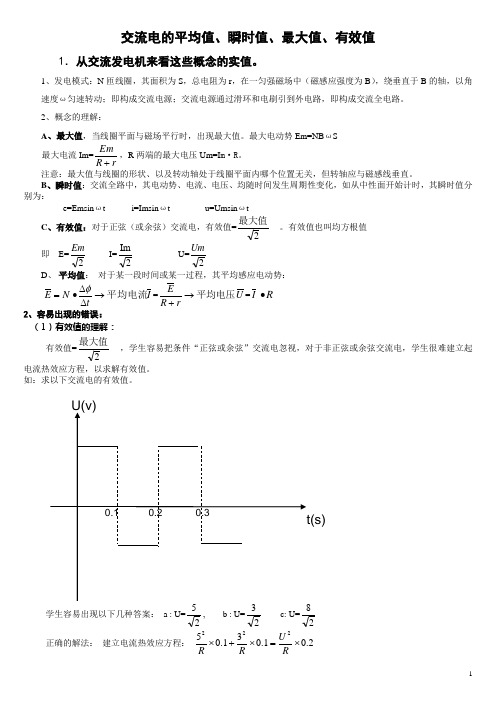
如：求以下交流电的有效值。

学生容易出现以下几种答案： a : U=2, b : U=2 c: U=2正确的解法： 建立电流热效应方程： 2.01.031.05222⨯=⨯+⨯RU R R 即： U=17 （V ）注意：①各种交流用电器上所标的额定电压、电流均指有效值。

②交流电表的示数全为有效值。

③电器元件（如电容）的击穿电压（耐压值）指的是最大值，但保险丝熔断电流为有效值④一般所说交流电的值，均为有效值⑤ 求解交流电产生的热量问题时，必须用有效值，不能用平均值。

⑥中各量均为有效值。

⑦ 若计算通过电路某一截面的电量，需用电流的平均值。

交流电平均值、瞬时值、最大值、有效值林永德在交流电教学中，历届学生对交流电的瞬时值、最大值、有效值、平均值的理解容易出错，有的乱用方式，有的忽视条件，如果在教学中注意以下两个方面，可以有效地防止学生所出的错误。

1．以交流发电模式为主体，揭示概念的实值。

① 发电模式：N 匝线圈，其面积为S ，总电阻为r ，在一匀强磁场中（磁感应强度为B ），绕垂直于B 的轴，以角速度ω匀速转动；即构成交流电源；交流电源通过滑环和电刷引到外电路，即构成交流全电路。

② 概念的理解：A 、最大值，当线圈平面与磁场平行时，出现最大值。

最大电动势Em=NB ωS 最大电流Im=rR Em +，R 两端的最大电压Um=I m ·R 。

B 、瞬时值:交流全路中，其电动势、电流、电压、均随时间发生周期性变化，如从中性面开始计时，其瞬时值分别为：e=Emsin ωt i=Imsin ωt u=Umsin ωtC 、有效值：对于正弦（或余弦）交流电，有效值=2最大值。

即 E=2EmI=2ImU=2UmD 、 平均值： 对于某一段时间或某一过程，其平均感应电动势： I tN E 平均电流→∆∆•=φ=U r R E 平均电压→+=I R • 2、学生容易出现的错误：（1）有效值的理解：有效值=2最大值，学生容易把条件“正弦或余弦”交流电忽视，对于非正弦或余弦交流电，学生很难建立起电流热效应方程，以求解有效值。

如：求以下交流电的有效值。

学生容易出现以下几种答案： a : U=25, b : U=23c: U=28正确的解法： 建立电流热效应方程： 2.01.031.05222⨯=⨯+⨯RU R R 即： U=17 （V ）（2）平均值的理解：如：交流发电模式中，从中性面开始，转过060，求此过程的平均电动势。

学生容易出现以下错误，把平均电动势理解为电动势的平均值，即E =S NB Em e e ω43260sin 02021=+=+ 正确的解法： E =N πωωπφ2326160cos 0S NB BS BS N t =•-=∆∆ （3）求解功率或电热用交流电源给外电路供电，在求解功率或电热问题的时候，学生很容易把平均值与有效值混淆。

教案纸
电压与电流的相位差为：2
)6
(3
πππϕϕϕ=--=-=i u
相位差的存在，表示两个正弦量的变化进程不同。

两个正弦量，根据相位差的不同，可以有以下几种不同的变化进程:
（1）当ϕ= 0，即ϕu = ϕi 时，两个正弦量的变化进程相
同，称为电压u 与电流i 同相；
（2）当ϕ> 0，即
ϕ
u
>
ϕ
i
时，电压u 比电流i 先到达零值
或正的最大值，称电压u 比电流i 在相位上超前ϕ角。

反过来也可以称电流i 比电压u 滞后ϕ角，
（3）当ϕ=2
π
时，两正弦量的变化进程相差90°称它们为正交，
（4）当ϕ=π时，两正弦量的变化进程刚好相反，称它们为反相，
【例题】 已知两正弦电动势分别是:
e 1=100V t )60100sin(2︒+π，e 2V t )30100sin(265︒-=π。

求：（1）各电动势的最大值和有效值；
（2）频率、周期、相位、初相位、相位差； 解：（1）最大值 V Em 21001= V Em 2652= 有效值 V E 1002
21001==
V E 652
2652==
（2）频率
Hz
f
f 50210022
1
===
=
π
π
πω 周期 s f T T 02.050
1
121==== 相位
)60100(1︒+=t πα )30100(2
︒-=t πα
初相位︒=601
ϕ ︒-=302
ϕ
相位差︒=︒--︒=-=
90)30(602
1
ϕ
ϕϕ。

交流电的基本概念交流电可分为正弦交流电和非正弦交流电。

正弦交流电的大小和方向随时间按正弦规律周期性变化，通常所说的交流电就是指正弦交流电。

1. 正弦交流电（1）正弦交流电的产生：正弦交流电由交流发电机产生的。

（2）正弦交流电的三要素①瞬时值、最大值、有效值图1 正弦交流电波形瞬时值：正弦波上每一点的幅度称为正弦交流电的瞬时值，反映该点正弦交流电的大小，用小写字母表示，如i、u分别表示正弦交流电流和正弦交流电压的瞬时值。

峰值：正弦波上幅度最大点的值称为峰值。

峰值有两个，其中一个峰值为正，另一个峰值为负，两者大小相等。

峰-峰值：两个峰值之间的垂直量称正弦交流电的峰-峰值，如图2所示。

峰值的绝对值称正弦交流电的最大值，反映正弦交流电大小变化的范围，用大写字母加下标m表示，如I m、U m分别表示正弦交流电流和正弦交流电压的最大值。

图2 正弦波的峰-峰值有效值：相同时间内、相同电阻上，产生与交流电相同热量所需的直流电的大小。

I＝0.707I m U＝0.707U m一般电气设备上标注的额定电压、额定电流都是指有效值。

当给定或测量交流电压、交流电流时，除非特别说明，也都是指有效值。

大多数仪表都能测量显示交流电压、交流电流的有效值。

②相位角、初相角在实际应用中，正弦波的相位通常用转子线圈旋转了多长时间来表示。

如果1秒钟转子线圈旋转了ω电角度，则t时间正弦波的相位为：Φ＝ωt＋φ其中，Φ称为相位角，φ称为初相角③周期、频率、角频率周期：正弦波完成一次循环所需的时间叫周期，用T表示。

周期的单位是秒（s）。

频率：指1秒钟循环的次数，用f表示。

频率的单位是赫兹（Hz），简称赫。

角频率：指1秒钟变化的电角度，用ω表示，单位是弧度/秒（rad/s）。

关系：2πf（3）正弦交流电的表示三角函数法：u＝U m sin（ωt＋φu）＝U sin（ωt＋φu）i＝I m sin（ωt＋φi）＝I sin（ωt＋φi）波形图表示法：图3 正弦交流电的波形表示2. 三相正弦交流电正弦交流电有单相正弦交流电和三相正弦交流电两种，实际应用中的单相正弦交流电只是三相正弦交流电中的某一相。

交流电平均值、瞬时值、最大值、有效值的区别高中分校 林永德在交流电教学中，历届学生对交流电的瞬时值、最大值、有效值、平均值的理解容易出错，有的乱用方式，有的忽视条件，如果在教学中注意以下两个方面，可以有效地防止学生所出的错误。

1．以交流发电模式为主体，揭示概念的实值。

① 发电模式：N 匝线圈，其面积为S ，总电阻为r ，在一匀强磁场中（磁感应强度为B ），绕垂直于B 的轴，以角速度ω匀速转动；即构成交流电源；交流电源通过滑环和电刷引到外电路，即构成交流全电路。

② 概念的理解：A 、最大值，当线圈平面与磁场平行时，出现最大值。

最大电动势Em=NB ωS 最大电流Im=rR Em +，R 两端的最大电压Um=I m ·R 。

B 、瞬时值:交流全路中，其电动势、电流、电压、均随时间发生周期性变化，如从中性面开始计时，其瞬时值分别为：e=Emsin ωt i=Imsin ωt u=Umsin ωtC 、有效值：对于正弦（或余弦）交流电，有效值=2最大值。

即 E=2EmI=2ImU=2UmD 、 平均值： 对于某一段时间或某一过程，其平均感应电动势： I t NE 平均电流→∆∆∙=φ=U rR E 平均电压→+=I R ∙ 2、学生容易出现的错误：（1）有效值的理解：有效值=2最大值，学生容易把条件“正弦或余弦”交流电忽视，对于非正弦或余弦交流电，学生很难建立起电流热效应方程，以求解有效值。

如：求以下交流电的有效值。

学生容易出现以下几种答案： a : U=25, b : U=23c: U=28正确的解法： 建立电流热效应方程： 2.01.031.05222⨯=⨯+⨯RU R R 即： U=17 （V ）（2）平均值的理解：如：交流发电模式中，从中性面开始，转过060，求此过程的平均电动势。

学生容易出现以下错误，把平均电动势理解为电动势的平均值，即E =S NB Em e e ω43260sin 02021=+=+ 正确的解法： E =N πωωπφ2326160cos 0S NB BS BS N t =∙-=∆∆ （3）求解功率或电热用交流电源给外电路供电，在求解功率或电热问题的时候，学生很容易把平均值与有效值混淆。