江苏省赣榆县第一中学高一数学每周一测7 Word版含答案

赣榆高级中学2020-2021学年度高一年级01月阶段检测数学试题注意事项：1.考试时间120分钟，试卷满分150分.2.答题前，考生务必将自己的姓名、准考证号填写在答题卡上.3.请用2B 铅笔和0.5毫米黑色墨水签字笔在答题卡上指定区域内作答.一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.16sin 3π⎛⎫- ⎪⎝⎭的值为（ ）A.12-B.C.122.已知α为终边上一点为(P x 且2cos 3α=-，则x 值为（ ） A.2± B.2 C.-2 D.2 3.“1sin 2x =”是“26x k ππ=+，k Z ∈”的（ ） A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件 4.已知0.6log 3a =，30.6b =，0.63c =，则（ ）A.a b c <<B.a c b <<C.c a b <<D.b c a <<5.已知幂函数()223()22()n n f x n n xn Z -=+-⋅∈在(0,)+∞上是减函数，则n 的值为（ ）A.3-B.1C.2D.1或2 6.要得到函数3sin 24y x π⎛⎫=+ ⎪⎝⎭的图象，只需将函数3sin 2y x =的图象（ ） A.向左平移4π个单位长度 B.向右平移4π个单位长度 C.向左平移8π个单位长度 D.向右平移8π个单位长度 7.函数()22sin x x y x -=-在[,]ππ-的图象大致为（ ）A. B.C. D.8.已知函数()2sin()(0)f x x ωϕω=+>满足23f π⎛⎫=⎪⎝⎭，()0f π=，且()f x 在区间5,312ππ⎛⎫ ⎪⎝⎭单调，则ω的取值个数为（ ）A.5B.6C.7D.8 二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得3分.9.下列命题为真命题的是（ ）A.若a b >，则22ac bc >B.若23a -<<，12b <<，则42a b -<-<C.若0b a <<，0m <，则m m a b> D.若a b >，c d >，则ac bd >10.“双11”购物节中，某电商对顾客实行购物优惠活动，规定一次购物付款总额满一定额度，可以给予优惠：（1）如果购物总额不超过50元，则不给予优惠；（2）如果购物总额超过50元但不超过100元，可以使用一张5元优惠券；（3）如果购物总额超过100元但不超过300元，则按标价给予9折优惠；（4）如果购物总额超过300元，其中300元内的按第（3）条给予优惠，超过300元的部分给予8折优惠. 某人购买了部分商品，则下列说法正确的是（ ）A.如果购物时一次性全部付款99元，则购物总额为104元B.如果购物总额为228元，则应付款为205.2元C.如果购物总额为368元，则应付款为294.4元D.如果购物时一次性全部付款442.8元，则购物总额为516元11.知函数()sin 23f x x π⎛⎫=- ⎪⎝⎭，则下列说法正确的是（ ） A.函数()f x 的最小正周期是2π B.函数()f x 增区间是5,()26212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦C.函数()f x 图象关于点,03π⎛⎫-⎪⎝⎭对称 D.函数图象关于直线23x π=对称 12.已知正数x 、y 、z 满足346x y z ==，则下列选项正确的是（ ） A.1122x y z +=B.32x y z ⎛+>⎝ C.346x y z >> D.22xy z >二、填空题：本题共4小题，每小题5分，共20分.13.若命题“x R ∃∈，使得2(1)10x a x +-+<”是真命题，则实数a 的取值范围是__________.14.已知函数()log ()a f x x m n =-+的图象恒过定点()3,5，则lg lg m n +的值是__________.15.已知7sin cos 13αα+=，(0,)απ∈，则2sin sin cos ααα-的值为__________. 16.函数1,02()52sin 2,06x x f x x x ππ⎧≤⎪⎪=⎨⎛⎫⎪+<< ⎪⎪⎝⎭⎩，若方程()f x a =恰有三个不同的解，记为1x ，2x ，3x ，则123x x x ++的取值范围是__________.四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.（本小题满分10分）在①函数()f x 的图象关于点,06π⎛⎫- ⎪⎝⎭对称； ②函数()f x 在,44ππ⎡⎤-⎢⎥⎣⎦上的最小值为-1；③函数()f x 的图象关于直线12x π=对称.这三个条件中任选两个补充在下面的问题中，再解答这个问题.已知函数()sin(2)f x A x ϕ=+（其中||2πϕ<，0A >），若满足条件________与_________，求函数()f x 的解析式.18.（本小题满分12分）已知集合{}0.5log (1)2A x x =->-∣，函数1()423x x g x +=-++的值域是集合B . （1）求集合A B ；（2）设集合{5}C xm x m =<<+∣，若“()x A B ∈”是“x C ∈”的充分条件，求实数m 的取值范围. 19.（本小题满分12分）2015年10月，屠呦呦获得诺贝尔生理学或医学奖，理由是她发现了青蒿素，这种药品可以有效降低疟疾患者的死亡率，她成为首获科学类诺贝尔奖的中国人.从青篙中提取的青篙素抗疟性超强，几乎达到100%，据监测：服药后每毫升血液中的含药量y （微克）与时间t （小时）之间近似满足如图所示的曲线.（1）写出第一服药后y 与t 之间的函数关系式()y f t =；（2）据进一步测定：每毫升血液中含药量不少于19微克时，治疗有效，求服药一次后治疗有效的时间是多长？20.（本小题满分12分） 已知函数()2()2x x a f x a R =+∈为定义在R 上的奇函数. （1）求实数a 的值；（2）判断函数()f x 的单调性，并证明；（3）解关于x 的不等式()2(3)10f mx f x -+-≤（其中m R ∈）.21.（本小题满分12分）已知函数1tan ()ln 1tan x f x x-=+. （1）判断函数()f x 的奇偶性，并证明；（2）若,42x ππ⎛⎫∀∈⎪⎝⎭，不等式()tan 0f x e a x +≥恒成立，试求实数a 的取值范围.（其中e 为自然对数的底数） 22.（本小题满分12分）已知函数()sin()f x A x ωϕ=+（其中0A >，0ω>，||2πϕ<）的图象与x 轴的交于A ，B 两点，A ，B 两点的最小距离为2π，且该函数的图象上的一个最高点的坐标为,212π⎛⎫ ⎪⎝⎭. （1）求函数()f x 的解析式；（2）求证：存在大于3π的正实数0x ，使得不等式|()|ln f x x >(0x 有解.（其中e 为自然对数的底数） 赣榆高级中学2020-2021学年度高一年级01月阶段检测数学试题参考答案及评分建议1.D2.C3.B4.A5.B6.C7.A8.D9.BC 10.BD 11.ABD 12.BD13.(,1)(3,)-∞-+∞ 14.1 15.204169 16.551,33ππ⎛⎫- ⎪⎝⎭17.解：若选①②，因为函数()f x 的图象关于点,06π⎛⎫- ⎪⎝⎭对称， 所以26k πϕπ⎛⎫⨯-+= ⎪⎝⎭，3k πϕπ=+，k Z ∈，又||2πϕ<， 所以3πϕ=， 因为44x ππ-≤≤，所以52636x πππ-≤+≤， 所以1sin 2123x π⎛⎫-≤+≤ ⎪⎝⎭， 所以min 1()12f x A =-=-，解得2A =，所以()2sin 23f x x π⎛⎫=+⎪⎝⎭. 若选②③， 因为函数()f x 的图象关于直线12x π=对称， 所以2122k ππϕπ⨯+=+，解得3k πϕπ=+，k Z ∈， 又||2πϕ<，所以3πϕ=， 因为44x ππ-≤≤，所以52636x πππ-≤+≤， 所以1sin 2123x π⎛⎫-≤+≤ ⎪⎝⎭， 所以min 1()12f x A =-=-， 解得2A =，所以()2sin 23f x x π⎛⎫=+ ⎪⎝⎭. 18.解：（1）集合{15}A xx =<<∣ 由()()221()4232223214x x x x x g x +=-++=-+⋅+=--+，且20x >， 故函数1()423x x g x +=-++的值域{4}B y y =≤∣，{14}A B x x =<≤∣.（2）由（1）得：{14}AB x x =<≤∣， 由题意可得()A BC ⊆，得154m m ≤⎧⎨+>⎩则实数m 的取值范围是11m -<≤19.解：（1）设,011,13t a kt t y t -≤≤⎧⎪=⎨⎛⎫> ⎪⎪⎝⎭⎩，当1t =时，由9y =得9k =，由1193a -⎛⎫= ⎪⎝⎭得3a =；∴39,011,13t t t y t -≤≤⎧⎪=⎨⎛⎫> ⎪⎪⎝⎭⎩；（2）由19y ≥得01199t t ≤≤⎧⎪⎨≥⎪⎩或311139t t ->⎧⎪⎨⎛⎫≥ ⎪⎪⎝⎭⎩； 解得1581t ≤≤； ∴服药一次后治疗有效的时间长是180548181-=小时. 20.解：（1）∵()f x 为定义在R 上奇函数，∴()()f x f x -=-恒成立， ∴2222x x x x a a --⎛⎫+=-+ ⎪⎝⎭， ∴12(1)02x x a ⎛⎫++= ⎪⎝⎭在在R 上恒成立，等价于10a +=，即1a =-； （利用()00f =得到1a =-，没有定义验证的，本问仅得1分）（2）1()22x x f x =-，任取12,x x R ∈，且12x x < ()()()1212121221121211111222222122222x x x x x x x x x x x x f x f x +⎛⎫⎛⎫-=---=-+-=-+ ⎪ ⎪⎝⎭⎝⎭ ∵12x x <∴1222x x< ∴()()12f x f x <即()f x 在R 上为单调递增函数（3）∵()f x 为奇函数∴()2(3)10f mx f x -+-≤等价于()2(3)1f mx f x -≤- ∵()f x 在R 上为单调递增函数，∴231mx x -≤-，即220x mx -+≥， 当280m ∆=-≤，即m -≤≤R当280m ∆=->，即m <-m >，不等式的解集为m m ⎛⎡⎫+-∞+∞ ⎪⎢ ⎪⎥⎢⎝⎦⎣⎭21.解（1）1tan ()ln 1tan x f x x -=+的x 满足的不等关系有：1tan 01tan x x ->+ 即(1tan )(tan 1)0x x +-<，故tan 1tan 1x x <⎧⎨>-⎩，解得44k x k ππππ-+<<+，k Z ∈，故函数的定义域为,44k k ππππ⎛⎫-++ ⎪⎝⎭，k Z ∈，该定义域关于原点对称. 又1tan 1tan ()ln ln ()1tan 1tan x x f x f x x x +--==-=--+， 故函数()f x 为奇函数.（没有求定义域的，本问仅得2分）（2）令tan t x =，因为,42x ππ⎛⎫∈ ⎪⎝⎭，故1t >. 故在,42ππ⎛⎫ ⎪⎝⎭上不等式()tan 0f x e a x +≥恒成立即为任意1t >，不等式101t at t -+≥+恒成立， 所以1(1)t a t t -≥+在(1,)+∞上恒成立， 令1s t =-，则0s >且2112(1)323t s t ts s s s-==+++++，由基本不等式有2s s+≥s =所以13(1)t t t -≤=-+1t =时等号成立， 故1(1)t y t t -=+的最大值为3-， 所以a 的取值范围为[3)-+∞.22.解：（1）由题意可知，2A =函数()f x 的周期为π，故2ω= 故()2sin(2)f x x ϕ=+，由得212f π⎛⎫= ⎪⎝⎭，3πϕ= ()2sin 23f x x π⎛⎫=+ ⎪⎝⎭（2）证明：因为03x π⎛∈ ⎝，故当(0x x ∈时，10ln 2x <<原不等式可化为|()|f x x >又因为10ln 2x <<，则12x >要使得|()|f x x >在(0x 有解，只需1|()|2f x >在区间(0x 有解代入得：sin 232x π⎛⎫+> ⎪⎝⎭当sin 232x π⎛⎫+> ⎪⎝⎭解得，即,6x k k πππ⎛⎫∈+ ⎪⎝⎭，k Z ∈时此时与区间,6k k πππ⎛⎫+ ⎪⎝⎭与区间(0x 的交集为空集当sin 23x π⎛⎫+< ⎪⎝⎭,23x k k ππππ⎛⎫∈-- ⎪⎝⎭，k Z ∈时令1k =得2,23x ππ⎛⎫∈ ⎪⎝⎭时，满足sin 23x π⎛⎫+> ⎪⎝⎭2π>，故只需0,32x ππ⎛⎫∈ ⎪⎝⎭，原不等式在区间(0x 有解。

2024年连云港市赣榆一中高一数学3月份考试卷（试卷满分150分．考试用时120分钟）2024年3月一、单选题（本题共8小题，每小题5分，共40分）1．如果用,i j 分别表示x 轴和y 轴正方向上的单位向量，且()()2,3,4,2A B ，则AB可以表示为（）A ．23i j+ B ．42i j + C ．2i j - D ．2i j-+ 2．cos1875= （）A ．4B ．4C ．4D ．43．已知向量(),3a m = ，()1,b m = ，若a 与b方向相反，则a = （）A ．54B ．48C ．D ．4．我国古代数学家僧一行应用“九服晷影算法”在《大衍历》中建立了晷影长1与太阳天顶距()0180θθ︒≤≤︒的对应数表，这是世界数学史上较早的一张正切函数表，根据三角学知识可知，晷影长度l 等于表高h 与太阳天顶距θ正切值的乘积，即tan l h θ=．对同一“表高”两次测量，第一次和第二次太阳天顶距分别为,αβ，且1tan()3αβ-=，若第二次的“晷影长”与“表高”相等，则第一次的“晷影长”是“表高”的（）A ．1倍B ．2倍C ．3倍D ．4倍5．如图所示的矩形ABCD 中，E ，F 满足BE EC =，2CFFD =，G 为EF 的中点，若AG AB AD λμ=+ ，则λμ的值为（）A ．12B ．3C ．34D ．26．若方程e 1xm -=有两个不同的实数根，则实数m 的取值范围为（）A ．()0,∞+B ．(]0,1C ．()0,1D ．()1,+∞7．若π02α<<，02βπ<<，3cos()5αβ+=，π5sin 413β⎛⎫-= ⎪⎝⎭，则πcos 4α⎛⎫+= ⎪⎝⎭（）A ．22B ．32C ．5665D ．36658．已知a ，b是单位向量，0a b ⋅= ，若向量c 满足341c b a --= ，则c r 的取值范围为（）A ．1⎤⎦B ．1⎡⎤⎣⎦C ．[]5,6D ．[]4,6二、多选题（本题共4小题，毎小题5分，共20分.全选对的得5分，部分选对的得2分，选错不得分）9．下列说法正确的是（）A ．向量a 在向量b上的投影向量可表示为a b b bb⋅⋅B ．若0a b ⋅< ，则a 与b 的夹角θ的范围是π,π2⎛⎤ ⎥⎝⎦C ．若ABC 是等边三角形，则AB，BC 的夹角为60︒D ．若0a b ⋅= ，则a b⊥ 10．已知ABC 中，内角A B C ，，所对的边分别为a b c ，，，且301A a c === ，，则b 的值可能是（）A ．1B CD ．211．下列等式正确的是（）A ．1sin15cos154︒︒=B ．22sin 22.512︒-=C ．sin26cos34cos26sin342︒︒+︒︒=D ．tan 71tan 2611tan 71tan 26︒-=+︒︒︒12．在平面四边形ABCD 中，1AB BC CD DA DC ===⋅= ，12BA BC ⋅= ，则（）A ．1AC =B ．CA CD⊥ C ．AD = D ．22BD =三、填空题（本题共4题，每小题5分，共20分）13．已知向量,a b 满足1,2a b a b ==-= a 与b的夹角为.14．已知函数()2xf x x =+的零点在区间(),1n n +内，Z n ∈，则n =．151cos80=.16．在ABC 中，2cos ,4,33C AC BC ===，则sin A =.四、解答题17．已知平面向量(,1),(,23),R a m b m m m ==-+∈．(1)若1,(1,23)m c ==- ，求满足c a b λμ=+的λ和μ的值；(2)若a b ⊥，求m 的值．18．在ABC 中，4AB =，AC =213cos 13BAC ∠=-，D 为线段BC 的中点.(1)求BC 的长；(2)求cos ADC ∠的值.19．如图所示，在ABC 中，D 为BC 边上一点，且2BD DC =．过D 点的直线EF 与直线AB 相交于E点，与直线AC 相交于F 点（E ，F 两点不重合）．(1)用AB，AC 表示AD ；(2)若AE AB λ= ，AF AC μ= ，求12λμ+的值．20．（1）设π02βα<<<，且113cos ,cos(),714ααβ=-=求角β的值；（2）已知2tan 3α=，且3sin(2)sin 2αββ+=，求tan()αβ+的值．21．已知()3,4OA =- ，()6,3OB =- ，()5,3OC m m =---．(1)若点A 、B 、C 不能构成三角形，求m 的值；(2)若点A 、B 、C 构成的三角形为直角三角形，求m 的值．22．已知向量()([]cos ,sin ,3,,0,πa x x b x ==∈.(1)若()a b b +∥，求x 的值；(2)记()f x a b =⋅ ，求函数()f x 的图象向右平移π3个单位，纵坐标不变横坐标变为原来的2倍，得到函数()g x 的图象，求函数()g x 的值域.1．C【分析】先根据向量的坐标表示求出AB，再根据正交分解即可得解.【详解】因为()()2,3,4,2A B ，所以()2,1AB =-，所以2AB i j =- .故选：C.2．C【分析】根据诱导公式将cos1875︒化简，再由余弦的和差角公式即可得到结果.【详解】因为()cos1875cos 360575cos 75=︒⨯+︒=︒，则()cos75cos 3045cos30cos45sin 30sin 45︒=︒+︒=︒︒-︒︒1122224=-故选:C 3．D【分析】首先根据题意得到m =，再求a即可.【详解】向量(),3a m = ，()1,b m = ，若a 与b方向相反，所以230m -=，解得m =所以())()3a -=--=-，a == .故选：D 4．B【分析】根据给定条件，可得tan 1β=，再利用和角的正切公式计算作答.【详解】依题意，tan 1β=，则11tan()tan 3tan tan[()]211tan()tan 13αββααββαββ+-+=-+===--⋅-，所以第一次的“晷影长”是“表高”的2倍.故选：B 5．A【分析】以,AB AD为基底，根据平面向量线性运算即可求解.【详解】因为BE EC =，2CF FD = ，G 为EF 的中点，所以()()11112222AG AE AF AB BE AD DF =+=+++1111111122232223AB BC AD DC AB AD AD AB ⎛⎫⎛⎫⎛⎫⎛⎫=+++=+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭2334AB AD =+，所以23,34λμ==，所以231342λμ=⨯=.故选：A6．C【分析】把方程根的问题转化为两个函数图象交点的问题，画出函数图象，利用数形结合的思想即可求解．【详解】令()e 1xf x =-，由于当0x <时，1e 10x -<-<，()1e xf x ∴=-，且()()0,1f x ∈；当0x ≥时，e 10x -≥，()e 1xf x ∴=-，且()[)0,f x ∈+∞，作出函数()f x的图象如图所示，则当01m <<时，函数()e 1x f x =-与y m =的图象有两个交点，即方程e 1xm -=有两个不同的实数根，m ∴的取值范围是()0,1．故选：C ．【分析】由已知，结合角的范围，即可得出4sin()5αβ+=，π12cos 413β⎛⎫-= ⎪⎝⎭.然后根据两角差余弦公式，即可得出答案.【详解】因为π02α<<，02βπ<<，所以0παβ<+<，所以，4sin()5αβ+==.又πππ444β-<-<，所以π12cos 413β⎛⎫-== ⎪⎝⎭.所以，()ππcos cos 44ααββ⎡⎤⎛⎫⎛⎫+=+-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦()()ππcos cos sin sin 44αββαββ⎛⎫⎛⎫=+-++- ⎪ ⎪⎝⎭⎝⎭312455651351365=⨯+⨯=.故选：C.8．D【分析】将341c b a --= 两边同时平方，转化为关于c r的一元二次不等式即可求解.【详解】∵,a b是单位向量，∴1a b == .∵341c b a --= ∴()222234234924161c b a c c b a b a b a --=-⋅+++⋅+= 且0a b ⋅= .∴()223424c b a c ⋅+=+ ，又∵345b a +=，∴22425cos c c θ+=⨯⨯ (θ是c 与34b a +的夹角)．又－1≤cos θ≤1，∴2242410c c ≤+≤，∴210240c c -+≤.根据一元二次不等式的解法，解得46c ≤≤.故选：D.【分析】根据投影向量的定义即可判断A ；根据数量积的计算公式即可判断B ；根据向量夹角的定义即可判断C ，根据数量积的计算公式即可判断D.【详解】对于选项A ，根据投影向量的定义可得向量a 在向量b上的投影向量为a b bb b⋅⋅，故A 正确；对于选项B ，因为cos 0a b a b θ⋅=< ，所以cos 0θ<，又0πθ≤≤，所以π,π2θ⎛⎤∈ ⎥⎝⎦，故B 正确；对于选项C ，若ABC 是等边三角形，则AB，BC 的夹角为120︒，故C 错误；对于选项D ，因为0a b ⋅= ，所以a b ⊥ 或0a =或0b = ，故D 错误．故选：AB.10．AD【分析】根据给定条件，利用余弦定理求解判断作答.【详解】在ABC 中，30,1,A a c === 2222cos a b c bc A =+-得：231322b b =+-，即2320b b -+=，解得1b =或2b =，所以b 的值可能是1或2.故选：AD 11．ACD【分析】利用二倍角公式和两角和差公式求解即可.【详解】11sin15cos15sin 3024︒︒=︒=，A 正确；222sin 22.51cos 452︒-=-︒=-，B 错误；()3sin 26cos34cos 26sin 34sin 2634sin 602︒︒+︒︒=︒+︒=︒=，C 正确；()tan 71tan 26tan 7126tan 4511tan 71tan 26︒-︒=︒-︒=︒=+︒︒，D 正确；故选：ACD 12．ABD【分析】根据数量积的定义求出ABC ∠，即可得到ABC 为等边三角形，从而判断A ，设AD x =，在ACD 中，由余弦定理及数量积的定义求出x ，即可得到=90ACD ∠︒，从而判断B ，根据150BCD ∠=︒，=45ADC ∠︒，知AD 与BC 不平行，即可判断C ，最后由余弦定理判断D.【详解】解：选项A ，由1AB BC == ，1cos 2BA BC BA BC ABC ⋅=⋅∠= ，所以1cos 2ABC ∠=，又0180ABC ︒<∠<︒，所以60ABC ∠=︒，所以ABC 为等边三角形，所以1AC =，故A 正确；选项B ，设AD x =，在ACD 中，由余弦定理知，2222cos AC AD CD AD CD ADC =+-⋅∠，即21121cos x x ADC =+-⋅⋅∠，所以cos 2xADC ∠=，由1cos 12xDA DC DA DC ADC x ⋅==⋅∠=⋅⋅，解得x =x =所以222AD AC CD =+，即ACD 为等腰直角三角形且=90ACD ∠︒，所以CA CD ⊥，故B 正确；对于C ，因为6090150BCD ACB ACD ∠=∠+∠=︒+︒=︒，=45ADC ∠︒，所以AD 与BC 不平行，故C 错误；选项D ，在BCD △中，由余弦定理知2222cos BD BC CD BC CD BCD =+-⋅∠，22112112⎛=+-⨯⨯⨯= ⎝⎭所以222BD BD == D 正确．故选：ABD ．13．π4【分析】根据向量数量积公式，求得a b ⋅的值，再根据夹角公式，即可求解.【详解】因为1,2a b a b ==-= 所以()222222|2|2444||||42a b a b a b a b a b a b -=-=+-⋅=+-⋅=，所以1a b ⋅=，所以cos ,2a b a b a b ⋅==，又因为[],0,πa b ∈ ，所以π,4a b = .故答案为：π414．1-【分析】利用零点存在定理可得答案.【详解】明显函数()2xf x x =+在R 上单调递增，且为连续函数，又()010f =>，()1021112f --+=--=<，由零点存在定理得函数()2xf x x =+的零点在区间()1,0-内，故1n =-.故答案为：1-.15．4-【分析】先用诱导公式转化cos8010sin = ，再对已知分式进行通分，分子化成一个三角函数，再使用二倍角公式即可得到结果.【详解】()sin sin sin sin 210301110cos1022041cos10cos80cos101010cos1010cos1sin s 22in 00---=-==--= .故答案为：4-.16【分析】由已知在ABC 中利用余弦定理可得AB 的值，可求AB BC =，可得A C =，即可得解sin A 的值．【详解】因为在ABC 中，2cos 3C =，4AC =，3BC =，由余弦定理得3AB ==，所以AB BC =，即A C =，则2cos cos 3A C ==，又由22sin cos 1A A +=,所以sin 3A =．17．(1)34λμ=⎧⎨=⎩(2)1m =-或3m =【分析】（1）利用向量相等列出关于λ和μ的方程组，解之即可求得λ和μ的值；（2）利用向量垂直充要条件列出关于m 的方程，解之即可求得m 的值．【详解】（1）当1m =时，(1,1),(1,5)a b ==-∴(,)(,5)(,5)(1,23)a b λμλλμμλμλμ+=+-=-+=-∴1523λμλμ-=-⎧⎨+=⎩，解之得34λμ=⎧⎨=⎩（2）由a b ⊥ ，可得=0a b ⋅，又(,1),(,23),R a m b m m m ==-+∈，则2230m m -++=解得：1m =-或3m =18．(1)10BC =(2)3cos 5ADC ∠=-【分析】（1）（2）由余弦定理求解，【详解】（1）由余弦定理得2222cos BC AB AC AB AC BAC =+-⋅⋅∠，即2165232100BC =++=，得10BC =，（2）由题意得5BD CD ==，在ACD 中，由余弦定理得222227cos 210AD CD AC AD ADC AD CD AD +--∠==⋅，在ABD △中，由余弦定理得22229cos 210AD BD AB AD ADB AD BD AD+-+∠==⋅，而ADC ADB π∠+∠=，故2227(9)AD AD -=-+，得3AD =，故3cos 5ADC ∠=-19．(1)1233AD AB AC =+(2)3.【分析】（1）向量的线性表示，利用三角形法则及题所给条件即可；（2）根据（1）的结论，转化用AE ，AF 表示AD，根据,,D E F 三点共线找出等量关系；【详解】（1）在ABD △中，由AD AB BD =+,又2BD DC = ，所以23BD BC = ，所以23AD AB BD AB BC=+=+ ()23AC ABAB =+- 2233AB ACAB =-+ 1233AB AC =+（2）因为1233AD AB AC =+ ，又AE AB λ= ，AF ACμ= 所以1AB AE λ= ，1AC AF μ= ，所以3231A E D A A F μλ=+ ，又,,D E F 三点共线，且A 在线外，所以有：12133λμ+=，即123λμ+=.20．（1）π3β=；（2）103【分析】(1)利用同角三角函数的基本关系和余弦的两角差公式求解；(2)利用正弦的两角和、差公式化简证明即可.【详解】（1）π02βα<<<，且113cos ,cos(),714ααβ=-=sin 7α∴=，sin()14αβ-=，[]1cos cos ()cos cos()sin sin()2βααβααβααβ=--=-+-=，又因为π02βα<<<，所以π3β=，()2由3sin(2)sin 2αββ+=得[][]3sin ()sin ()2ααβαβα++=+-，则2sin cos()2cos sin()3sin()cos 3cos()sin a αβααβαβααβα+++=+-+，即有10tan()5tan 3αβα+==．21．(1)12m =(2)74m =或34m =-或12m =【分析】（1）点A 、B 、C 不能构成三角形说明三点共线，利用共线性质列出方程解出参数即可；（2）分类讨论直角的情况，转化为向量数量积为0，列出方程解出即可.【详解】（1）因为点A 、B 、C 不能构成三角形，所以点A 、B 、C 三点共线，所以AB ∥AC ，因为()3,1AB OB OA =-= ，()2,1AC OC OA m m =-=-- ，所以()()3112m m ⨯-=⨯-，即12m =，所以若点A 、B 、C 不能构成三角形，则12m =.（2）若点A 、B 、C 构成的三角形为直角三角形，则：①若A 为直角，此时AB AC AB AC ⊥⇒⊥ ，即03(2)1(1)0AB AC m m ⋅=⇒⨯-+⨯-= ，所以74m =，②若B 为直角，此时AB BC AB BC ⊥⇒⊥ ，即0AB BC ⋅= ，由()1,BC OC OB m m =-=--- 所以3(1)1()0m m ⨯--+⨯-=所以34m =-，③若A 为直角，此时BC AC BC AC ⊥⇒⊥ ，即()()01(2)(1)0BC AC m m m m ⋅=⇒--⨯-+-⨯-= ，解得m =所以若点A 、B 、C 构成的三角形为直角三角形，则74m =或34m =-或m =.22．(1)56π(2)【分析】（1）利用向量坐标的线性运算得a b + 的坐标，根据()a b b +∥ 的坐标关系可得sin x x =，从而可得3tan 3x =，[0,π]x ∈，即可求解x 的值；（2）求解()f x a b =⋅ 化成余弦型函数，再由三角函数图象变化得()g x ，根据余弦函数图象性质求函数()g x 的值域即可.【详解】（1）解：()(cos ,sin ,3,a x x b == ，(cos 3,sin a b x x ∴+=+ ()a b b + ，()((cos 3sin 30x x ∴+⋅-⋅=sin x x ∴=，即tan x =[0,π]x ∈ ，5π6x ∴=.（2）解：()π3cos 6f x a b x x x ⎛⎫=⋅=-=+ ⎪⎝⎭由()f x 图象向右平移π3，横坐标变为2倍得()1π26g x x ⎛⎫=- ⎪⎝⎭[]0,πx ∈ ，1πππ,2663x ⎡⎤∴-∈-⎢⎥⎣⎦cos y x = 在π,06⎡⎤-⎢⎥⎣⎦单调递增，π0,3⎡⎤⎢⎥⎣⎦单调递减1π1cos ,1262x ⎛⎫⎡⎤∴-∈ ⎪⎢⎥⎝⎭⎣⎦1π26x ⎛⎫∴-∈ ⎪⎝⎭，即()g x 值域为.。

2023-2024学年江苏省连云港市赣榆区高一（上）期中数学试卷一、单项选择题（本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合A ＝{1，2，3}，B ＝{1，3，4}，则A ∩B ＝（ ） A ．{1}B ．{1，3}C ．{1，3，4}D ．{1，2，4}2．命题“∀x ＞0，x 2+x +1＞0”的否定是（ ） A ．∃x ≤0，x 2+x +1＜0 B ．∃x ＞0，x 2+x +1＞0C ．∃x ≤0，x 2+x +1≤0D ．∃x ＞0，x 2+x +1≤03．“x ＞1”是“x 2＞1”的（ ） A ．必要不充分条件 B ．充分不必要条件 C ．充要条件D ．既不充分也不必要条件 4．已知函数f （x +1）＝x 2，则f （2）的值为（ ） A ．1B ．2C ．3D ．45．已知函数f （x ）＝x 2﹣2mx +1在（﹣∞，1）上单调递减，则实数m 的取值范围是（ ） A ．（﹣∞，﹣1）B ．[﹣1，+∞）C ．（﹣∞，1）D ．[1，+∞）6．函数f(x)={x 2+2x −1，−3≤x ≤0，x −1，0＜x ≤5，的值域是（ ）A ．[﹣1，3]B ．[﹣1，4]C ．[﹣2，4]D ．[﹣2，2]7．下棋可以锻炼脑部，促进脑细胞新陈代谢，锻炼脑力发育，开发智力．围棋拥有19×19的超大棋盘，成为状态空间复杂度最高的棋类运动，其状态空间复杂度上限M 约为3361，而中国象棋的状态空间复杂度上限N 为1048，则下列各数中与MN 最接近的是（ ）（lg 3≈0.48）A ．10105B ．10125C ．10145D ．101658．已知对任意两个实数m ，n ，定义max{m ，n}={m ，m ≥n ，n ，m ＜n ，设函数f （x ）＝|x |﹣1，g （x ）＝x 2﹣2ax +a +1，设函数h （x ）＝max {f （x ），g （x ）}，若存在x 使得h （x ）≤0成立，则实数a 的取值范围为（ ） A ．(−∞，1−√52]∪(1+√52，+∞) B ．(−∞，−1]∪(1+√52，+∞)C ．（﹣∞，﹣1]∪[2，+∞）D ．(−∞，1−√52]∪[2，+∞) 二、多项选择题（本大题共4个小题，每小题5分，共20分，在每小题给出的选项中，有多项是符合题目要求的.全选对的得5分，部分选对的得2分，有选错的得0分） 9．已知a ，b ，c ∈R 且b ＞a ＞0，则下列结论正确的是（ ） A ．a 2＜b 2B ．ab ＜b 2C ．1a＜1bD ．ac 2＜bc 210．设集合A ＝{x |x 2﹣5x +6＝0}，B ＝{x |ax ﹣1＝0}，若A ∩B ＝B ，则实数a 的值可以为（ ） A ．12B ．0C ．3D ．1311．“若f （x ）＞f （0）对任意的x ∈（0，2]都成立，则f （x ）在[0，2]上是增函数”为假命题，则下列函数中符合上述条件的是（ ） A ．y ＝﹣x 2+3xB ．y ＝x 2+x +1C ．y =x +1x+1D ．y ={1x，1＜x ≤2x ，0＜x ≤112．已知函数y ＝f （x ），x ∈R ，且对任意的x ，y ∈R ，f （x +y ）＝f （x ）+f （y ）﹣1，当x ＞0时，f （x ）＞1，且f （1）＝2，则下列说法正确的是（ ） A ．f （0）＝1B ．f （﹣1）＝1C ．f （x ）在R 上是减函数D ．f （x ）在[﹣3，3]上的最小值为﹣2三、填空题（本大题共4个小题，每小题5分，共20分）13．已知U ＝R ，A ＝（﹣1，3]，B ＝[2，+∞），则A ∩（∁U B ）＝ ． 14．函数y =1x−1的单调递减区间是 ． 15．若不等式|x ﹣2|＜a 的一个必要条件为﹣2＜x ≤1，则实数a 的取值范围是 ．16．设函数f （x ）的定义域为R ，满足f （x +1）＝3f （x ），且当x ∈（0，1]时，f （x ）＝﹣x 2+2x ．若对任意x ∈（﹣∞，m ]，都有f(x)≤32，则实数m 的取值范围是 ．四、解答题（本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．（10分）计算下列各式的值． （1）π0−[(−2)2]12+(278)23； （2）2lg 5+lg 4﹣e ln 2﹣log 34×log 43．18．（12分）已知函数f(x)=|−x 2+2x|，x ∈[0，73]． （1）画出函数f （x ）的图象，并写出单调区间； （2）求函数f （x ）的值域．19．（12分）已知命题p ：关于x 的方程x 2﹣mx +m 2﹣2m +1＝0有实数根，命题q ：1﹣2a ＜m ＜a +1． （1）若命题p 是真命题，求实数m 的取值范围；（2）若q是p的充分条件，求实数a的取值范围．，x∈(1，+∞)．20．（12分）已知函数f(x)=xx−1（1）判断函数f（x）在（1，+∞）上的单调性，并利用定义证明；（2）若f（2a+1）＞f（a+2），求实数a的取值范围．21．（12分）设矩形ABCD（AB＜AD）的周长为36cm，把△ACD沿AC向△ABC折叠，AD折过去后交BC于点P．当矩形ABCD的边长为多少时，△ABP的面积最大？并求出这个最大值．22．（12分）设函数f（x）＝x2﹣tx+1，其中t＞0．（1）若t＝1，解关于x的不等式mf（x）＞x+m﹣1（m＞0）；（2）当x∈[﹣1，3]时，f（x）的最大值记为M（t），最小值记为L（t），求g（t）＝M（t）﹣L（t）的解析式．2023-2024学年江苏省连云港市赣榆区高一（上）期中数学试卷参考答案与试题解析一、单项选择题（本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合A＝{1，2，3}，B＝{1，3，4}，则A∩B＝（）A．{1}B．{1，3}C．{1，3，4}D．{1，2，4}解：因为集合A＝{1，2，3}，B＝{1，3，4}，所以A∩B＝{1，3}．故选：B．2．命题“∀x＞0，x2+x+1＞0”的否定是（）A．∃x≤0，x2+x+1＜0B．∃x＞0，x2+x+1＞0C．∃x≤0，x2+x+1≤0D．∃x＞0，x2+x+1≤0解：根据题意，命题“∀x＞0，x2+x+1＞0”是全称量词命题，其否定为：∃x＞0，x2+x+1≤0．故选：D．3．“x＞1”是“x2＞1”的（）A．必要不充分条件B．充分不必要条件C．充要条件D．既不充分也不必要条件解：因为{x|x2＞1}＝{x|x＞1或x＜﹣1}，所以“x＞1”是“x2＞1”充分不必要条件．故选：B．4．已知函数f（x+1）＝x2，则f（2）的值为（）A ．1B ．2C ．3D ．4解：f （x +1）＝x 2，令x +1＝2，解得x ＝1，故f （2）＝1． 故选：A ．5．已知函数f （x ）＝x 2﹣2mx +1在（﹣∞，1）上单调递减，则实数m 的取值范围是（ ） A ．（﹣∞，﹣1）B ．[﹣1，+∞）C ．（﹣∞，1）D ．[1，+∞）解：因为f （x ）＝x 2﹣2mx +1在（﹣∞，1）上单调递减，所以m ≥1． 故选：D ．6．函数f(x)={x 2+2x −1，−3≤x ≤0，x −1，0＜x ≤5，的值域是（ ）A ．[﹣1，3]B ．[﹣1，4]C ．[﹣2，4]D ．[﹣2，2]解：当﹣3≤x ≤0时，y ＝x 2+2x ﹣1＝（x +1）2﹣2，根据二次函数的性质可知，当x ＝﹣1时，函数取得最小值﹣2， 当x ＝﹣3时，函数取得最大值2，即﹣2≤y ≤2， 当0＜x ≤5时，y ＝x ﹣1∈（﹣1，4]，故﹣2≤y ≤4． 故选：C ．7．下棋可以锻炼脑部，促进脑细胞新陈代谢，锻炼脑力发育，开发智力．围棋拥有19×19的超大棋盘，成为状态空间复杂度最高的棋类运动，其状态空间复杂度上限M 约为3361，而中国象棋的状态空间复杂度上限N 为1048，则下列各数中与MN最接近的是（ ）（lg 3≈0.48）A ．10105B ．10125C ．10145D ．10165解：由题意可知，M ≈3361，N ≈1048，则lgM ≈361lg 3，lgN ≈48， 故lgMN =lgM ﹣lgN ≈361×0.48﹣48≈125，故M N≈10125． 故选：B ．8．已知对任意两个实数m ，n ，定义max{m ，n}={m ，m ≥n ，n ，m ＜n ，设函数f （x ）＝|x |﹣1，g （x ）＝x 2﹣2ax +a +1，设函数h （x ）＝max {f （x ），g （x ）}，若存在x 使得h （x ）≤0成立，则实数a 的取值范围为（ ） A ．(−∞，1−√52]∪(1+√52，+∞) B ．(−∞，−1]∪(1+√52，+∞)C ．（﹣∞，﹣1]∪[2，+∞）D ．(−∞，1−√52]∪[2，+∞) 解：f （x ）＝|x |﹣1，g （x ）＝x 2﹣2ax +a +1，则f （x ）的函数图象如下图所示．g （x ）＝x 2﹣2ax +a +1是二次函数，开口向上，对称轴方程为x ＝a ， 因为当|x |＞1时，f （x ）＞0，所以h （x ）＝max {f （x ），g （x ）}＞0恒成立， 所以只需要考虑x ∈[﹣1，1]，此时f （x ）≤0．（1）当a ≤﹣1时，g （x ）＝x 2﹣2ax +a +1在[﹣1，1]上单调递增，若存在x 使得h （x ）≤0成立，需要g （x ）min ≤0，即g （﹣1）＝（﹣1）2﹣2a （﹣1）+a +1＝3a +2≤0，即a ≤−23， 则存在x 使得h （x ）≤0成立，故a ≤﹣1；（2）当﹣1＜a ＜1时，g （x ）＝x 2﹣2ax +a +1在[﹣1，1]上先单调递减后单调递增，需要g(x)min =g(a)=a 2−2a ⋅a +a +1=−a 2+a +1≤0， 即a 2﹣a ﹣1≥0，解得a ≥1+√52或a ≤1−√52， 又1+√52＞1，0＞1−√52＞−1，所以−1＜a ≤1−√52； （3）当a ≥1时，g （x ）＝x 2﹣2ax +a +1在[﹣1，1]上单调递减，需要g （1）＝12﹣2a +a +1＝﹣a +2≤0，即a ≥2， 综上，a 的取值范围为(−∞，1−√52]∪[2，+∞)． 故选：D ．二、多项选择题（本大题共4个小题，每小题5分，共20分，在每小题给出的选项中，有多项是符合题目要求的.全选对的得5分，部分选对的得2分，有选错的得0分） 9．已知a ，b ，c ∈R 且b ＞a ＞0，则下列结论正确的是（ ） A ．a 2＜b 2B ．ab ＜b 2C ．1a＜1bD ．ac 2＜bc 2解：已知a ，b ，c ∈R 且b ＞a ＞0，不妨设b ＝2，a ＝1，c ＝0， 检验可得，C 、D 都不成立，只有A 、B 成立， 故选：AB ．10．设集合A ＝{x |x 2﹣5x +6＝0}，B ＝{x |ax ﹣1＝0}，若A ∩B ＝B ，则实数a 的值可以为（ ） A ．12B ．0C ．3D ．13解：A ＝{x |x 2﹣5x +6＝0}＝{2，3}， A ∩B ＝B ，则B ⊆A ，当a ＝0时，B ＝∅，符合题意， 当a ≠0时，B ＝{1a }，则1a=2或1a=3，解得a =12或a =13．故选：ABD ．11．“若f （x ）＞f （0）对任意的x ∈（0，2]都成立，则f （x ）在[0，2]上是增函数”为假命题，则下列函数中符合上述条件的是（ ） A ．y ＝﹣x 2+3xB ．y ＝x 2+x +1C ．y =x +1x+1D ．y ={1x，1＜x ≤2x ，0＜x ≤1解：根据二次函数的性质可知，y ＝﹣x 2+3x 在（0，32]上单调递增，在（32，2]上单调递减，故f （x ）＞f （0），但f （x ）在[0，2]上不单调，A 符合题意； y ＝x 2+x +1在[0，2]上单调递增，B 不符合题意； 令t ＝x +1，由0＜x ≤2可得1＜t ≤3，则y ＝x +1x+1=x +1+1x+1−1＝t +1t −1在[1，3]上单调递增，不符合题意；当1＜x ＜2时，y =1x单调递减，当0＜x ≤1时，y ＝x 单调递增，但函数y ={1x ，1＜x ≤2x ，0＜x ≤1在[，2]上不单调，符合题意．故选：AD ．12．已知函数y ＝f （x ），x ∈R ，且对任意的x ，y ∈R ，f （x +y ）＝f （x ）+f （y ）﹣1，当x ＞0时，f （x ）＞1，且f （1）＝2，则下列说法正确的是（ ） A ．f （0）＝1B ．f （﹣1）＝1C ．f （x ）在R 上是减函数D ．f （x ）在[﹣3，3]上的最小值为﹣2解：f （x +y ）＝f （x ）+f （y ）﹣1，令x ＝y ＝0，则f （0）＝2f （0）﹣1，解得f （0）＝1，故A 正确； 令x ＝1，y ＝﹣1，则f （0）＝f （1）+f （﹣1）﹣1，因为f （1）＝2，解得f （﹣1）＝0，故B 错误； 令x ＝x 1，y ＝x 2﹣x 1，且x 1＜x 2，则f （x 1+x 2﹣x 1）＝f （x 1）+f （x 2﹣x 1）﹣1，即f （x 2）﹣f （x 1）＝f （x 2﹣x 1）﹣1，因为当x ＞0时，f （x ）＞1，故f （x 2﹣x 1）＞1， 所以f （x 2）﹣f （x 1）＝f （x 2﹣x 1）﹣1＞0，故f （x 2）＞f （x 1）， 所以f （x ） 在R 上是增函数，故C 错误；令x ＝y ＝﹣1，则f （﹣2）＝f （﹣1）+f （﹣1）﹣1＝﹣1， 令x ＝﹣1，y ＝﹣2得f （﹣3）＝f （﹣1）+f （﹣2）﹣1＝﹣2， 由于f （x ）在R 上是增函数，故f （x ）在[﹣3，3]单调递增， 故最小值为f （﹣3）＝﹣2，故D 正确． 故选：AD ．三、填空题（本大题共4个小题，每小题5分，共20分）13．已知U ＝R ，A ＝（﹣1，3]，B ＝[2，+∞），则A ∩（∁U B ）＝ ． 解：因为U ＝R ，A ＝（﹣1，3]，B ＝[2，+∞）， 所以∁U B ＝（﹣∞，2）， 所以A ∩（∁U B ）＝（﹣1，2）． 故答案为：（﹣1，2）．14．函数y =1x−1的单调递减区间是 ． 解：根据反比例函数的性质及函数图象的平移可知， y =1x−1的单调递减区间是 （1，+∞），（﹣∞，1）． 故答案为：（1，+∞），（﹣∞，1）．15．若不等式|x ﹣2|＜a 的一个必要条件为﹣2＜x ≤1，则实数a 的取值范围是 ．解：根据题意，不等式|x ﹣2|＜a 的解集包含于（﹣2，1]． 当a ≤0时，不等式|x ﹣2|＜a 的解集为空集，满足题意； 当a ＞0时，不等式|x ﹣2|＜a 即2﹣a ＜x ＜2+a ，（2﹣a ，2+a ）⊂（﹣2，1]，所以{2−a ≥−22+a ≤1，找不到符合条件的a ．综上所述，故a ≤0，即实数a 的取值范围是（﹣∞，0]． 故答案为：（﹣∞，0]．16．设函数f （x ）的定义域为R ，满足f （x +1）＝3f （x ），且当x ∈（0，1]时，f （x ）＝﹣x 2+2x ．若对任意x ∈（﹣∞，m ]，都有f(x)≤32，则实数m 的取值范围是 ． 解：f （x ）＝﹣x 2+2x 的对称轴为x ＝1，所以当x ∈（0，1]时，f （x ）函数单调递增，所以f （x ）≤f （1）＝1， 又f （x +1）＝3f （x ），所以当x ≤1时，都有f （x ）≤1， 因为当x ∈（0，1]时，f （x +1）＝3（﹣x 2+2x ），所以当x ∈（1，2]时，f （x ）＝3[﹣（x ﹣1）2+2（x ﹣1）]＝﹣3x 2+12x ﹣9， 其对称轴为x ＝2，所以f （x ）在（1，2]单调递增，令f(x)=−3x 2+12x −9=32，得x =4−√22或x =4+√22（舍去） 所以由f(x)≤32，得1＜x ≤4+√22， 综上，对任意x ∈(−∞，4−√22]都有f(x)≤32， 故实数m 的取值范围是(−∞，4−√22]． 故答案为：(−∞，4−√22]． 四、解答题（本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．（10分）计算下列各式的值． （1）π0−[(−2)2]12+(278)23； （2）2lg 5+lg 4﹣e ln 2﹣log 34×log 43．解：（1）π0−[(−2)2]12+(278)23=1−412+(32)2=1−2+94=54；（2）2lg 5+lg 4﹣e ln 2﹣log 34×log 43=lg25+lg4−2−log 34⋅1log 34=lg100−2−1=−1． 18．（12分）已知函数f(x)=|−x 2+2x|，x ∈[0，73]． （1）画出函数f （x ）的图象，并写出单调区间； （2）求函数f （x ）的值域．解：（1）根据题意，函数f(x)=|−x 2+2x|，x ∈[0，73]． 其图象如图：由图可得：f （x ）的增区间为（0，1）和(2，73)，减区间为（1，2）； （2）由（1）知当x ∈[0，1]时，函数f （x ）单调递增， 当x ∈（1，2]时，函数f （x ）单调递减，所以f （x ）在区间[0，2]上的最小值为f （0）＝0，最大值为f （1）＝1， 当x ∈(2，73]时，函数f （x ）单调递增，所以f(x)≤f(73)=79， 又因为f(1)＞f(73)，综上，f （x ）的值域为[0，1]．19．（12分）已知命题p ：关于x 的方程x 2﹣mx +m 2﹣2m +1＝0有实数根，命题q ：1﹣2a ＜m ＜a +1． （1）若命题p 是真命题，求实数m 的取值范围； （2）若q 是p 的充分条件，求实数a 的取值范围． 解：（1）若命题p 是真命题，则Δ≥0，即3m 2﹣8m +4≤0，解得：23≤m ≤2，故m 的取值范围为[23，2]；（2）设A ={x|23≤x ≤2}，B ={x|1−2a ＜x ＜a +1}，∵q 是p 的充分条件，∴B ⊆A ，当B ＝∅时，则有1﹣2a ≥a +1，解得：a ≤0，即a 的取值范围是（﹣∞，0]； 当B ≠∅时，则有{ a +1≤2，1−2a ≥23，1−2a ＜a +1，，即{a ≤1，a ≤16a ＞0，，解得：0＜a ≤16，综上，实数a 的取值范围为(−∞，16]． 20．（12分）已知函数f(x)=xx−1，x ∈(1，+∞)． （1）判断函数f （x ）在（1，+∞）上的单调性，并利用定义证明； （2）若f （2a +1）＞f （a +2），求实数a 的取值范围． 解：（1）f （x ）在区间（1，+∞）上是单调递减函数．证明：设1＜x 1＜x 2，f(x 1)−f(x 2)=x 1x 1−1−x 2x 2−1=x 2−x1(x 1−1)(x 2−1)，因为1＜x 1＜x 2，所以x 1﹣x 2＜0，x 1﹣1＞0，x 2﹣1＞0，所以f （x 1）﹣f （x 2）＞0， 即f （x 1）＞f （x 2），故f （x ）在区间（1，+∞）上是单调递减函数；（2）由（1）知f （x ）在区间（1，+∞）上是单调递减，又f （2a +1）＞f （a +2）， 所以有{2a +1＜a +22a +1＞1解得0＜a ＜1，故a 的取值范围为（0，1）．21．（12分）设矩形ABCD （AB ＜AD ）的周长为36cm ，把△ACD 沿AC 向△ABC 折叠，AD 折过去后交BC 于点P ．当矩形ABCD 的边长为多少时，△ABP 的面积最大？并求出这个最大值． 解：设AD 翻折后，点D 的落点为D 1，则CD ＝CD 1，AD ＝AD 1， 所以在△ABP 和△CD 1P 中，有CD 1＝AB ，∠CPD 1＝APB ，∠D 1＝∠B ，所以△ABP ≅△CD 1P ，所以CP ＝AP ， 设AB ＝a ，BP ＝b ，则AP =√a 2+b 2=CP ，因矩形ABCD 周长为36cm ，所以AB +BC ＝18＝AB +BP +PC ， 所以a +b +√a 2+b 2=18，第11页（共11页） 由基本不等式可得18≥2√ab +√2ab =(2+√2)√ab ，当且仅当a =b =18−9√2时“＝”成立．此时√ab ≤18−9√2．故S △ABP =12ab ≤12×(18−9√2)2=81(3−2√2)，所以当矩形ABCD 的宽为18−9√2cm 时，S △ABP 的最大值为81(3−2√2)cm 2．22．（12分）设函数f （x ）＝x 2﹣tx +1，其中t ＞0．（1）若t ＝1，解关于x 的不等式mf （x ）＞x +m ﹣1（m ＞0）；（2）当x ∈[﹣1，3]时，f （x ）的最大值记为M （t ），最小值记为L （t ），求g （t ）＝M （t ）﹣L （t ）的解析式．解：（1）若t ＝1，则f （x ）＝x 2﹣x +1，∵mf （x ）＞x +m ﹣1（m ＞0）∴mx 2﹣（m +1）x +1＞0，方程mx 2﹣（m +1）x +1＝0的解为x 1=1，x 2=1m ， ∴当m ＝1时不等式的解集为{x |x ≠1}；当0＜m ＜1时，不等式的解集为{x|x ＜1或x ＞1m }；当m ＞1时，不等式的解集为{x|x ＜1m 或x ＞1}．（2）∵函数f （x ）的对称轴为x =−−t 2=t 2，①当t 2≤−1，即t ≤﹣2时，f （x ）在区间[﹣1，3]上是增函数， 所以M （t ）＝f （3）＝10﹣3t ，L （t ）＝f （﹣1）＝t +2，此时g （t ）＝M （t ）﹣L （t ）＝﹣4t +8； ②当−1＜t 2＜1，即﹣2＜t ＜2时，f （x ）在区间(−1，t 2)上单调递减，在区间[t 2，3)上单调递增，故L(t)=f(t 2)=−t 24+1，M(t)=f(3)=10−3t ，此时g(t)=M(t)−L(t)=−t 24−3t +9； ③当1≤t 2＜3，即2≤t ＜6时，f （x ）在区间(−1，t 2)上单调递减，在区间[t 2，3)上单调递增，所以M(t)=f(−1)=t +2，L(t)=f(t 2)=−t 24+1，此时g(t)=M(t)−L(t)=t 24+t +1； ④当t 2≥3，即t ≥6时，f （x ）在区间[﹣1，3]上是增函数， 所以M （t ）＝f （﹣1）＝t +2，L （t ）＝f （3）＝﹣3t +10，此时g （t ）＝M （t ）﹣L （t ）＝4t ﹣8．综上所述，g(t)={ −4t +8，t ≤−2t 24−3t +9，−2＜t ≤2t 24+t +1，2＜t ＜64t −8，t ≥6．。

2024年江苏省赣榆县第一中学数学高三上期末统考试题考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知复数()()2019311i i z i --=（i 为虚数单位），则下列说法正确的是（ ） A ．z 的虚部为4B ．复数z 在复平面内对应的点位于第三象限C ．z 的共轭复数42z i =-D．z =2．若复数12z i =+，2cos isin ()z ααα=+∈R ，其中i 是虚数单位，则12||z z -的最大值为( ) A1B．12C1D．123．某医院拟派2名内科医生、3名外科医生和3名护士共8人组成两个医疗分队，平均分到甲、乙两个村进行义务巡诊，其中每个分队都必须有内科医生、外科医生和护士，则不同的分配方案有 A ．72种B ．36种C ．24种D ．18种4．在复平面内，复数z =i 对应的点为Z ，将向量OZ 绕原点O 按逆时针方向旋转6π，所得向量对应的复数是（ ）A．12-+ B．12i C．12-- D．12i - 5．已知数列1a ，21a a ，32a a ，…，1n n a a -是首项为8，公比为12得等比数列，则3a 等于（ ）A ．64B ．32C ．2D ．46．中国古代数学著作《孙子算经》中有这样一道算术题：“今有物不知其数，三三数之余二，五五数之余三，问物几何？”人们把此类题目称为“中国剩余定理”，若正整数N 除以正整数m 后的余数为n ，则记为(mod )N n m =，例如112(mod3)=．现将该问题以程序框图的算法给出，执行该程序框图，则输出的n 等于（ ）．A ．21B ．22C ．23D ．247．下列命题中，真命题的个数为（ ） ①命题“若1122a b <++，则a b >”的否命题； ②命题“若21x y +>，则0x >或0y >”；③命题“若2m =，则直线0x my -=与直线2410x y -+=平行”的逆命题. A ．0B ．1C ．2D ．38．如图所示，矩形ABCD 的对角线相交于点O ，E 为AO 的中点，若(,)DE AB AD R λμλμ=+∈，则λμ+等于（ ）．A ．12-B ．12C ．1D ．1-9．已知平面向量a ，b 满足()1,2a =-，()3,b t =-，且()a ab ⊥+，则b =（ ） A ．3B 10C ．3D ．5102，体积为23，AB 、CD 是底面圆O 的两条互相垂直的直径，E 是母线PB 的中点，已知过CD 与E 的平面与圆锥侧面的交线是以E 为顶点的抛物线的一部分，则该抛物线的焦点到圆锥顶点P 的距离等于（ ）A ．12B ．1C ．104D ．5211．函数tan 42y x ππ⎛⎫=-⎪⎝⎭ 的部分图象如图所示，则 ()OA OB AB +⋅=（ ）A ．6B ．5C ．4D ．312．如果0b a <<，那么下列不等式成立的是（ ） A ．22log log b a < B ．1122b a⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭C ．33b a >D ．2ab b <二、填空题：本题共4小题，每小题5分，共20分。

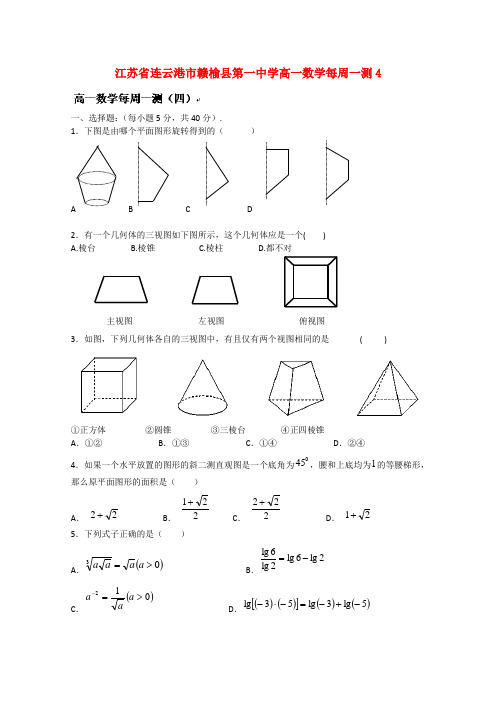
江苏省连云港市赣榆县第一中学高一数学每周一测4一、选择题：（每小题5分，共40分）.1．下图是由哪个平面图形旋转得到的（ ）B C D2．有一个几何体的三视图如下图所示，这个几何体应是一个( ) A.棱台 B.棱锥 C.棱柱 D.都不对3．如图，下列几何体各自的三视图中，有且仅有两个视图相同的是 ( )①正方体 ②圆锥 ③三棱台 ④正四棱锥 A ．①② B ．①③ C ．①④ D ．②④4．如果一个水平放置的图形的斜二测直观图是一个底角为045，腰和上底均为1的等腰梯形，那么原平面图形的面积是（ ）A ． 22+B ．221+ C ． 222+ D ． 21+ 5．下列式子正确的是（ ）A ．()03>=a a a aB ．2lg 6lg 2lg 6lg -=C ．()012>=-a aaD ．()()[]()()5lg 3lg 53lg -+-=-⋅-主视图 左视图 俯视图6．函数31-=-x a y 的图象恒过顶点坐标是（ ） A ．()3,1-B ．()2,1-C ．()3,2-D ．()2,2-7．函数()()1log 12--=x x f 的定义域是（ ）A ．()3,1B ．(]3,1C ．[]3,1D ．()+∞,18．)(x f 是定义在()2,2-上单调递减的奇函数，当0)32()2(<-+-a f a f 时，a 的取值范围是：（ ） A.()4,0B.⎪⎭⎫⎝⎛25,0 C.⎪⎭⎫ ⎝⎛25,21D.⎪⎭⎫ ⎝⎛25,1二、填空题：（每小题4分，共20分）．9．右图是一多面体的展开图，每个面内都给了字母，请根据要求回答问题：①如果A 是多面体的下底面，那么上面的面是 ；②如果面F 在前面，从左边看是面B ，那么上面的面是 ．10．若长方体的一个顶点上的三条棱的长分别为3,4,5，从长方体的一条对角线的一个端点出发,沿表面运动到另一个端点,其最短路程是______________。

图 2俯视图侧视图正视图江苏省连云港市赣榆县第一中学高一数学每周一测5一、选择题：（每小题5分，共40分）1、已知集合{}{},21|,0|≤≤-=>=x x B x x A 则B A Y =（ ）A 、{}1|-≥x xB 、{}2|≤x xC 、{}20|≤<x xD 、{}21|≤≤-x x2、2()23f x x mx =-+在[)2,-+∞上是增函数，在(),2-∞-上是减函数，则m =（ ） A. 2- B. 8- C. 2 D. 83.设()f x 是奇函数，且)()2(x f x f =+，当01x ≤≤时，()f x =2(1)x x -,则5()2f -=( ) A12-B 14-C 14D 124．如果x21log >0成立，则x 应满足的条件是( )D A ．x>12 B.12<x<1 C ．x<1 D ．0<x<15．若方程ax ＝x ＋a 有两解，则a 的取值范围为( ) A ．(1，＋∞) B ．(0,1) C ．(0，＋∞) D ．Ø6. 如图，一个骰子是由１～６六个数字组成，请你根据图中A ，B ，C 三种状态所显示的数字，推出“？”处的数字是（ ） Ａ．６ Ｂ．３ Ｃ．１ Ｄ．２7．直径为10cm 的一个大金属球，熔化后铸成若干个直径为2cm 的小球，如果不计损耗，可铸成这样的小球的个数为（ ） A ．5 B ．15 C ．25 D ．1258 如图1所示为一平面图形的直观图，则此平面图形可能是（ ）二、填空题（每小题4分，共20分）9．函数y x=-32的定义域是 .10. 由六个面围成的几何体，每个面都是矩形的几何体的名称 ． 11. 6．某三棱锥的三视图如图2所示，则该三棱锥的体积是ＡＢＣＤx '12已知1414log7,log5,a b==则用,a b表示35log28=13、设P是一个数集，且至少含有两个数，若对任意a、b∈P，都有a+b、a-b、ab、ab∈P（除数b≠0）则称P是一个数域，例如有理数集Q是数域，有下列命题：①数域必含有0，1两个数；②整数集是数域；③若有理数集Q⊆M,则数集M必为数域;④数域必为无限集.其中正确的命题的序号是.（把你认为正确的命题的序号都填上）三、解答题：（共40分）14、已知集合{}2|680A x x x=-+<，{}|()(3)0B x x a x a=--<，若A B A⋂=，求a 的取值范围15、如图，在四边形ABCD中，090DAB∠=，0135ADC∠=，5AB=，22CD=，2AD=，求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.16．已知：一个圆锥的底面半径为R，高为H，在其中有一个高为x的内接圆柱．（1）求圆柱的侧面积；（2）x为何值时，圆柱的侧面积最大．高一数学每周一测（五）答案 ABADA ADC9．（0，+∞） 10.长方体 11.31 12 b a a+-2 13、①④三、解答题：（共40分）14、解：由已知得A=（2，4）且A ⊆B若0<a ，则a a <3，得B=),3(a a )0,(-∞⊆，不合题意，舍去 若0=a ，则B=φ，不合题意，舍去 若0>a ，则a a 3<，得B=)3,(a a )4,2(⊇则有⎪⎩⎪⎨⎧≥≤>4320a a a ，解得a 的取值范围是]2,34[15.解：S S S S =++表面圆台底面圆台侧面圆锥侧面25(25)32222πππ=⨯+⨯+⨯+⨯⨯ 25(21)π=+V V V =-圆台圆锥222112211()331483r r r r h r h πππ=++-=16．解：（1）设内接圆柱底面半径为r.②①圆柱侧)(2x H H Rr Hx H R r x r S -=∴-=⋅=Θπ②代入①())0(2)(22H x Hx x H Rx H H R x S <<+-=-⋅=ππ圆柱侧（2）()S R H x Hx 圆柱侧=-+22π⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛--=42222H H x H R π22RH S H x π==∴圆柱侧最大时。

江苏省连云港市赣榆第一中学2024-2025学年高一上学期10月月考数学试题一、单选题1．命题“x ∀∈R ，210x x ++>”的否定为（ ） A ．x ∀∈R ，210x x ++≤B ．x ∀∉R ，210x x ++≤C ．0x ∃∉R ，2010x x ++> D ．0x ∃∈R ，2010x x ++≤2．设集合{2A |,{|10},x yB x x ==-<则A ∩B =（ ）A ．(-1，1)B ．(0，1)C ．(-1， +∞)D ．(0， +∞)3．以下五个写法中：①｛0｝∈｛0，1，2｝；②∅⊆｛0，2｝；③若0a b <<，则11a b<；④｛3，1，2｝＝｛2，3，1｝；正确的个数有（ ） A ．1个 B ．2个C ．3个D ．4个4．不等式403xx -≤+的解集是（ ） A ．{}|3x x <- B ．{}|4x x ≥C ．{}|34x x -<?D ．{|3x x <-或4}x ≥5．计算：0ln 221.1e 0.5lg 252lg 2-+-++=（ ） A ．0B ．1C ．2D ．36．设,a b R ∈，则“1a ≥，且1b ≥”是“2a b +≥”的 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件7．已知集合2{|320}M x x x =-+=、集合2{|350}N x x ax a =-+-=，若M N M ⋃=，则实数a 的取值集合为（ ）. A ．∅B ．{}210，C ．{|210}a a ≤<D ．{|210}a a <≤8．已知0x >，0y >，14121x y+=+，则2x y +的最小值是（ ） A ．3B ．94C ．8D ．9二、多选题9．满足{}{}13135,,,A =U 的集合A 可能是（ ） A ．{}5 B ．{}1,5 C ．{}3D ．{}1,3,510．下列各式或说法中正确的有（ ）A ．()lg lg100=B ．()lg ln 0e =C ．若10lg x =，则100x =D ．若251log ,2x =则5x =±11．下列结论中，错误的结论有（ ）A ．()43y x x =-取得最大值时x 的值为1B ．若1x <-，则11x x ++的最大值为2- C ．函数()2f x =2D ．若0a >，0b >，且2a b +=，那么12a b +三、填空题12．若()234log log log 0x =⎡⎤⎣⎦，则x =．13．若一个三角形的三边长分别为a ，b ，c ，记1()2p a b c =++，则此三角形面积S =△ABC 的周长为9，2c =，则()()p a p b -+-的值为，△ABC 的面积的最大值为．14．已知集合{}14A xx =-≤≤∣，集合{21}B x m x m =<<+∣，且,x B x A ∃∈∈为假命题，则实数m 的取值范围为.四、解答题15．已知{}2:560p A xx x =-+≤∣，(){}2:()0,1q B x x a x a a =--≤>∣. （1）若2a =，求集合A B U ；（2）如果q 是p 的必要条件，求实数a 的取值范围.16．计算：（1）2lg 2lg50lg 25lg 2++（） ； （2）若496a b ==，求11a b+的值．17．解答下列各题. (1)若3x >，求43x x +-的最小值. (2)若正数,x y 满足9x y xy +=， ①求xy 的最小值. ②求23x y +的最小值.18．南海九江中学为了宣传校园文化，由同学设计一幅九中文化矩形宣传画，要求画面面积为24000cm ，画面的上、下各留8cm 空白，左、右各留5cm 空白.如何设计画面的高与宽的尺寸，才能使宣传画所用纸张面积最小？19．设2(1)2y mx m x m =+-+-．(1)若不等式2y ≥-对一切实数x 恒成立，求实数m 的取值范围；(2)在（1）的条件下，求2251m m m +++的最小值；(3)解关于x 的不等式1y m <-．。

赣榆高级中学高一数学周练一 2017.9.15一、填空题（本大题共14小题，每小题5分，共 70分）1．已知集合{1,1,2,4},{1,0,2},A B =-=-则A B = ___ _________．2．若[]2,2U =-，[)1,2A =-，则U A =C _____ _________．3．已知集合2{|1}P x x =≤,{}M a =.若P M P = ,则a 的取值范围是_____ _________．4．下列各组函数中，表示同一函数的序号是_____ _________．①1y x =+ 和 211x y x -=+ ②0y x = 和 1y = ③2()f x x = 和()2()1g x x =+④()f x =和()g x =5．在映射:f A B →中，{}(,)|,A B x y x y R ==∈且:(,)(,)f x y x y x y →-+则与A 中的元素(1,2)-对应的B 中的元素为_____ _________．6.函数1y x =+的定义域为_____ _________．7．若)(x f 是满足14)]([-=x x f f 的一次函数，且在),(+∞-∞上是单调递减函数，则)(x f = __________．8．若()f x 的定义域为(]2,3-，则()()()F x f x f x =+-的定义域为_____ _________．9.函数{}1(221)1y x x x x x=∈-≠-+≤≤且的值域为_____ _________． 10.函数()f x =_____ _________．11.已知()f x =⎪⎩⎪⎨⎧≥<<--≤+)2(2)21()1(12x x x x x x ，若()3f x =, 则x 的值是_____ _________．12. 已知函数2()45f x x mx =-+在(,2)-∞-上是减函数，在(2,)-+∞上是增函数，则(1)f =_____ __．13.已知{}0232=+-=x ax x A ,若A 中至多有一个元素,则实数a 的取值范围是_____ _________．14．设集合34M x m x m ⎧⎫=+⎨⎬⎩⎭≤≤，13N x n x n ⎧⎫=-⎨⎬⎩⎭≤≤，且,M N 都是集合{}01x x ≤≤的子集，如果把b a -叫作集合{}x a x b ≤≤的“长度”，那么集合M N 的“长度”的最小值是_______．二．解答题：（共6题）15．（本题满分14分）已知集合}{}01)2(|{2a b x b x x A ==++++=，求集合}0|{2=++=b ax x x B 的真子集．16．（本题满分14分）求下列函数的值域:（1）12-+=x x y（2）123422--+-=x x x x y17．(本题满分16分) 设集合{}01922=-+-=a ax x x A ，{}0652=+-=x x x B ，{}0822=-+=x x x C ． (1)若B A =，求a 的值；(2)若φB A ，且φ=C A ，求a 的值；(3)若φ≠=C A B A ，求a 的值．18．（本题满分16分） 已知函数11()2f x mx nx =++(,m n 是常数)，且(1)2f =，11(2)4f =. （1）求,m n 的值；（2）当[)1,x ∈+∞时，判断()f x 的单调性并证明．。

江苏省赣榆县第一中学高一数学每周一测10一、选择题（本大题共8小题，每小题5分，共40分） 1. 直线1x =的倾斜角和斜率分别是（ ）A ． 045,1B ．0135,1-C ．090，不存在D ．0180，不存在 2.两平行直线1:3410l x y +-=与2:6850l x y +-=间的距离是（ ）A.45 B. 310C. 35D. 33．圆心为（－1， 2），半径为4的圆的方程是（ ）A ．(x +1)2 +(y －2) 2 =16B ．(x －1)2 +(y +2) 2 =16C ．(x +1)2 +(y －2) 2 =4D ．(x －1) 2 +(y +2) 2 =4 4．若A （－2，3），B （3，－2），C （21，ｍ）三点共线 则ｍ的值为（ ） Ａ．21 Ｂ．21- Ｃ．－2 Ｄ．25. 在长方体ABCD —''''A B C D 中，AB =AD ='1AA =，则'AA 和'BC 所成的角是（ ）A.60°B.45°C.30°D.90°6. 下列命题中a 、b 、c 表示直线，αβγ、、表示直线平面，正确的是（ ）A.若//,//a b ββ，则 //a b .B.若,αγβγ⊥⊥，则//αβ.C.若,,m n αβαβ⊥⊂⊂，则m n ⊥.D.若m ⊥α，n ⊥m ，n α⊄，则//n α.7. 方程022=++-+m y x y x 表示一个圆，则m 的取值范围是（ ） A ．2≤m B ．m ＜21 C ．m ＜2 D ．21≤m8．一个几何体的三视图如图所示：俯视图是边长为2的正方形，主视图与左视图是全等的等腰直角三角形(单位长度: cm), 则此几何体的全面积是（ ）A.28cm B.24cm C.2(4cm + D.2 二、填空题（本题共5小题，每小题4分，共20分）9．已知⎩⎨⎧∈--∈=]3,0(3]0,3[3)(x x x x f x ，则=))2((f f10．已知32)(2-+-=mx x x f 在[2，+∞）上为减函数，则m 的取值范围是 11.点A （1，0）到直线230x y ++=的距离是 ． 12.直线210mx y m ++-=恒过定点13.圆221x y +=上的点到直线8x y -=的距离的最小值 ．高一每周一测（十）答题卷一、选择题：二、填空题：9． 10． 11。

2024-2025学年江苏省赣榆高级中学、南京市第五中学高一上学期10月月考数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.设集合A={0,1,2,3,4,5}，集合B={2,3,4}，则∁A B=( )A. {0,1}B. {1,5}C. {0,1,5}D. {0,1,2,3,4,5}2.不等式−x2+2x−4>0的解集为( )A. RB. ⌀C. {x|x>0,x∈R}D. {x|x<0,x∈R}3.若命题“∀x∈R,x2+1>m”是真命题，则实数m的取值范围是( )A. (−∞,1]B. (−∞,1)C. [1,+∞)D. (1,+∞)4.若y1=3x2−x+1，y2=2x2+x−1，则y1与y2的大小关系是( )A. y1<y2B. y1=y2C. y1>y2D. 随x值变化而变化5.若直角三角形的面积为50，则两条直角边的和的最小值是( )A. 52B. 102C. 10D. 206.使“x≤−12或x≥3”成立的一个充分不必要条件是( )A. x<0B. x≥0C. x∈{−1,3,5}D. x≤−12或x≥37.下列命题中正确的是( )A. 若ab>0，a>b，则1a <1bB. 若a<b，则ac2<bc2C. 若a>b，c>d，则a−c>b−dD. 若a>b，c<d，则ac >bd8.下列说法正确的是( )A. 函数y=4x2+9x2的最小值是6B. 正数x，y满足2x +8y=1，则xy的最大值是64C. 函数y=2−3x−4x(x>0)的最小值是2−43D. 若x>−1，则函数y=x+1x+1取到最小值时x=0二、多选题：本题共3小题，共18分。

在每小题给出的选项中，有多项符合题目要求。

9.命题p:∃x∈R,x2+bx+1≤0的否定是真命题，则实数b的值可能是( )A. −74B. −32C. 2D. 5210.设正实数a ，b 满足a +b =1，则( )A. 1a +1b 有最小值4B. ab 有最小值12C. a + b 有最大值 7D. a 2+b 2有最小值1211.关于x 的不等式ax 2+bx +c ≥0的解集为{x|x ≤−1或x ≥4}，下列说法正确的是( )A. a >0B. 不等式cx 2−bx +a <0的解集为{x|−14<x <1}C. 3b +c 的最大值为−4D. 关于x 的不等式x 2+bx +c <0解集中仅有两个整数，则a 的取值范围是(17,25]三、填空题：本题共3小题，每小题5分，共15分。