2013-2016年全国卷知识点分类汇总(理科)
- 格式:pdf
- 大小:56.87 KB
- 文档页数:4


2013年高考真题理科数学分类汇编(解析版)函 数1、(2013年高考(安徽卷))函数=()y f x 的图像如图所示,在区间[],a b 上可找到(2)n n ≥个不同的数12,...,,n x x x 使得1212()()()==,n nf x f x f x x x x 则n 的取值范围是 (A ){}3,4 (B ){}2,3,4(C ){}3,4,5 (D ){}2,3【答案】B【解析】由题知,过原点的直线与曲线相交的个数即n 的取值.用尺规作图,交点可取2,3,4. 所以选B2、(2013年高考(北京卷))函数f(x)的图象向右平移一个单位长度,所得图象与y=e x 关于y 轴对称,则f(x)= A.1ex + B.1e x - C. 1e x -+ D. 1e x --3、(2013年高考(广东卷))定义域为R 的四个函数3y x =,2x y =,21y x =+,2sin y x =中,奇函数的个数是( )A . 4B .3C .2D .【解析】C ;考查基本初等函数和奇函数的概念,是奇函数的为3y x =与2sin y x =,故选C .4、(2013年高考(全国(广西)卷))已知函数()()()-1,021f x f x -的定义域为,则函数的定义域为(A )()1,1- (B )11,2⎛⎫- ⎪⎝⎭ (C )()-1,0 (D )1,12⎛⎫⎪⎝⎭【答案】B【解析】由题意可知1210,x -<+<,则112x -<<-。
故选B5、(2013年高考(全国(广西)卷))函数()()1=log 10f x x x ⎛⎫+> ⎪⎝⎭的反函数()1=f x -(A )()1021x x >- (B )()1021xx ≠- (C )()21x x R -∈ (D )()210x x ->【答案】A【解析】由题意知1112(0)21y y x y x +=⇒=<-, 因此,故选A6、(2013年高考(全国(广西)卷))若函数()211=,2f x x ax a x ⎛⎫++∞ ⎪⎝⎭在是增函数,则的取值范围是(A )[]-1,0 (B )[]-∞1, (C )[]0,3 (D )[]3∞,+7、(2013年高考(湖南卷))函数()2ln f x x =的图像与函数()245g x x x =-+的图像的交点个数为A .3B .2C .1D .0【答案】B【解析】画出两个函数的图象,可得交点数。



2013年全国高考理科数学分类汇编一、集合与简易逻辑辽宁2013(2)已知集合{}{}4|0log 1,|2A x x B x x AB =<<=≤=,则A .()01,B .(]02,C .()1,2D .(]12, 辽宁2013(4)下面是关于公差0d >的等差数列()n a 的四个命题:{}1:n p a 数列是递增数列;{}2:n p na 数列是递增数列; 3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列;{}4:3n p a nd +数列是递增数列; 其中的真命题为(A )12,p p (B )34,p p (C )23,p p (D )14,p p 江西2013.1.已知集合M={1,2,zi},i ,为虚数单位,N={3,4},则复数z=A.-2iB.2iC.-4iD.4i 全国1.1、已知集合A={x |x 2-2x >0},B={x |-5<x <5},则 ( ) A 、A∩B=∅ B 、A ∪B=R C 、B ⊆A D 、A ⊆B全国2.1.已知集合{}{}3,2,1,0,1,,4)1(|2-=∈<-=N R x x x M ,则=⋂N M ( )A {}2,1,0B {}2,1,0,1-C {}3,2,0,1-D {}3,2,1,0北京2013.1.已知集合A={-1,0,1},B={x |-1≤x <1},则A∩B= ( ) A.{0} B.{-1,0} C.{0,1} D.{-1,0,1}四川1.设集合{|20}A x x =+=,集合2{|40}B x x =-=,则AB =( )(A ){2}- (B ){2} (C ){2,2}- (D )∅ 重庆(1)已知集合{1,2,3,4}U =,集合={1,2}A ,={2,3}B ,则()U AB =ð(A ){1,3,4} (B ){3,4} (C ){3} (D ){4} 天津卷(1) 已知集合A = {x ∈R | |x |≤2}, A = {x ∈R | x ≤1}, 则A B ⋂= (A) (,2]-∞ (B) [1,2] (C) [-2,2] (D) [-2,1]2013安微(1)设集合{}{}{}1,2,3,4,5,|,,,A B M x x a b a A b B ====+∈∈则M 中元素的个数为(A )3 (B )4 (C )5 (D )6山东(2)设集合A={0,1,2},则集合B={x-y|x ∈A, y ∈A }中元素的个数是( )A. 1B. 3C. 5D.9重庆(2)命题“对任意x R ∈,都有20x ≥”的否定为(A )对任意x R ∈,使得20x < (B )不存在x R ∈,使得20x <(C )存在0x R ∈,都有200x ≥ (D )存在0x R ∈,都有200x <2013广东1.设集合M={x ∣x 2+2x=0,x ∈R},N={x ∣x 2-2x=0,x ∈R},则M ∪N= A. {0} B. {0,2} C. {-2,0} D {-2,0,2} 北京2013.3.“φ=π”是“曲线y=sin(2x +φ)过坐标原点的” A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件四川4.设x Z ∈,集合A 是奇数集,集合B 是偶数集.若命题:,2p x A x B ∀∈∈,则( ) (A ):,2p x A x B ⌝∃∈∉ (B ):,2p x A x B ⌝∀∉∉ (C ):,2p x A x B ⌝∃∉∈ (D ):,2p x A x B ⌝∃∈∈2013广东8.设整数n ≥4,集合X={1,2,3……,n }。
考点25 数列求和及综合应用一、选择题1。
(2013·新课标Ⅰ高考理科·T12)设△A n B n C n 的三边长分别为a n ,b n ,c n ,△A n B n C n 的面积为S n ,n =1,2,3,…若b 1>c 1,b 1+c 1=2a 1,a n +1=a n ,b n +1=错误!,c n +1=错误!,则( )A 、{S n }为递减数列B 、{S n }为递增数列C 、{S 2n -1}为递增数列,{S 2n }为递减数列D 、{S 2n -1}为递减数列,{S 2n }为递增数列 【解析】选B.因为n n a a=+1,21nn n a c b +=+,21nn n a b c+=+,所以1a an=,++1n b =+1n c 2n n a c +2n n a b ++1)(21)(21a c b a c b n n n n n ++=++= ++1n b )2(212111a c b a c n n n -+=-+,注意到1112a c b =+,所以12a c b n n =+. 于是nnnC B A ∆中,边长1a C B nn=为定值,另两边的长度之和为12a c b n n =+为定值。
因为-+1n b =+1n c 2n n a c +2n n a b +-)(21n n c b --=, 所以)()21(111c b c bn nn --=--,当+∞→n 时,有0→-n n c b ,即n n c b →,于是n n n C B A ∆的边n n C B 的高n h 随n 增大而增大,于是其面积n n n n n h a h C B S 121||21==为递增数列. 二、填空题2。
(2013·新课标Ⅰ高考理科·T14)若数列}{na 的前n 项和3132+=n na S,则}{na 的通项公式是=na _________【解题指南】先利用S 1=a 1求出a 1的值,再利用S n —S n —1=a n 求出通项公式a n 。
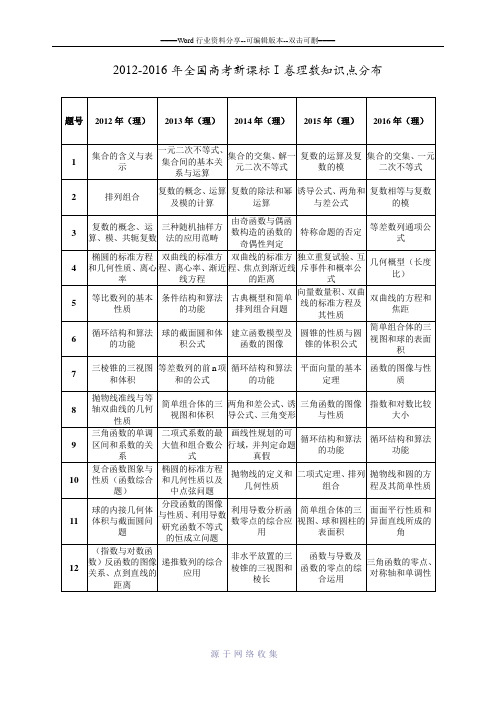
2013~2016新课标I理科数学
考点分布及考点分析
一.考点分布
二.考点分析
①常考考点:二次不等式、集合;复数运算;程序框图;计数原理的应用;平面向量基本运
算;线性规划;数列的基本运算;和差角倍角公式的应用;解三角形;导数的
简单应用(如切线问题与构造法解不等式)与综合应用;椭圆背景下的综合应
用;双曲线的几何性质;抛物线的定义;函数的图像与性质(特别是奇偶性与
对称性);三角函数的图像(图像变换)与性质(特别是奇偶性与对称性、最
值);解三角形;三种方程的互化及其应用等.
②轮换考点:概率(互斥事件、独立事件、古典概型、几何概型、)与统计(直方图、条形
图、正态分布、回归分析、分布列与期望)问题;平行与垂直;二面角、线面
角及异面直线所成的角;圆与球;第17题大题:解三角形与数列;绝对值不
等式与基本不等式等.
③不常考但必须掌握的考点:逻辑推理;折叠问题;截面问题;茎叶图;条件概率;随即模
拟拟;独立性检验;抽象函数的性质;各种应用性问题等.
④创新问题:数学史;概率与统计;空间想象能力的考查;导数的简单应用,三角函数的性
质与解三角形;函数的对称性应用等.
⑤改变传统:向量问题;空间想象能力及几何法推理的考查;动手作图能力;概率与统计问
题;数学史;函数的性质;计数原理;文字题的推理;轨迹问题;数列的解答
题;解三角形;树立对平面解析几何的信心;积累函数与导数综合问题的解题
技巧等.
⑥对小题中的11,12,16题,尽量回避直接法求解,一般均可以用间接法求解,考查学生的
反应速度和处理问题的应变能力也是高考考查的一方面.
⑦所谓的难题必然与数学思想相融合,分析问题时注意从数学思想方面切入.。
全国高考新课标卷数学考点梳理
表二:2013年—2015年全国新课标理科数学卷Ⅰ与卷Ⅱ考点对比
重庆卷与全国卷的简单比较
1.试卷结构不同:
重庆卷:选择题共10题,填空题有3选2,解答题没有选作题
全国卷:选择题共12题,填空题取消3选2,解答题最后增加了3选1(内容与重庆填空题中的3选2相同)
2.试卷难易设置不同:
重庆卷:选择题基础题多,区分度不大,难题的难度大;解答题压轴题基本上是数列与不等式,入手难。
2015年理数难度系数为0.69,文数难度系数为0.58.
全国卷:选择题基础题少,中档题多,难题比重庆题易于入手,遵循“易有新意,难有道理”;解答题压轴题基本上利用导数研究函数切线方程、单调性、最值应用等,若在时间允许的情况下学生能够入手。
一般来说,全国新课标卷Ⅰ比全国新课标卷Ⅱ略难,但有时也可能变化,如2015年全国新课标卷Ⅰ难度系数为0.54,全国新课标卷Ⅱ难度系数为0.52.,
3.试题考点考查:
重庆卷:解答题较固定,应用题一般考离散型随机变量分布列、期望、方差等
全国卷:解答题第17题可能考查三角与数列中的之一,应用题可能是统计、回归分析、列联表和离散型随机变量分布列、期望、方差等,形成统计与概率模式。