三角形高程拟合方法

§5.9 三角高程测量三角高程测量的基本思想是根据由测站向照准点所观测的垂直角（或天顶距）和它们之间的水平距离，计算测站点与照准点之间的高差。

这种方法简便灵活，受地形条件的限制较少，故适用于测定三角点的高程。

三角点的高程主要是作为各种比例尺测图的高程控制的一部分。

一般都是在一定密度的水准网控制下，用三角高程测量的方法测定三角点的高程。

5.9.1 三角高程测量的基本公式1.基本公式关于三角高程测量的基本原理和计算高差的基本公式，在测量学中已有过讨论，但公式的推导是以水平面作为依据的。

在控制测量中，由于距离较长，所以必须以椭球面为依据来推导三角高程测量的基本公式。

如图5-35所示。

设0s 为B A 、两点间的实测水平距离。

仪器置于A 点，仪器高度为1i 。

B 为照准点，砚标高度为2v ，R 为参考椭球面上B A ''的曲率半径。

AF PE 、分别为过P 点和A 点的水准面。

PC 是PE 在P 点的切线，PN 为光程曲线。

当位于P 点的望远镜指向与PN 相切的PM 方向时，由于大气折光的影响，由N 点出射的光线正好落在望远镜的横丝上。

这就是说，仪器置于A 点测得M P 、间的垂直角为2,1a 。

由图5-35可明显地看出，B A 、 两地面点间的高差为NB MN EF CE MC BF h --++==2,1 （5-54）式中，EF 为仪器高NB i ;1为照准点的觇标高度2v ；而CE 和MN 分别为地球曲率和折光影响。

由2021s R CE =2021s R MN '= 式中R '为光程曲线PN 在N 点的曲率半径。

设,K R R='则 20202.21S RK S R R R MN ='=K 称为大气垂直折光系数。

图5-35由于B A 、两点之间的水平距离0s 与曲率半径R 之比值很小（当km s 100=时,0s 所对的圆心角仅5'多一点），故可认为PC 近似垂直于OM ，即认为 90≈PCM ,这样PCM ∆可视为直角三角形。

几种高程拟合方法的精度分析高程拟合方法是地理信息系统（GIS）中的重要内容，在数字地形模型（DTM）生成、地形分析和地貌描述等领域具有广泛应用。

不同的高程拟合方法会影响到地形模型的精度，因此对于不同高程拟合方法的精度进行分析是很有意义的。

以下是几种常见的高程拟合方法及其精度分析：1.插值法插值法是一种常见的高程拟合方法，在实际应用中被广泛使用。

常见的插值方法包括反距离加权插值法、克里金插值法以及样条插值法等。

插值法的精度受到原始高程数据的密度和分布情况的影响。

如果原始高程数据密度较高且分布均匀，插值法可以获得较高的精度。

然而，在原始高程数据密度较低或分布不均匀的情况下，插值法可能会出现插值误差较大的问题，拟合结果的准确性会受到一定的限制。

2.拟合曲面法拟合曲面法是一种通过拟合曲线或曲面来估计高程的方法。

常见的拟合曲面方法包括最小二乘法、多项式拟合、平滑拟合以及基于回归分析的方法等。

拟合曲面法的精度取决于所选择的拟合函数和选择的拟合点。

如果使用复杂的拟合函数和足够多的拟合点，可以获得较高的精度。

然而，过度复杂的拟合函数可能导致过度拟合的问题，而拟合点过少可能会导致低精度。

3.网格法网格法是一种将区域划分成网格并在每个网格上估计高程的方法。

常见的网格法包拟合方法包括反距离加权平均法、泰森多边形法以及贝叶斯方法等。

网格法的精度取决于网格的大小和形状，以及对于每个网格所采用的高程估计方法。

如果网格足够小且形状合理，并选择合适的高程估计方法，可以获得较高的精度。

然而，网格法可能会导致插值误差在网格边界处积累的问题，从而影响到拟合结果的准确性。

4.三角形不规则网法三角形不规则网法是一种通过构建不规则三角形网格来估计高程的方法。

该方法通过对于不规则三角形内插值来估计高程。

三角形不规则网法的精度取决于网格的划分方法和插值方法。

如果网格的划分合理且插值方法准确，可以获得较高的精度。

然而，三角形不规则网法可能会导致网格形状不规则或者包含过多狭长的三角形，从而影响到拟合结果的精度。

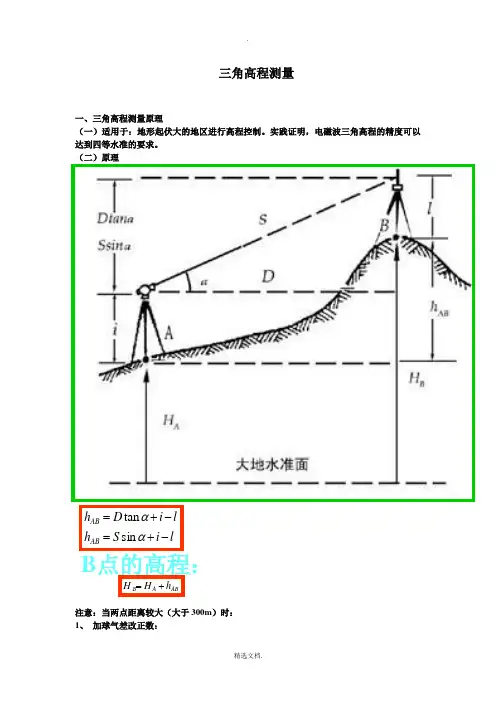
三角高程测量
一、三角高程测量原理
（一）适用于：地形起伏大的地区进行高程控制。

实践证明，电磁波三角高程的精度可以达到四等水准的要求。

（二）原理
注意：当两点距离较大（大于300m ）时：
1、 加球气差改正数：
B 点的高程：
AB A B h H H += l
i S h l i D h AB AB -+=-+=ααsin tan
即有： 2、可采用对向观测后取平均的方法，抵消球气差的影响。

球差为正，气差为负
二、三角高程测量的观测和计算
①安置经纬仪于测站上，量取仪高i 和目标高s 。

读 至0.5cm ，量取两次的结果之差≤1cm 时，取平均值。

②当中丝瞄准目标时，将竖盘指标水准管气泡居中，读取竖盘读数。

必须以盘左、盘右进行观测。

③竖直角观测测回数与限差应符合规定。

④用电磁波测距仪测量两点间的倾斜距离D ’，或用三角测量方法计算得两点间的水平距离D 。

f
l Dtg i h AB +-+=α即有： R
D f 243.0=。

全站仪如何进行三角高程测量使用跟踪杆配合全站仪测量高程的方法越来越普及，使用传统的三角高程测量方法已经显示出了它的局限性。

经过长期摸索，总结出一种新的方法进行三角高程测量。

这种方法既结合了水准测量的任一置站的特点，又减少了三角高程的误差来源，同时每次测量时还不必量取仪器高、棱镜高。

使三角高程测量精度进一步提高施测速度更快。

在工程施工的过程中，常常涉及到高程测量。

传统的测量方法是水准测量、三角高程测量。

两种方法虽然各有特色，但都存在着不足。

水准测量是一种直接测高法，测定高差的精度是较高的，但水准测量受地形起伏的限制，外业工作量大，施测速度较慢。

三角高程测量是一种间接测高法，它不受地形起伏的限制，且施测速度较快。

在大比例地形图测绘、线型工程、管网工程等工程测量中广泛应用。

但精度较低且每次测量都得量取仪器高，棱镜高，麻烦而且增加了误差来源。

一、三角高程测量的传统方法如图一所示，设A，B为地面上高度不同的两点。

已知A点高程HA，只要知道A点对B点的高差HAB即可由HB=HA+HAB得到B 点的高程HB。

图一图中：D为A、B两点间的水平距离。

а为在A点观测B点时的垂直角i为测站点的仪器高，t为棱镜高HA为A点高程，HB为B点高程。

V为全站仪望远镜和棱镜之间的高差（V=Dtanа）。

首先假设A，B两点相距不太远，也不考虑大气折光的影响。

为了确定高差hAB，可在A点架设全站仪，在B点竖立跟踪杆，观测垂直角а，并直接量取仪器高i和棱镜高t，若A，B两点间的水平距离为D，则hAB=V+i-t故HB=HA+Dtanа+i-t。

（1）这就是三角高程测量的基本公式，但它是以水平面为基准面和视线成直线为前提的。

因此，只有当A，B两点间的距离很短时，才比较准确。

当A，B 两点距离较远时，就必须考虑地球弯曲和大气折光的影响了。

这里不叙述如何进行球差和气差的改正，只就三角高程测量新法的一般原理进行阐述。

从传统的三角高程测量方法中可以看出，它具备以下两个特点：1、全站仪必须架设在已知高程点上2、要测出待测点的高程，必须量取仪器高和棱镜高。

摘要在工程建设的勘测、施工中常常涉及到高程测量，现场采用的测量方法主要是水准测量和三角高程测量。

水准测量精度高，但是速度比较慢，效率低。

此外，水准测量的转点多，而且标尺与仪器也存在下沉误差，如果在丘陵、山区等地使用水准测量进行高程传递是非常困难的，有时甚至是不可能的。

近些年来，由于全站仪的发展，使得测角、测距的精度不断提高。

三角高程测量传递高程比较灵活、方便、受地形条件限制较少等优点，因此全站仪三角高程测量补充了水准测量不能在山区等地形起伏较大的地区施测的不足，成为水准测量的重要方法。

本文对全站仪三角高程测量的原理、方法、精度等进行了分析，认为用全站仪代替水准仪进行高程测量，在一定范围内可达到三等水准测量要求。

关键词：全站仪三角高程精度分析等级水准AbstractIn the construction survey, construction often involve the height measurement, the scene is the leveling measurement method is mainly used and trigonometric leveling. Leveling precision, but at a slower speed, low efficiency. In addition, the turning point of leveling and gauge and instrument is also sinking error, if in the hills, mountains and other places using the leveling elevation transfer is very difficult, sometimes even impossible. In recent years, due to the development of the total station, the accuracy of Angle, distance to improve. Trigonometric leveling elevation is more flexible and convenient, and the advantages of less restricted by terrain conditions, so the triangle elevation surveying added leveling can't in mountainous terrain volatile regions such as measured by the insufficiency, has become an important method of leveling. In this paper, the principle and method of total station triangle elevation measurement, precision are analyzed, such as that using total station to replace the level height measurement, within a certain range can be up to three, the fourth level measurement requirements.Key Words:Total station, Triangle elevation, Accuracy analysis, Order leveling目录摘要 (I)ABSTRACT (II)第1章绪论 (1)1.1 前言 (1)1.1.1 研究目的与意义 (1)1.2 国内外研究现状 (2)1.2.1 国内研究现状 (2)1.2.2 国外研究现状 (2)1.3 本文研究内容 (3)第2章全站仪三角高程测量原理和观测方法 (4)2.1 全站仪三角高程的基本理论 (4)2.1.1 全站仪三角高程测量的原理 (4)2.1.2三角高程测量的基本公式 (5)2.2 全站仪三角高程测量的方法 (7)2.2.1对向观测法 (7)2.2.2中间测量法 (8)第3章三角高程与几何水准高程误差及精度的对比研究 (9)3.1 全站仪对向观测法的精度分析 (9)3.2 全站仪中间观测法的精度分析 (11)3.3 三角高程测量方法的比较 (13)第4章实例分析 (15)4.1 测量过程 (15)4.2 观测结果分析 (17)第5章结论与展望 (19)致谢 (20)参考文献 (21)第1章绪论1.1 前言测量地面待定点的高程，传统的方法是通过仪器测量待测点与已知点间的高差，然后计算出待测点的高程。

几种高程拟合方法的精度分析高程拟合是指根据采样点或测量点的高程数据，通过其中一种数学模型拟合出地面表面的高程分布。

高程拟合在地理信息系统(GIS)、地形分析、水文模拟、三维模型建立等领域具有广泛的应用。

高程拟合的精度分析是评价拟合结果与实际地形之间的差距，并确定拟合方法的准确性和适用性的重要步骤。

以下是几种高程拟合方法的精度分析：1.反距离加权法(IDW)：反距离加权法是一种常见的高程拟合方法，根据采样点之间的距离和权重来计算未知点的高程。

在精度分析中，可以通过交叉验证方法来评估不同的幂指数对拟合结果的影响。

通过计算实际测量值与拟合结果之间的误差，可以评估反距离加权法的精度。

2.三角网法(TIN)：三角网法是一种通过构建三角形网格来拟合地形表面的方法。

在精度分析中，可以通过将已知点与拟合结果进行比较，计算高程差值来评估拟合的精度。

此外，还可以使用均方根误差(RMSE)来评估TIN模型是否与实际地形相匹配。

3. 克里金法(Kriging)：克里金法是一种基于地理变量之间的相似性进行插值的方法，可以用于高程拟合。

在精度分析中，可以通过交叉验证方法或留一验证方法来评估不同的插值参数对拟合结果的影响。

通过计算实际测量值与拟合结果之间的偏差，可以评估克里金法的精度。

4.多项式插值法：多项式插值法是一种利用多项式函数进行高程拟合的方法。

在精度分析中，可以通过计算实际测量值与拟合结果之间的残差来评估多项式插值法的精度。

此外，还可以使用拟合曲线与实际测量值之间的拟合度来评估多项式插值法的准确性。

综上所述，对于高程拟合方法的精度分析，可以通过比较实际测量值和拟合结果之间的误差、计算高程差值、计算均方根误差(RMSE)、计算偏差或残差等指标来评估拟合的准确性和适用性。

不同的拟合方法适用于不同的应用场景，根据实际需要选择最合适的方法。

目录1.引言 (2)2.三角高程测量计算基本公式 (2)2. 1传统三角高程测量计算基本公式 (2)2.2自由设站测量三角高程计算基本公式 (2)2.2.1自由设站的概念 (2)2.2.2公式推导 (3)3.自由设站测量三角高程法在公路工程施工测量中的应用 (3)3.1 在路基放样施工标高中的应用 (3)3.2在高填方路基或路堑高边坡（以下统称为高边坡）垂直位移监测的应用。

34.结论 (4)全站仪自由设站测量三角高程的方法马炳明（广东省龙浩路桥有限公司，广东省，广州510630）摘要文章简要介绍了全站仪自由设站测量三角高程的方法及其在公路工程施工测量中的应用关键词全站仪、三角高程、自由设站、竖直角1.引言随着土木工程建设的发展，全站仪的广泛应用，一些新的测量方法应运而生，全站仪自由设站测量三角高程法就是其中的一种。

在此，笔者主要浅谈在单向观测和不考虑球气差改正的情况下，用全站仪自由设站测量三角高程的方法及其在公路工程施工测量中的应用。

2.三角高程测量计算基本公式2. 1传统三角高程测量计算基本公式H B= H A+ i+ S *sin a—j⑴上式就是传统三角高程测量计算基本公式，式中各符号含义如下（假设全站仪架设在A点，要测B点的高程）：H B—待测点B的高程；H A—已知水准点A的高程；i—全站仪望远镜旋转轴中心的高度；S —全站仪望远镜旋转轴中心到B点棱镜中心的斜距；a—在A 点观测B点的竖直角；j—B点处棱镜中心的高度。

在施工放样时，如直接测出全站仪望远镜旋转轴中心到B点棱镜中心的高差V，则V = S *sin a，将V代入⑴式，得H B= H A+ i+ V—j⑵2.2自由设站测量三角高程计算基本公式2.2.1自由设站的概念自由设站是测量中架设仪器的一种方法，全站仪后方交会使用的就是这种方法。

而三角高程测量的自由设站是相对于传统三角高程测量时固定在水准点上设站而言。

2.2.2公式推导CA全站仪自由设站测量三角高程法示意图如上图，A点为已知高程为H A的后视水准点，B点为前视待测点，设其高程为H B，分别在A、B两点架设装有棱镜的对中杆，它们的棱镜中心分别为I、J，镜高分别为i、j。

浅析在工程测量中GPS高程拟合方法摘要：GPS由于布网灵活、简捷、经济已经广泛应用与工程建设中，GPS测量精度高、速度快、方便实用，具有很高的平面精度，但是GPS高程应用问题，目前仍在进一步探讨之中。

因为利用GPS测量所得到的高程是地面点的大地高，工程中需要把GPS高程测量的大地高转换为正常高。

关键字：GPS；高程拟合；正常高1 引言在工程测量中，高程测量是工程测量中一项重要的内容。

目前，高程的测量方法主要有以下四种：几何水准测量、三角高程测量、重力高程测量、GPS高程测量。

传统的几何水准测量虽然精度高，但耗时长、耗费多、工作效率低。

GPS 由于自身测量精度高、速度快、工作效率高等优点被广泛应用于高程测量。

GPS 测量的高程是在WGS-84坐标系下的大地高[1]，大地高是地面一点沿参考椭球面的法线到参考椭球面的距离，用符号H表示。

实际应用中需要把GPS测得的大地高转换为正常高，正常高是地面点到通过该点的铅垂线与似大地水准面的交点的距离，用符号H r表示。

似大地水准面到参考椭球面之间的距离称为高程异常，用符号ζ表示。

因此大地高与正常高之间的关系为：ζ=H-H r(1)2 三种高程系统2.1大地高系统以参考椭球面为高程基准面的高程系统，称为大地高系统。

这个系统的高程，是地面点沿法线方向到参考椭球面的距离，称为大地高，通常用表示。

大地高系统只有几何意义，不具有物理意义，同一个点在不同的参考椭球下，具有不同的大地高，这个系统的高差，是两地面点大地高之差，称为大地高高差。

大地高可由 GPS技术直接测定，也可由几何和物理大地测量相结合的方法来测定。

2.2正高系统大地测量学所研究的是在整体上非常接近于地球自然表面的水准面，设想与平均海水面相重合，不受潮汐、风浪及大气压变化的影响，并延伸到大陆下面与铅垂线相垂直的水准面称为大地水准面，它是一个没有褶皱、无菱角的连续封闭曲面。

正高系统就是以大地水准面为基准面的高程系统。

基于GPS的高程拟合方法研究随着GPS技术的发展和应用的广泛，越来越多的地理信息可以通过GPS定位得到。

其中一个重要的应用领域是高程测量。

GPS可以提供三维空间中点的经纬度和高程信息，但是由于多种因素的影响，GPS测得的高程数据存在一定的误差。

为了改善GPS高程数据的精度，需要进行高程拟合。

高程拟合是利用已知高程数据来估计未知位置的高程值的过程。

在拟合过程中，需要考虑空间相邻点之间的高程关系。

常见的高程拟合方法有以下几种：三角网法、克里金插值法、多项式拟合法等。

三角网法是一种比较常用的高程拟合方法。

该方法基于三角形相似原理，根据邻近点之间的距离和高程差，估计未知点的高程。

三角网法可以通过建立三角形网格来进行高程插值，并且可以根据实际情况调整三角形的形状和大小，以适应不同的地形。

克里金插值法是一种基于空间半变函数的高程拟合方法。

该方法通过计算样本点之间的相互关系来估计未知点的高程。

在克里金插值法中，可以通过拟合半变函数来对空间点之间的关系进行建模，从而提高拟合效果。

该方法的优点是可以考虑样本点之间的相关性，并且可以根据样本点的权重进行拟合。

多项式拟合法是一种简单但有效的高程拟合方法。

该方法通过拟合多项式曲线来估计未知点的高程。

多项式拟合法可以根据实际情况选择合适的多项式阶数，以适应不同的地形。

该方法的优点是计算简单，但需要充分考虑样本点的分布和拟合误差。

高程拟合是一种基于GPS数据的高程估计方法。

常见的高程拟合方法包括三角网法、克里金插值法和多项式拟合法。

这些方法可以根据实际情况选择合适的方法，并结合其他辅助数据来提高高程数据的精度。