当前位置：文档之家 › 第二章热力学第一定律演示文稿

第二章热力学第一定律演示文稿

  • 格式：ppt
  • 大小：1.98 MB
  • 文档页数：74

下载文档原格式

  / 74

合集下载

物理化学 第二章 热力学第一定律.ppt

物理化学 第二章 热力学第一定律.ppt
第二章 热力学第一定律 （The first law of
thermodynamics）
◆“化学热力学”概念 一、热力学研究的内容
1、 化学反应的能量转化规律（热一律）； 2、 化学反应的可能性和限度（热二律）； 二、特点
1、 研究物质的宏观性质； 2、 只考虑变化的始终态； 3、 解决最大产率，没有时间的概念； 三、局限性
系统分三类： 1）封闭系统； 2）敞开系统； 3）隔离系统；
2、系统的宏观性质：
广延性质：数量与物质的量有关，具有加和性。
如：m、V、U、H等。
强度性质：数量与物质的量无关，不具有加和
性。如：T、P、d等。
3、状态、状态性质和状态函数
状态：系统中物理、化学性质的综合表现。当
这些性质具有确定的值时，系统就处于某一状态 。
3.3 过程热的计算 恒容变温过程的热：
δQ v=n CV，M dT
恒压变温过程的热：
δQ P=n CP，M dT
组成不变的均相系统等压（等容）变
T2

T1
T2

温过程热的计算
T1
Qp

H

n
T2 T1
C
p,m
dT
QV
U
n
T2 T1
CV
,mdT
例题：试计算常压下1molCO2温度从25℃升到200℃时 所需吸收的热。
∴ ΔV≈Vg
既 W= - P饱Vg= -nRT

三、化学过程的体积功 T、P一定时，
可逆反应 aA + bB € gG + hH
气相化学反应 W=-P外∫dV =- PΔV = -Δn（g）RT
复相化学反应 W= -Δn（g）RT （固体、液体的体积

热力学第一定律ppt

热力学第一定律ppt

热力学第一定律ppt引言热力学第一定律是热力学中的基本定律之一。

它表明了能量的守恒原理，也被称为能量守恒定律。

热力学第一定律对于理解能量转化和能量守恒的过程至关重要，应用广泛。

热力学第一定律的表述热力学第一定律可以用如下方式表述：在孤立系统中，能量的增量等于对外界做功和系统热量的和。

这个表述可以用以下数学公式表示：ΔE = Q - W其中，ΔE表示能量的增量，Q表示系统吸收的热量，W表示系统对外做功。

能量转化示意图为了更好地理解热力学第一定律，我们可以通过一个能量转化示意图来说明。

能量转化示意图能量转化示意图在这个示意图中，输入的能量被系统吸收，一部分能量被转化为系统内能的增加（热量），一部分能量被系统用于对外做功。

根据热力学第一定律，系统吸收的热量和对外做的功加起来等于能量的增量。

热力学第一定律的应用热力学第一定律在工程和科学研究中有着广泛的应用。

以下是一些具体的应用：热力学循环分析热力学第一定律用于分析各种热力学循环，如卡诺循环和热力学循环。

通过应用热力学第一定律，我们可以确定循环中的能量转化效率、功率输出等参数。

能量守恒分析热力学第一定律可以应用于能量守恒的分析，例如分析能源系统中的能量损失和能量转化过程。

通过分析系统的能量转化过程，我们可以找出能量损失的原因，并采取措施来提高能源利用效率。

温度变化分析热力学第一定律可以用来分析物质的温度变化。

根据热力学第一定律，物质的内能增加会导致温度升高，而内能减少则会导致温度降低。

因此，可以通过热力学第一定律来研究物质的显热效应和隐热效应。

结论热力学第一定律是热力学中的基本定律之一，它表明了能量的守恒原理。

通过应用热力学第一定律，我们可以分析能量的转化过程，研究能源系统的能量损失和能量转化效率，并进一步提高能源利用效率。

热力学第一定律在工程和科学研究中有着广泛的应用，对于理解能量转化和能量守恒的过程起到了重要的作用。

第二章 热力学第一定律

第二章 热力学第一定律

§2-5 理想气体内能 热容和焓
一、理想气体的内能 焦耳定律 自由膨胀过程 证明：理想气体内能仅是状 态的函数，与体积无关，称 为焦耳定律
A
C
B
焦耳实验(1845年) 理想气体
U U (T )
满足pV=νRT关系；满足道尔顿分压定律； 满足阿伏加德罗定律；满足焦耳定律U
宏观特性
U (T )
1 dU CV ,m v dT
CP , m 1 dH v dT
思考题 一、试指出以下提法是否正确？如有错误、指出误区所在． 1.“高温物体所含热量多；低温物体所合热量少” 2.“同一物体温度越高所含热量越多”． 热量不是状态函数，与过程有关 二、试指出以下不同用语申的‘热”指的是哪个概念．
P
2、理想气体定容热容量及内能
热力学第一定律
dQ dU dA dU PdV dU
dV 0
dQ dU CV dT dT
U 2 U1 CV dT
T1
T2
3、理想气体定压热容量及焓 焓
H U pV U (T ) vRT
dH dU pdV
第二章
热力学第一定律
热力学系统的过程 功
内能 热量 焦耳热功当量实验
热力学第一定律及应用 理想气体内能、热容和焓 循环过程 技术上的循环过程
§2.1
一、热力学过程
热力学系统的过程
原平衡态
p
( P0 ,V0 )
一系列
非平衡态
( P ,V1 ) 1
新平衡态
p-V图 V 问题：离开了原平衡态， 能不能回到一个新平衡态
(I)“摩擦生热”； (2)“热功当最”
(3)“这盆水太热” 三、热力学系统的内能是状态的单值函数，对此作如下理解是否 正确? 1.一定量的某种气体处于一定状态，就具有一定的内能． 2.此内能是可以直接测定的． 3.此内能只有一个数值．

工程热力学 第二章 热力学第一定律

工程热力学 第二章 热力学第一定律

wt

1 2
cf22
cf21
gz2
z1 ws
(2-11)
将轴功的表达式代入上式，即有：
2
1 d ( pv)
2
2
1 pdv 1 vdp
wt 12 pdv p2v2 p1v1 12 vdp (2-11a)
由上式可知，准静态过程的 技术功的大小可用过程线左边的 面积来表示。
准静态 pdv d( pv) wt
wt pdv d( pv) pdv ( pdv vdp) vdp
wt vdp wt vdp
准静态
q du pdv
q dh vdp
热一律解析式之一 热一律解析式之二
技术功在示功图上的表示
q12 (u2 u1) w12
Q dU pdV (2-4)
2
Q12
(U2
U1)
pdV
1
(2-4a)
q du pdv (2-4b)
2
q12
(u2 u1)
pdv
1
(2-4c)
2-3 开口系统能量方程 Energy balance for open system
式中各项的正负号规定为：系统吸热为正，放热为负； 系统对外作功为正，外界对系统作功为负。
上式既适用于准静态过程，也适用于非准静态过程。
对于无耗散的准静态过程， w pdv
因此上述诸式可写为：
Q dU W
Q12 (U2 U1) W12
对1kg工质，有：
q du w
所以有：
h1 h2

1 2

热工流体第二章 热力学第一定律

热工流体第二章 热力学第一定律

第二章 热力学第一定律第一节 第一定律的实质及热力学能和总能能量守恒与转换定律是自然界的基本规律之一，它指出：自然界中的一切物质都具有能量，能量不可能被创造，也不能被消灭；但能量可以从一种形态转变为另一种形态，且在能量的转化过程中能量总量不变。

热力学第一定律是能量守恒与转换定律在热现象中的应用。

它确定了热力过程中热力系统与外界进行能量交换时，各种形态能量数量上的守恒关系。

一、热力学能热力学能是与物质内部粒子的微观运动和粒子的空间位置有关的能量。

它包括分子移动、转动、粒子震动运动的内动能和分子间由于相互作用力的存在而具有的内位能，故又称内能。

内动能取决于分子热运动，是温度的函数，而内位能取决于分子间的距离，是比体积的函数，即u = f ( T, v )二、总能除热力学能外，工质的总能量还包括工质在参考坐标系中作为一个整体，因有宏观运动速度而具有动能、因有不同高度而具有位能。

前一种能量称之为内部储存能，后两种能量则称之为外部储存能。

我们把内部储存能和外部储存能的总和，即热力学能与宏观运动动能和位能的总和，叫做工质的总储存能，简称总能。

即p k E U E E =++ （2-1）E---总能； U---热力学能； E k ---宏观动能； E p ---宏观位能。

第二节 第一定律的基本能量方程及工质的焓一、焓在有关热力计算总时常有U+pV 出现，为了简化公式和计算，把它定义为焓，用符号H 表示，即H=U+pV （2-2）1kg工质的焓值称为比焓，用h表示，即h=u+pv （2-3）焓的单位是J，比焓的单位是J/kg。

焓是一个状态参数，在任一平衡状态下，u、p和v都有一定得值，因而焓h也有一定的值，而与达到这一状态的路径无关。

当1kg工质通过一定的界面流入热力系统时，储存于它内部的热力学能当然随着也进入到系统中，同时还把从外部功源获得的推动功pv带进了系统。

因此系统中因引进1kg工质而获得的总能量是热力学能与推动功之和（u+pv），即比焓。

02第二章 热一律2-1热力学第一定律的实质及表达式

02第二章 热一律2-1热力学第一定律的实质及表达式

吸热膨胀作功（参看图2-3c） 吸热膨胀作功 外界供给热量 –Q 膨胀功 –W 热力学能 –U2
排气过程中（参看图2-3d） 排气过程中 外界消耗排气功 外界获得推动功 排气后（参看图2-3a） 排气后 质量 m = 0 总能量 E2 = 0
开口系在一个工作周期中的能量进出情况
Q=Q ∆E = 0
1 2 2 w = ( p2 v2 − p1v1 ) + (c2 − c1 ) + g ( z 2 − z1 ) + wsh 2
（2-16）
总功（Wtot ）、膨胀功（W ）、技术功（ W t ）和轴功 （W sh ）之间的区别和内在联系 膨胀功、技术功、轴功孰大孰小取决于 ( p 2 v2 − p1v1 ) 1 2 2 (c2 − c1 ) 、 g ( z 2 − z1 ) 的大小和正负。
二、热力学第一定律表达式
1、一般热力系能量方程
- 热力学第一定律基本表达式
热力系总能量(total stored energy of system)为E（图2-1a）。它是 热力学能（U）、宏观动能（EK）和重力位能（EP）的总和： 热力学能，内部储存能 热力学能，
E =U+Ek +Ep
宏观动能 总能 宏ቤተ መጻሕፍቲ ባይዱ位能 外部储存能
e =u+ek +ep
根据质量守恒定律可知：热力系质量的变化等于流进和流出 质量的差：
dm = δm1 − δm2
根据热力学第一定律可知：
热力系输出的能量的总和= 加入热力系的能量的总和 - 热力系输出的能量的总和=热力系总能量的增量
（δQ + e1δm1） (δW总 + e2δm2 ) = ( E + dE ) − E −

热力学第一定律PPT课件

U = f ( T ) ——这称为Joule定律
原因：
T不变，U ＝ 0
理想g分子间无相互作用力。无分子间相互作用的 势能，U只是分子的平动、转动、分子内部各原子间的
振动、电子的运动、核的运动的能量之和，这些能量均
取决于T。
注意：
实际g分子间有相互作用力。U与T，V都有关。
7
§2.3 恒容热、恒压热及焓
已知：C p,m ( Ar(g) ) . J .mol-.K -
C p,m Cu(s) .J .mol-.K -
并假设其不随温度变化
始态
4mol Ar(g) 2mol Cu(s) T1 = 273.15K V1＝0.1m3
dV=0
求：Q、W、 U及H
末态
pamb 0 W 0
过程中水温未变：Q ＝0
U ＝ 0
5
§2.2 热力学第一定律
对于单相、均匀的单组成系统，若n一定，则热力 学能可表示为 p, V, T 中的任意两个变量的函数。
设 U f (T ,V ) dU U dV U dT
V T
如：在恒T、恒P, W = 0的条件下 CO(g) 的生成反应：
C 石墨 O2 g CO2 g 1 Qp可由实验
CO
g


1 2
O2

g


CO2

g

3
直接测定
C
石墨


1 2
O2

g


CO
g

(2) Qp不能直接测定
反应(1 ) - (3)＝(2) H2 = H1 －H3

第二章 热力学第一定律

系统能量的增加： 系统能量的增加：∆ECV＝0
进入系统的能量－离开系统的能量＝系统能量的增加 （2－9） 进入系统的能量－离开系统的能量＝ － ）
1 2 Q = m2 (u2 + cf 2 + gz2 ) + m2 p2 v2 2 1 2 − m1 (u1 + cf 1 + gz1 ) − m1 p1v1 + Wi 2
1 2 wt = (cf 2 − cf21 ) + g ( z 2 − z1 ) + wi 2
比较式（2－10b)和（2－16） 比较式（ － 和 － ）
(2 − 19)

q = ∆u + w q = ∆h + wt = ∆u + ∆( pv) + wt 1 2 w = ∆( pv) + wt = ∆( pv) + ∆cf + g∆z + wi 2
由于m 由于 1=m2=m, 整理上式得
1 2 Q = m(u2 + p2 v2 + cf 2 + gz2 ) 2 1 2 − m(u1 + p1v1 + cf 1 + gz1 ) + Wi 2 令 H = U + pV 代入上式得
1 Q = ∆H + m∆cf2 + mg∆z + Wi 2 1 2 δQ = dH + mdcf + mgdz + δWi 2
m1 = m2 = m
∆ECV = 0
稳定系统的能量分析： 稳定系统的能量分析： 进入系统的能量： 进入系统的能量：
1 2 Q + E1 + p1V1 = Q + m1 (u1 + cf 1 + gz1 ) + m1 p1v1 2 离开系统的能量： 离开系统的能量： 1 2 E2 + p2V2 + Wi = m2 (u 2 + cf 2 + gz 2 ) + m2 p2 v2 + Wi 2

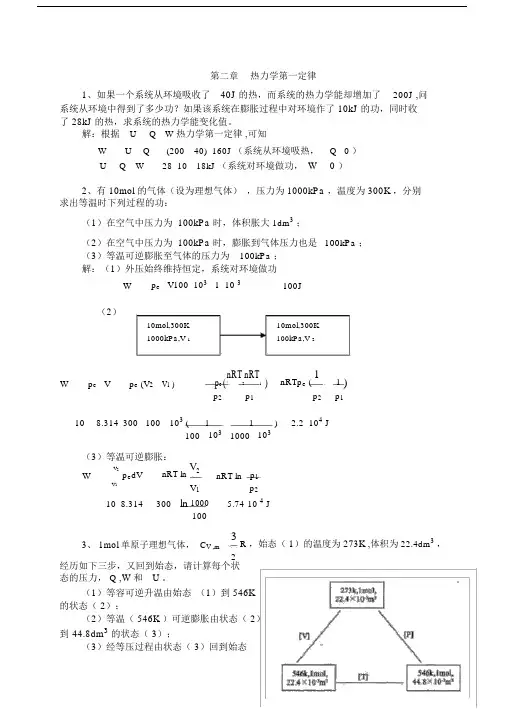
(完整版)第二章热力学第一定律.doc

第二章热力学第一定律1、如果一个系统从环境吸收了40J 的热，而系统的热力学能却增加了200J ,问系统从环境中得到了多少功？如果该系统在膨胀过程中对环境作了 10kJ 的功，同时收了 28kJ 的热，求系统的热力学能变化值。

解：根据U Q W 热力学第一定律,可知W U Q (200 40) 160J （系统从环境吸热，Q 0 ）U Q W 28 10 18kJ （系统对环境做功，W 0 ）2、有 10mol 的气体（设为理想气体），压力为 1000kPa ，温度为 300K ，分别求出等温时下列过程的功：（1）在空气中压力为 100kPa 时，体积胀大1dm3；（2）在空气中压力为 100kPa 时，膨胀到气体压力也是100kPa ；（3）等温可逆膨胀至气体的压力为100kPa ；解：（1）外压始终维持恒定，系统对环境做功W p e V100 103 1 10 3 100J（2）10mol,300K10mol,300K1000kPa,V 1100kPa,V 2W p e V p e (V2 V1 ) p e(nRT2nRT1) nRTp e (11 )p2 p1 p2 p110 8.314 300 100 103 ( 1 1103 ) 2.2 104 J100 103 1000（3）等温可逆膨胀：V2p e dV nRT ln V2 nRT ln p1WV1 V1 p210 8.314 300 ln 1000 5.74 10 4 J1003、 1mol 单原子理想气体，C V ,m 3R ，始态（1）的温度为273K ,体积为 22.4dm3，2经历如下三步，又回到始态，请计算每个状态的压力， Q ,W和U 。

（1）等容可逆升温由始态（1）到 546K 的状态（ 2）；（2）等温（ 546K ）可逆膨胀由状态（ 2）到44.8dm3的状态（ 3）；（3）经等压过程由状态（ 3）回到始态（ 1）；解：（1）等容可逆升温过程：W P e V 0UQ WQ VT 2 nC V ,m dT 138.314 546 273 3404.58 JT 12（2）等温可逆膨胀过程：U 0WnRT lnV 21 8.314 546ln 44.83146.50JV 122.4Q W 3146.50J（3）等压过程 :WP e VnRT V 1 V 2 1 8.314 273 22.4 44.8 10 3 2269.72 JV 1 22.4 10 3Q pH T 2nC P ,m dT n 3 R 273 546 5 8.314 273 5674.31J T 1 R 12 2UQ W 5674.31 2269.72 3404.59 J4、在 291K 和 100kPa 下， 1molZn (s) 溶于足量稀盐酸中， 置换出 1molH 2 ( g) ，并放热 152kJ 。

第二章 热力学第一定律

理想气体
内能
u = u(T, v)
u = u(T )
内能U的说明： 内能 的说明： 的说明
内能是状态量 • 内能是状态量 • U : [ kJ ] u : [kJ/kg] 内能总以变化量出现 内能零点人为定 • 内能总以变化量出现 ∆u，内能零点人为定
§2-2 热力学第一定律的实质
能量守恒与转化定律（ 能量守恒与转化定律（conversation of energy） ） 热一律的实质 能量守恒 转换定律 实质： 守恒及 热一律的实质：能量守恒及转换定律 热过程中的应用 在热过程中的应用
可逆过程容 可逆过程容 积变化功： 积变化功： 闭口系统能 量方程： 量方程：
δw = pdv δq = du + δw
δq = du + pdv q = ∆ u + ∫ pdv
注意公式应用条件
例2 - 1 如图所示，闭口系内的一定量气体由状态1 如图所示 ， 闭口系内的一定量气体由状态 1 经 1a2 变化至状态2 吸热70kJ， 同时对外做功25kJ，， 70kJ 25kJ 变化至状态 2 ， 吸热 70kJ ， 同时对外做功 25kJ ，， 试问： 工质若由1 变化到2 试问：（1）工质若由1经1b2变化到2时，吸热为 90kJ 则对外做功是多少？ kJ， 90kJ ， 则对外做功是多少 ？ （ 2 ） 若外界对气体 做功30kJ， 迫使它从状态2 30kJ 返回到状态1 做功 30kJ ， 迫使它从状态 2 经 2c1 返回到状态 1 ， 则此返回过程是吸热过程还是放热过程？ 则此返回过程是吸热过程还是放热过程？其值为 多少？ 多少？
E = U + Ek + Ep e = u + ek + ep
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
积V变化的函数关系式p=p(V)，然后代入公式， 就可以求出一过程所作的功； 4、我们讨论的都是体积功； 5、功还可以利用p-V图求出作功的大小，在图 中曲线下方所围成的面积就是功的大小，功的 正负由曲线上的箭头来判断。
例题：1mol理想气体，初态的压强、体积和温度 分别为p1、V1和T1。若体系经历一个压强与体积满 足关系p=aV的过程，其中a为常数，试求： （1）用p1、T1和R来表示常数a； （2）若系统经历此过程体积扩大一倍，则系统的 温度T为多少？在此过程中对外所做的功为多少？
§2.2 功
一、功是力学相互作用下的能量转移
力学相互作用：将力学平衡条件被破坏时所产生的对系统 状态的影响。
在力学相互作用过程中系统和外界之间转移的能量就是功。
热力学认为力是一种广义力，所以功也是广义功。
注意：
1）、只有在系统状态变化过程中才有能量转移。
2）、只有在广义力（如压强、电动势等）作用下 产生了广义位移（如体积变化、电量迁移等）后 才作了功。 3）、在非准静态过程中很难计算系统对外作的功。
三、准静态过程
如果一个热力学系统过程在始末两平衡态 之间所经历的之中间状态，可以近似当作 平衡态，则此过程为准静态过程。
注意
•准静态过程只有在进行的“无限缓慢” 的条件下才可能实现
•对于实际过程则要求系统状态发生变化的 特征时间远远大于弛豫时间才可近似看作 准静态过程。
准静态过程例子
无摩擦准静态过程，其特点是没有摩擦力， 外界在准静态过程中对系统的作用力，可以用 系统本身的状态参量来表示。
当热力学系统的状态随时
间变化时，我们就说系统 在经历一个热力学过程， 简称过程。
推进活塞压缩汽缸内的 气体时，气体的体积、 密度、温度或压强都将 变化
二、非静态过程
1、弛豫时间：系统由非平衡态到达平衡态所 需要的时间称为弛豫时间。用τ表示
2、弛豫过程：由非平衡态到达平衡态的过程 称为弛豫过程。
3、非静态过程：在热力学过程的发生时，系 统往往由一个平衡状态经过一系列状态变化 后到达另一平衡态。如果中间状态为非平衡 态，则此过程称非静态过程。 作为中间态的非平衡态通常不能用状态参量 来描述。
4T1
No
ImAagVe2 pdV 2V1 aVdVIamVa2 2gV1e
V1
V1
2
V1
a 2
[例] 右图活塞与汽缸无摩擦，当气体作准静态
压缩或膨胀时，外界的压强Pe必等于此时气体的
压强P，否则系统在有限压
dx
差作用下，将失去平衡，
称为非静态过程。若有摩
擦力存在，虽然也可使过 S P
程进行的“无限缓慢”，
Pe
但Pe≠P。
显然作为准静态过程中间状 态的平衡态，具有确定的状 态参量值，对于简单系统可 用P—V图上的一点来表示 这个平衡态。系统的准静态 变化过程可用P—V图上的 一条曲线表示，称之为过程 曲线（右图）。
四、功是过程量
注意
三种过程的初、末状态相同， 但所作的功不同；说明功不仅 与初、末状态有关，而且与变 化的路径也有关，证明它不是 状态的函数，而是过程量。

五、理想气体在几种等值过程中功的计算 等温过程：
等压过程： 等体过程：
六、其它形式的功 1、拉伸弹簧棒所作的功
A
F
F
l0 l0+dl
2、表面张力功
x
dx
L
A
dA 2ldx dS
F
σ是表面张力系数
3、可逆电池所作的功
dA dq
a G
Cu
CuSO4
b
E
Zn 可 逆 电 池
ZnSO4
4、功的一般表达式
dWi Yidxi
x是 广义坐标，它是广延量，广 延量的特征是：若系统在相同情况下 质量扩大一倍，则广延量也扩大一倍。 如：体积，面积，电极化强度等。
准静态过程是一种理想的极 限，但作为热力学的基础， 我们要首先着重讨论它。
外界对系统的作用使系统的状态发生了变化， 这种相互作用的情况用力的情况来反映是不 方便的，有的时候甚至是不可能的，但是作 用的结果是使系统的能量发生了改变，作为 能量变化的量度是功，作为能量变化的主要 形式之一是热量的交换，因此，外界的作用 就是功和热的转移，从而使系统的状态发生 改变，为此，我们以后就以功和热为两条主 要线索来反映系统和外界的相互作用了。
Y是广义力，它是强度量，强度量 的特征是：当系统在相同情况下质量扩 大一倍时，强度量不变。如：压强，表 面张力，电场强度等。
七、对功的计算公式，有几点说明：
1、功不但与系统的初、末状态有关，而且与过 程有关，即功是过程量；
2、只适用于无摩擦的准静态过程； 3、用公式来计算功时，必须先找到压强p随体
第二章 热力学第一定律
§2.1 §2.2 §2.3 §2.4 §2.5 §2.6
§2.7 §2.8
热力学系统的过程 功 内能 热量 焦耳热功当量实验 热力学第一定律 理想气体的内能、热容和焓 热力学第一定律对理想气体 几种典型过程的应用 循环过程 技术上的循环实例
§2.1 热力学系统的过程
一、热力学过程
解：（1）由理想气体的状态方程，得
p1V1 RT1，而 p1 aV1 aV1V1 RT1，即 aRV12T1 Rp12T1
（2）初态： p1，V1，T1
p1V1 RT1
末态： p2， V2V1， T2 p22V1 RT2
而 p2aV 2R V121T2V12V R11T
T2No2pR2V1
22V R1T1V1 R
4）、功有正负之分。
二、功的表达式（体积功）
1、气体对外界所作的元功为： 所作的总功为：
dA pSdx pdV
A V2 pdV V1
2、外界对气体所作的功为：
A V2 pdV V1
三、功的图示
注意
当dV>0，即气体体积膨胀时，
则dA>0，作正功，系统对外界作功； 当dV<0，即气体体积压缩时， 则dA<0，作负功，外界对系统作功。
第二章热力学第一定律演 示文稿
教学基本要求
一 掌握内能、功和热量等概念 . 理解准静 态过程 .
二 掌握热力学第一定律，能分析、计算理 想气体在等体、等压、等温和绝热过程中的功、 热量和内能的改变量 .
三 理解循环的意义和循环过程中的能量转 换关系，会计算卡诺循环和其他简单循环的效率 .
四 了解可逆过程和不可逆过程，了解热力 学第二定律和熵增加原理 .