第二章-热力学第一定律
- 格式：docx
- 大小：54.27 KB
- 文档页数：8
下载文档原格式
合集下载
第二章 热力学第一定律
T (B, ,T)
£K r Hm (T)
标准摩尔燃烧焓[变]的定义 在温度 T 物质 B 完全氧化( T)表示 叫标准摩尔燃烧焓 g H2O(l)的 T)计算
£K r Hm £K cHm £K r Hm B
-
)成相同温度下指定产物时的标准摩尔焓[变] 用
£K cHm
(B
指定产物 CO2 由
£K c Hm
物理化学学习指导
第二章 热力学第一定律
第二章 热力学第一定律
一. 基本概念及公式
1 热力学基本概念
(1)系统和环境 系统——热力学研究的对象(是大量分子 外的周围部分存在边界 环境——与系统通过物理界面(或假想的界面)相隔开并与系统密切相关的周围部分 根据系统与环境之间发生物质的质量与能量的传递情况 系统分为三类: 原子 离子等物质微粒组成的宏观集合体) 系统与系统之
H = Qp 适用于真实气体 理想气体 液体
T2 T1
∆H = ∫ nC p ,m dT
T1
T2
固体定压过程 理想气体任意 p
V
T 变化过程
∆U = ∫ nCV ,m dT = nC v ,m (T2 − T1 ) ∆H = ∫ nC p ,m dT = nC p ,m (T2 − T1 )
T1 T2
体积功 功有多种形式 通常涉及的是体积功 它是系统发生体积变化时的功 定义为
δW = − p su dV
式中 psu 为环境的压力
W = ∑ δW = − ∫ p su dV
V2 V1
对恒外压过程
psu = 常数
W = − p su (V2 − V1 ) W = − ∫ pdV
V1 V2
对可逆过程 因 p =psu
第二章热力学第一定律
敞开系统 系 统
所研究的 物质对象
系统与环境
物质进出 能量得失 √ √
封闭系统 隔离系统
√
状态及状态函数
系统有p, V, T, 组成, 内能等等宏观性质, 系统内的每个粒子 又有结构, 运动情况和粒子间相互作用等微观性质. 系统的宏观 性质有些是各粒子微观性质的某种平均作用, 如温度是分子热 运动的平均强度; 有些则是粒子微观性质的总体表现, 如压力是 分子运动碰撞容器壁面时对单位面积壁面的总垂直力.
状态及状态函数
系统的状态 是系统所有宏观性质的综合表现. 具有单值对应的函数关系 (a) 系统所有的性质一定, 状态就一定; (实际上当系统中物质量及组成, 温度, 压力(或体积) 一定时, 状态便可确定) (b) 状态一定, 系统所有的性质均一定. 因此, 宏观性质又称为状态函数 状态函数的基本性质——状态函数法的基础. • 其微小变化值可用数学上的全微分表示，如dT, dp, dV… • 其增量只与系统的始态和终态有关, 与具体变化途径无关
系统的宏观性质简称性质, 有的可以测量, 有的不可以测量. 性质可分为如下两大类:
系统的性质
{ 强度性质 无空间上的加和性: T,
T p T p
广延性质 有空间上的加和性: n, V ,U, H ,S ,G …
p ,Vm , Um …
nL VL UL SL nR VR UR SR
两者的关系：广延性质的 摩尔量是(准)强度性质， 如:摩尔体积 Vm 等.
{p
su
}
W
p始
一粒粒取走砂粒 (剩 余 砂 粒 相 当 前 述 一个重物)
V终
p始
V始
所研究的 物质对象
系统与环境
物质进出 能量得失 √ √
封闭系统 隔离系统
√
状态及状态函数
系统有p, V, T, 组成, 内能等等宏观性质, 系统内的每个粒子 又有结构, 运动情况和粒子间相互作用等微观性质. 系统的宏观 性质有些是各粒子微观性质的某种平均作用, 如温度是分子热 运动的平均强度; 有些则是粒子微观性质的总体表现, 如压力是 分子运动碰撞容器壁面时对单位面积壁面的总垂直力.
状态及状态函数
系统的状态 是系统所有宏观性质的综合表现. 具有单值对应的函数关系 (a) 系统所有的性质一定, 状态就一定; (实际上当系统中物质量及组成, 温度, 压力(或体积) 一定时, 状态便可确定) (b) 状态一定, 系统所有的性质均一定. 因此, 宏观性质又称为状态函数 状态函数的基本性质——状态函数法的基础. • 其微小变化值可用数学上的全微分表示，如dT, dp, dV… • 其增量只与系统的始态和终态有关, 与具体变化途径无关
系统的宏观性质简称性质, 有的可以测量, 有的不可以测量. 性质可分为如下两大类:
系统的性质
{ 强度性质 无空间上的加和性: T,
T p T p
广延性质 有空间上的加和性: n, V ,U, H ,S ,G …
p ,Vm , Um …
nL VL UL SL nR VR UR SR
两者的关系：广延性质的 摩尔量是(准)强度性质， 如:摩尔体积 Vm 等.
{p
su
}
W
p始
一粒粒取走砂粒 (剩 余 砂 粒 相 当 前 述 一个重物)
V终
p始
V始
第2章热力学第一定律
技术功：技术上可以利用的功
1 2 wt c gz wi 2
q u w
wt w pv w p2 v2 p1v1
可逆过程
wt pdv p1v1 p2v2 pdv d pv vdp
2 2 2 2 1 1 1 1
第二章 热力学第一定律
本章要求
理解热力学第一定律的实质—能量守恒定律 掌握流动功,轴功及技术功的概念 注意热力学能，焓的引入及定义
掌握热力学第一定律能量方程的基本表达式 及稳定流动能量方程
本章学习流程
热力学第一定律的提出
热力系能量的组成
能量之间的传递和转化 ＋ 焓
闭口系能量方程 ＋ 开口系能量方程 （第一定律数学表达式）
热力学能只取决于热力系内部的状态,且具有 可加性,是一个具有广延性质的状态参数
2
1
du u 2 u1
du 0
2u 2u Tv vT
u u du dT dv T v v T
二．外储存能
工质在参考坐标系中作为一个整体，因有宏观 速度而具有动能，因有高度差而具有位能
热力学能：是指储存于热力系内部的能量． 用U表示，单位是J或 kJ，单位质量工质的热力 学能称为比热力学能，用u表示，单位是J/kg或 kJ/Kg
热力学能是工质的状态参数，完全取决于工 质的初态和终态，与过程的途径无关
热力学能为两个独立状态参数的函数： u=f(T,v)或u=f(T,p)或u=f(p,v)
能量方程式的应用
确定研究对象—选好热力系统
写出所研究热力系对应的能量方程
针对具体问题,分析系统与外界的相互作用, 作出某些假设和简化,使方程简单明了 求解简化后的方程,解出未知量
第二章 热力学第一定律
§2-5 理想气体内能 热容和焓
一、理想气体的内能 焦耳定律 自由膨胀过程 证明：理想气体内能仅是状 态的函数，与体积无关，称 为焦耳定律
A
C
B
焦耳实验(1845年) 理想气体
U U (T )
满足pV=νRT关系；满足道尔顿分压定律； 满足阿伏加德罗定律；满足焦耳定律U
宏观特性
U (T )
1 dU CV ,m v dT
CP , m 1 dH v dT
思考题 一、试指出以下提法是否正确？如有错误、指出误区所在． 1.“高温物体所含热量多；低温物体所合热量少” 2.“同一物体温度越高所含热量越多”． 热量不是状态函数，与过程有关 二、试指出以下不同用语申的‘热”指的是哪个概念．
P
2、理想气体定容热容量及内能
热力学第一定律
dQ dU dA dU PdV dU
dV 0
dQ dU CV dT dT
U 2 U1 CV dT
T1
T2
3、理想气体定压热容量及焓 焓
H U pV U (T ) vRT
dH dU pdV
第二章
热力学第一定律
热力学系统的过程 功
内能 热量 焦耳热功当量实验
热力学第一定律及应用 理想气体内能、热容和焓 循环过程 技术上的循环过程
§2.1
一、热力学过程
热力学系统的过程
原平衡态
p
( P0 ,V0 )
一系列
非平衡态
( P ,V1 ) 1
新平衡态
p-V图 V 问题：离开了原平衡态， 能不能回到一个新平衡态
(I)“摩擦生热”； (2)“热功当最”
(3)“这盆水太热” 三、热力学系统的内能是状态的单值函数，对此作如下理解是否 正确? 1.一定量的某种气体处于一定状态，就具有一定的内能． 2.此内能是可以直接测定的． 3.此内能只有一个数值．
工程热力学 第二章 热力学第一定律
wt
1 2
cf22
cf21
gz2
z1 ws
(2-11)
将轴功的表达式代入上式，即有：
2
1 d ( pv)
2
2
1 pdv 1 vdp
wt 12 pdv p2v2 p1v1 12 vdp (2-11a)
由上式可知，准静态过程的 技术功的大小可用过程线左边的 面积来表示。
准静态 pdv d( pv) wt
wt pdv d( pv) pdv ( pdv vdp) vdp
wt vdp wt vdp
准静态
q du pdv
q dh vdp
热一律解析式之一 热一律解析式之二
技术功在示功图上的表示
q12 (u2 u1) w12
Q dU pdV (2-4)
2
Q12
(U2
U1)
pdV
1
(2-4a)
q du pdv (2-4b)
2
q12
(u2 u1)
pdv
1
(2-4c)
2-3 开口系统能量方程 Energy balance for open system
式中各项的正负号规定为：系统吸热为正，放热为负； 系统对外作功为正，外界对系统作功为负。
上式既适用于准静态过程，也适用于非准静态过程。
对于无耗散的准静态过程， w pdv
因此上述诸式可写为：
Q dU W
Q12 (U2 U1) W12
对1kg工质，有：
q du w
所以有：
h1 h2
1 2
热工流体第二章 热力学第一定律
第二章 热力学第一定律第一节 第一定律的实质及热力学能和总能能量守恒与转换定律是自然界的基本规律之一，它指出：自然界中的一切物质都具有能量，能量不可能被创造，也不能被消灭；但能量可以从一种形态转变为另一种形态，且在能量的转化过程中能量总量不变。
热力学第一定律是能量守恒与转换定律在热现象中的应用。
它确定了热力过程中热力系统与外界进行能量交换时，各种形态能量数量上的守恒关系。
一、热力学能热力学能是与物质内部粒子的微观运动和粒子的空间位置有关的能量。
它包括分子移动、转动、粒子震动运动的内动能和分子间由于相互作用力的存在而具有的内位能，故又称内能。
内动能取决于分子热运动，是温度的函数，而内位能取决于分子间的距离，是比体积的函数，即u = f ( T, v )二、总能除热力学能外，工质的总能量还包括工质在参考坐标系中作为一个整体，因有宏观运动速度而具有动能、因有不同高度而具有位能。
前一种能量称之为内部储存能，后两种能量则称之为外部储存能。
我们把内部储存能和外部储存能的总和，即热力学能与宏观运动动能和位能的总和，叫做工质的总储存能，简称总能。
即p k E U E E =++ （2-1）E---总能； U---热力学能； E k ---宏观动能； E p ---宏观位能。
第二节 第一定律的基本能量方程及工质的焓一、焓在有关热力计算总时常有U+pV 出现，为了简化公式和计算，把它定义为焓，用符号H 表示，即H=U+pV （2-2）1kg工质的焓值称为比焓，用h表示，即h=u+pv （2-3）焓的单位是J，比焓的单位是J/kg。
焓是一个状态参数，在任一平衡状态下，u、p和v都有一定得值，因而焓h也有一定的值，而与达到这一状态的路径无关。
当1kg工质通过一定的界面流入热力系统时，储存于它内部的热力学能当然随着也进入到系统中，同时还把从外部功源获得的推动功pv带进了系统。
因此系统中因引进1kg工质而获得的总能量是热力学能与推动功之和（u+pv），即比焓。
第二章 热力学第一定律
15
§2-4焓
焓: 比焓定义为： ∴ 焓=
H U PV
（2-5） （2-5a）
h u pv
内能 +推动功
从2－5式可知，焓是一个状态参数，它可以表示成 另外两个独立状态参数的函数，即
h f p, v
（2-6）
h f T , v
h f p, T
（2-6a）
1、 2、 3、
m out m in m
Q Const
1 2 cin 2 gz
in
W
net
W net Const W s
轴功
Q gz out
4、
每截面状态不变
dEC ,V / 0
1 2 cout 2
m out u out
稳定流动能量方程的推导
稳定流动条件
Q0
T
W 0
电 冰 箱
门窗紧闭房间用空调降温
以房间为系统 闭口系能量方程
闭口系
Q0
Q W
W 0
T
Q
空 调
例自由膨胀
如图， 抽去隔板，求
U
解：取气体为热力系 —闭口系？开口系？
Q U W
Q0
W ?0
U 0
强调：功是通过边界传递的能量。 例A4302661
气缸活塞抬升做功
§2-5热力学第一定律的基本能量方程式
1.：系统能量平衡方程式： 进入能量-离开能量=储存能变化 2.闭口系能量平衡方程式: （2-9）
Q W U 或
Q U W
（2-10）
意义：(2-10）式也被称为热力学第一定律的解析式，表 明加给工质的热量一部分用于增加工质的热力学能，储存 于工质内部，余下的一部分以作功的方式传递至外界 3.微元过程:
第二章 热力学第一定律
第二章 热力学第一定律
热力学是自然科学中建立最早的学科之一，是 研究不同形式能量转化的科学。
热力学第一、第二定律于19世纪中叶被提出;
热力学定律是经验定律，不能用数学证明; 热力学理论是通过逻辑推理＋数学运算得出的。 第一定律：能量守恒，解决过程的能量衡算问题 （功、热、热力学能的计算） 第二定律：过程进行的方向和限度的判据 第三定律：解决物质熵的计算
Ｕ =Ｑ ＋ Ｗ
Ｕ 系统热力学能（内能）的增量；
Q 系统与环境交换的热，得热为＋，失热为－ W 系统与环境交换的功，得功为＋，失功为－
即：封闭系统中内能的增加，等于它所吸收的热 加上它所得到的功 若系统发生微小变化，有： dU = Q +W 热力学第一定律的其它说法： 要制造一种既产生功又不需供给相当能量 的机器（第一类永动机）是不可能的。
CV ,m C p ,m
CV,m和Cp,m 的关系
C p ,m CV ,m H m U m U m pVm U m T T T p T V V p Vm U m p T T p V
在任何隔离系统中，所储存的总能量不变。
2. 热力学能U的意义
U是系统内部所储存的总能量 系统内部分子的动能 包括 分子相互间作用的位能 分子内部原子、电子、及核的能量 U 具有加和性，所以是广度量。（Um是强度量） U 是状态函数 U＝ f ( T, V ) (n一定)
（具有全微分性质）
U U dU d V dT V T T V
V2
V2
V
V2 Wr nRT ln V 1
p1 nRT ln p 2
热力学是自然科学中建立最早的学科之一，是 研究不同形式能量转化的科学。
热力学第一、第二定律于19世纪中叶被提出;
热力学定律是经验定律，不能用数学证明; 热力学理论是通过逻辑推理＋数学运算得出的。 第一定律：能量守恒，解决过程的能量衡算问题 （功、热、热力学能的计算） 第二定律：过程进行的方向和限度的判据 第三定律：解决物质熵的计算
Ｕ =Ｑ ＋ Ｗ
Ｕ 系统热力学能（内能）的增量；
Q 系统与环境交换的热，得热为＋，失热为－ W 系统与环境交换的功，得功为＋，失功为－
即：封闭系统中内能的增加，等于它所吸收的热 加上它所得到的功 若系统发生微小变化，有： dU = Q +W 热力学第一定律的其它说法： 要制造一种既产生功又不需供给相当能量 的机器（第一类永动机）是不可能的。
CV ,m C p ,m
CV,m和Cp,m 的关系
C p ,m CV ,m H m U m U m pVm U m T T T p T V V p Vm U m p T T p V
在任何隔离系统中，所储存的总能量不变。
2. 热力学能U的意义
U是系统内部所储存的总能量 系统内部分子的动能 包括 分子相互间作用的位能 分子内部原子、电子、及核的能量 U 具有加和性，所以是广度量。（Um是强度量） U 是状态函数 U＝ f ( T, V ) (n一定)
（具有全微分性质）
U U dU d V dT V T T V
V2
V2
V
V2 Wr nRT ln V 1
p1 nRT ln p 2
第2章 热力学第一定律
第二章热力学第一定律First law of thermodynamics First law of thermodynamics2–1 热力学第一定律的实质2-2 热力学能（内能）和总能2-22–3 热力学第一定律基本表达式2–4 闭口系基本能量方程式252–5 开口系能量方程12–1热力学第一定律的实质一、第一定律的实质能量守恒与转换定律在热现象中的应用。
二、第一定律的表述第定律的表述热是能的一种，机械能变热能，或热能变机械能的时候，他们之间的比值是一定的。
或：热可以变为功，功也可以变为热；一定量的热消失时必定产生相应量的功；消耗一定量的功时，必出现与之相应量的热。
22–2 热力学能（内能）和总能一、热力学能(internal energy)UU chU nu k平移动能U thU k 转动动能振动动能()T f 1),(v T U U =U p —()v T f ,2二、总（储存）能(total stored energy of system)、总（储存）能(o s o ed e e gy o sys e )++热力学能，内部储存能k pk pE U E E e u e e =++=3总能外部储存能宏观动能宏观位能宏观动能与内动能的区别2–3 热力学第一定律基本表达式加入系统的能量总和－热力系统输出的能量总和= 热力系总储存能的增量δW+d EE d Eδi im e δj jm e δQd ττ+τ流入：δδi iQ m e +∑流出：δδjjW m e+∑5内部贮能的增量：d E2–4 闭口系基本能量方程式τ⎡()()21tot δδj j i i Q E e m e m W τ⎤=∆+Σ−Σ+⎣⎦∫闭口系，δ0δ0i j m m ==忽略宏观动能U k 和位能U p ，E U∆=∆δd δδd δQ U W Q U W u wu w=∆+=+=∆+=+q q 第一定律第一解析式—功的基本表达式热7讨论：δd δU W U W =∆+=+δd δQ Q q u wq u w=∆+=+1）对于可逆过程δd d Q U p V=+2）对于循环netnetδd δQ U W QW =+⇒=∫∫∫ 3）对于定量工质吸热与升温关系，还取决于W 的”“+”、“–”、数值大小。
第二章 热力学第一定律
系统能量的增加： 系统能量的增加：∆ECV＝0
进入系统的能量－离开系统的能量＝系统能量的增加 （2－9） 进入系统的能量－离开系统的能量＝ － ）
1 2 Q = m2 (u2 + cf 2 + gz2 ) + m2 p2 v2 2 1 2 − m1 (u1 + cf 1 + gz1 ) − m1 p1v1 + Wi 2
1 2 wt = (cf 2 − cf21 ) + g ( z 2 − z1 ) + wi 2
比较式（2－10b)和（2－16） 比较式（ － 和 － ）
(2 − 19)
q = ∆u + w q = ∆h + wt = ∆u + ∆( pv) + wt 1 2 w = ∆( pv) + wt = ∆( pv) + ∆cf + g∆z + wi 2
由于m 由于 1=m2=m, 整理上式得
1 2 Q = m(u2 + p2 v2 + cf 2 + gz2 ) 2 1 2 − m(u1 + p1v1 + cf 1 + gz1 ) + Wi 2 令 H = U + pV 代入上式得
1 Q = ∆H + m∆cf2 + mg∆z + Wi 2 1 2 δQ = dH + mdcf + mgdz + δWi 2
m1 = m2 = m
∆ECV = 0
稳定系统的能量分析： 稳定系统的能量分析： 进入系统的能量： 进入系统的能量：
1 2 Q + E1 + p1V1 = Q + m1 (u1 + cf 1 + gz1 ) + m1 p1v1 2 离开系统的能量： 离开系统的能量： 1 2 E2 + p2V2 + Wi = m2 (u 2 + cf 2 + gz 2 ) + m2 p2 v2 + Wi 2
进入系统的能量－离开系统的能量＝系统能量的增加 （2－9） 进入系统的能量－离开系统的能量＝ － ）
1 2 Q = m2 (u2 + cf 2 + gz2 ) + m2 p2 v2 2 1 2 − m1 (u1 + cf 1 + gz1 ) − m1 p1v1 + Wi 2
1 2 wt = (cf 2 − cf21 ) + g ( z 2 − z1 ) + wi 2
比较式（2－10b)和（2－16） 比较式（ － 和 － ）
(2 − 19)
q = ∆u + w q = ∆h + wt = ∆u + ∆( pv) + wt 1 2 w = ∆( pv) + wt = ∆( pv) + ∆cf + g∆z + wi 2
由于m 由于 1=m2=m, 整理上式得
1 2 Q = m(u2 + p2 v2 + cf 2 + gz2 ) 2 1 2 − m(u1 + p1v1 + cf 1 + gz1 ) + Wi 2 令 H = U + pV 代入上式得
1 Q = ∆H + m∆cf2 + mg∆z + Wi 2 1 2 δQ = dH + mdcf + mgdz + δWi 2
m1 = m2 = m
∆ECV = 0
稳定系统的能量分析： 稳定系统的能量分析： 进入系统的能量： 进入系统的能量：
1 2 Q + E1 + p1V1 = Q + m1 (u1 + cf 1 + gz1 ) + m1 p1v1 2 离开系统的能量： 离开系统的能量： 1 2 E2 + p2V2 + Wi = m2 (u 2 + cf 2 + gz 2 ) + m2 p2 v2 + Wi 2
第2章热力学第一定律
热力学能又称为内能（internal energy）,指体系 内部能量的总和，包括分子运动的平动能、转动能、 振动能、电子能、核能以及各种粒子之间的相互作 用势能等。以符号U表示，单位J。 ① 热力学能是状态函数，广度量； ② 热力学能的绝对值无法确定； ③ 单相、组成恒定、量定系统：U = f（T、V）
１、热力学的研究内容
经典热力学基本定律：
① 热力学第零定律： 热平衡定律（开尔文定律） ② 热力学第一定律： 能量转化与守恒定律 ③ 热力学第二定律： 判断过程的方向与限度 ④ 热力学第三定律： 计算规定熵
2、热力学研究方法及局限性
热力学研究方法：
以含有大量质点的宏观体系为研究对象，以两 个经典热力学定律为基础，用一系列热力学函数及
本堂课学习内容
§2.2
热力学第一定律
§2.3
恒容热、恒压热及焓
§2.2 热力学第一定律
1、热力学能（U) 2、热力学第一定律 3、焦耳实验
1、热力学能（thermodynamic energy）
•系统的总能量由以下三部分组成： ① 整体运动的动能；
② 在外力场中的势能；
③ 系统内部一切能量。 热力学研究对象为宏观静止体系，无整体运动； 并且一般没有特殊的外力场存在（电磁场、离心力场 等），因此只考虑系统内部能量。
4、热与功
•体积功（膨胀功）的计算:
W pamb dV
W PambdV
V1
V2
（ 向真空膨胀： W 0 pamb 0)
恒容过程： W 0 dV 0) （ 恒外压过程： W Pamb (V2 V1 ）
4、热与功
[例题] 300K下：
pamb p2 50kPa
１、热力学的研究内容
经典热力学基本定律：
① 热力学第零定律： 热平衡定律（开尔文定律） ② 热力学第一定律： 能量转化与守恒定律 ③ 热力学第二定律： 判断过程的方向与限度 ④ 热力学第三定律： 计算规定熵
2、热力学研究方法及局限性
热力学研究方法：
以含有大量质点的宏观体系为研究对象，以两 个经典热力学定律为基础，用一系列热力学函数及
本堂课学习内容
§2.2
热力学第一定律
§2.3
恒容热、恒压热及焓
§2.2 热力学第一定律
1、热力学能（U) 2、热力学第一定律 3、焦耳实验
1、热力学能（thermodynamic energy）
•系统的总能量由以下三部分组成： ① 整体运动的动能；
② 在外力场中的势能；
③ 系统内部一切能量。 热力学研究对象为宏观静止体系，无整体运动； 并且一般没有特殊的外力场存在（电磁场、离心力场 等），因此只考虑系统内部能量。
4、热与功
•体积功（膨胀功）的计算:
W pamb dV
W PambdV
V1
V2
（ 向真空膨胀： W 0 pamb 0)
恒容过程： W 0 dV 0) （ 恒外压过程： W Pamb (V2 V1 ）
4、热与功
[例题] 300K下：
pamb p2 50kPa
第二章热力学第一定律
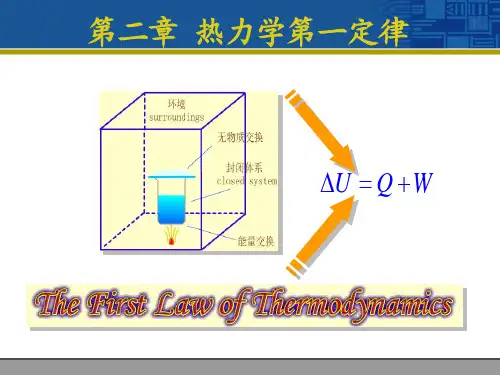
第二章 热力学第一定律（一）主要公式及其适用条件1、热力学第一定律的数学表示式∆U = Q + W 或 d U = đQ + đW规定系统吸热为正，放热为负；系统得功为正，对环境（或外界）作功为负。
式中U 称为热力学能（以前称为内能）。
上式适用于封闭系统一切过程能量的衡算。
2、体积功 （1）定义式đW = -p (环)V d 或W = ∑đW = -()V p d 21⎰环上式适用于一切过程体积功的计算。
（2）W r = -⎰21d V p式中：p 为系统的压力，W r 为可逆过程的体积功。
此式适用于封闭系统一切可逆过程体积功的计算。
（3）W = - p (V 2 - V 1) = nR(T 2 - T )此式适用于物质的量n 恒定的理想气体恒压变温过程。
（4）W = - p (环)(V 2 - V 1)此式适用于封闭系统恒外压过程。
（5）W = - nRT ln((V 2/ V 1) = - nRT ln((p 2/ p 1) 此式适用于一定量的理想气体恒温可逆过程。
（6）W = - p (V 2 - V 1) = -∆n g RT 式中∆n g 为过程前后气体物质量的增量。
此式适用于液态或固态物质所占体积与气态物质所占体积相比较可以忽略不计，气体为理想气体，恒压、恒温化学反应过程或相变过程。
（7）W = ∆U = nC V , m (T 2 - T )此式适用于n 、C V , m 恒定，理想气体绝热过程，不论过程是否可逆皆适用。
3、热力学能变（1）∆U =⎰21d m V,T T T nC = nC V , m (T 2 - T )此式适用于n 、C V , m 恒定的理想气体，单纯p 、V 、T 变化的一切过程；或者n 、C V , m 、V 恒定的任意单相纯物质的变温过程。
（2）∆U = Q V此式适用于非体积功W ' = 0、d V = 0的封闭系统所进行的一切过程。
4、焓的定义H = U + pV 5、焓变（1）∆H = ∆U + ∆(pV )式中∆(pV ) = p 2V 2 - p 1V 1，即系统p 与V 乘积的增量，只有恒压过程的∆(pV )在数值上才等于过程的体积功。
工程热力学 第二章 热力学第一定律
pv p2v2 p1v1
是系统为维持工质流动所需的功
对推动功的说明
1、与宏观流动有关，流动停止，推动功不存在 2、作用过程中，工质仅发生位置变化，无状态变化
3、w推＝pv与所处状态有关，是状态量 4、并非工质本身的能量（动能、位能）变化引起， 而由外界做出，流动工质所携带的能量
可理解为：由于工质的进出，外界与系统之间
The work depends on the process path
作功的说明
“作功”是系统与外界间的一种相互作用，是越过系统边
界的能量交换。
功是指作功过程中在传递着的能量的总称，过程一旦结束
就再无所谓功。
机械能与机械功、电能与电功等同吗？
系统可以拥有电能，机械能，但决不会拥有电功、机械功之类的功。 功只不过是特定条件下在过程中传递着的能量。
实质：能量守恒及转换定律在热现象中的应用
• 18世纪初，工业革命，热效率只有1% • 1842年，J.R. Mayer阐述热力学第一定律， 但没有引起重视
• 1840-1849年，Joule用多种实验的一致性 证明热力学第一定律，于1850年发表并得 到公认
热力学第一定律的普遍表达式
第一定律的表述： 热是能的一种，机械能变热能，或热能 变机械能的时候，他们之间的比值是一定的。 或：热可以变为功，功也可以变为热；一定量的热消失时 必定产生相应量的功；消耗一定量的功时，必出现与之相 应量的热。
系统是否作功应以过程在外界所引起的效果来判断，而不
应从系统的内部去寻找依据，对系统的内部来说无所谓 “功”。
功是有序能量传递。
传热
系统与外界之间的另一种相互作 用，是系统与外界之间依靠温差进行 的一种能量传递现象，所传递的能量 称放热为负
是系统为维持工质流动所需的功
对推动功的说明
1、与宏观流动有关，流动停止，推动功不存在 2、作用过程中，工质仅发生位置变化，无状态变化
3、w推＝pv与所处状态有关，是状态量 4、并非工质本身的能量（动能、位能）变化引起， 而由外界做出，流动工质所携带的能量
可理解为：由于工质的进出，外界与系统之间
The work depends on the process path
作功的说明
“作功”是系统与外界间的一种相互作用，是越过系统边
界的能量交换。
功是指作功过程中在传递着的能量的总称，过程一旦结束
就再无所谓功。
机械能与机械功、电能与电功等同吗？
系统可以拥有电能，机械能，但决不会拥有电功、机械功之类的功。 功只不过是特定条件下在过程中传递着的能量。
实质：能量守恒及转换定律在热现象中的应用
• 18世纪初，工业革命，热效率只有1% • 1842年，J.R. Mayer阐述热力学第一定律， 但没有引起重视
• 1840-1849年，Joule用多种实验的一致性 证明热力学第一定律，于1850年发表并得 到公认
热力学第一定律的普遍表达式
第一定律的表述： 热是能的一种，机械能变热能，或热能 变机械能的时候，他们之间的比值是一定的。 或：热可以变为功，功也可以变为热；一定量的热消失时 必定产生相应量的功；消耗一定量的功时，必出现与之相 应量的热。
系统是否作功应以过程在外界所引起的效果来判断，而不
应从系统的内部去寻找依据，对系统的内部来说无所谓 “功”。
功是有序能量传递。
传热
系统与外界之间的另一种相互作 用，是系统与外界之间依靠温差进行 的一种能量传递现象，所传递的能量 称放热为负
工程热力学-热力学第一定律
q w
对于可逆过程
du 0
上面得到的闭口系能量方程适用于任何工质、任何过程。
q du pdv
q u pdv
例题１
过 程 1—2 2—3 3—4 4—1
Q U W U Q W
热量 Q/ kJ 210 -210 功 W/ kJ 180 200 -300 内能变化量
上面的能量方程可写成
q h wt
多股物流进出系统时的稳定流动能量方程为
3. 稳定流动能量方程 稳定流动条件 τ时间内，系统内总能量的变化量
稳定流动条件
2
1
dE E2 E1 0
τ时间内，进入或离开控制体的质量
m m m
1
m2 常量
τ时间内，传入控制体的热量
2
1
Q Q 常量
τ时间内，控制体向外界输出的功
2
1
Wnet Wnet 常量
3. 稳定流动能量方程
稳定流动能量方程
2 c2 c12 Q (h2 gz2 )m (h1 gz1 )m Wnet 2 2
或整理成
2 c2 c12 Q (h2 h1 )m ( )m ( z2 z1 ) gm Wnet 2
1kg质量工质
2 c2 c12 q h g z wnet 2
2 c2 c12 Q (h2 h1 )m ( )m ( z2 z1 ) gm Wsh 2 2 c2 c12 q (h2 h1 ) ( ) ( z2 z1 ) g wsh 2
技术功
2 c2 c12 Wt ( )m ( z2 z1 ) gm Wsh 2 2 c2 c12 wt ( ) ( z2 z1 ) g wsh 2
第二章 热力学第一定律
式称为功，用W 表示。 (1) 分类：体积功We 、非体积功Wf
体积功We :在一定环境压力下系统的体积发生 变化时而与环境交换能量的形式。 非体积功Wf :除体积功之外的其它的功称为非体积功。
如电功、重力功、机械功、表面功。
(2) 说明：
a. 功是过程函数，其值与具体的实现途径有关； 微量功用W 表示
100 nRT ln 1 Wn 1 8.314 273.15 ln J 1574 J p2 50
p
︱-1574J ︱>︱-1325J ︱>︱ -1135J︱
W无限次膨胀 W两次膨胀 W一次膨胀
p
p1
一 次 膨胀 功
p
p1
二 次膨胀 功
p
p1
无 数 次 膨 胀功
二、热力学方法的特点和局限性
研究对象是由大量粒子组成的宏观系统。
①不涉及物质系统内部粒子的微观结构和个别
质点的行为 只管宏观，不管微观 只管两头，不管中间
②只涉及系统变化前后状态的宏观性质和外界
条件，不管中间的具体变化
③只考虑变化能否发生程度如何，不考虑时间因素
只管可能性，不管现实性
结论绝对可靠
第二章
nRT nRT pe pe p p nRT 1 p 1 1 2 1 8.314 273.15 (1 50 / 100) J
V
1135 J
③ 先于75kPa下膨胀至平衡‚再于50kPa下膨胀至终态
一种形式，从一个物体传递到另一个物体，即能量守恒 与转化定律。 b. 第一类永动机不能实现。
不需要外加能量就能源源不断对外做功的机器。 c. 隔离系统中，能量的形式可以转化，但能量
体积功We :在一定环境压力下系统的体积发生 变化时而与环境交换能量的形式。 非体积功Wf :除体积功之外的其它的功称为非体积功。
如电功、重力功、机械功、表面功。
(2) 说明：
a. 功是过程函数，其值与具体的实现途径有关； 微量功用W 表示
100 nRT ln 1 Wn 1 8.314 273.15 ln J 1574 J p2 50
p
︱-1574J ︱>︱-1325J ︱>︱ -1135J︱
W无限次膨胀 W两次膨胀 W一次膨胀
p
p1
一 次 膨胀 功
p
p1
二 次膨胀 功
p
p1
无 数 次 膨 胀功
二、热力学方法的特点和局限性
研究对象是由大量粒子组成的宏观系统。
①不涉及物质系统内部粒子的微观结构和个别
质点的行为 只管宏观，不管微观 只管两头，不管中间
②只涉及系统变化前后状态的宏观性质和外界
条件，不管中间的具体变化
③只考虑变化能否发生程度如何，不考虑时间因素
只管可能性，不管现实性
结论绝对可靠
第二章
nRT nRT pe pe p p nRT 1 p 1 1 2 1 8.314 273.15 (1 50 / 100) J
V
1135 J
③ 先于75kPa下膨胀至平衡‚再于50kPa下膨胀至终态
一种形式，从一个物体传递到另一个物体，即能量守恒 与转化定律。 b. 第一类永动机不能实现。
不需要外加能量就能源源不断对外做功的机器。 c. 隔离系统中，能量的形式可以转化，但能量
第二章 热力学第一定律
第二章
热力学第一定律
化学热力学
定义：化学热力学是将“热力学”运用于化学 领域而产生的一门研究化学反应过程中能量变 化的科学。 热力学—简单地说“是研究能量相互转换规律 的科学”。
化学热力学研究的主要内容： ①化学反应能否发生，若发生，其
能量是如何变化的； 恒容热QV
封闭系统, 当非体积功等于零(w’=0)
dU Q W QV U QV
物理意义
dV 0
封闭系统, 当不作非体积功时, 等容过程吸收的热
等于系统热力学能的增量, 所以QV只与系统初末态有关.
2 恒压热Qp和焓(enthalpy)
封闭系统, w’=0
恒压过程
是热。
热和功
功（work）
系统与环境之间传递的除热以外的其他能量
都称为功，用符号W表示。
W的取号： 环境对系统作功，W>0 系统对环境作功，W<0 Q和W的单位都用能量单位 “J” 表示 Q和W都不是状态函数，其数值与变化途径有关。
体积功: 系统体积变化而与环境交换的功，也叫膨胀功. 非体积功: 如表面功, 电功 等.
摩尔热容与温度的关系 热容与温度的函数关系因物质、物态和温度区 间的不同而有不同的形式。
C p,m (T ) a bT cT 2
Cp,m (T ) a' b'T 1 c'T 2
式中 a, b, c, a' , b' , c' 是经验常数，由各种物质本 身的特性决定，可从热力学数据表中查找。
当温度从T1 T2
QV CV dT nCV ,m dT
T2 T2 T1 T1
Q p C p dT nC p ,m dT
热力学第一定律
化学热力学
定义：化学热力学是将“热力学”运用于化学 领域而产生的一门研究化学反应过程中能量变 化的科学。 热力学—简单地说“是研究能量相互转换规律 的科学”。
化学热力学研究的主要内容： ①化学反应能否发生，若发生，其
能量是如何变化的； 恒容热QV
封闭系统, 当非体积功等于零(w’=0)
dU Q W QV U QV
物理意义
dV 0
封闭系统, 当不作非体积功时, 等容过程吸收的热
等于系统热力学能的增量, 所以QV只与系统初末态有关.
2 恒压热Qp和焓(enthalpy)
封闭系统, w’=0
恒压过程
是热。
热和功
功（work）
系统与环境之间传递的除热以外的其他能量
都称为功，用符号W表示。
W的取号： 环境对系统作功，W>0 系统对环境作功，W<0 Q和W的单位都用能量单位 “J” 表示 Q和W都不是状态函数，其数值与变化途径有关。
体积功: 系统体积变化而与环境交换的功，也叫膨胀功. 非体积功: 如表面功, 电功 等.
摩尔热容与温度的关系 热容与温度的函数关系因物质、物态和温度区 间的不同而有不同的形式。
C p,m (T ) a bT cT 2
Cp,m (T ) a' b'T 1 c'T 2
式中 a, b, c, a' , b' , c' 是经验常数，由各种物质本 身的特性决定，可从热力学数据表中查找。
当温度从T1 T2
QV CV dT nCV ,m dT
T2 T2 T1 T1
Q p C p dT nC p ,m dT
第二章 热力学第一定律
任何能量方程都是针对具体的系统的， 任何能量方程都是针对具体的系统的，所以同一问 题取不同系统可建立不同形式的能量方程， 题取不同系统可建立不同形式的能量方程，因此当你发 现自己建立的方程不同于你的学友建立的方程时， 现自己建立的方程不同于你的学友建立的方程时，不要 轻易否定任何方程， 轻易否定任何方程，而是按照能量守恒原理进行分析再 确定。 具体建立能量方程时还需注意下列两点： 确定。 具体建立能量方程时还需注意下列两点：在开 口系能量方程中引进（或排出）工质时引进（或排出） 口系能量方程中引进（或排出）工质时引进（或排出） 系统的能量应采用焓的概念而不是热力学能； 系统的能量应采用焓的概念而不是热力学能；只有在能 量越过边界时，才有功和热量在能量方程中出现。最后， 量越过边界时，才有功和热量在能量方程中出现。最后， 如何选择系统， 如何选择系统，对能量方程的建立和求解有时会有非常 大的影响，只有通过自己的实践和总结， 大的影响，只有通过自己的实践和总结，才能尽快掌握 选择一个合适的系统的关键。 选择一个合适的系统的关键。
第二章 热力学第一定律 13
二. 稳定流动的能量方程
一般情况下，能量转换装置都是在稳定条件下工作的。 一般情况下，能量转换装置都是在稳定条件下工作的。 稳定状态：各点的状态不随时间变化； 稳定状态：各点的状态不随时间变化； 稳定流动：系统内各处及进出口截面，工质的流量和流速不变。 稳定流动：系统内各处及进出口截面，工质的流量和流速不变。 系统与外界交换的热量和功量稳定不变。 系统与外界交换的热量和功量稳定不变。
2
2
wt = ∫1 pdv − ( p2v2 − p1v1 ) = − ∫1 vdp
2 2
由上式可知，准静态过程的技术 由上式可知， 功的大小可用过程线左边的面积来表 示。 忽略宏观动能和位能， 忽略宏观动能和位能，则有
第二章 热力学第一定律
量的总和，是状态参数。热量是传递过程中 的热能，不是状态参数。
思考
定量气体在等温过程中热力学能不变？
错误。气体的热力学能是温度和比体积的函
数，等温过程中虽然温度不变，但比体积可
能会发生改变，故热力学能也会改变。
思考
理想气体的热力学能只与温度有关。
正确。对于理想气体，因为分子间不存在相
互作用力，因此没有内位能。其热力学能仅 包括分子内动能。因此，理想气体热力学能 只是温度的单值函数。
二、外部储存能
需要用在系统外的参考坐标系测量的
参数来表示的能量，称为外部储存能，
它包括系统的宏观动能和重力位能。
质量为m的物体相对于系统外的参考坐 标以速度c运动时，其具有的宏观动能为：
1 2 Ek mc 2
重力场中质量为m的物体相对于系统外的 参考坐标系的高度为z时，其具有的重力位 能为：
滚球永动机
软臂永动机
19世纪有人设计了一种特殊机 构，它的臂可以弯曲。臂上有 槽，小球沿凹槽滚向伸长的臂 端，使力矩增大。转到另一侧， 软臂开始弯曲，向轴心靠拢。 设计者认为这样可以使机器获 得转矩。然而，他没有想到力 臂虽然缩短了，阻力却增大了， 转轮只能停止在原地。
软臂永动机
阿基米得螺旋永动机
分子热运动形成的内动能。它是温度的函数。
分子间相互作用形成的内位能。它是比体积的函 数。
维持一定分子结构的化学能、原子核内部的原子 能及电磁场作用下的电磁能等。
1、内动能
根据分子运动学说，组成气体的分子是处于不 断运动的状态中，不仅分子本身作直线运动、 旋转运动和相对于其它分子的振动，构成分子 的内部原子也在不断地振动，这些运动着的分 子与原子都具有动能，称为气体的内动能。 气体的内动能与气体的温度有关。气体的温 度越高，内动能越大。
思考
定量气体在等温过程中热力学能不变？
错误。气体的热力学能是温度和比体积的函
数，等温过程中虽然温度不变，但比体积可
能会发生改变，故热力学能也会改变。
思考
理想气体的热力学能只与温度有关。
正确。对于理想气体，因为分子间不存在相
互作用力，因此没有内位能。其热力学能仅 包括分子内动能。因此，理想气体热力学能 只是温度的单值函数。
二、外部储存能
需要用在系统外的参考坐标系测量的
参数来表示的能量，称为外部储存能，
它包括系统的宏观动能和重力位能。
质量为m的物体相对于系统外的参考坐 标以速度c运动时，其具有的宏观动能为：
1 2 Ek mc 2
重力场中质量为m的物体相对于系统外的 参考坐标系的高度为z时，其具有的重力位 能为：
滚球永动机
软臂永动机
19世纪有人设计了一种特殊机 构，它的臂可以弯曲。臂上有 槽，小球沿凹槽滚向伸长的臂 端，使力矩增大。转到另一侧， 软臂开始弯曲，向轴心靠拢。 设计者认为这样可以使机器获 得转矩。然而，他没有想到力 臂虽然缩短了，阻力却增大了， 转轮只能停止在原地。
软臂永动机
阿基米得螺旋永动机
分子热运动形成的内动能。它是温度的函数。
分子间相互作用形成的内位能。它是比体积的函 数。
维持一定分子结构的化学能、原子核内部的原子 能及电磁场作用下的电磁能等。
1、内动能
根据分子运动学说，组成气体的分子是处于不 断运动的状态中，不仅分子本身作直线运动、 旋转运动和相对于其它分子的振动，构成分子 的内部原子也在不断地振动，这些运动着的分 子与原子都具有动能，称为气体的内动能。 气体的内动能与气体的温度有关。气体的温 度越高，内动能越大。
第二章 热力学第一定律
2 1
v d p （适用于可逆过程）
对于微元可逆过程，
q dh vdp
技术功的图形表示
wt
2
vdp
1
20
2-5 稳定流动能量方程式的应用
工程上，除了喷管、扩压管外，常见热工设备 的进出口动、位能的变化一般都可以忽略不计。
q h ws
wt
ws
1. 热交换器
ws
0
q h 2 h1
2. 动力机械
q
0
w s h1 h 2
21
3. 绝热节流
( q = 0 , ws = 0 )
h1 h 2 0
注意：绝热节流过程不是定焓过程。
22
门窗紧闭房间用电冰箱降温
以房间为系统 闭口系能量方程
Q U W Q 0
绝热闭口系
Q H
1 2
m cf m g z W s
2
13
对于单位质量工质， 1 2 q h cf g z ws 2 以上两式称为开口系统的稳定流动能量方程。 对于微元过程 ，稳定流动能量方程写成
Q dH
1 2 1
m d cf m g d z W s
在热能与其它形式能的互相转换过程中， 能的总量始终不变。 不花费能量就可以产生功的第一类永动机 是不可能制造成功的。 进入系统的能量－离开系统的能量 = 系统储存能量的变化
5
2-3 闭口系统的热力学第一定律表达式 Q
ΔU
W
Q W U U 2 U1
Q U W
对于微元过程，
17
可以假定质量为m的工质从进口截面处的 状态1变化到出口截面处的状态2，从外界吸收 了热量Q,作了膨胀功W 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章热力学第一定律思考题1设有一电炉丝浸于水中，接上电源，通过电流一段时间。
如果按下列几种情况作为系统，试问A U ，Q，W为正为负还是为零？(1) 以电炉丝为系统；(2 )以电炉丝和水为系统；(3)以电炉丝、水、电源及其它一切有影响的部分为系统。
2设有一装置如图所示，(1)将隔板抽去以后，以空气为系统时，AJ, Q, W为正为负还是为零？(2)如右方小室亦有空气，不过压力较左方小，将隔板抽去以后，以所有空气为系统时，A U, Q , W为正为负还是为零？作业题1 (1)如果一系统从环境接受了160J的功，内能增加了200J，试问系统将吸收或是放出多少热？(2)一系统在膨胀过程中，对环境做了10 540J的功，同时吸收了27 110J的热，试问系统的内能变化为若干？[答案：⑴吸收40J; (2) 16 570J] 2在一礼堂中有950人在开会，每个人平均每小时向周围散发出4. 2xl05J的热量，如果以礼堂中的空气和椅子等为系统，则在开会时的开始20分钟内系统内能增加了多少？如果以礼堂中的空气、人和其它所有的东西为系统，则其AU = ?[答案:1.3 M08J;0]3 一蓄电池其端电压为12V,在输出电流为10A下工作2小时，这时蓄电池的内能减少了 1 265 000J,试求算此过程中蓄电池将吸收还是放岀多少热？[答案：放热401000J] 4体积为4.10dm3的理想气体作定温膨胀，其压力从106Pa降低到105Pa计算此过程所能作出的最大功为若干？[答案：9441J] 5在25C下，将50gN2作定温可逆压缩，从105Pa压级到2X106Pa，试计算此过程的功。
如果被压缩了的气体反抗恒定外压105Pa作定温膨胀到原来的状态，问此膨胀过程的功又为若干？[答案：-.33 X04J; 4.20 X03J] 6计算1mol理想气体在下列四个过程中所作的体积功。
已知始态体积为25dm3终态体积为100dm3;始态及终态温度均为100 Co(1) 向真空膨胀；(2) 在外压恒定为气体终态的压力下膨胀；(3) 先在外压恒定为体积等于50dm3时气体的平衡压力下膨胀，当膨胀到50dm3(此时温度仍为100C)以后，再在外压等于100 dm3时气体的平衡压力下膨胀；(4) 定温可逆膨胀。
试比较这四个过程的功。
比较的结果说明了什么问题？[答案:0; 2326J; 310l J; 4299J] 习题10试证明对遵守范德华方程的1mol实际气体来说，其定温可逆膨胀所作的功可用下式求算。
a（范德华方程为 p+兮（Vm 』尸RT ）< V m 丿习题11假设CO 2遵守范德华方程，试求算 1mol CO 2在27C 时由10dm 3定温可逆压缩到1dm 3所作的 功。
（所需范德华常数自己查表）。
[答案：一5 514J]习题12 1mol 液体水在100C 和标准压力下蒸发，试计算此过程的体积功。
（1）已知在100 C 和标准压力下，水蒸气的比体积 （体积除以质量）为1 677cm 3 • g -1,水的比体积为3-11.043cm • g 。
（2）假设水的体积比之蒸气的体积可略去不计，蒸气作为理想气体。
比较两者所得的结果，说明（2）的省略是否合理。
33[答案：3.057 X 103J ； 3.101 X103J] 习题13已知在0C 和标准压力下，冰的密度为0.917g -cm -3,水的密度为1.000g ・cm -3。
试计算在0°C 及标准压力下，1mol 冰熔化成水所需之功。
（要注意本题所需之功比之上题的涉及有蒸气的相变化的功是很 小的） [答案:-0.165J] 习题14在373K 和标推压力下，水的蒸发热为 4.067 X 04J mol -1，1mol 液态水体积为18.08cm 3，蒸气则为30 200cm 3。
试计算在该条件下 1mol 水蒸发成气的 A U 和A H 。
[答案：3.761 X 04J ; 4.067 X 04J] 习题15 一理想气体在保持定压 105Pa 下，从10dm 3膨胀到16dm 3,同时吸热1255J ，计算此过程的 A U和A H 。
[答案：655J ; 1 255J] 习题16假设N 2为理想气体。
在0C 和5X 105Pa 下，用2dm 3N 2作定温膨胀到压力为105Pa 。
（1） 如果是可逆膨胀；（2）如果膨胀是在外压恒定为 105Pa 的条件下进行。
试计算此两过程的 Q 、W 、A U 和少。
[答案：(1)1 609J ; 0; (2)800 J ; 0]习题18 有3mol 双原子分子理想气体由 25 C 加热列150C ，试计算此过程的△ U 和厶H 。
[答案：7.79X 103J ； 1.09 X 104J]5习题19 有1mol 单原子分子理想气体在 0C ，10 Pa 时经一变化过程，体积增大一倍，△ H = 2 092J ， Q=1 674J 。
（1）试求算终态的温度、压力及此过程的△ U 和W ;⑵如果该气体经定温和定容两步可逆过程到 达上述终态，试计算 Q 、W 、A U 和厶H 。
习题20[答案:(1)373.7K ，6.84X 104 Pa, 1255J ，419J ， (2)2828 J ，1573J ，1255J,2092J] 已知 300K 时NH 3 的.曲 m i =840 J - m -3 • mol -1, CV,m=37.3J • K " • mol -1。
当 1mol NH 3 1刃T 气经一压缩过程其体积减少 10 cm 3而温度上升2度时，试计算此过程的△ U[答案：74.6J]习题21试证明对任何物质来说W = RTlnVm,2』 Vm,1』+aQ 丄Jm,2 V m,1 ；习题仃试由=°及多T=0证明理想气体的 =0及0。
习题25 一物质在一定范围内的平均定压摩尔热容可定义为C — _ Q pp ，m_ nT2h1其中n 为物质的量。
已知 NH 3的T T 2 ］C = 33.64+2.93X10 ； 42.13X10-5p，m I KK J试求算NH 3在0〜500C 之间的平均定压摩尔热容 C p m习题26已知N 2和。
2的定压摩尔热容与温度的关系式分别为C p m (N 2 )= (7.87 也.27>10fCp,m(O 2 )= 36.162P.845汉 10“T Y.310>105—— ' K (T / K 试求空气的C p ,m 与温度的关系式应为如何？习题271molH 2在25 C 、105 Pa 下，经绝热可逆过程压缩到体积为终态压力P 2；⑶过程的 W,A U 和厶H 。
（ H 2的C V ，m 可根据它是双原子的理想气体求算）[答案： 565K ； 9.39 X 105 Pa ； 5550J ； 5550J ；7769J] 习题28 25C 的空气从106 Pa 绝热可逆膨胀到105 Pa,如果做了 1.5 X 104J 的功，计算空气的物质的量。
（假设空气为理想气体，空气的热容数据可查表或作一近似计算）[答案：5.01mol]习题29某理想气体的C p,m =35.90J • K -1 • mol -1,⑴当2mol 此气体在25C, 1.5 X 106 Pa 时，作绝热 可逆膨胀到最后压力为5X 105 Pa ；⑵当此气体在外压恒定为 5X 105 Pa 时作绝热快速膨胀；试分别求算上述两过程终态的 T 和V 及过程的 W 、△ U 和厶H 。
k 別,T 」0丿p [[I 印.T 一© .V习题22计算1gN 2在常压下由600C 冷却到20C 时所放出的热，所需数据自己查找。
1Cp "CV2C p -CV习题23试求算2mol100 C, 4 X 104pa 的水蒸气变成I00C 及标准压力的水时，此过程的△ 水蒸气可视为理想气体，液体水的体积可忽略不计。
已知水的摩尔气化热为［答案：629J ］U 和厶H 。
设4 0670J • mol -1。
［答案：一75 138J ;— 81 340J ］习题24已知任何物质的Cp-C V2 — TV其中a 为膨胀系数，B 为压缩系数。
现已查得 25C 时液体水的定容热容X 10「4K T, B =4.44X 1oT °Pa 「S而水的18X 10「6m C v ，m=75.2J • K 1 • mol", 3 • mol -1。
试计算液体水在25 C 时的C p ,m =?［答案：75.7J • K t a =2.1-mo 「］JK -1 卽ol -1［答案：41.4J ・K t -mo 「］mol -1JjK -1 却ol -15dm 3,试求⑴终态温度T 2；⑵[答案：⑴231K ; 7.68dm3；-3697J; -3697J;-4811J;⑵252K; 8.38 dm3; 2538J; -2538J; -3303J] 习题30 1mol某双原子分子理想气体发生可逆膨胀：(1)从2 dm3, 106 Pa定温可逆膨胀到5x 105 Pa;⑵从2 dm3, 106 Pa绝热膨胀到5x 105 Pa。
⑴试求算过程⑴和⑵的W, Q ,△U和厶H;⑵大致画出过程⑴和⑵在p—V图上的形状；⑶在p—V图上画岀第三个过程将上述两过程的终态相连，试问这第三个过程有何特点(是定容还是定压)？[答案：⑴ 1386J; 1386J; 0; 0;⑵ 919J; 0; -919J; -1286J] 习题31某高压容器所含的气体可能是N2或是Ar。
今在25C时取出一些样品由5 dm3绝热可逆膨胀到6 dm3，发现温度下降了2「C，试判断容器中为何气体？[答案：N2] 在573K及0至6X10-6Pa的范围内，N2(气)的焦耳一汤姆逊系数可近似用下式表示-7 -14 -1叶T=[1.40 X10 253 X10 (p/Pa)]K • Pa假设此式与温度无关。
N2(气自6X10-6Pa作节流膨胀到2X10-6Pa，求温度变化。
[答案：A T= - 0.16K] 习题33 已知CO2的旳-T=1.07 X10-5K • Pa-1，C p,m=36.6J • K-1• mol-1，试求算50g CO2在25 C下由105Pa定温压缩到106Pa时的少。
如果实验气体是理想气体，则A H又应为何值？[答案：-401J ; 0]-5 -c习题34 假设He为理想气体。
1molHe由2X10 Pa、0C变为10 Pa、50 C，可经两个不同的途径：(1)先定压加热，在定温可逆膨胀；(2)先定温可逆膨胀；再定压加热。
试分别计算此二途径的Q、W、AJ、A H。