第二章5典型环节.

登录注册主页关于我们控制理论教学制冷机仿真热工设备仿真论坛博客联系我们您当前的位置：主页> 控制理论教学> 控制理论教程> 第二章> 2.3习题演练控制系统实验控制理论教程学生作业档案教师办公室典型作业展示常见问题第一章自动控制的基本概念第二章控制系统的数学描述第三章控制系统的时域分析第四章控制系统的频域分析第五章过程控制2.3 控制系统的典型环节2.3 控制系统的典型环节自动控制系统是由不同功能的元件构成的。

从物理结构上看，控制系统的类型很多，相互之间差别很大，似乎没有共同之处。

在对控制系统进行分析研究时，我们更强调系统的动态特性。

具有相同动态特性或者说具有相同传递函数的所有不同物理结构，不同工作原理的元器件，我们都认为是同一环节。

所以，环节是按动态特性对控制系统各部分进行分类的。

应用环节的概念，从物理结构上千差万别的控制系统中，我们就发现，他们都是有为数不多的某些环节组成的。

这些环节成为典型环节或基本环节。

经典控制理论中，常见的典型环节有以下六种。

2.3.1 比例环节比例环节是最常见、最简单的一种环节。

比例环节的输出变量y(t)与输入变量x(t)之间满足下列关系(2.24)比例环节的传递函数为(2.25)式中K为放大系数或增益。

杠杆、齿轮变速器、电子放大器等在一定条件下都可以看作比例环节。

例10 图2.10 是一个集成运算放大电路，输入电压为，输出电压为，为输入电阻，为反馈电阻。

我们现在求取这个电路的传递函数。

解从电子线路的知识我们知道这是一个比例环节，其输入电压与输出电压的关系是(2.26)按传递函数的定义，可以得到(2.27)式中，可见这是一个比例环节。

如果我们给比例环节输入一个阶跃信号，他的输出同样也是一个阶跃信号。

阶跃信号是这样一种函数(2.28)式中为常量。

当时，称阶跃信号为单位阶跃信号。

阶跃输入下比例环节的输出如图2.11 所示。

比例环节将原信号放大了K倍。

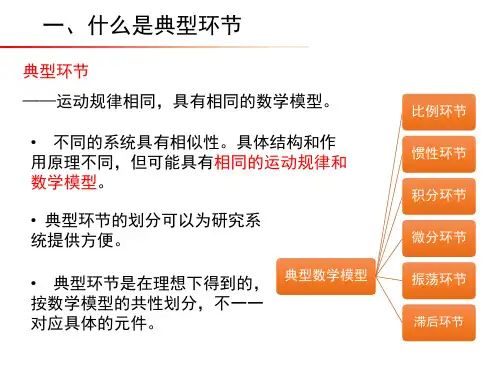
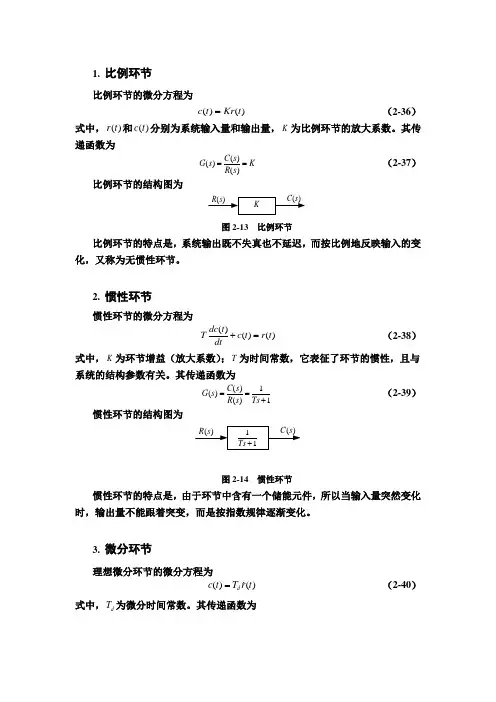
1. 比例环节 比例环节的微分方程为()()c t Kr t = （2-36）式中，()r t 和()c t 分别为系统输入量和输出量，K 为比例环节的放大系数。

其传递函数为()()()C s G s KR s ==（2-37） 比例环节的结构图为图2-13 比例环节比例环节的特点是，系统输出既不失真也不延迟，而按比例地反映输入的变化，又称为无惯性环节。

2. 惯性环节 惯性环节的微分方程为()()()dc t Tc t r t dt +=（2-38） 式中，K 为环节增益（放大系数）；T 为时间常数，它表征了环节的惯性，且与系统的结构参数有关。

其传递函数为()1()()1C s G s R s Ts ==+（2-39） 惯性环节的结构图为图2-14 惯性环节惯性环节的特点是，由于环节中含有一个储能元件，所以当输入量突然变化时，输出量不能跟着突变，而是按指数规律逐渐变化。

3. 微分环节理想微分环节的微分方程为()()d c t T r t =（2-40）式中，d T 为微分时间常数。

其传递函数为()()()d C s G s T sR s == （2-41） 微分环节的结构图为图2-15 微分环节微分环节的特点是，系统输出量正比于输入量的微分，即输出量反映输入量的变化率，而不反映输入量本身的大小。

因此，可由微分环节来反映输入量的变化趋势，使控制作用提前。

实际中常利用微分环节改善系统的动态性能。

但要注意，当输入为单位阶跃响应函数时，输出就是脉冲函数，这在实际中是不可能的。

因此，微分环节一般不单独存在，而是与其他环节（如比例环节）同时存在的。

4. 积分环节积分环节的微分方程为()()i T c t r t = （2-42）式中，i T 为微分时间常数。

其传递函数为()1()()i C s G s R s T s==（2-43）积分环节的结构图为图2-16 积分环节积分环节的特点是，系统输出量正比于输入量对时间的积分，输出量呈线性增长。

第一章3解：1）工作原理：电压u2反映大门的实际位置，电压u1由开（关）门开关的指令状态决定，两电压之差△ u= u1 —u2驱动伺服电动机，进而通过传动装置控制大门的开启。

当大门在打开位置，u2= u上：如合上开门开关，u1 = u 上, △ u = 0,大门不动作；如合上关门开关，u1= u下，△ u<0,大门逐渐关闭，直至完全关闭，使△ u= 0。

当大门在关闭位置，u2 二u 下：如合上开门开关，u1 = u上, △ u>0,大门执行开门指令，直至完全打开，使△ u = 0; 如合上关门开关，u1 = u下，△ u= 0,大门不动作。

2）控制系统方框图解：1）控制系统方框图a）系统方a ）水箱是控制对象，水箱的水位是被控量，水位的给定值 h '由浮球顶杆的长度给定，杠 杆平衡时，进水阀位于某一开度，水位保持在给定值。

当有扰动（水的使用流出量和给水 压力的波动）时，水位发生降低（升高），浮球位置也随着降低（升高），通过杠杆机构是 进水阀的开度增大（减小），进入水箱的水流量增加（减小），水位升高（降低），浮球也随 之升高（降低），进水阀开度增大（减小）量减小，直至达到新的水位平衡。

此为连续控制 系统。

b ）水箱是控制对象，水箱的水位是被控量，水位的给定值 h '由浮球拉杆的长度给定。

杠 杆平衡时，进水阀位于某一开度，水位保持在给定值。

当有扰动（水的使用流出量和给水 压力的波动）时，水位发生降低（升高），浮球位置也随着降低（升高），到一定程度后， 在浮球拉杆的带动下，电磁阀开关被闭合（断开），进水阀门完全打开（关闭），开始进水（断水），水位升高（降低），浮球也随之升高（降低），直至达到给定的水位高度。

随后水 位进一步发生升高（降低），到一定程度后，电磁阀又发生一次打开（闭合）。

此系统是离 散控制系统。

2-1 解：（c ）确定输入输出变量（u1，u2）得到：CR 2dU 1（1 匹）u 2 =CR 2dU 1-R2u 1 dt R 1 dt R一阶微分方程（e ）确定输入输出变量（u1，u2）消去i 得到：（& R 埒汁2牛亡 一阶微分方程第二章2- 2解：1）确定输入、输出变量f （t ） 、X 2□2）工作原理：b ）系统方框图干f(t)-fK1⑴-fB 1⑴-fBMF^d^- - 1 -(s 2) (s 1) (s 1)2M(s)=0, 4) D(s)=0,得到极点：一1, M(s)=0, 得到零点：2) 对各元件列微分方程:2f f f _ d X 2(t)fB3 ~'T K2-'T B 2= m 2K1B3 dt 2=K 1X 1； f B1 = B 1 -- -dt B d (x 1 - x2) =B 3 甬；fK2 = K 2X23)4) 5) 拉氏变换.F(s)—KX(s)—B 1SX1G)—B3$(X 1(s) —X 2(s)] = gs 2X 1(s) 叉'B 3S[X 1(s) -X 2(s)] -K 2X2G)-B 2SX2G ) = m 2S 2X 2(s) 消去中间变量： 拉氏反变换：mi|m 2 d 4X d 3X d 2X$ (B 1m 2 七2口1 B s mh B s mJ $(B 1B 3 B 1B 2 B s B ?心口2 ^心)/dt dt dt 2_3(K 1B 2 K 1B 3 K 2B 1 K 2B 3)等 K 1g 弋詈解:(2) (4)1 1 11 1 1 — 29 s 49 s 13 (s 1)(5)(6)-0.25 2s 0.5 2 22 2.5 s2- 5解：1)D(s)=0, M(s)=0,2) D(s)=0, M(s)=0,得到极点：0,0,-2,-5得到零点：一 1 , ' 得到极点：一 2, — 1, —2 得到零点：0 , 0 , — 1+ □0 +oci3) D(s)=O, 得到极点：0,得到零点：一2,2- 8解：1) a )建立微分方程b) 拉氏变换 c) 画单元框图(略) d) 画系统框图mx o (t) = f k (t) f Bl (t) - f B2(t) f k (t)二 k(X i (t) —x °(t))ms 2X o (s) = F k (s) F BI (S ) -F B 2(S )b) 拉氏变换：F k (s )=k (X i (s )-X o (s))F Bi (s)=B i S (X j (s)—X o (s))F B 2(S )工 B 2S X O (S )c) 绘制单元方框图(略)4)绘制系统框图Fi ( s )2)a)建立微分方程:f B1(t) B id (N (t)-")) dtf B2 (t)=B 2 dX o (t) dt由于扰动产生的输出为:要消除扰动对输出的影响，必须使 X o2(S )=0 得到：QK 2K 3G o (s) -K 3K 4S =0第三章3- 1解：1)法一：一阶惯性环节的调整时间为 4T ,输出达稳态值的98%故: 4T = 1min ,得到：T = 15s法二：求出一阶惯性环节的单位阶跃时间响应，代入，求出。