第二章 典型环节的数学模型(2-1)
- 格式：ppt
- 大小：1.10 MB
- 文档页数：26
下载文档原格式
合集下载
第2章系统的数学模型02精选全文完整版
的传递函数。
图2-13 油缸－负载系统
解：液压缸的作用力F
F pA
式中p—进油压力
A—液压缸工作面积
该力用于克服阻尼负载和弹性负载，即
dx
F Bc
kx
dt
式中x —液压缸输出位移
Bc—阻尼系数
K —弹簧刚度
合并以上两式，得液压缸的运动方程式：
dx
Bc
kx Ap
dt
传递函数为
A
4
dt
dt
dt
dt
解：按（2-53）式，则传递函数为
Y ( s)
6s 7
（１） G ( s )
3
X ( s) 5s 2s 2 s 2
（２） G ( s )
Y (பைடு நூலகம்s)
4
4
X ( s) s 2s 3 6s 2 3s 2
二、典型环节的传递函数
bm s m bm 1 s m 1 ...... b1 s b0
dt
dx
b1
b0 x
dt
（2-51）
式中，n≥m; an、bm均为系统结构参数所决定的定
常数 。（n，m=0、1、2、3…）
如果变量及其各阶导数初值为零，取等式两边拉
氏变换后得
an s nY ( s ) an1 s n1Y ( s ) a1 sY ( s ) a0Y ( s )
X(s)=0 系统的特征方程，→ 特征根。
特征方程决定着系统的动态特性。
X(s) 中s的最高阶次等于系统的阶次。
b0
当s=0时 G (0) K 系统的放大系数或增益
a0
！从微分方程的角度看，此时相当于所有的导
图2-13 油缸－负载系统
解：液压缸的作用力F
F pA
式中p—进油压力
A—液压缸工作面积
该力用于克服阻尼负载和弹性负载，即
dx
F Bc
kx
dt
式中x —液压缸输出位移
Bc—阻尼系数
K —弹簧刚度
合并以上两式，得液压缸的运动方程式：
dx
Bc
kx Ap
dt
传递函数为
A
4
dt
dt
dt
dt
解：按（2-53）式，则传递函数为
Y ( s)
6s 7
（１） G ( s )
3
X ( s) 5s 2s 2 s 2
（２） G ( s )
Y (பைடு நூலகம்s)
4
4
X ( s) s 2s 3 6s 2 3s 2
二、典型环节的传递函数
bm s m bm 1 s m 1 ...... b1 s b0
dt
dx
b1
b0 x
dt
（2-51）
式中，n≥m; an、bm均为系统结构参数所决定的定
常数 。（n，m=0、1、2、3…）
如果变量及其各阶导数初值为零，取等式两边拉
氏变换后得
an s nY ( s ) an1 s n1Y ( s ) a1 sY ( s ) a0Y ( s )
X(s)=0 系统的特征方程，→ 特征根。
特征方程决定着系统的动态特性。
X(s) 中s的最高阶次等于系统的阶次。
b0
当s=0时 G (0) K 系统的放大系数或增益
a0
！从微分方程的角度看，此时相当于所有的导
第4讲 典型环节
� 典型环节示例 � 比例环节
输出量不失真、无惯性、快速地跟随输入量，两者成 比例关系。
其运动方程为：xo(t)=Kxi(t)
xo(t)、xi(t)——分别为环节的输出量和输入量； K——比例系数，等于输出量与输入量之比。
比例环节的传递函数为： X o ( s) G( s) = =K X i ( s)
传递函数： G ( s ) = K τ 2 s 2 + 2ξ τs + 1
(
)
式中，τ——时间常数 ξ——阻尼比，对于二阶微分环节， 0<ξ<1 K——比例系数
系统数学模型 第二章 � 积分环节
输出量正比于输入量对时间的积分。 运动方程为： xo (t ) = 1 ∫ t xi (t )dt 0
T
车初始位置距平衡点1.0，则所建立模型如图示。
F c k 系统微分方程 ̇ ̇= − x ̇− x x m m m
若外力输入F=0，仿真所得示 波器窗口小车位移随时间变 化的轨迹如图。
F
为0
初值为1
第二章 系统数学模型
质量—弹簧—阻尼系统
F
F如下图 系统输入 系统输入F
系统输出 x如下图所示 系统输出x
微分环节的输出是输入的导数，即输出反映了 输入信号的变化趋势，从而给系统以有关输入 变化趋势的预告。因此， 微分环节常用来改善 变化趋势的预告。因此，微分环节常用来改善 控制系统的动态性能。
第二章 系统数学模型
� 二阶微分环节 运动方程：
⎡ 2 d2 ⎤ d xo (t ) = K ⎢τ x (t ) + 2ξ τ xi (t ) + xi (t )⎥, 0 < ξ < 1 2 i dt ⎣ dt ⎦
输出量不失真、无惯性、快速地跟随输入量，两者成 比例关系。
其运动方程为：xo(t)=Kxi(t)
xo(t)、xi(t)——分别为环节的输出量和输入量； K——比例系数，等于输出量与输入量之比。
比例环节的传递函数为： X o ( s) G( s) = =K X i ( s)
传递函数： G ( s ) = K τ 2 s 2 + 2ξ τs + 1
(
)
式中，τ——时间常数 ξ——阻尼比，对于二阶微分环节， 0<ξ<1 K——比例系数
系统数学模型 第二章 � 积分环节
输出量正比于输入量对时间的积分。 运动方程为： xo (t ) = 1 ∫ t xi (t )dt 0
T
车初始位置距平衡点1.0，则所建立模型如图示。
F c k 系统微分方程 ̇ ̇= − x ̇− x x m m m
若外力输入F=0，仿真所得示 波器窗口小车位移随时间变 化的轨迹如图。
F
为0
初值为1
第二章 系统数学模型
质量—弹簧—阻尼系统
F
F如下图 系统输入 系统输入F
系统输出 x如下图所示 系统输出x
微分环节的输出是输入的导数，即输出反映了 输入信号的变化趋势，从而给系统以有关输入 变化趋势的预告。因此， 微分环节常用来改善 变化趋势的预告。因此，微分环节常用来改善 控制系统的动态性能。
第二章 系统数学模型
� 二阶微分环节 运动方程：
⎡ 2 d2 ⎤ d xo (t ) = K ⎢τ x (t ) + 2ξ τ xi (t ) + xi (t )⎥, 0 < ξ < 1 2 i dt ⎣ dt ⎦
自动控制原理课件 第二章 线性系统的数学模型
c(t ) e
dt Leabharlann t
c( s )
g ( ) r ( ) d e s ( ) d 0 0 g ( )e s r ( )e s d d 0 0
0
g ( )e
5) 闭环系统传递函数G(s)的分母并令其为0，就是系统的特征方 程。
• 涉及的是线性系统 非线性系统必须 进行线性化处理
§2-6 信号流程图
系统很复杂，为方便研究，也为了与 实际对应，通常将复杂系统分解为 若干典型环节的连接
数学模型的定义 数学模型： 描述系统变量间相互关系的动态性能的运动方程 建立数学模型的方法：
解析法: 依据系统及元件各变量之间所遵循的物理或化学规律列写出相 应的数学关系式，建立模型。 自动控制系统的组成可以是电气的，机械的，液压的，气动的等等，然 而描述这些系统的数学模型却可以是相同的。因此，通过数学模型来研 究自动控制系统，就摆脱了各种类型系统的外部关系而抓住这些系统的 共同运动规律，控制系统的数学模型是通过物理学，化学，生物学等定 律来描述的，如机械系统的牛顿定律，电气系统的克希霍夫定律等都是 用来描述系统模型的基本定律。 实验法: 人为地对系统施加某种测试信号，记录其输出响应，并用适当 的数学模型进行逼近。这种方法也称为系统辨识。 数学模型的形式 时间域： 复数域： 频率域： 微分方程 差分方程 传递函数 结构图 频率特性 状态方程
1 例1 : F ( s) ( s 1)(s 2)(s 3) c c c 1 2 3 s 1 s 2 s 3
1 1 c1 [ ( s 1)]s 1 ( s 1)(s 2)(s 3) 6 1 1 c2 [ ( s 2)]s 2 ( s 1)(s 2)(s 3) 15 1 1 c3 [ ( s 3)]s 3 ( s 1)(s 2)(s 3) 10 1 1 1 1 1 1 F ( s) 6 s 1 15 s 2 10 s 3 1 1 1 f (t ) e t e 2t e 3t 6 15 10
自动控制原理：第二章--控制系统数学模型全
TaTLma KJe K
dMdML m dtdt
L
Tm
Ra J K eKm
——机电时间常数(秒)；
Ta
La Ra
—电动机电枢回路时间常数 (秒)
若输出为电动机的转角q ，则有
TaTm
d 3q
dt 3
Tm
d 2q
dt 2
dq
dt
1 Ke
ua
Tm J
ML
TaTm J
dM L dt
—— 三阶线性定常微分方程 9
（1）根据克希霍夫定律可写出原始方程式
（（23））式消LuLCcdd中去(titd)i中2d是utRc间2(中Cti1)变间C1量iR变dCti量idd后udt，ct，(t它)u输r与u(入tc输)(输t)出出uu微rc((tt)分)有方如程下式关系
或
T1T2
d 2uc (t) dt 2
T2
duc (t) dt
扰动输入为负载转矩ML。 （1）列各元件方程式。电动机方程式为：
TaTm
d 2w
dt 2
测输T速Km出发td为d电wt电测压机速w 反 K馈1e系ua数
Tm J
M反L馈 电TaJT压m
dM L dt
ua Kae ut Ktw e ur ut 12
（2）消去中间变量。从以上各式中消去中间变
量ua，e，ut，最后得到系统的微分方程式
线性(或线性化)定常系统在零初始条件下， 输出量的拉氏变换与输入量的拉氏变换之比 称为传递函数。
令线C性(s定)=常L[c系(t统)]，由R下(s)述=Ln阶[r(微t)]分，方在程初描始述条：件为零
时[[aab，nnmbssdmdn进mt+ndn+dt行acmmbn(tm拉-r1)-(s1t氏ns)-am1变n+-1b1+…m换dd…1t+，nndd+1a1t得mm1bcs1(11到+ts)r+a关(t0b)]于0C]的RD(sM的s的a(()分s1s(分))=代sdbd为母)t1子为数cd传d多(tt多传方)r递项(项t程递函)式a式0函数c。b(0数tr) (t)
自动控制理论_哈尔滨工业大学_2 第2章线性系统的数学模型_(2.4.1) 典型环节的传递函数PPT
0
t
积分环节在单位阶跃输入下的响应
例：积分器
i2
C
ui R
_
i1
uo
+i1 i2Fra bibliotek1 Rui
(t)
C
d dt
u0
(t )
uo
(t)
1 RC
ui (t)dt
G(s) Uo (s) 1 1 Ui (s) RC s
二、几种典型环节的数学模型
4.微分环节
c(t) d r(t)
斜率1/T
0τ
t
例： • 汽车加速、火箭升空； ——作用力和输出速度
• 加热系统； ——加热量和温度变化
• 励磁回路； ——输入电压和励磁电流
惯性大小用τ来量度。 ——τ越大，接近目标值越慢 ，惯性越大；τ越小，接近 目标值越快，惯性越小。
几乎任何物理系统都包含 大大小小的惯性。
二、几种典型环节的数学模型
滞后环节
二、几种典型环节的数学模型
1.比例环节
y(t) Ku(t)
G(s) Y(s) K U (s)
K——称为比例系数或放大系数，也称为环节的增益，有量纲。
输出量无失真、无滞后、成比例地复现输入。
• 无弹性变形的杠杆；
——作用力和输出力
• 忽略非线性和时间迟后的运算放大器；
——比例放大器的输入电压和输出电压
τ＝RC—时间常数
当 r(t) 1(t) 时， R(s) 1
s
Y(s) s 1 1 s 1 s s 1
t
y(t) e
t=0时，输出幅值为1；
t→∞时，指数衰减至0。
二、几种典型环节的数学模型
控制工程基础3-第2章 (数学模型1：微分方程,传递函数)
at
sa
2
• 拉氏变换的基本性质 (1) 线性性质
L[af1 (t ) bf 2 (t )] aL[ f1 (t )] bL[ f 2 (t )]
原函数之和的拉氏变换等于各原函数的拉氏变换之和。 (2) 微分性质 L 若[ f (t )] F ( s ) ，则有 L[ f (t )] sF ( s) f (0) f(0)为原函数f(t) 在t=0时的初始值。 (3) 积分性质 则 若 L[ f (t )] F ( s )
该标准型为二阶线性常系数微分方程，系统中存在两个储能元件质 量和弹簧，故方程式左端最高阶次为二。
-
机械旋转系统
• [例2]：设有一个惯性负载和粘性摩擦阻尼器组成的机械 旋转系统，试列出以外力矩M(t)为输入信号，角位移 θ(t)为输出信号的数学模型。
M
J
θ
f
解：
1）确定输入量、输出量
M J θ f
F(t) m f
K x(t)
图 2 2 机 械 系 统
d 2x 3）由牛顿第二定律写原始方程： F F (t ) Fk (t ) F f (t ) m 2 dt dx Fk (t ) kx F f (t ) f 4）写中间变量与输出变量的关系式： dt 2 d x dx 5）将上式代入原始方程消中间变量得： m 2 kx f F (t ) dt dt m d 2 x f dx 1 x F (t ) 6）整理成标准型： 令 T2 m T f 2 k dt k dt k m f 2 k k dx 1 2 d x 则方程化为： Tm dt 2 T f dt x k F (t )
第二章 控制系统的数学模型
导 为什么要介绍本章? 分析、设计控制系统的第一步是建立系统的数学模 型。 读
第二章_典型环节
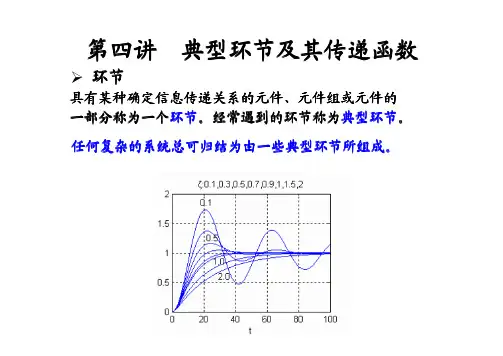
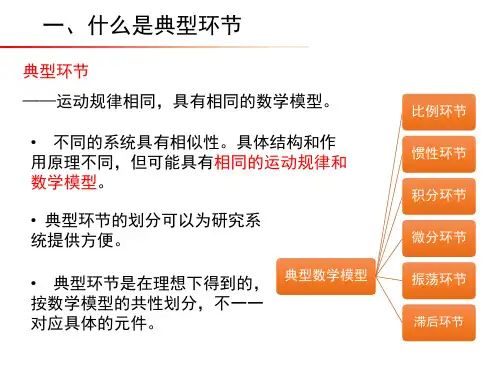
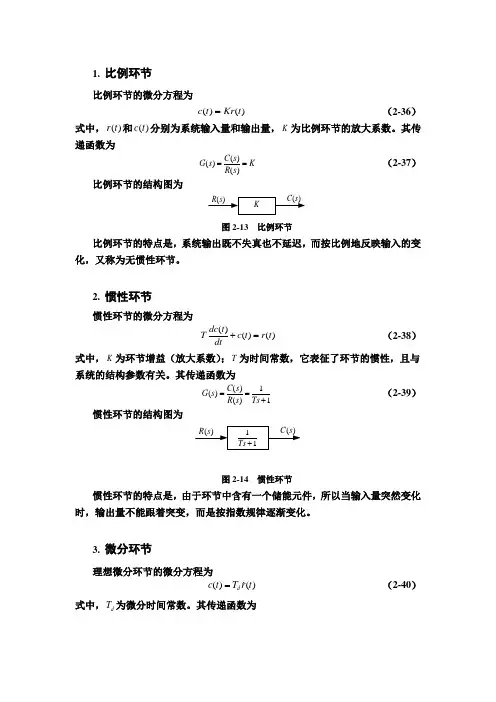
1. 比例环节 比例环节的微分方程为()()c t Kr t = （2-36）式中，()r t 和()c t 分别为系统输入量和输出量，K 为比例环节的放大系数。
其传递函数为()()()C s G s KR s ==（2-37） 比例环节的结构图为图2-13 比例环节比例环节的特点是，系统输出既不失真也不延迟，而按比例地反映输入的变化，又称为无惯性环节。
2. 惯性环节 惯性环节的微分方程为()()()dc t Tc t r t dt +=（2-38） 式中，K 为环节增益（放大系数）；T 为时间常数，它表征了环节的惯性，且与系统的结构参数有关。
其传递函数为()1()()1C s G s R s Ts ==+（2-39） 惯性环节的结构图为图2-14 惯性环节惯性环节的特点是，由于环节中含有一个储能元件，所以当输入量突然变化时，输出量不能跟着突变，而是按指数规律逐渐变化。
3. 微分环节理想微分环节的微分方程为()()d c t T r t =（2-40）式中，d T 为微分时间常数。
其传递函数为()()()d C s G s T sR s == （2-41） 微分环节的结构图为图2-15 微分环节微分环节的特点是，系统输出量正比于输入量的微分，即输出量反映输入量的变化率，而不反映输入量本身的大小。
因此，可由微分环节来反映输入量的变化趋势，使控制作用提前。
实际中常利用微分环节改善系统的动态性能。
但要注意，当输入为单位阶跃响应函数时，输出就是脉冲函数，这在实际中是不可能的。
因此，微分环节一般不单独存在，而是与其他环节（如比例环节）同时存在的。
4. 积分环节积分环节的微分方程为()()i T c t r t = （2-42）式中，i T 为微分时间常数。
其传递函数为()1()()i C s G s R s T s==（2-43）积分环节的结构图为图2-16 积分环节积分环节的特点是，系统输出量正比于输入量对时间的积分，输出量呈线性增长。
典型环节的数学模型
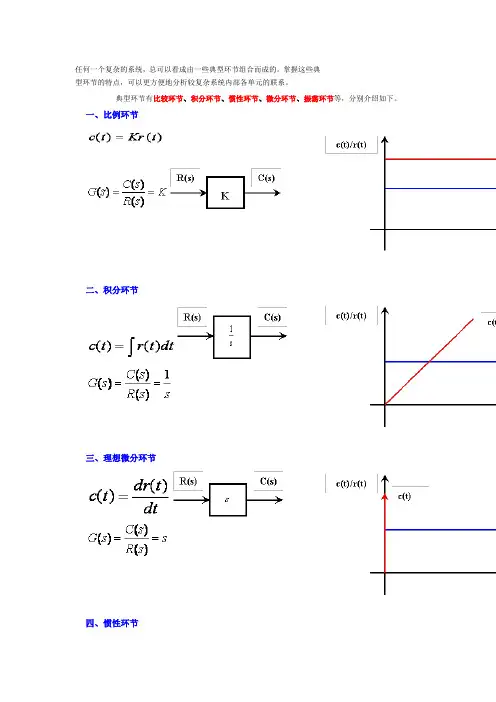
任何一个复杂的系统，总可以看成由一些典型环节组合而成的。
掌握这些典
型环节的特点，可以更方便地分析较复杂系统内部各单元的联系。
典型环节有比较环节、积分环节、惯性环节、微分环节、振荡环节等，分别介绍如下。
一、比例环节
二、积分环节
三、理想微分环节
四、惯性环节
五、振荡环节
特别注意：当0〈§〈1时称为振荡环节若§≥1认为是两个惯性环节
七、延迟环节（又称纯滞后环节）
τ0：纯延迟时间
在延迟时间很小的情况下，延迟环节可用一个小惯性环节来代替。
第2章 2-4 典型环节分析.
12
下图给出了微分环节的实例。
在图(a)的电路中，输出电压uc与输入电压ur间的微分方程为：
传递函数为： 式中：
13
在图 (b) 中，输出电流 i(t) 与输入电压ur (t) 间的微分方程为：
式中
其传递函数为：
14
在图 (c) 中，选取直流测速发电机的输入量为转角θ， 输出量为电枢电压 u(t) 则其输入、输出间的微分方程为
2.4、典型环节的分析
一个物理系统是由许多元件组合而成的，虽然元件的 结构和作用原理多种多样，但若考察其数学模型，却可 以划分成为数不多的几种基本类型，称之为典型环节。 这些环节是比例环节、惯性环节、积分环节、振荡环 节、微分环节和滞后环节 1.比例环节比例环节又称放大环节。 其数学方程为：
式中c(t)为输出量，r(t)为输入量，K为放大系数（或增益）。
16
上述各典型环节，是从数学模型的角度来划分 的。 它们是系统传递函数的最基本的构成因子。 在和实际 元件相联系时，应注意以下几点： ⑴系统的典型环节是按数学模型的共性来划分 的，他与 系统中使用的元件并非都是一一对应的，一 个元件的数 学模型可能是若干个典型环节的数学模型的组合。而若 干个元件的数学模型的组合也可能就是一个典型的数学 模型。 ⑵同一装置（元件），如果选取的输入、输出量不同， 它可以成为不同的典型环节。如直流电动机 以电枢电压 为输入、转速为输出时，它是一个二阶振 荡环节。但若 以电枢电流为输入、转速为输出时，它却是一个积分环 节。
17
⑶在分析和设计系统时，将被控对象（或系统）的数学模 型进行分解，就可以了解它是由哪些典型环 节所组成的。 因而，掌握典型环节的动态特性将有助于对系统动态特性 的分析研究。 ⑷ 典型环节的概念只适用于能够用线性定常数学模型描述 的系统。 既然可以把组成控制系统的元件划分为若干典型环节， 那么控制系统的传递函数也可以写成如下一般形式：
下图给出了微分环节的实例。
在图(a)的电路中，输出电压uc与输入电压ur间的微分方程为：
传递函数为： 式中：
13
在图 (b) 中，输出电流 i(t) 与输入电压ur (t) 间的微分方程为：
式中
其传递函数为：
14
在图 (c) 中，选取直流测速发电机的输入量为转角θ， 输出量为电枢电压 u(t) 则其输入、输出间的微分方程为
2.4、典型环节的分析
一个物理系统是由许多元件组合而成的，虽然元件的 结构和作用原理多种多样，但若考察其数学模型，却可 以划分成为数不多的几种基本类型，称之为典型环节。 这些环节是比例环节、惯性环节、积分环节、振荡环 节、微分环节和滞后环节 1.比例环节比例环节又称放大环节。 其数学方程为：
式中c(t)为输出量，r(t)为输入量，K为放大系数（或增益）。
16
上述各典型环节，是从数学模型的角度来划分 的。 它们是系统传递函数的最基本的构成因子。 在和实际 元件相联系时，应注意以下几点： ⑴系统的典型环节是按数学模型的共性来划分 的，他与 系统中使用的元件并非都是一一对应的，一 个元件的数 学模型可能是若干个典型环节的数学模型的组合。而若 干个元件的数学模型的组合也可能就是一个典型的数学 模型。 ⑵同一装置（元件），如果选取的输入、输出量不同， 它可以成为不同的典型环节。如直流电动机 以电枢电压 为输入、转速为输出时，它是一个二阶振 荡环节。但若 以电枢电流为输入、转速为输出时，它却是一个积分环 节。
17
⑶在分析和设计系统时，将被控对象（或系统）的数学模 型进行分解，就可以了解它是由哪些典型环 节所组成的。 因而，掌握典型环节的动态特性将有助于对系统动态特性 的分析研究。 ⑷ 典型环节的概念只适用于能够用线性定常数学模型描述 的系统。 既然可以把组成控制系统的元件划分为若干典型环节， 那么控制系统的传递函数也可以写成如下一般形式：
第二章 控制系统的数学模型
⇒
QQQr00(((sss)))−−=QQH0c1(((sss)))R=−=1Hcc122s(sHsH)12(s()s)
qc (t)
=
h2 (t) R2
Qc
(s)
=
H2 (s) R2
G(s)
=
Qc (s) Qr (s)
=
R1R 2C1C 2s 2
1 + (R1C1 + R2C2
机理分析法：
依据描述系统运动规律的定律并通过理论推导 来得到数学模型的方法 。
实验辨识法：
通过整理基于系统输入－输出的实验数据来 得到系统的数学模型。本章着重讨论机理分析 法。
建模特点：相似性、简化性、准确性。
数学模型类型： 经典控制理论: 微分方程（连续系统）、
差分方程（离散系统） 、传递函数、系 统方框图和信号流图； 现代控制理论：状态方程
注：如果在第(3)步结束时已经得到符合第(4)步要求的微分方程，则 无须第(4)步。
线性定常系统微分方程的一般形式
an
d nc(t) dt n
+
an−1
d n−1c(t ) dt n−1
+
...
+
a1
dc(t ) dt
+
a0c(t )
=
bm
d mr(t) dt m
+
bm −1
d m−1r(t ) dt m−1
d x(t ) + dt
Kx(t ) = f (t )
当f(t)=f1(t)时，上述方程的解为x1(t)； 当f(t)=f2(t)时，上述方程的解为x2(t)； 如果f(t)=f1(t)+ f2(t) ,方程的解为x(t)= x1(t)+x2(t),这就是叠加性
第二章 典型环节的数学模型(2-1)
18
电机运动方程
1） T(t)=Ki(t) 2） e (t) K d (t)
b b
dt
T(t)——转矩 K——力矩系数 eb(t)——反电势 Kb——反电势常数 ea(t)——电枢两端的电压
i a (t )
R
3） L di(t) Ri(t) e (t) e (t) b a
dt
4）
2
传递函数：
R(s)
1 T 2 s 2 2 Ts 1
C ( s)
式中：——阻尼比， T——振荡环节的时间常数。 频率特性： C ( j ) 1
G ( j ) R ( j ) (1 T 2 2 ) j 2 T
16
R
L
+
i (t )
+
例：RLC电路
r(t)
_
C
传递函数：
I(s) s 1 （R=1 U(s)
RC= ）
频率特性：
G jω 1 jω
一阶微分环节可看成一个微分环节与一个比例环节 的并联，其传递函数和频率特性是惯性环节的倒数。
24
7、二阶微分环节
特点：输出量与输入量及输入量的一阶、二阶导数都有关 运动方程： 2
d r(t ) dr(t ) c(t ) T 2ζ T r(t ) 2 dt dt
+ _
D
J
B
19
消去中间变量Eb(s)、T(s)和I(s)
θ (s) K E a (s) s[LJs2 (LB RJ)s (RB KK b )]
如果输入量Ea(s)，输出量转速(s)，则又可得到：
(s) K E a (s) LJs 2 (LB RJ)s (RB KK b )
电机运动方程
1） T(t)=Ki(t) 2） e (t) K d (t)
b b
dt
T(t)——转矩 K——力矩系数 eb(t)——反电势 Kb——反电势常数 ea(t)——电枢两端的电压
i a (t )
R
3） L di(t) Ri(t) e (t) e (t) b a
dt
4）
2
传递函数：
R(s)
1 T 2 s 2 2 Ts 1
C ( s)
式中：——阻尼比， T——振荡环节的时间常数。 频率特性： C ( j ) 1
G ( j ) R ( j ) (1 T 2 2 ) j 2 T
16
R
L
+
i (t )
+
例：RLC电路
r(t)
_
C
传递函数：
I(s) s 1 （R=1 U(s)
RC= ）
频率特性：
G jω 1 jω
一阶微分环节可看成一个微分环节与一个比例环节 的并联，其传递函数和频率特性是惯性环节的倒数。
24
7、二阶微分环节
特点：输出量与输入量及输入量的一阶、二阶导数都有关 运动方程： 2
d r(t ) dr(t ) c(t ) T 2ζ T r(t ) 2 dt dt
+ _
D
J
B
19
消去中间变量Eb(s)、T(s)和I(s)
θ (s) K E a (s) s[LJs2 (LB RJ)s (RB KK b )]
如果输入量Ea(s)，输出量转速(s)，则又可得到：
(s) K E a (s) LJs 2 (LB RJ)s (RB KK b )
第二章：控制系统的数学模型
第二章控制系统的数学模型本章目录2.1 传递函数2.2 传递函数的说明2.3 非线性数学模型的线性化2.4 典型环节的传递函数数学模型2.5 用方块图表示的模型2.6 信号流程图与梅逊公式2.7* 数学模型的MATLAB描述小结本章简介系统是指相互联系又相互作用着的对象之间的有机组合。
许多控制系统，不管它们是机械的、电气的、热力的、液压的，还是经济学的、生物学的等等，都可以用微分方程加以描述。
如果对这些微分方程求解，就可以获得控制系统对输入量（或称作用函数）的响应。
系统的微分方程，可以通过支配着具体系统的物理学定律，例如机械系统中的牛顿定律，电系统中的克希霍夫定律等获得。
为了设计（或者分析）一个控制系统，首先需要建立它的数学模型，即描述这一系统运动规律的数学表达式。
有三种比较常用的描述方法：一种是把系统的输出量与输入量之间的关系用数学方式表达出来，称之为输入--输出描述，或外部描述，例如微分方程式、传递函数和差分方程。
第二种不仅可以描述系统的输入、输出间关系，而且还可以描述系统的内部特性，称之为状态变量描述，或内部描述，它特别适用于多输入、多输出系统，也适用于时变系统、非线性系统和随机控制系统。
另一种方式是用比较直观的方块图模型来进行描述。
同一控制系统的数学模型可以表示为不同的形式，需要根据不同情况对这些模型进行取舍，以利于对控制系统进行有效的分析。
本章所讨论的数学模型以传递函数和方块图为主。
2.1 传递函数在控制理论中，为了描述线性定常系统的输入-输出关系，最常用的函数是所谓的传递函数。
传递函数的概念只适用于线性定常系统，在某些特定条件下也可以扩充到一定的非线性系统中去。
线性定常系统的传递函数，定义初始条件为零时，输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。
设有一线性定常系统，它的微分方程是(2-1)式中y是系统的输出量，x是系统的输入量。
初始条件为零时，对方程（2-1）两端进行拉普拉斯变换，就可以得到该系统的传递函数为：(2-2)传递函数是一种以系统参数表示的线性定常系统的输入量与输出量之间的关系式，它表达了系统本身的特性，而与输入量无关。
自动控制理论 2-1 控制系统的数学模型
i (t ) =
uc (t ) R
运动方程： 运动方程： 传递函数： 传递函数：
u r (t) =
G(s) =
1 RC
∫u
c
(t)dt + u c (t)
U c (s) Tc s = U r (s) Tc s + 1
（Tc=RC）
G(s) = U c (s) = Tc s U r (s)
当Tc<<1时，又可表示成：
传递函数
36
例：直流电机
输入量: ud ——电枢电压 输出量： id ——电枢电流 动态方程如下：
第二章 控制系统的数学模型
第二次课 1
1.引言
系统的数学模型：描述系统输入、输出变量以及内部其他变 量之间关系的数学表达式。 控制系统中常见的二种数学模型形式： 1、外部描述：把系统的输出量与输入量之间的关系用数 外部描述：把系统的输出量与输入量之间的关系用数 学方式表达出来，称之为输入— 学方式表达出来，称之为输入—输出描述，或外部描述， 例如微分方程、传递函数、框图和差分方程。适用于单输 例如微分方程、传递函数、框图和差分方程。适用于单输 入、单输出系统。
L C
u r(t)
2
uc(t)
d uc du c LC + RC + uc = ur 2 dt dt
二阶微分方程
9
例2-3 阻尼器系统 (P15)
d 2 y (t ) dy (t ) m + f + ky (t ) = F (t ) 二阶微分方程 2 dt dt
10
本节重点：
控制系统微分方程的建立的方法 两种典型控制系统微分方程的建立。 两种典型控制系统微分方程的建立
第2章 数学模型
35
3. R ( s ) 作用下的误差传递函数
E ( s) 1 e (s) R( s) 1 G1 ( s)G2 ( s ) H ( s )
4. N ( s) 作用下的误差传递函数
G2 ( s) H ( s) E ( s) en ( s) N (s) 1 G1 ( s)G2 ( s) H ( s)
n
例2-7 原理图
例2-7 结构图
26
2.3.2 结构图的等效变换及化简
结构图等效变换的两条基本原则是： 1）变换前后前向通道中传递函数的乘积应保持不变；
2）变换前后各回路中传递函数的乘积应保持不变。
1. 基本连接的等效变换
结构图的基本连接方式有三种：串联、并联和反馈。 （1）串联
27
（2）并联
就可以近似地认为ｅ是沿着Ａ点上的切线
（直线）变化，这就是将非线性特性线性 化的方法，也称为小偏差法。
5
将非线性函数ｙ＝ｆ（ｘ）在工作点（ｘ０，ｙ ０）处展开成泰勒级数:
当忽略二次及二次以上的高次项时，就得到了一 个线性方程式：
线性化增量方程： y Kx
6
2.1.3 线性微分方程的求解
线性微分方程的求解，拉氏变换法： 拉氏变换法求解微分方程步骤： （1）方程两边求拉氏变换。 （2）给定的初始条件代入方程。 （3）求出系统输出量的拉式变换式。 （4）拉式反变换求出系统输出的时间解。
对于电路网络，可利用复阻抗的概念，直接写出 拉氏变换关系的代数方程求解传递函数。
电路网络中 的复阻抗：
电阻 —— R 电感 —— Ls
1 电容 —— Cs
20
例2-5 试求图2-11 所示有源电路网络的传递函数。
第二章part-II典型环节结构图梅森公式wmx
因为v2 v1 0， 所以K 趋向于无穷大。
输出 反相输入 同相输入
补充例4 倒相放大器
解：∵在理想情况下，
i1 0
v2 v1
∴关于节点 v1 的节点方程为：
v1 vin v1 v0 0 R1 R2
输入电流＝输出电流
v2 0
v1 v2 0
vin v0 0 R1 R2 即 v0 R 2 vin R1
G(S ) G1 (S ) G2 (S ) .... Gn (S )
(3)反馈回路传递函数的求取 前向通道：由偏差信号至输出信号的通道； 反馈通道：由输出信号至反馈信号的通道。
Y (S ) G(S ) E (S ) E (S) X(S) - F(S) F(S) H(S)Y(S)
从节点方程中可以得到：
在特殊的情况下， 如果：R2 R1 ， 则：v0 vin 这时，图中的倒相放大器只起到反相的作用。
解： 输入电压与输出电压间的关系为：
按传递函数的定义，可以得到
从图2.11中可以看出，比例环节的特点是：输出信号y(t)和输入信号
x(t)的形状相同。只是比例环节将原信号放大了K倍。
U y ( s)
惯性环节的阶跃响应曲线是 一条指数函数的上升曲线。 从图中可以看出在初始时， 速度的变化最大
惯性环节的阶跃响应曲线
惯性环节的动态方程为一阶微分方程： 将阶跃函数输入 代入方程，求解得到：
y(t ) Kx0 (1 et / T )
在t＝0时刻，初始上升速度为：
Kx0 t / T dy y (0) e dx t 0 T
几个基本概念及术语
R(s)
N(s)
+ -
控制系统的数学模型
第二章控制系统的数学模型2-1 什么是系统的数学模型？大致可以分为哪些类型？答定量地表达系统各变量之间关系的表达式，称工矿企业数学模型。
从不同的角度，可以对数学模型进行大致的分类，例如：用来描述各变量间动态关系的数学模型为动态模型，用来描述各变量间稳态关系有数学模型为静态模型；数学模型中各变量与几何位置无关的称为集中参数模型，反之与几何位置有关的称为分布参数模型；变量间关系表现为线性的称为线性模型，反之非线性模型；模型参数与时间有关的称为时变模型，与时间无关的称为时不变或定常模型；以系统的输入、输出变量这种外部特征来描述系统特性的数学模型称为输入输出模型，而以系统内部状态变量描述的数学模型称为状态空间模型；等等。
2-2 系统数学模型的获取有哪几种方法？答获取系统数学模型的方法主要有机理分析法和实验测试法。
机理分析法是通过对系统内部机理的分析，根据一些基本的物理或化学变化的规律而导出支配系统运动规律的数学模型，这样得到的模型称为机理模型。
实验测试法是通过对实际系统的实验测试，然后根据测试数据，经过一定的数据处理而获得系统的数学模型，这样得到的模型可称为实测模型或经验模型。
如果将上述两种方法结合起来，即通过机理分析的方法预先得到数学模型的结构或函数形式，然后对其中的某些参数用实验辨识的方法来确定，这样得到的数学模型可称为混合模型。
这是介于上述两种方法之间的一种比较切合实际的应用较为普遍的方法。
2-3 通过机理分析法建立对象微分方程数学模型的主要步骤有哪些？答主要步骤有：⑴根据系统的控制方案和对象的特性，确定对象的输入变量和输出变量。
一般来说，对象的输出变量为系统的被控变量，输入变量为作用于对象的操纵变量或干扰变量。
⑵根据对象的工艺机理，进行合理的假设和简化，突出主要因素，忽略次要因素。
⑶根据对象的工艺机理，从基本的物理、化学等定律出了，列写描述对象运动规律的原始微分方程式（或方程式组）。
⑷消去中间变量，推导出描述对象输入变量与输出变量之间关系的方程式。
自动控制原理-控制系统的数学模型可编辑全文
23
r(t)
b1
d m1 dt m1
r(t)
bm1
d dt
r(t)
bm r (t )
c(t)是系统输出量，r(t)是系统输入量，参数是常系数。
性质：满足叠加原理
6
3. 系统微分方程的建立步骤
第一步：将系统分成若干个环节，列写各环节的 输出输入的数学表达式。
利用适当物理定律—如牛顿定律、 基尔霍夫定律、能量守恒定律等。
s2 2
n 1 2
e nt
s in( n
1 2t)
n2 s 2 2n s n 2
12
4、拉氏反变换
查表实现
f
(t )
1 2pj
s j F ( s )e st ds
s j
F(s)化成下列因式分解形式：
F (s) B(s) k(s z1)(s z2 ) (s zm ) A(s) (s s1)(s s2 ) (s sn )
设双变量非线性方程为：y f (x1，, x工2 ) 作点为
则可近似为：
y K1x1 K2x2
y0 f (x10 , x20 )
x1 x1 x10 x2 x2 x20
K1
y x1
| , K x1x10
2
x2 x20
y x2
|x1 x10
x2 x20
[注意]： ⑴上述非线性环节不是指典型的非线性特性（如间隙、饱和特 性等），它可以用泰勒级数展开。 ⑵实际的工作情况在工作点附近。 ⑶变量的变化必须是小范围的。其近似程度与工作点附近的非 线性情况及变量变化范围有关。
◆F(s)中具有单极点时，可展开为
F (s) c1 c2 cn
s s1 s s2
s sn
r(t)
b1
d m1 dt m1
r(t)
bm1
d dt
r(t)
bm r (t )
c(t)是系统输出量，r(t)是系统输入量，参数是常系数。
性质：满足叠加原理
6
3. 系统微分方程的建立步骤
第一步：将系统分成若干个环节，列写各环节的 输出输入的数学表达式。
利用适当物理定律—如牛顿定律、 基尔霍夫定律、能量守恒定律等。
s2 2
n 1 2
e nt
s in( n
1 2t)
n2 s 2 2n s n 2
12
4、拉氏反变换
查表实现
f
(t )
1 2pj
s j F ( s )e st ds
s j
F(s)化成下列因式分解形式：
F (s) B(s) k(s z1)(s z2 ) (s zm ) A(s) (s s1)(s s2 ) (s sn )
设双变量非线性方程为：y f (x1，, x工2 ) 作点为
则可近似为：
y K1x1 K2x2
y0 f (x10 , x20 )
x1 x1 x10 x2 x2 x20
K1
y x1
| , K x1x10
2
x2 x20
y x2
|x1 x10
x2 x20
[注意]： ⑴上述非线性环节不是指典型的非线性特性（如间隙、饱和特 性等），它可以用泰勒级数展开。 ⑵实际的工作情况在工作点附近。 ⑶变量的变化必须是小范围的。其近似程度与工作点附近的非 线性情况及变量变化范围有关。
◆F(s)中具有单极点时，可展开为
F (s) c1 c2 cn
s s1 s s2
s sn
自动控制理论第二章--线性系统的数学模型全
理
论 一.物理模型 、数学模型及数学建模
物理模型 ：
任何元件或系统实际上都是很复杂的，难以对
它作出精确、全面的描述，必须进行简化或理想化。
简化后的元件或系统称为该元件或系统的物理模型。
简化是有条件的，要根据问题的性质和求解的精确
要求来确定出合理的物理模型。
2
第二章 线性系统的数学模型
自
动
控
制 理
物理模型的数学描述。是指描述系统
零初使条件是指当t≤0时,系统r(t)、c(t)以及它们的各阶
导数均为零。
传递函数
输出信号的拉氏变换 输入信号的拉氏变换
零初始条件
C(s) R(s)
26
第二章 线性系统的数学模型
自
动
控 线性系统微分方程的一般形式为:
制
理 论
制 理 论
F(s)
br (s p1)r
br 1 (s p1)r1
b1 (s p1)
ar 1 s pr1
an s pn
br
B(s)
A(s)
(s
p1
)r
s p1
br 1
d
ds
B(s) A(s)
(s
p1 ) r
s p1
br j
1 dj
j!
ds
j
B(s) A(s)
(s
p1
La
dia (t ) dt
Raia (t )
Ea
+
(1) -
La
if Ra
m
+ ia
Ea ——电枢反电势，其表达式为 Ua
Ea S M
负 载
jmfm
Ea Cem(t) (2) --
第二章(典型环节和方框图的等效变换)
方框图的组成要素
1信号线 带有箭头的直线，箭头表示信号的
传递方向，直线旁标记信号的时间函 数或象函数。
2信号引出点（线）/测量点 表示信号引出或测量的位置和传递方向。同一信号线上引出的信号，
其性质、大小完全一样。
二、方框图的组成和建立
1. 由四种基本图形符号组成。
（1）函数方块 (2) 信号线
R(s) r(t) G(s)
R(s)
r(t)
C(s) c(t)
R(s) R(s)
(3) 分支点(引出点)
r(t) r(t) R(s)
r(t)
（4)综合点(比较点或相加点)
R(s)
R(s)±B(s)
r(t) ± r(t)±b(t)
B(s) b(t)
(1)函数块（传递方框）：方框内为具体环 节的传递函数。
(2)信号线： 表示输入、输出通道，箭头代 表信号的传递方向。
(3)信号相加点（综合点、比较点）：表示 几个信号相加减。
(4)信号分支点（引出点）：表示同一信号 输出到几个地方。
2 系统方框图的绘制 系统方框图的绘制步骤如下： (1)根据信号传递过程，将系统划分为若干
个环节或部件。 (2)确定各环节的输入量与输出量，求出各
环节的传递函数。 (3)绘出各环节的方框图。 (4)将各环节相同的量依次连接，得到系统
G2(s)
E(s) G1(s)
N(s)=0时系统的等效图
c(t) d 1(t) (t)
dt
几个实际微分的例子
C
i
u(t)
R
y(t)
RC串联电路
Y (s) R RCs U (s) 1 sC R RCs 1
G(s) Y(s) s U (s) s 1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
T2
d 2c(t) dt2
2ζT
dc(t) dt
c(t)
Kr(t)
传递函数：
R(s)
1
C(s)
T 2s2 2 Ts 1
式中：——阻尼比， T——振荡环节的时间常数。
频率特性：
G( j ) C( j )
1
R( j ) (1 T 2 2 ) j2 T
16
例：RLC电路
R
L
+
r(t)
i(t)
C
G(s) K s
频率特性：
G(jω ) K jω
10
例：积分电路
输入为r(t)，输出为c(t)
ic (t) C
i1(t ) R1
-
+K
r (t )
c (t )
R3
ic (t)
i1 (t)
r(t) R1
R(s)
1
R1Cs
C(s)
运动方程：
传递函数：
c(t)
1 C
ic (t)dt
1 R1C
19
消去中间变量Eb(s)、T(s)和I(s)
θ (s) Ea (s)
s[LJs 2
K (LB RJ)s (RB KK b )]
如果输入量Ea(s)，输出量转速(s)，则又可得到：
(s)
K
Ea (s) LJs2 (LB RJ)s (RB KK b )
这是一个典型的振荡环节的传递函数
dt
式中：K——弹簧弹性系数；
M——物体的质量，
B——粘性摩擦系数。
传递函数：
1
G(s) X(s)
K
F(s) M s2 B s 1
KK
K f (t)
M x(t)
B 图2-16 机械振荡
22
6、一阶微分环节
特 点：此环节的输出量不仅与输入量本身 有关，而且与输入量的变化率有关
运动方程： c(t) T dr(t) r(t) dt
第二章 物理系统的数学模型
第一节 控制工程的数学方法 （Laplace变换）
第二节 物理系统的数学模型 第三节 非线性数学模型的线性化
1
第四节 典型环节及其传递函数
1、比例环节（又叫放大环节）
R(s)
特 点：输出量按一定比例复现输入量， 无滞后、失真现象。
C(s)
K
运动方程 : c(t)=Kr(t) K——放大系数，通常都是有量纲的。
r(t)dt
1 T
r(t)dt
G(s) C(s) 1 K R(s) Ts s
（T=R1C）
频率特性： G(j ) C(j ) K
R(j ) jT
11
其它举例
n(t) D
x (t )
N (s)
D
X (s)
s
i (t ) u(t)
I (s)
1
U (s)
Cs
12
4、惯性环节(又叫非周期环节)
频率特性：
(jω )
K
Ea (jω ) (RB KK b - LJω2 ) j(LB RJ)ω
20
电枢回路中的电感L通常较小，若忽略L的影响，则：
θ (s)
Km
Ea (s) s(Tms 1)
(s)
Km
Ea (s) Tms 1
式中：km=K/(RB+KKb) ——电动机增益常数 Tm=RJ/(RB+KKb)——电动机时间常数。
特 点：动态过程中，输出量正比于输入量的变化速度。
R(s)
S
C(s)
运动方程：
C(t) K dr(t) dt
传递函数： 频率特性：
G(s) C(s) KS R(s)
G(jω ) C(jω ) jKω R(jω )
6
例 RC电路
ur (t)
i (t )
C
R
uc (t)
设：输入——ur(t) 输出——uc(t)
Ld
d dt
id
Rd id
ud
即
d
d dt
id
ud Rd
+
d
Ld Rd
ud
传递函数:
1 G(s) Id (s) Rd
Ud (s) ds 1
式中 Ld ——电枢回路电感； Rd ——电枢回路电阻； τd ——电枢绕组的时间常数；
id D
14
其他一些例子
L
r(t)
R c(t)
R(s)
1
C(s)
R
dt
dt
传递函数：
I(s) s 1 （R=1
U(s)
RC= ）
频率特性： Gjω 1 jω
一阶微分环节可看成一个微分环节与一个比例环节 的并联，其传递函数和频率特性是惯性环节的倒数。
24
7、二阶微分环节
特点：输出量与输入量及输入量的一阶、二阶导数都有关
运动方程：
c(t)
T2
d 2 r(t) dt 2
频率特性： G（j）=K
3
例：输入：n1(t)——转速 输出：n2(t)——转速
Z1
n1 (t )
n2 (t) Z2
Z1——主动轮的齿数 Z2——从动轮的齿数
N1 s
z1
N2 s
z2
运动方程： 传递函数：
n 2 (t)
z1 z2
n1 (t)
G(s) N 2 (s) z1 K N1(s) z 2
传递函数： G(s) C(s) K
R(s)
C(j )
频率特性：
G(j )
K
R(j )
2
例： 输入：(t)——角度 输出：u(t)——电压
E——恒定电压
+ E
-
u(t)
+
(t) •
(s)
U (s)
K
运动方程： u(t)=K(t) 传递函数： G(s) U(s) K
(s)
K——比例系数，量纲为伏/弧度。
特点：此环节中含有一个独立的储能元件，以致对突变的输 入来说，输出不能立即复现，存在时间上的延迟。
R(s)
1
C(s)
Ts 1
运动方程： T dc(t) c(t) Kr(t)
dt
传递函数： 频率特性：
G(s) K Ts 1
G(jω ) K jTω 1
13
例：直流电机
输入量: ud ——电枢电压 输出量： id ——电枢电流 动态方程如下：
8
其他举例
i(t) C uc (t)
U c (s)
I (s)
Cs
i(t) C
u(t)
R
U (s)
Cs
+ I(s)
1
+
R
i (t )
L
eL (t)
I (s)
EL (s)
Ls9ຫໍສະໝຸດ 3、积分环节特点：输出量的变化速度和输入量成正比。
R(s)
1
C(s)
s
运动方程： dc(t) Kr(t )
dt
传递函数：
例如：前面介绍的振荡环节中两个例子，一个是机械系统， 另一个是电气系统，但传递函数的形式完全相同。
（2）同一个系统，当我们选取不同的输入量、输出 量 时，就可能得到不同形式的传递函数。
例如：电容：输入—电流，输出—电压，则是积分环节。 反之，输入—电压，输出—电流，则为微分环节。
26
频率特性：
G(jω ) N2 (jω ) z1 K N1(jω ) z2
4
其它一些比例环节
R2
R1 -
r (t )
r1
r2
r (t )
c (t )
+K
c (t ) R3
+ Ec
R
ic (t)
ib (t)
R(s)
r2
Cs
r1 r2
R(s)
R2
R1
Cs
Ib (s)
Ic (s)
5
2、微分环节
L
dt 2
dt
eb (t) (t)
分别进行拉氏变换
ea (t)
+ _
D
J
B
1） T ( s ) = K I ( s )
_
2） Eb( s ) = Kb s ( s ) 3） Ea( s ) = ( L s + R ) I ( s ) + Eb( s ) 4） T( s ) = ( J s2 + B s ) ( s )
2ζT
dr(t) dt
r(t)
传递函数： G(s) C(s) T2s2 2ζTs 1
R(s)
频率特性： G( j ) T 2 ( j )2 2 T ( j ) 1
(1 T 2 2 ) j2 T
可以看出，二阶微分环节的传递函数和频率特性是振荡环 节的倒数。
25
小结
（1）不同物理性质的系统，可以有相同形式的传 递函数。
u r
(t)
1 c
i(t)dt i(t)R
i(t) uc (t) R
消去i(t)，得到运动方程：
ur (t)
1 RC
uc (t)dt uc (t)
传递函数： G(s) Uc (s) Tcs
U r (s) Tcs 1
（Tc=RC）
当Tc<<1时，传递函数又可表示成： G(s)
Uc (s) U r (s)
传递函数： G( s ) = Ts + 1 频率特性： G( j ) = j T + 1
23
RC电路
i1(t) C