勾股定理及两点间距离公式C(教师版)
- 格式:doc
- 大小:5.45 MB
- 文档页数:15


平面坐标2点之间距离公式在平面直角坐标系中,我们经常需要计算两个点之间的距离。
这个距离可以用一个简单的公式来计算,即两点间距离公式。
本文将介绍如何使用该公式来计算平面坐标系中两点之间的距离。
1. 坐标系简介平面直角坐标系是一个由两条垂直的坐标轴组成的二维坐标系。
其中,横轴称为x轴,纵轴称为y轴。
任意一点在坐标系中可以用一个有序数对(x, y)表示,其中x是该点在x轴上的坐标,y是该点在y轴上的坐标。
2. 两点间距离公式设平面上有两点A(x1, y1)和B(x2, y2),我们需要计算这两点之间的距离。
根据勾股定理,两点之间的直线距离可以表示为:距离= √((x2 - x1)² + (y2 - y1)²)其中,√表示开平方根,(x2 - x1)²表示x坐标差的平方,(y2 - y1)²表示y 坐标差的平方。
3. 实例演示假设有两点A(3, 4)和B(-2, -1),我们将演示如何使用上述公式计算它们之间的距离。
根据公式,我们可以计算出:距离= √((-2 - 3)² + (-1 - 4)²)= √((-5)² + (-5)²)= √(25 + 25)= √50≈ 7.07所以,点A和点B之间的距离约为7.07个单位。
4. 总结通过上述实例演示,我们可以看到,在平面直角坐标系中,计算两点之间的距离可以使用距离公式。
这个公式简单直观,只需要计算两点的坐标差的平方和,然后将其开平方根即可得到两点之间的距离。
在实际应用中,这个公式可以用于测量两个平面坐标点之间的距离,以及计算线段或多边形的长度等。
它在几何学、物理学、计算机图形学等领域都有广泛的应用。
希望本文能够帮助你理解平面坐标系中两点之间距离的计算方法,并能够应用于实际问题的解决中。



初二上勾股定理(经典题型)数学秋季班教案第十九章几何证明——勾股定理及两点之间的距离公式知识回顾】勾股定理是指对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有a²+b²=c²(直角三角形两直角边的平方和等于斜边的平方)。
勾股定理的逆定理是指如果三角形的三边长a、b、c有关系,a²+b²=c²,那么这个三角形是直角三角形。
常见的勾股数有(3n,4n,5n)、(5n,12n,13n)、(8n,15n,17n)、(7n,24n,25n)、(9n,40n,41n)等。
勾股定理的证明图如下:两点之间的距离公式是AB = √[(x₂-x₁)²+(y₂-y₁)²]。
例题讲解】例题1:已知a₁=1,a₂=5,a₃=13,a₄=25,a₅=41,a₆=61.aₙ=aₙ₋₂+aₙ₋₃,求a₇。
解析:根据题意,a₇=a₅+a₄=66.例题2:如图所示,已知△ABC的三边AB=15,BC=20,AC=25,求△ABC最长边上的高。
解析:根据海伦公式,可得△ABC的面积为150,再根据最长边上的高公式,可得最长边上的高为12.例题4:已知如图△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF²=BE²+FC².解析:根据勾股定理,可得BE²=AB²-AE²,FC²=AC²-AF²,代入EF²=BE²+FC²中得证。
例题6:一只2.5m长的梯子斜靠在一竖直的墙上,这时梯脚距离墙角0.7m,如果梯子的顶端沿墙下滑0.4m,那么梯脚移动的距离是多少?解析:根据勾股定理,可得梯子顶端到地面的距离为√(2.5²-0.7²-0.4²)=2.31m,因此梯脚移动的距离为2.31-0.7=1.61m。


解析几何中两点间距离公式欢迎来到解析几何的世界。
你是否曾经在求两点间距离时使用过勾股定理?如果这还是你的唯一方法,那么我建议你应该试试使用解析几何中的公式来求解两点间的距离。
在此,我将会向你介绍两点距离公式以及它的相关内容。
让我们开始吧!一、什么是两点间距离公式?两点间距离公式,是解析几何中用于计算两个点之间距离的公式。
它可以用于二维平面和三维空间中。
在二维平面中,两点间距离公式被表示为:d = √ ((x2 - x1)² + (y2 - y1)²)其中,d为两点之间的距离,(x1, y1)和(x2, y2)是平面上的两个点。
在三维空间中,两点间距离公式被表示为:d = √ ((x2 - x1)² + (y2 - y1)² + (z2 - z1)²)其中,d为两点之间的距离,(x1, y1, z1)和(x2, y2, z2)是空间中的两个点。
二、两点间距离公式的推导过程在计算两点间距离公式的推导过程中,我们使用了勾股定理(两边平方,然后开方),从而得到了该公式。
我们将在下面详细讲解推导过程。
二维平面:为了推导两点间距离公式,在平面上我们假设有两个点A和B。
如下图所示:我们可以通过画一个直角三角形来计算AB之间的距离。
我们可以看出,点A和点B之间的距离等于C点到直角三角形的对角线长度。
如下图所示:根据勾股定理,我们可以得出方程:C² = A² + B²其中,C为对角线的长度,A和B为直角三角形两条边的长度。
将上述方程稍加变换后,可以得出两点之间的距离公式:d = √ ((x2 - x1)² + (y2 - y1)²)三维空间:在三维空间中,我们同样假设有两个点A和B。
与二维平面的情况类似,我们可以通过画一个直角三角形来计算AB之间的距离。
如下图所示,假设我们要计算点A和点B之间的距离。
我们可以通过勾股定理来计算AB之间的距离。

模块一:勾股定理的证明及应用知识精讲1、勾股定理:(1)直角三角形中,两条直角边的平方和,等于斜边的平方.利用勾股定理往往构造方程,已达到解决问题的目的;(2)应用勾股定理解决实际问题,要注意分析题目的条件,关注其中是否存在直角三角形,如果存在直角三角形,根据所给的三边条件,建立方程,从而解决问题;如果问题中没有直角三角形,可以通过添加辅助线构造出直角三角形,寻求等量关系,再根据勾股定理建立相应的方程,因此,在解决直角三角形中有关边长的问题时,要灵活的运用方程的思想.例题解析【例1】(1)在直角△ABC中,∠C=90°,∠A=30°,BC=1,则AB=_________;(2)在直角△ABC中,∠C=90°,∠A=45°,AB=3,则AC=_________.【例2】(1)等边三角形的边长是3,则此三角形的面积是___________;(2)等腰三角形底边上的长为2,腰长为4,则它底边上的高为__________.【例3】(1)直角三角形两边长为3和4,则此三角形第三边长为_________;(2)直角三角形两直角边长为3和4,则此三角形斜边上的高为_________;(3)等腰三角形两边长是2、4,则它腰上的高是____________.【例4】(1)若直角三角形的三边长分别为N+1,N+2,N+3则N的值是____________;(2)如果直角三角形的三边长为连续偶数,则此三角形的周长为______________.【例5】 如图,在直角△ABC 中,∠ACB =90°,∠B=60°,D 是斜边AB 的中点,BC =2,求△ADC 的周长.【例6】 如图,已知:R t △ABC 中,∠ACB 是直角,BC =15,AB 比AC 大9,CD ⊥AB 于点D ,求CD 的长.【例7】 已知已直角三角形的周长为4+26,斜边上的中线为2,求这个直角三角形的面积.【例8】 如图,直线MN 是沿南北方向的一条公路,某施工队在公路的点A 测得北偏西30°的方向上有一栋别墅C ,朝正北方向走了400米到达点B 后,测得别墅C 在北偏西75°的方向上,如果要从别墅C 修一条通向MN 的最短小路,请你求出这条小路的长(结果保留根号).A BCD A BCM MNBC D【例9】 如图,公路MN 和公里PQ 在点P 处交汇,且∠QPN =30°,点A 处有一所中学,AP =160米,假设拖拉机行驶时,周围100米以内会受到噪音的影响,那么拖拉机在MN 上沿PN 方向行驶时,学校是否会受到噪音的影响?请说明理由;如果受影响,已知拖拉机的速度是18千米/时,那么学校受影响的时间是多少秒?【例10】 如图,矩形ABCD 中,AB =8,BC =4,将矩形沿AC 进行翻折,点D 落在E 处,求出重叠部分△AFC 的面积.【例11】 如图,AB 两个村子在河边CD 的同侧,A 、B 两村到河边的距离分别为AC =1千米,BD =3千米,CD =3千米.现在河边CD 建一座水厂,建成后的水厂,可以直接向A 、B 两村送水,也可以将水送一村再转送另一村.铺设水管费用为每千米2万元,试在河边CD 选择水厂位置P 确定方案,使铺设水管费用最低,并求出铺设水管的总费用(精确到0.01万元).APQMNABCD EF A BC DA B CDP2、 逆定理:(1) 如果三角形一条边的平方等于其他两边的平方和,那么这个三角形是直角三角形;利用逆定理来判断三角形是否为直角三角形.(2) 在直角三角形的三边中,首先弄清楚哪条边是斜边,另外应用逆定理时,最大边的平方和等于较小两边的平方和.【例12】 下列命题中是假命题的是()A . 在△ABC 中,若∠B =∠C -∠A ,则△ABC 是直角三角形 B . 在△ABC 中,若2()()a b c b c =+-,则△ABC 是直角三角形 C . 在△ABC 中,若∠B :∠C :∠A =3:4:5,则△ABC 是直角三角形D . △ABC 中,若::5:4:3a b c =,则△ABC 是直角三角形【例13】 (1)将直角三角形的三边都扩大相同的倍数后,得到的三角形是______三角形;(2)若△ABC 的三边A 、B 、C 满足222()()0a b a b c -+-=则△ABC 是________三角形.【例14】 (1)一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,则旗杆折断之前有多少米?(2)如果梯子的底端离建筑物8米,那么17米长的梯子可以到达建筑物的高度是__________米.模块二:勾股定理的逆定理的证明及应用例题解析知识精讲【例15】 ABC ∆的三边分别为A 、B 、C ,且满足222506810a b c a b c +++=++,判断△ABC 的形状.【例16】 如图,公路上A 、B 两点相距25千米,C 、D 为两村庄,DA ⊥AB 于点A ,CB ⊥AB 于点B ,已知DA =15千米,CB =10千米,现要在公路AB 上建一车站E .(1) 若使得C 、D 两村到E 站的距离相等,E 站建在离A 站多少千米处? (2) 若使得C 、D 两村到E 站的距离和最小,E 站建在离A 站多少千米处?【例17】 如图,在四边形ABCD 中,AB =BC =2,CD =3,DA =1,且∠B =90°,求∠DAB 的度数.ABCD A BCDE【例18】 如图,已知在△ABC 中,∠B =90°,AB =BC ,AD 是BC 边上的中线,EF 是AD 的垂直平分线,交AB 于点E ,交AC 于点F ,求AE :BE 的值.3、 距离公式:如果平面内有两点11()A x y ,、22()B x y ,,则A 、B 两点间的距离为:221212()()x x y y -+-.(1) 当11()A x y ,、22()B x y ,两点同在x 轴上或平行于x 轴的直线上,则有12y y =,AB =12||x x -; (2) 当11()A x y ,、22()B x y ,两点同在y 轴上或平行于y 轴的直线上,则有12x x =,AB =12||y y -.【例19】 已知点A (2,2)、B (5,1).(1) 求A 、B 两点间的距离; (2) 在x 轴上找一点C ,使AC =BC .例题解析模块三:两点间的距离公式ABCDEF知识精讲【例20】(1)已知A(x,3)、B(3,x+1)之间的距离为5,则x的值是_________;(2)已知点P在第二、四象限的平分线上,且到Q(2,-3)的距离为5,则点P的坐标为_________.【例21】(1)以点A(1,2)、B(-2,-1),C(4,-1)为顶点的三角形是________;(2)已知点A(0,3)、B(0,-1),△ABC是等边三角形,则点C的坐标是_______.【例22】已知直角坐标平面内的点A(4,1)、B(6,3),在坐标轴上求点P,使P A=PB.【例23】已知直角坐标平面内的点P(4,m),且点P到点A(-2,3)、B(-1,-2)的距离相等,求点P的坐标.【例24】已知点A(2,3)B(4,5),在x轴上是否存在点P,使得PA PB的值最小?若存在,求出这个最小值;若不存在,说明理由.【例25】已知直角坐标平面内的点A(4,32)、B(6,3),在x轴上求一点C,使得△ABC是等腰三角形.【例26】已知点A(4,0)、B(2,-1),点C的坐标是(x,2-x),若△ABC是等腰三角形,求C的坐标.【习题1】六根细木棒,她们的长度分别是2、4、6、8、10、12(单位:cm)从中取出三根,首尾顺次连接搭成一个直角三角形,则这些木棒的长度分别为().A.2、4、8B.4、8、10C.6、8、10D.8、10、12随堂检测【习题2】 已知点A (2,4)B (-1,-3)C (-3,-2),那么△ABC 的形状是()A .等腰三角形B .直角三角形C .等腰直角三角形D .以上都不是【习题3】 (1)如果等腰直角三角形一边长为2,另外两边长为_________;(2)如果直角三角形两边长为5和12,第三边长度为_______________.【习题4】 如图,将长方形ABCD 沿AE 折叠,使得点D 落在BC 上的点F 处,AB =8,AD =10.求EC 的长.【习题5】 如图,在四边形ABCD 中,AB ⊥BC ,AB =9,BC =12,CD =15,DA =152.求四边形ABCD 的面积. A B CDABC DEF【习题6】 如图,在△ABC 中,AD 为BC 边上的中线,AB =5,AC =3,AD =2.求:△ABC 的面积.【习题7】 若A 、B 、C 是三角形的边长且关于x 的方程222()20x a b x c ab -+++=有两个相等的实数根,试判断这个三角形的形状.【习题8】 如图,在一条公路上有P 、Q 两个车站,相距27km ,A 、B 是两个村庄,AP ⊥PQ ,BQ ⊥PQ ,且AP =15km ,BQ =24km ,现在要在公路上建立一个商场M 使得A 、B 两个村庄到商场M 的距离相等,求PM 的长 .【习题9】 已知点()()2814A B -,,,点C 在y 轴上,使ABC ∆为直角直角三角形,求满足条件的点C 的坐标.AB D CABQP M【习题10】 如图,在ABC ∆中,90ACB AC BC M ∠==o ,,是ABC ∆内一点,且 312AM BM CM ===,,,求BMC ∠的度数.【习题11】 若在△ABC 中,AB =c ,AC =b ,BC =a ,∠ACB =90°,则222a b c +=试用两种方法证明.【作业1】 下列命题中,正确的有()个(1) 腰长及底边上的高对应相等的两个等腰三角形全等 (2) 有一直角边和斜边上对应相等的两个直角三角形全等 (3) 有两边和其中一边上的高对应相等的两个三角形全等 A .0 B .1 C .2 D .3课后作业ABCM【作业2】 如图,图中的字母、数代表正方形的面积,则A =______.【作业3】 如图,Rt ABC ∆中,斜边1AB =,则222AB BC AC ++的值是_________.【作业4】 已知点()35A -,,点B 的横坐标为-3,且A 、B 两点之间的距离为10,那么点B 的坐标是____________.【作业5】 现将直角三角形ABC 的直角边AC 沿直线AD 折叠,使它落在斜边AB 上,C 与E 重合,且AC =3,BC =4,则CD 等于_____________.【作业6】 如果ABC ∆的周长为12,而22AB BC AC AB BC +=-=,,那么ABC ∆的形状是 ____________.【作业7】 已知等腰直角三角形ABC 斜边BC 的长为2,DBC ∆为等边三角形,那么A 、D 两点的距离为_______. 5072A【作业8】 知:如图,已知在Rt ABC ∆中,9030B C ∠=∠=o o ,,将ABC ∆绕点A 逆时针旋转30o 后得到APQ ∆,若1AB =,则两个三角形重叠部分的面积为_________.【作业9】 已知:如图,四边形ABCD 的三边(AB 、BC 、CD )和BD 都为5厘米,动点P 从A 出发(A B D →→),速度为2厘米/秒,动点Q 从点D 出发(D C B A →→→)到A ,速度为2.8厘米/秒,5秒后P 、Q 相距3厘米,试确定5秒时APQ ∆的形状.【作业10】 阅读下列题目的解题过程: 已知a 、b 、c 为ABC ∆的三边,且满足222244a c b c a b -=-,试判断ABC ∆的形状.解:Q 222244a c b c a b -=-(A ),()()()2222222c a b a b a b ∴-=+-(B )222c a b ∴=+(C ),∴ABC ∆是直角三角形.问:(1)上述解题过程中,从哪一步开始出错? 请写出该步的代号:____________; (2)错误的原因:_______________;(3)本题正确的结论为:____________.ABCDQPABCQP【作业11】 如图,一根长度为50CM 的木棒的两端系着一根长度为70CM 的绳子,现准备在绳子上找一点,然后将绳子拉直,使拉直后的绳子与木棒构成一个直角三角形,求满足条件的点有几个,并且这个点将绳子分成的两段各有多长?【作业12】 在直角坐标平面内,已知()()1054A B -,,,,在坐标轴上求一点P ,使得PAB ∆为直角三角形,求点P 的坐标.。

高中几何知识解析勾股定理的证明与应用一、勾股定理的证明勾股定理是数学中最基础的几何定理之一,也是高中数学必学的重要内容。
下面我们将介绍几种常见的证明方法。
1. 几何法证明:勾股定理最常见的证明方法之一是几何法证明。
具体的证明过程可以用一个平面直角三角形来说明。
假设在直角三角形ABC中,角C为直角,边AC与边BC分别记为a和b,边AB记为c。
我们可以通过将边BC沿AC边作为底边展开,构造一个以直角三角形ABC为底面的正方形ABDE以及一个以边AC为直径的半圆。
首先,我们可以发现正方形ABDE的边长等于c,而半圆的直径为AB,即也等于c。
由于正方形的面积等于边长的平方,所以正方形ABDE的面积为c²,而半圆的面积为πc²/4(其中π为圆周率)。
接下来,我们可以将正方形ABDE切割成4个直角三角形,它们与直角三角形ABC面积相等。
将这些三角形沿AC边折叠,可以将它们放置在以边AC和边BC为直径的半圆内。
由于直角三角形ABC的面积等于这些折叠后的三角形的面积之和,即等于半圆的面积减去正方形的面积。
代入式子,我们可以得到:a*b/2 = πc²/4 - c²,化简后可以得到勾股定理的成立:a² + b² = c²。
2. 代数法证明:除了几何法证明外,我们还可以通过代数法来证明勾股定理。
我们可以用平面直角坐标系表示直角三角形ABC,假设顶点A位于原点,点B的坐标为(c, 0),点C的坐标为(0, b)。
根据直角三角形的定义,我们可以得到点C与点B的连线为直角边AC,点A与点C的连线为直角边BC。
根据坐标公式,直角边AC和BC的长度分别为a和b。
根据两点间距离公式,我们可以得到:a = √((0 - c)² + (b - 0)²) = √(c² + b²),二次方根表示距离的长度,代入式子,我们可以得到勾股定理的成立:a² + b² = c²。

两点间的距离公式是什么斜率引言在数学和物理学中,距离是两点之间的量度。
计算两点之间的距离是一种常见的问题,而几何学中有一个公式可以用来计算两点之间的距离。
此外,在数学中,斜率用于描述直线的倾斜程度。
本文将介绍两点之间的距离公式和斜率的概念,并给出相应的计算方法。
两点之间的距离公式设平面上有两点A(x1, y1)和B(x2, y2),我们想要计算这两点之间的距离。
根据勾股定理,在直角三角形中,距离可以通过两点之间的水平和垂直位移来计算。
根据这一原理,我们可以得出两点之间的距离公式。
步骤1.计算水平位移:水平位移可以通过点A和点B的x坐标之差来计算:dx = x2 - x1。
2.计算垂直位移:垂直位移可以通过点A和点B的y坐标之差来计算:dy = y2 - y1。
3.应用勾股定理:利用勾股定理,我们可以计算两点之间的距离d。
根据勾股定理,直角三角形的斜边长度等于两条直角边长度的平方和的平方根。
因此,距离可以计算如下:d = √(dx² + dy²)。
示例假设有两个点A(1, 2)和B(4, 6)。
我们可以按照上述步骤计算它们之间的距离:1.计算水平位移:dx = 4 - 1 = 3。
2.计算垂直位移:dy = 6 - 2 = 4。
3.应用勾股定理:d = √(3² + 4²) ≈ √(9 + 16) ≈ √25 = 5。
因此,点A和点B之间的距离为5个单位。
斜率的概念斜率是用于描述直线的倾斜程度的度量。
直线的斜率是指线段在水平方向上的位移与垂直方向上的位移之比。
计算斜率给定直线上的两个点A(x1, y1)和B(x2, y2),我们可以通过以下公式来计算斜率:斜率(m)= (y2 − y1) / (x2 − x1)示例假设有两个点A(2, 3)和B(6, 9)。
我们可以按照上述公式计算它们之间的斜率:斜率(m)= (9 − 3) / (6 − 2) = 6 / 4 = 1.5因此,直线AB的斜率为1.5。
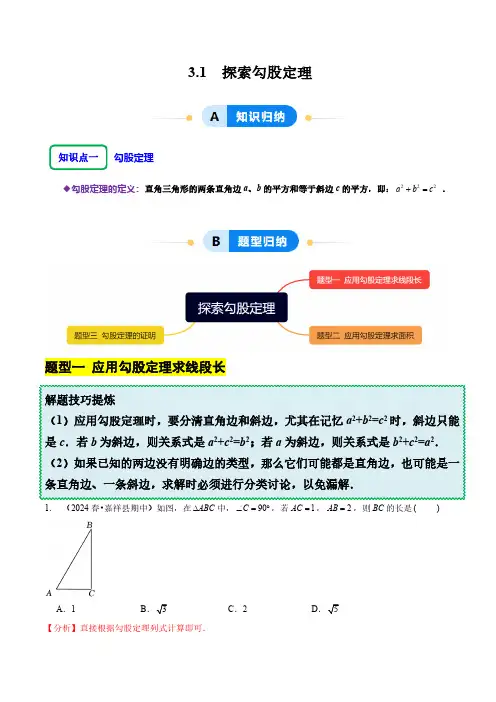
3.1 探索勾股定理◆勾股定理的定义:直角三角形的两条直角边a 、b 的平方和等于斜边c 的平方,即:222a b c += .题型一 应用勾股定理求线段长1.(2024春•嘉祥县期中)如图,在ABC D中,90C Ð=°,若1AC =,2AB =,则BC 的长是( )A .1BC .2D 【分析】直接根据勾股定理列式计算即可.【解答】解:90C Ð=°Q ,1AC =,2AB =,BC \===即BC 故选:B .2.(2023秋•临淄区期末)如图,在Rt ABC D 中,90ACB Ð=°,3BC =,4AC =,CD AB ^于点D ,E是AB 的中点,则DE 的长为( )A .0.6B .0.7C .0.8D .0.9【分析】由勾股定理求出AB 长,由三角形面积公式求出CD 长,由勾股定理求出BD 长,由线段中点定义求出BE 长,即可得到0.7DE BE BD =-=.【解答】解:90ACB Ð=°Q ,3BC =,4AC =,5AB \==,CD AB ^Q 于点D ,ABC \D 的面积1122BC CA AB CD =×=×,345CD \´=,2.4CD \=,1.8BD \==,E Q 是AB 的中点,1 2.52BE AB \==,0.7DE BE BD \=-=.故选:B .题型二 应用勾股定理求面积1.(2024春•齐河县校级月考)如图,字母B 所代表的正方形的面积是( )A .12 2cmB .15 2cmC .144 2cmD .306 2cm 【分析】如图,利用勾股定理得到222a b c +=,再根据正方形的面积公式得到281a =,2225c =,则可计算出2144b =,从而得到字母B 所代表的正方形的面积.【解答】解:如图,222a b c +=Q ,而281a =,2225c =,222581144b \=-=,\字母B 所代表的正方形的面积为2144cm .故选:C .2.(2022秋•郓城县期中)如图,在Rt ABC D 中,90C Ð=°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,当4AC =,2BC =时,则阴影部分的面积为( )A .4B .4pC .8pD .8【分析】根据勾股定理得到222AB AC BC =+,根据扇形面积公式计算即可.【解答】解:由勾股定理得,22220AB AC BC =+=,则阴影部分的面积2221111()((2222222AC BC AB AC BC p p p =´´+´´+´´-´´22211124()224AC BC AB p =´´+´´´+-4=,故选:A .3.(2024春•济南期末)已知,如图长方形ABCD 中,3AB cm =,9AD cm =,将此长方形折叠,使点B与点D 重合,折痕为EF ,则ABE D 的面积为( )A .23cmB .24cmC .26cmD .212cm 【分析】根据折叠的条件可得:BE DE =,在直角ABE D 中,利用勾股定理就可以求解.【解答】解:将此长方形折叠,使点B 与点D 重合,BE ED \=.9AD cm AE DE AE BE ==+=+Q .9BE AE \=-,根据勾股定理可知222AB AE BE +=.解得4AE =.ABE \D 的面积为23426()cm ´¸=.故选:C .4.(2023秋•阳信县期末)如图,在Rt ABC D 中,90C Ð=°,若15AB =,则正方形ADEC 和正方形BCFG 的面积和为( )A .225B .200C .150D .无法计算【分析】根据勾股定理得222215225AC BC AB +===,从而得出答案.【解答】解:在Rt ABC D 中,90C Ð=°,由勾股定理得,222215225AC BC AB +===,\正方形ADEC 和正方形BCFG 的面积和为225,故选:A .5.(2024春•沂水县校级月考)如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )A .50B .16C .25D .41【分析】根据勾股定理求出2AB ,再根据勾股定理计算即可.【解答】解:由勾股定理得,222131225AB =-=,22225CD BD BC \+==,\阴影部分的面积252550=+=,故选:A .6.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是( )A.16B.25C.144D.169【分析】根据勾股定理解答即可.【解答】解:AB===,根据勾股定理得出:5\==,EF AB5\阴影部分面积是25,故选:B.题型三勾股定理的证明1.(2024春•历下区期末)勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端,下面四幅图中不能证明勾股定理的是( )A .B .C .D .【分析】先用不同方法表示出图形中各个部分的面积,利用面积不变得到等式,变形再判断即可.【解答】解:A .大正方形的面积等于四个矩形的面积的和,222()2a b a ab b \+=++,以上公式为完全平方公式,A \选项不能说明勾股定理;B .由图可知三个三角形的面积的和等于梯形的面积,\21111()()2222ab ab c a b a b ++=++,整理得222a b c +=,B \选项可以证明勾股定理;C .大正方形的面积等于四个三角形的面积加小正方形的面积,2214()2ab c a b \´+=+,整理得222a b c +=,C \选项可以证明勾股定理;D .整个图形的面积等于边长为b 的正方形的面积+边长为a 的正方形面积2+个直角三角形的面积,也等于边长为c 的正方形面积2+个直角三角形的面积,222112222b a abc ab \++´=+´,整理得222a b c +=,D \选项可以证明勾股定理,故选:A .2.(2024春•梁山县校级月考)如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.如果直角三角形较长直角边的长为a ,较短直角边的长为b ,若7ab =,大正方形的面积为30,则小正方形的边长为( )A .16B .8C .4D .2【分析】由题意可知:中间小正方形的边长为:a b -,根据勾股定理以及题目给出的已知数据即可求出小正方形的边长.【解答】解:由题意可知:中间小正方形的边长为:a b -,Q 每一个直角三角形的面积为:1177222ab =´=,\214()302ab a b ´+-=,2()301416a b \-=-=,4a b \-=,故选:C .3.(2024春•阳谷县校级月考)如图是“赵爽弦图”,它是由4个全等的直角三角形拼成的图形,若大正方形的面积是29,小正方形的面积是9,设直角三角形较长直角边为b ,较短直角边为a ,则a b +的值是( )A .5B .6C .7D .8【分析】根据勾股定理求出22a b +等于大正方形的面积,求出四个直角三角形的面积,得出ab 的值,求解.【解答】解:Q 大正方形的面积是29,小正方形的面积是9.\一个小三角形的面积是1(299)54´-=\152ab =.2229a b +=.222()249a b a b ab \+=++=.7a b \+=.故选:C .4.(2024春•嘉祥县期中)如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形的面积是17,小正方形的面积是5,直角三角形较长直角边为a ,较短直角边为b ,则2()a b +的值是( )A .25B .17C .29D .22【分析】根据正方形的面积及直角边的关系,列出方程组,然后求解.【解答】解:由条件可得22171175240a b ab a b ì+=ï-ï=íï>>ïî,即2217a b +=,212ab =,则222()2171229a b a b ab +=++=+=,所以2()29a b +=,故选:C .5.(2023秋•邹平市期末)下面图形能够验证勾股定理的有( )A .0B .1C .2D .3【分析】利用面积法证明勾股定理即可解决问题.【解答】解:第一个图形:中间小正方形的面积221()42c a b ab =+-´;化简得222c a b =+,可以证明勾股定理.第二个图形:中间小正方形的面积221()42b ac ab -=-´;化简得222a b c +=,可以证明勾股定理.第三个图形:梯形的面积2111()()2222a b a b ab c =++=´´+,化简得222a b c +=;可以证明勾股定理.故能够验证勾股定理的有3个.故选:D .6.(2022春•兖州区期末)我国是最早了解勾股定理的国家之一.据《周髀算经》记载,勾股定理的公式与证明是在商代由商高发现的,故又称之为“商高定理”;三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释,并给出了另外一个证明,下面四幅图中,不能证明勾股定理的是( )A .B .C .D .【分析】根据基础图形的面积公式表示出各个选项的面积,同时根据割补的思想可以写出另外一种面积表示方法,即可得出一个等式,进而可判断能否证明勾股定理.【解答】解:A 、大正方形的面积为:2c ;也可看作是4个直角三角形和一个小正方形组成,则其面积为:22214()2ab b a a b ´+-=+,222a b c \+=,故A 选项能证明勾股定理.B 、梯形的面积为:2211()()()22a b a b a b ab ×++=++;也可看作是2个直角三角形和一个等腰直角三角形组成,则其面积为:221112222ab c ab c ´+=+,\22211()22ab c a b ab +=++,222a b c \+=,故B 选项能证明勾股定理.C 、大正方形的面积为:2()a b +;也可看作是4个直角三角形和一个小正方形组成,则其面积为:221422ab c ab c ´+=+,22()2a b ab c \+=+,222a b c \+=,故C 选项能证明勾股定理.D 、大正方形的面积为:2()a b +;也可看作是2个矩形和2个小正方形组成,则其面积为:222a b ab ++,222()2a b a b ab \+=++,D \选项不能证明勾股定理.故选:D .7.(2024春•齐河县校级月考)如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,如果大正方形的面积为16,小正方形的面积为3,那么2()a b +的值为 .【分析】根据所求问题,利用勾股定理得到22a b +的值,由已知条件得到ab 的值,根据完全平方公式即可求解.【解答】解:Q 大正方形的面积为16,2216a b \+=,由题意143162ab ´+=,213ab =,222()2161329a b a ab b \+=++=+=,故答案为:29.8.(2015秋•滕州市校级期末)如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,若直角三角形的两边长分别为3和5,则小正方形的面积为 .【分析】分两种情况:①5为斜边时,由勾股定理求出另一直角边长为4,小正方形的边长431=-=,即可得出小正方形的面积;②3和5为两条直角边长时,求出小正方形的边长2=,即可得出小正方形的面积;即可得出结果.【解答】解:分两种情况:①5为斜边时,由勾股定理得:另一直角边长4==,\小正方形的边长431=-=,\小正方形的面积211==;②3和5为两条直角边长时,小正方形的边长532=-=,\小正方形的面积224=;综上所述:小正方形的面积为1或4;故答案为:1或4.9.(2024春•河东区校级月考)阅读下列材料,并完成相应任务.教材第九章探索整式乘法法则时,我们用不同方法表示同一个图形的面积,直观地理解乘法法则.如图1,现有4张大小形状相同的直角三角形纸片,三边长分别是a 、b 、c ,将它们拼成如图2的大正方形.(1)观察:图2中,大正方形的面积可以用2()a b +表示,也可以用含a 、b 、c 的代数式表示为 2142ab c ´+ ,那么可以得到等式: .整理后,得到a 、b 、c 之间的数量关系:222a b c +=,这就是著名的“勾股定理”,它反映了直角三角形的三边关系,即直角三角形的两直角边a 、b 与斜边c 所满足的关系式.(2)思考:爱动脑的小明通过图2得到启示,发现其它图形也能验证“勾股定理”,请你帮助小明画出该图形.(画出一种即可)(3)应用:如图3,在直角三角形ABC 中,90C Ð=°,3AC =,4BC =,那么AB = ,点D 为射线BC 上一点,将ACD D 沿AD 所在直线翻折,点C 的对应点为点1C ,如果点1C 在射线BA 上,那么CD = .(直接写出答案)【分析】(1)将正方形的面积表示成4个直角三角形的面积加中间小正方形的面积,即可用含a 、b 、c 的代数式表示出大正方形的面积;根据同一个图形用不同方法表示出其面积,面积不变即可得到等式;(2)此题的方法很多,这里只举一种例子即可,比如把两个直角三角形和一个等腰直角三角形组成一个梯形;(3)分两种情况:点D 在BC 上和点D 在BC 延长线上,并分别画出图形,在Rt BDC ¢D 中利用勾股定理列方程解出即可.【解答】解:(1)由图形可知:正方形的面积也可表示成4个直角三角形的面积加中间小正方形的面积,即2142ab c ´+,Q 用不同的方法表示同一个图形的面积,面积不变,221()42a b ab c \+=´+,故答案为:2142ab c ´+,221()42a b ab c +=´+;(2)答案不唯一,比如:(3)在直角三角形ABC 中,90C Ð=°,3AC =,4BC =,由勾股定理,得5AB ===,点D 为射线BC 上一点,分两种情况:①点D 在BC 上时,如图,设CD x =,由翻折可知C D x ¢=,4BD BC CD x =-=-,532BC AB AC AB AC ¢¢=-=-=-=,在Rt BDC ¢D 中,由勾股定理,得222BD BC DC ¢¢=+,即222(4)2x x -=+,解得32x =;②点D 在BC 的延长线上时,如图,设CD y =,由翻折可知C D y ¢=,4BD BC CD y =+=+,538BC AB AC AB AC ¢¢=+=+=+=,在Rt BDC ¢D 中,由勾股定理,得222BD BC DC ¢¢=+,即222(4)8y y +=+,解得6y =.故答案为:32或6.10.(2024春•兰山区校级月考)如图①,直角三角形的两条直角边长分别是a ,()b a b <,斜边长为c .(1)探究:用四个这样的直角三角形拼成一大一小两个正方形(如图②).①小正方形的边长为c ,大正方形的边长为 ;②由大正方形面积的不同表示方式可以得出等式 ,整理得 ,从而验证勾股定理;(2)应用:将两个这样的直角三角形按图③所示摆放,使BC 和CD 在一条直线上,连接AE .请你类比(1)中的方法用图③验证勾股定理.【分析】(1)用两种方法表示出大正方形的面积,即可;(2)利用等积法进行证明即可.【解答】解:(1)①由图和题意可知:大正方形的边长为a b +;故答案为:a b +;②由大正方形面积的不同表示方式可以得出等式221()42a b ab c +=´+,整理得222a b c +=;故答案为:221()42a b ab c +=´+,222a b c +=;(2)90BAC ACB Ð+Ð=°Q ,BAC ECD Ð=Ð,90ECD ACB \Ð+Ð=°,90ACE \Ð=°用两种不同的方法表示出梯形ABDE 的面积,可得:2111()()2222a b a b ab c ++=´+,22222a ab b ab c \++=+,222a b c \+=.11.(2024春•昌乐县期中)公元3世纪,古人就通过拼图验证了勾股定理:在直角三角形中两直角边a 、b 与斜边c 满足关系式222a b c +=.还探索验证了勾股定理的逆定理:如果三角形三边满足222a b c +=,则这个三角形是直角三角形.(1)小明发现证明勾股定理的新方法:如图1,在正方形ACDE 边CD 上取点B ,连接AB ,得到Rt ACB D ,三边分别为a ,b ,c ,剪下ACB D 把它拼接到AEF D 的位置,如图2所示,请利用面积不变证明勾股定理.(2)一个零件的形状如图3,按规定这个零件中A Ð和C Ð都应是直角,小明测得这个零件各边尺寸(单位:)cm 如图③所示,这个零件符合要求吗?【分析】(1)连接BF ,由图1可得正方形ACDE 的面积为2b ,由图2可得四边形ABDF 的面积为三角形ABF 与三角形BDF 面积之和,再利用正方形ACDE 的面积与四边形ABDF 的面积相等即可证明;(2)利用反证法,根据勾股定理的逆定理验证A Ð,C Ð是否为直角即可判断这个零件是否符合要求.【解答】(1)证明:如图,连接BF ,AC b =Q ,\正方形ACDE 的面积为2b ,CD DE AC b ===Q ,BC a =,EF BC a ==,BD CD BC b a \=-=-,DF DE EF a b =+=+,90CAE Ð=°Q ,90BAC BAE \Ð+Ð=°,BAC EAE Ð=ÐQ ,90EAF BAE \Ð+Ð=°,BAF \D 为等腰直角三角形,\四边形ABDF 的面积为:2222()()()c b a a b c b a +-+=+-,Q 正方形ACDE 的面积与四边形ABDF 的面积相等,2222()b c b a \=+-,2222b c b a \=+-,222a b c \+=,222a b c \+=.(2)解:这个零件不符合要求.理由如下:连接BD ,如图,由勾股定理逆定理,知只有当22222BC DC AB AD BD +=+=时,A Ð和C Ð都是直角,22221520225400625BC DC +=+=+=Q ,222223852964593AB AD +=+=+=,且625593¹,2222BC DC AB AD \+¹+,所以A Ð和C Ð不可能都是直角.因此,这个零件不符合要求.12.(2024春•长清区期中)(1)计算:(2)()a b a b ++= ;(2)图形是一种重要的数学语言,它直观形象,我们可以用几何图形的面积来解释一些代数中的等量关系.例如:上面的计算是否正确我们可以通过图1来进行验证和解释.请同学们分别写出图2、图3能解释的乘法公式:图2: ;图3: ;(3)利用几何图形的面积,我们还可以去探究一些其它的等量关系:做4个全等的直角三角形,设它们的两条直角边分别为a ,b ,斜边为c ,再做1个长分别为c 的正方形,把它们按图4所示的方式拼成一个大正方形.试用不同的方法计算正方形的面积,就可以得到直角三角形的三边的数量关系:222a b c +=.这一个数量关系,我们叫做“勾股定理”,请你利用图4来证明勾股定理,即222a b c +=.(4)如图5,在Rt ABC D 中,90ACB Ð=°,CD 是AB 边上高,4AC =,3BC =,求CD 的长度.【分析】(1)利用多项式乘多项式的运算法则进行计算即可;(2)根据图形的两种面积计算方法即可得出的答案;(3)在图4中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和得出221()42a b c ab +=+´,然后化简即可求证;(4)先求出5AB =,再根据等面积法即可求得.【解答】解:(1)原式22222223a ab ab b a ab b =+++=++.故答案为:2223a ab b ++.(2)222()2a b a ab b -=-+,(a b + 22)()a b a b -=-,故答案为:222()2a b a ab b -=-+;(a b + 22)()a b a b -=-.(3)在图4中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,即221()42a b c ab +=+´,化简,得222a b c +=.(4)在Rt ABC D 中,90ACB Ð=°Q ,\由勾股定理得222224325AB AC BC =+=+=5AB \=,CD AB^Q,\1122ABCS AC BC AB CDD=×=×,\431255 CD´==.。
本章节主要讲解两部分内容,一是直角三角形的三条边之间的数量关系即勾股定理,包括勾股定理的证明、应用及逆定理的证明和应用两方面;二是两点间的距离公式.难点是勾股定理的证明及应用,它是解决直角三角形三边之间关系的常用方法,是一个工具公式,在以后的学习中运用非常广泛.1、勾股定理:(1)直角三角形中,两条直角边的平方和,等于斜边的平方.利用勾股定理往往构造方程,已达到解决问题的目的;(2)应用勾股定理解决实际问题,要注意分析题目的条件,关注其中是否存在直角三角形,如果存在直角三角形,根据所给的三边条件,建立方程,从而解决问题;如果问题中没有直角三角形,可以通过添加辅助线构造出直角三角形,寻求等量关系,再根据勾股定理建立相应的方程,因此,在解决直角三角形中有关边长的问题时,要灵活的运用方程的思想.勾股定理及两点间的距离公式知识结构模块一:勾股定理的证明及应用例题解析知识精讲内容分析【例1】 (1)在直角△ABC 中,∠C =90°,∠A =30°,BC =1,则AB =_________; (2)在直角△ABC 中,∠C =90°,∠A =45°,AB =3,则AC =_________.【答案】(1)2;(2)223.【解析】(1)由直角三角形性质推论即可得结论;(2)设x BC AC ==,则由勾股定理可得:2223=+x x ,解得:223=x , ∴223=AC . 【总结】考察直角三角形的性质和勾股定理的综合应用.【例2】 (1)等边三角形的边长是3,则此三角形的面积是___________;(2)等腰三角形底边上的长为2,腰长为4,则它底边上的高为__________.【答案】(1)349;(2)15.【解析】(1)作出等边三角形的高,则可得高为323,则三角形的面积为349; (2)作底边上的高,由三线合一性质和勾股定理可得底边上的高为15 【总结】考察等腰三角形的三线合一和勾股定理的综合运用.【例3】 (1)直角三角形两边长为3和4,则此三角形第三边长为_________;(2)直角三角形两直角边长为3和4,则此三角形斜边上的高为_________; (3)等腰三角形两边长是2、4,则它腰上的高是____________.【答案】(1)5或7;(2)512;(3)215.【解析】(1)3和4可以是两直角边长,也可以是一个直角边和斜边; (2)由勾股定理可得:斜边长为5,则由等面积法可知:三角形斜边上的高为512543=⨯;(3)∵2、2、4不能构成三角形,所以三角形的三边长为4、4、2, 作等腰三角底边上的高,则由等腰三角形三线合一性质和勾股定理可得:底边上的高为15,则由等面积法可知:此三角形腰上的高为2154152=⨯. 【总结】考察等腰三角形的性质和勾股定理的应用,注意分类讨论.【例4】 (1)若直角三角形的三边长分别为N +1,N +2,N +3则N 的值是____________;(2)如果直角三角形的三边长为连续偶数,则此三角形的周长为______________.【答案】(1)2;(2)24.【解析】(1)由题意有:()()()222321+=+++N N N ,解:2=N (负值舍去);(2)可设直角三角形的三边长分别为N -2,N ,N +2 ∴()()22222+=+-N N N ,∴8=N∴三角形的周长为243=N【总结】考察勾股定理的应用.【例5】 如图,在直角△ABC 中,∠ACB =90°,∠B=60°,D 是斜边AB 的中点,BC =2,求△ADC 的周长. 【答案】324+.【解析】∵∠ACB =90°,D 是斜边AB 的中点,∴AB AD CD BD 21===.∵∠B=60°,∴△BDC 是等边三角形,∴BC CD =.∵∠ACB =90°,∠B=60°,∴∠A=30°,∴4=AB .∵AB AD CD BD 21===,∴2=CD .∵∠ACB =90°,BC =2,4=AB ,∴322422=-=AC ,∴3243222+=++=++=AC CD AD C ADC △ 【总结】考察直角三角形的性质和勾股定理的运用.【例6】 如图,已知:R t △ABC 中,∠ACB 是直角,BC =15,AB 比AC 大9,CD ⊥AB 于点D ,求CD 的长.【答案】17120.【解析】设9AC x AB x ==+,, ∵222CB AC AB +=,∴()222159+=+x x ,解得:8=x∴817AC AB ==,由等面积法可知:1712017158=÷⨯=÷⋅=AB BC AC CD . 【总结】考察勾股定理和等面积法的应用.【例7】 已知已直角三角形的周长为4+26,斜边上的中线为2,求这个直角三角形的面积.【答案】52.【解析】∵斜边上的中线为2,所以斜边长为4.A BCDBC D∵直角三角形的周长为4+26,∴两直角边之和为26. ∵斜边长为4,则两直角边的平方和为16,∴设两直角边分别为x y ,,则有⎩⎨⎧=+=+261622y x y x ,解得:()()52222=+-+=y x y x xy ,∴直角三角形的面积为25. 【总结】考察勾股定理和直角三角形性质的应用,解题时注意方法的运用.【例8】 如图,直线MN 是沿南北方向的一条公路,某施工队在公路的点A 测得北偏西30°的方向上有一栋别墅C ,朝正北方向走了400米到达点B 后,测得别墅C 在北偏西75°的方向上,如果要从别墅C 修一条通向MN 的最短小路, 请你求出这条小路的长(结果保留根号). 【答案】3100100+.【解析】根据垂线段最短,过C 作垂线的垂线段是最短的. 过C 作CD ⊥MN ,垂足为D ,过B 作BE ⊥AC ,垂足为E . 由题意可知:︒=∠30CAB ,︒=∠75CBM ,∴︒=∠45BCA .在Rt △ABE 中,︒=∠30CAB ,400=AB ,∴20021==AB BE .∴由勾股定理可得:3200=AE在Rt △CBE 中,︒=∠45BCA ,200=BE ,∴200=CE ∴2002200+=+=CE AE AC在Rt △ACD 中,︒=∠30CAB ,3200200+=AC ,∴3100100+=CD .【总结】考察勾股定理和直角三角形性质的应用.【例9】 如图,公路MN 和公里PQ 在点P 处交汇,且∠QPN =30°,点A 处有一所中学,AP =160米,假设拖拉机行驶时,周围100米以内会受到噪音的影响,那么拖拉机在MN 上沿PN 方向行驶时,学校是否会受到噪音的影响?请说明理由;如果受影响,已知拖拉机的速度是18千米/时,那么学校受影响的时间是多少秒? 【答案】24秒.【解析】过A 做AB ⊥MN ,垂足为B .A BCM M ND ME M APQ MNB在Rt △ABP 中,∠QPN =30°,160=AP ,∴8021==AP AB∵80<100,所以学校会受到噪音的影响.假设在C 处开始受到噪音影响,在D 处开始不受影响, ∴100100==AD CA ,由勾股定理可得:60==BD CB∴受影响的路程为120米=0.12千米∴学校受影响的时间为秒2436001812.0=⨯.【总结】考察勾股定理和直角三角形性质的应用,解题时注意对题意的分析.【例10】 如图,矩形ABCD 中,AB =8,BC =4,将矩形沿AC 进行翻折,点D 落在E 处,求出重叠部分△AFC 的面积. 【答案】10.【解析】∵AB DC ∥,ACF DCA ∠=∠,∴CAF ACF ∠=∠,∴FC AF = 设x FC AF ==,则x FB -=8∵222CF BF BC =+,∴()22284x x =-+,解得:5=x∴10452121=⨯⨯=⋅⋅=CB AF S AFC △ 【总结】考察翻折图形的性质和勾股定理的应用.【例11】 如图,AB 两个村子在河边CD 的同侧,A 、B 两村到河边的距离分别为AC =1千米,BD =3千米,CD =3千米.现在河边CD 建一座水厂,建成后的水厂,可以直接向A 、B 两村送水,也可以将水送一村再转送另一村.铺设水管费用为每千米2万元,试在河边CD 选择水厂位置P 确定方案,使铺设水管费用最低,并求出铺设水管的总费用(精确到0.01万元). 【答案】10万元.【解析】延长AC 至点E ,使得CE =AC ,连接EB 交CD 于一点,,则此时铺设水管费用最低. 过E 作EF ∥CD ,交BD 延长线于F ∵四边形CEFD 是长方形,∴1==DF CEABCDEFABC D AB C D PEF∵34EF BF ==,,∴由勾股定理可得:5=BE 此时5==+=+BE BP EP PB AP ∴总费用为1025=⨯万元.【总结】考察勾股定理在实际问题中的应用.【例12】 如图,在直角△ABC 中,∠BAC =90°,AB =AC ,E 、F 是BC 上的两点,且∠EAF =45°,求证:222+=BE CF EF . 【答案】见解析【解析】过C 作CG ⊥BC ,使CG CE =,连接AG 、FG .∵∠BAC =90°,AB =AC , ∴45B BCA ∠=∠=.∵CG ⊥BC , ∴45ACG BCA ∠=∠=, ∴ACG B ∠=∠. ∵AB =AC ,BE =CG , ∴AEB AGC △≌△∴AE AG BAE CAG =∠=∠,. ∵︒=∠45EAF , ∴︒=∠+∠45CAF BAE ,∴45CAF CAG ∠+∠=︒,即45FAG ∠=︒, ∴GAF EAF ∠=∠∵AF AF =,AE AG =, ∴AFG AFE △≌△, ∴EF GF =.在Rt CFG 中,由勾股定理,可得:222GF CG CF =+, 又EF GF =,CG CE =,∴222+=BE CF EF .【总结】本题综合性较强,本质上是对三角形的旋转,同时结合了勾股定理进行解题.ABC EFG2、 逆定理:(1) 如果三角形一条边的平方等于其他两边的平方和,那么这个三角形是直角三角形;利用逆定理来判断三角形是否为直角三角形.(2) 在直角三角形的三边中,首先弄清楚哪条边是斜边,另外应用逆定理时,最大边的平方和等于较小两边的平方和.【例13】 下列命题中是假命题的是()A . 在△ABC 中,若∠B =∠C -∠A ,则△ABC 是直角三角形 B . 在△ABC 中,若2()()a b c b c =+-,则△ABC 是直角三角形 C . 在△ABC 中,若∠B :∠C :∠A =3:4:5,则△ABC 是直角三角形D . △ABC 中,若::5:4:3a b c =,则△ABC 是直角三角形 【答案】C【解析】A 答案中:C A B ∠=∠+∠,且C A B ∠-︒=∠+∠180,∴︒=∠90C ,所以是直角三角形;B 答案中:222c b a -=,∴222b c a =+,所以是直角三角形;C 答案中:x A x C x B 5,4,3=∠=∠=∠,∴︒=++180543x x x ,∴︒=15x ,∴︒=∠75C , ∴不是直角三角形;D 答案中:设543a m b m c m ===,,,∵222c b a +=,所以是直角三角形. 【总结】考察判断直角三角形的方法.模块二:勾股定理的逆定理的证明及应用例题解析知识精讲【例14】 (1)将直角三角形的三边都扩大相同的倍数后,得到的三角形是______三角形;(2)若△ABC 的三边A 、B 、C 满足222()()0a b a b c -+-=则△ABC 是________三角形. 【答案】(1)直角三角形;(2)等腰三角形或直角三角形.【解析】(1)直角三角形的三边都扩大相同的倍数后,三边也满足勾股定理,所以得到的三角形是直角三角形;(2)由题意有:b a =或222c b a =+,∴三角形为等腰三角形或直角三角形. 【总结】考察勾股定理的应用.【例15】 (1)一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,则旗杆折断之前有多少米?(2)如果梯子的底端离建筑物8米,那么17米长的梯子可以到达建筑物的高度是__________米.【答案】(1)24米;(2)15米.【解析】(1)由题意可知:折断的旗杆的部分长度为1512922=+,则旗杆长为9+15=24米;(2)由题意可得:可达到建筑物的高度为1581722=-. 【总结】考察勾股定理在实际问题中的应用.【例16】 ABC ∆的三边分别为A 、B 、C ,且满足222506810a b c a b c +++=++, 判断△ABC 的形状.【解析】∵222506810a b c a b c +++=++,∴()()()0543222=-+-+-c b a ,∴345a b c ===,,.∵222c b a =+,∴△ABC 是直角三角形.【总结】考察完全平方公式的应用和勾股定理逆定理的运用.【例17】 如图,公路上A 、B 两点相距25千米,C 、D 为两村庄,DA ⊥AB 于点A ,CB ⊥AB 于点B ,已知DA =15千米,CB =10千米,现要在公路AB 上建一车站E . (1) 若使得C 、D 两村到E 站的距离相等,E 站建在离A 站多少千米处? (2) 若使得C 、D 两村到E 站的距离和最小,E 站建在离A 站多少千米处?【答案】(1)10=AE ;(2)15AE =.ABCDE E’【解析】(1)设25AE x BE x ==-,则,∴()222222152510ED x EC x =+=-+,,∵EC ED =,∴()2222102515+-=+x x ,∴10=x ,即10=AE .(2)找出C 点关于AB 的对称点F ,联结DF 交AB 于点E ', 则此时的E '满足C 、D 两村到E 站的距离和最小, 设x BE x AE -==25,,∴()222222152510ED x EF x =+=-+,, ∵225252522=+=DF ,∴()2251025152222=+-++x x ,解得:15x =,∴15AE =【总结】考察勾股定理的应用,注意最小值的求法.【例18】 如图,在四边形ABCD 中,AB =BC =2,CD =3,DA =1,且∠B =90°,求∠DAB的度数. 【答案】135°. 【解析】连接AC∵AB =BC =2,∠B =90°,∴222222=+=AC ,︒=∠45BAC . ∵2213AC AD CD ===,,,∴222CD AC AD =+, ∴︒=∠90DAC ,∴︒=∠+∠=∠135BAC DAC DAB . 【总结】考察勾股定理及其逆定理的综合运用.【例19】 如图,已知在△ABC 中,∠B =90°,AB =BC ,AD 是BC 边上的中线,EF 是AD的垂直平分线,交AB 于点E ,交AC 于点F ,求AE :BE 的值. 【答案】5:3. 【解析】连接ED ,∵EF 是AD 的垂直平分线,∴ED AE = 设2==BC AB ,x ED AE ==,则x BE -=2∵222ED BD BE =+,∴()22212x x =+-,解得:45=x . 则434522=-=-=x BE , ABCD AB CD EF∴3:543:45:==BE AE . 【总结】考察勾股定理和线段垂直平分线性质的综合运用.【例20】 如图,∆ABC 是等边三角形,P 是三角形内一点,P A =3,PB =4,PC =5,求∠APB 的度数.【答案】150°.【解析】在BC 的下方作︒=∠60PBD ,在BD 上截取一点D ,使得BD=BP ,连接CD 、PD∵︒=∠+∠60PBC ABP ,︒=∠+∠60PBC DBC ∴CBD ABP ∠=∠∵BC AB =,CBD ABP ∠=∠,BP BD = ∴CBD ABP ≌△△,∴3==AP CD∵︒=∠60PBD ,BP BD =,∴△BPD 为等边三角形,∴4==BP DP . ∵435DP DC PC ===,,,∴222PC DC DP =+,∴︒=∠90PDC ∴︒=∠+∠=∠150PDC BDP BDC ∵CBD ABP ≌△△, ∴︒=∠=∠150BDC APB【总结】考察旋转辅助线的作法和勾股定理逆定理的应用.【例21】 如图,P 是凸四边形内一点,过点P 作AB 、BC 、CD 、DA 的垂线,垂足分别为E 、F 、G 、H ,已知AH =3,DH =4,DG =1,GC =5,CF =6,BF =4,且BE -AE =1, 求四边形ABCD 的周长. 【答案】34.【解析】由勾股定理可得:22222PE AE PH AH AP +=+=, 22222PF BF PE BE BP +=+=, 22222PG CG CF PF CP +=+=, 22222PH DH GP DG DP +=+=,等式相加后代入数据可得:2222222454163+++=+++AE BE ,ABCDEFGHPBAP CD整理得:2211BE AE -=,即()()11BE AE BE AE +-=,∵BE -AE =1, 解得:65BE AE ==,. 所以周长为:3415646534+++++++=. 【总结】考察勾股定理的应用,注意解题方法的合理选择.【例22】 已知,如图,在△ABC 中,∠ACB =90°,CD ⊥AB 于点D ,设AC =b ,BC =a ,AB =c ,CD =h . 求证:(1)c h a b +>+;(2)以a b +、c h +、h 为三边可构成一个直角三角形.【解析】(1)由等面积可知:ch ab =,∵222c b a =+,∴()ch c b ab a b a 222222+=++=+,()ch h c h c 2222++=+. ∵ch h c ch c 22222++<+,∴()()22h c b a +<+,∴c h a b +>+.(2)∵()ch h c h c 2222++=+;()ab b a h b a h 222222+++=++,222c b a =+,ch ab = ∴()()222b a h h c ++=+,∴以a b +、c h +、h 为三边可构成一个直角三角形.【总结】考察勾股定理及其逆定理的应用、等面积法的综合应用.3、 距离公式:如果平面内有两点11()A x y ,、22()B x y ,,则A 、B 两点间的距离为:221212()()x x y y -+-.(1) 当11()A x y ,、22()B x y ,两点同在x 轴上或平行于x 轴的直线上,则有12y y =,AB =12||x x -;(2) 当11()A x y ,、22()B x y ,两点同在y 轴上或平行于y 轴的直线上,则有12x x =,AB =12||y y -.例题解析模块三:两点间的距离公式知识精讲AB CD【例23】 已知点A (2,2)、B (5,1).(1) 求A 、B 两点间的距离; (2) 在x 轴上找一点C ,使AC =BC . 【答案】(1)10;(2)()30C ,. 【解析】(1)()()10125222=-+-=AB ;(2)设()0C x ,, ∵AC =BC ,∴()()22221522+-=+-x x ,3=x ,∴()30C ,. 【总结】考察两点之间距离公式的应用.【例24】 (1)已知A (x ,3)、B (3,x +1)之间的距离为5,则x 的值是_________;(2)已知点P 在第二、四象限的平分线上,且到Q (2,-3)的距离为5,则点P 的坐标为_________.【答案】(1)16-=或x ;(2)()66P -,或()11P -,. 【解析】(1)由题意有:()()513322=--+-x x ,∴16-=或x ;(2)设()a a P -,,∴()()53222=+-+-a a ,∴16-=或a ,∴()66P -,或()11P -,. 【总结】考察两点之间距离公式的应用.【例25】 (1)以点A (1,2)、B (-2,-1),C (4,-1)为顶点的三角形是________;(2)已知点A (0,3)、B (0,-1),△ABC 是等边三角形,则点C 的坐标是_______.【答案】(1)等腰直角三角形;(2)()1C 或()1C -.【解析】(1)∵233322=+=AB ,60622=+=BC ,233322=+=AC ,∴222BC AC AB =+,AC AB =, ∴该三角形为等腰直角三角形; (2)()C a b ,,(3)∵4=AB ,∴()4322=-+=b a AC ,()4122=++=b a BC ,解得:a =±,1b =,∴()1C 或()1C -. 【总结】考察两点之间距离公式的应用.【例26】 已知直角坐标平面内的点A (4,1)、B (6,3),在坐标轴上求点P ,使P A =PB . 【答案】()70P ,或()07P ,. 【解析】①当点P 在x 轴上时,设()0P x ,,∵P A =PB ,∴()()22223614+-=+-x x ,7=x ,∴()70P ,②当点P 在y 轴上时, 设()0P y ,,∵P A =PB ,∴()()22226341+-=+-y y ,7=y ,∴()07P ,∴满足条件的P 点的坐标为()70P ,或()07P ,. 【总结】考察两点之间距离公式的应用,由于点P 在坐标轴上,注意分类讨论.【例27】 已知直角坐标平面内的点P (4,m ),且点P 到点A (-2,3)、B (-1,-2)的距离相等,求点P 的坐标.【答案】845P ⎛⎫⎪⎝⎭,.【解析】由题意可知:()()22225263++=+-m m ,解得:58=m ,∴845P ⎛⎫ ⎪⎝⎭,.【总结】考察两点之间距离公式的应用.【例28】 已知点A (2,3)B (4,5),在x 轴上是否存在点P ,使得PA PB +的值最小?若存在,求出这个最小值;若不存在,说明理由. 【答案】存在,最小值为172.【解析】找出A (2,3)关于x 轴对称的点为()23C -,,连接BC ,则PA PB +的值最小值为1728222=+=BC . 【总结】考察两点之间距离公式的应用.【例29】 已知直角坐标平面内的点A (4,32)、B (6,3),在x 轴上求一点C ,使得 △ABC 是等腰三角形.【答案】10704C ⎛⎫⎪⎝⎭,或()60C ,或()20C ,. 【解析】设()0C x ,, 当CA =CB 时,∴()()222236234+-=⎪⎭⎫ ⎝⎛+-x x ,16107=x ,∴10704C ⎛⎫⎪⎝⎭,; 当CA =AB 时,∴()2222223234+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+-x ,62或=x ,∴()60C ,或()20C ,; 当CB =AB 时,∴()222222336+⎪⎭⎫ ⎝⎛=+-x ,方程无解,所以不存在.综上,满足条件的点C 的坐标为:10704C ⎛⎫⎪⎝⎭,或()60C ,或()20C ,. 【总结】考察两点之间距离公式的应用,注意分类讨论.【例30】 已知点A (4,0)、B (2,-1),点C 的坐标是(x ,2-x ),若△ABC 是等腰三角形,求C 的坐标.【答案】7322C ⎛⎫- ⎪⎝⎭,或662622C ⎛⎫++- ⎪ ⎪⎝⎭,或666222C ⎛⎫+- ⎪ ⎪⎝⎭,或()11C -,或()42C -,. 【解析】由两点间距离公式,可得:22(42)15AB =-+=,22(4)(2)AC x x =-+-,22(12)(2)BC x x =---+-.当CA =CB 时,即()()()()222221224x x x x +--+-=-+-,解得:27=x ,∴7322C ⎛⎫- ⎪⎝⎭,; 当CA =AB 时,即()()22221224+=-+-x x ,解得:266266-+=或x ,∴662622C ⎛⎫++- ⎪ ⎪⎝⎭,或666222C ⎛⎫+- ⎪ ⎪⎝⎭,;当CB =AB 时,即()()222221212+=+--+-x x ,解得:14x x ==或,所以()11C -,或()42C -,. 综上,满足条件的C 点的坐标为:7322⎛⎫- ⎪⎝⎭,或662622⎛⎫++- ⎪ ⎪⎝⎭,或666222⎛⎫+- ⎪ ⎪⎝⎭, 或()11-,或()42-,. 【总结】本题主要考察两点之间距离公式及勾股定理的应用,由于题目中并没有说明斜边是哪条边,因此要分类讨论.随堂检测【习题1】 六根细木棒,她们的长度分别是2、4、6、8、10、12(单位:cm )从中取出三根,首尾顺次连接搭成一个直角三角形,则这些木棒的长度分别为().A . 2、4、8B .4、8、10C .6、8、10D .8、10、12【答案】C【解析】只有C 答案满足勾股定理逆定理. 【总结】考察勾股定理逆定理的应用.【习题2】 已知点A (2,4)B (-1,-3)C (-3,-2),那么△ABC 的形状是()A .等腰三角形B .直角三角形C .等腰直角三角形D .以上都不是【答案】D【解析】∵587322=+=AB ,51222=+=BC ,616522=+=AC ,∴222BC AC AB ≠+,∴该三角形不是直角三角形,也不是等腰三角形. 【总结】考察两点之间的距离公式的应用.【习题3】 (1)如果等腰直角三角形一边长为2,另外两边长为_________;(2)如果直角三角形两边长为5和12,第三边长度为_______________. 【答案】(1)2,22或22,;(2)13或119.【解析】两题目中的边长可能为两直角边或一条直角边和一条斜边. 【总结】考察勾股定理的应用.【习题4】 如图,将长方形ABCD 沿AE 折叠,使得点D 落在BC 上的点F 处,AB =8,AD =10.求EC 的长. 【答案】3=CE .【解析】由翻折性质,可知:10==AF AD ,∴622=-=AB AF BF ,∴4610=-=-=BF BC CF . 设x DE EF x EC -===8,∵222EF CF CE =+,∴()22284x x -=+,解得:3=x .∴3=CE .A BCDEF【总结】考察勾股定理的应用.【习题5】 如图,在四边形ABCD 中,AB ⊥BC ,AB =9,BC =12,CD =15,DA =152.求四边形ABCD 的面积.【答案】2333.【解析】联结AC ,过C 作CE ⊥AD∵AB ⊥BC ,AB = 9,BC =12,∴15=AC .∵CD =15,15=AC ,152,∴222CD AC AD +=, ∴ACD 为直角三角形.∴1122ABC ADC ABCD S S S AB BC AD EC =+=⋅⋅+⋅⋅△△四边形111523339121522222=⨯⨯+⨯⨯=. 【总结】考察勾股定理及其逆定理的综合运用.【习题6】 如图,在△ABC 中,AD 为BC 边上的中线,AB =5,AC =3,AD =2.求:△ABC的面积. 【答案】6.【解析】延长AD 至E ,使得DF=AD ,联结CE∵CD BD =,CDE ADB ∠=∠,DF=AD , ∴CDE ABD ≌△△,∴5==CE AB∵345AC AE CE ===,,,∴222CE AE AC =+, ∴︒=∠90DAC ,∴321=⋅⋅=AC AD S ADC △. ∵CD BD =,∴62==ADC ABC S S △△.【总结】考察勾股定理逆定理的应用和等底同高的面积相等的应用.AB CDABDCE【习题7】 若A 、B 、C 是三角形的边长且关于x 的方程222()20x a b x c ab -+++=有两个相等的实数根,试判断这个三角形的形状.【答案】直角三角形.【解析】由题意可知:()[]()024222=+-+-ab c b a ,∴222c b a =+,∴这个三角形为直角三角形. 【总结】考察勾股定理逆定理的应用.【习题8】 如图,在一条公路上有P 、Q 两个车站,相距27km ,A 、B 是两个村庄,AP ⊥PQ ,BQ ⊥PQ ,且AP =15km ,BQ =24km ,现在要在公路上建立一个商场M 使得A 、B 两个村庄到商场M 的距离相等,求PM 的长 . 【答案】20=PM .【解析】设x MQ x PM -==27,,∵MB MA =,∴()2222242715+-=+x x ,解得:20=x , ∴20=PM .【总结】考察勾股定理的应用及对最小值的应用.【习题9】 已知点()()2814A B -,,,点C 在y 轴上,使ABC ∆为直角直角三角形,求满足条件的点C 的坐标.【答案】()066C +,或()066C -,或1902C ⎛⎫ ⎪⎝⎭,或1304C ⎛⎫⎪⎝⎭,. 【解析】设()0C y ,,则24(8)AC y =+-,21(4)BC y =+-,22345AB =+=.当222AB BC AC =+时,则()()222222431428+=+-++-y y , 解得:6666y y =+=-或,∴()066C +,或()066C -,; 当222BC AB AC =+时,则()()222222144328+-=+++-y y ,解得:219=y , ∴1902C ⎛⎫⎪⎝⎭,;当222AC AB BC =+时,则()()222222284314+-=+++-y y ,解得:413=y , ∴1304C ⎛⎫ ⎪⎝⎭,.∴综上所述,满足条件的C 点的坐标为:()066C +,或()066C -,或1902C ⎛⎫⎪⎝⎭,或 1304C ⎛⎫ ⎪⎝⎭,.【总结】考察两点之间的距离公式的运用,注意分类讨论.ABQPM【习题10】 如图,在ABC ∆中,90ACB AC BC M ∠==,,是ABC ∆内一点,且312AM BM CM ===,,,求BMC ∠的度数.【答案】135°.【解析】在过点C 作CD ⊥CM 于点C ,在CD 上截取一点D ,使得CD=CM ,连接BD∵︒=∠+∠90DCA ACM ,︒=∠+∠90BCM ACM ∴BCM DCA ∠=∠∵BC AC =,BCM DCA ∠=∠,CM CD = ∴BCM ACD ≌△△, ∴1==AD BM∵︒=∠90MCD ,CM CD =, ∴22=DM ,︒=∠45CDM ∵1223DA DM AM ===,,, ∴222AM DM DA =+, ∴︒=∠90ADM∴︒=∠+∠=∠135CDM ADM ADC ∵BCM ACD ≌△△, ∴︒=∠=∠135ADC BMC【总结】考察旋转辅助线的作法和勾股定理逆定理的应用.ABCMD【习题11】 若在△ABC 中,AB =c ,AC =b ,BC =a ,∠ACB =90°,则222a b c +=试用两种方法证明.【解析】方法一:如图,△CDE ≌△ADE ,且B 、C 、D 在一条直线上,联结AE∵△CDE ≌△ADE ,∴CED ACB ∠=∠∵︒=∠+∠90CED ECD ,∴︒=∠+∠90CED ACB ,∴︒=∠90ACE∴梯形ABDE 的面积为()()22121221c ab b a b a +⨯=++整理得:222a b c +=,即得证.方法二、如图,由四个△ABC 拼成以下图形, 则四边形BCEG 和四边形ADFH 都为正方形∵四边形BCEG 的面积为2c ,∴四边形ADFH 的面积为()22214b a c ab +=+⨯,整理得:222a b c +=,即得证.【总结】本题主要考查学生对勾股定理的理解及通过几何说理方法说明定理的正确性.【作业1】 下列命题中,正确的有()个(1) 腰长及底边上的高对应相等的两个等腰三角形全等 (2) 有一直角边和斜边对应相等的两个直角三角形全等 (3) 有两边和其中一边上的高对应相等的两个三角形全等 A .0 B .1 C .2 D .3【答案】C【解析】(1)(2)正确,(3)错误,分锐角三角形和钝角三角形两种情况.故选C . 【总结】考察三角形全等的判定.【作业2】 如图,图中的字母、数代表正方形的面积,则A =______. 【答案】22.【解析】根据勾股定理得A 的面积等于另外两正方形面积之差. 【总结】考察勾股定理的应用.【作业3】 如图,Rt ABC ∆中,斜边1AB =,则222AB BC AC ++的值是_________. 【答案】2.【解析】222=1+1=2AB BC AC ++. 【总结】考察勾股定理的应用.【作业4】 已知点()35A -,,点B 的横坐标为-3,且A 、B 两点之间的距离为10,那么点B 的坐标是____________. 【答案】()()33313B B ---,或,. 【解析】设()3B m -,,∵BA =10,∴()106522=++m ,解得:133-=或m ,∴()()33313B B ---,或,. 【总结】考察两点之间的距离公式的应用.【作业5】 现将直角三角形ABC 的直角边AC 沿直线AD 折叠,使它落在斜边AB 上,点C与点E 重合,已知AC =3,BC =4,则CD 等于_____________.课后作业5072A【答案】23=CD . 【解析】由翻折性质,可得:3==AE AC ,∴2=BE .设4CD DE x DB x ===-,则,∵222BD BE DE =+,∴()22242x x -=+,解得:23=x ,∴23=CD . 【总结】考察翻折性质及勾股定理的综合应用.【作业6】 如果ABC ∆的周长为12,而22AB BC AC AB BC +=-=,,那么ABC ∆的形状是____________.【答案】直角三角形.【解析】∵12=++AC BC AB ,22AB BC AC AB BC +=-=,, 联立方程,解得:534AB BC AC ===,,. ∵222CB AC AB +=,∴ABC ∆为直角三角形. 【总结】考察勾股定理逆定理的应用.【作业7】 已知等腰直角三角形ABC 斜边BC 的长为2,DBC ∆为等边三角形,那么A 、D两点的距离为_______. 【答案】13-=AD 或13+.【解析】∵CD BD AC AB ==,,∴DA 垂直平分BC .设DA 交BC 于E ,∵等腰直角三角形ABC 斜边BC 的长为2,∴1=AE∵DBC ∆为等边三角形,∴根据勾股定理和直角三角形的性质可得:3=DE 当A 点在DBC ∆内部时,13-=AD ; 当A 点在DBC ∆外部时,13+=AD .【总结】考察勾股定理和直角三角形的性质的综合运用,注意分类讨论.【作业8】 已知:如图,已知在Rt ABC ∆中,9030B C ∠=∠=,,将ABC ∆绕点A 逆时针旋转30后得到APQ ∆,若1AB =,则两个三角形重叠部分的面积为_________. 【答案】63.【解析】设AC 与PQ 相交于D由题意可得:︒=∠30BAO ,︒=∠30PAD ,1==AB AP ∵︒=∠90P ,︒=∠30PAD ,∴设2PD x AD x ==,ABCQPD∴()2221x x =+,解得:33=x . ∴6321=⋅⋅=PD AP S APD △. 【总结】考察勾股定理和直角三角形性质的综合运用.【作业9】 已知:如图,四边形ABCD 的三边(AB 、BC 、CD )和BD 都为5厘米,动点P 从A 出发(A B D →→),速度为2厘米/秒,动点Q 从点D 出发(D C B A →→→)到A ,速度为2.8厘米/秒,5秒后P 、Q 相距3厘米,试确定5秒时APQ ∆的形状. 【答案】直角三角形.【解析】P 点的运动路程为10厘米,则此时P 与D 重合;Q 点的运动路程为14厘米,此时BQ =4厘米. ∵534===BP PQ BQ ,,∴△BPQ 为直角三角形,且︒=∠90BQP ,即︒=∠90AQP . ∴APQ ∆的形状为直角三角形.【总结】考察动点背景下勾股定理逆定理的运用,注意对动点运动路线的判断.【作业10】 阅读下列题目的解题过程: 已知a 、b 、c 为ABC ∆的三边,且满足222244a c b c a b -=-,试判断ABC ∆的形状. 解:222244a c b c a b -=-(A ),()()()2222222c a b a b a b ∴-=+-(B ) 222c a b ∴=+(C ),∴ABC ∆是直角三角形.问:(1)上述解题过程中,从哪一步开始出错? 请写出该步的代号:____________; (2)错误的原因:_______________;(3)本题正确的结论为:____________.【答案】(1)C ;(2)两边同时除一个不为零的数,等式成立.(3)直角三角形或者等 腰三角形.【解析】C 步骤应该为:222220c a b a b =+-=或, 所以应为直角三角形或者等腰三角形.ABCDQP【总结】考察因式分解和勾股定理的综合应用.【作业11】 如图,一根长度为50CM 的木棒的两端系着一根长度为70CM 的绳子,现准备在绳子上找一点,然后将绳子拉直,使拉直后的绳子与木棒构成一个直角三角形,求满足条件的点有几个,并且这个点将绳子分成的两段各有多长?【答案】满足条件的点有2个,一段长为30厘米,一段长为40厘米. 【解析】设其中的一段长为x cm ,则另一段长为()cm x -70∴()2225070=-+x x ,解得:4030或=x .∴满足条件的点有2个,一段长为30厘米,一段长为40厘米. 【总结】考察勾股定理的应用,注意两个点的考虑.【作业12】 在直角坐标平面内,已知()()1054A B -,,,,在坐标轴上求一点P ,使得PAB ∆为直角三角形,求点P 的坐标. 【答案】()05P ,或()01P -,或302P ⎛⎫- ⎪⎝⎭,或2302P ⎛⎫ ⎪⎝⎭,或()50P ,或()10P -,或2303P ⎛⎫⎪⎝⎭,. 【解析】当点P 在y 轴上时,设()0P y ,, 当222AB BP AP =+,∴()22222246541+=+-++y y ,解得:15-=或y , ∴()05P ,或()01P -,; 当222BP AB AP =+,∴()22222254461+-=+++y y ,解得:23-=y ,∴302P ⎛⎫- ⎪⎝⎭,; 当222AP AB BP =+,∴()22222214654+=+++-y y ,解得:223=y ,∴2302P ⎛⎫⎪⎝⎭,;当点P 在x 轴上时,设()0P x ,, 当222AB BP AP =+,∴()()222222464501+=+-+++x x ,解得:15-=或x , ∴()50P ,或()10P -, 当222BP AB AP =+,∴()()222222454601+-=++++x x ,解得:1-=x ,∴()10P -,当222AP AB BP =+,∴()()222222014645++=+++-x x ,解得:323=x ,∴2303P ⎛⎫⎪⎝⎭,. 综上所述:满足条件的点P 的坐标为:()05P ,或()01P -,或302P ⎛⎫- ⎪⎝⎭,或2302P ⎛⎫⎪⎝⎭,或 ()50P ,或()10P -,或2303P ⎛⎫⎪⎝⎭,. 【总结】考察勾股定理的运用和两点之间的距离公式的综合应用,本题综合性较强,要进行多角度的分类讨论.。
两点之间距离公式距离是一个对象与另一个对象之间的空间间隔。
在数学中,我们使用距离公式来计算两个点之间的距离。
在平面几何中,我们通常使用欧几里得距离公式来计算两个点之间的距离。
欧几里得距离公式可以表示为:d=√((x2-x1)²+(y2-y1)²)其中,(x1,y1)表示第一个点的坐标,(x2,y2)表示第二个点的坐标,d表示两点之间的距离。
这个公式来自于勾股定理,也称为直角三角形的斜边长度。
它可以用来计算两点之间的直线距离。
这个公式的原理是基于欧几里得空间的平方距离公式,将平方根运算应用于平方和。
让我们通过一个实际的例子来说明这个公式的应用。
假设有两个点A 和B,它们的坐标分别是A(2,3)和B(5,6)。
我们可以使用欧几里得距离公式来计算它们之间的距离。
d=√((5-2)²+(6-3)²)=√(3²+3²)=√(9+9)=√18≈4.24所以,点A和点B之间的距离约为4.24个单位。
除了欧几里得距离公式,还有其他一些距离公式也常用于计算两点之间的距离,例如曼哈顿距离和切比雪夫距离。
曼哈顿距离公式可以表示为:d=,x2-x1,+,y2-y1它表示点A和点B之间的曼哈顿距离,也称为城市街区距离。
它是基于在城市街区内从一个点到达另一个点所需的最短距离。
切比雪夫距离公式可以表示为:d = max(,x2 - x1,, ,y2 - y1,)它表示点A和点B之间的切比雪夫距离,也称为棋盘距离。
它是基于在一个棋盘上从一个方格移动到另一个方格的最短距离。
距离公式在数学和科学领域中有广泛的应用,例如在计算机图形学中用于计算物体之间的距离,以及在机器学习算法中用于计算样本之间的相似性。
学科教师辅导讲义【答案】144【例10】如图,在一块用边长为cm20的正方形的地砖铺设的广场上,一只飞来的鸽子落在A点处,,鸽子吃完小朋友洒在B、C处的鸟食,最少需要走多远?【答案】360厘米【例11】欲登12米高的建筑物,为安全需要,需使梯子底端离建筑物5米,至少需多长的梯子?【答案】13米【例12】如图,有一个高是1.5米、半径是1米的圆柱形油桶,在上地面靠边的地方有一小孔,从孔中插入一根铁CBA棒,已知铁棒在油桶外的部分最短是0.5米,这根铁棒有多长?【答案】3米【例13】有一个圆柱,它的高等于12厘米,底面半径等于3厘米.在圆柱的下底面点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,需要爬行的最短路程是多少?( 的值取3)【分析】圆柱的侧面展开图是一个长方形.最短路线为展开图中的线段AB.【答案】15cm【例14】中国古代的数学家们不仅很早就发现并应用勾股定理,最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。
赵爽创制了一幅“勾股圆方图”,用形数结合的方法,给出了勾股定理的详细证明。
你能根据这幅“勾股圆方图”证明勾股定理吗?(图中4个直角三角形全等)【答案】在这幅“勾股圆方图”中,以弦为边长得到正方形ABDE是由4个全等的直角三角形再加上中间的那个小正方形组成的。
每个直角三角形的面积为ab/2;中间的小正方形边长为b-a,则面积为(b-a)2。
于是便可得如下的式子:【借题发挥】1.飞机在空中水平飞行,某一时刻刚好飞到一个男孩的头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,飞机每小时飞行多少千米?【答案】540千米2.如图,每个小方格都是边长为1的正方形,C(1)求图中格点四边形ABCD的面积和周长。
(2)求∠ADC的度数。
3.如图:设甲到岛上去探宝,登陆后先往东走8千米,又往北走2千米,遇到障碍后又向西走3千米,再折向北走6千米处往东一拐,仅1千米找到宝藏,问登陆点到探宝点的距离是多少?4.△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则是直角三角形吗?5.你能用下面的图形也来验证一下勾股定理吗?试一试!6.在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池中央有一根新生的芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.这个水池的深度和这个芦苇的长度各为多少?A BCabcS1S3S2ACabcS2S3BS1【答案】214尺;294尺 7.求四个水平放置的正方形的面积的和.(即求1234S S S S +++)题型四:两点间距离公式【例14】求下列两点间的距离:(1)()2,8A -和()3,4B -(2)()2,1C和()2,3D -(3)()3,2P -和()23,1Q(4)()5,2M -和()2,5N (5)()1,2E 和()3,2F -(6)()5,4G -和()5,9H -【答案】略【方法总结】利用公式【例15】已知三角形三个顶点的坐标,判断三角形的形状.(1)()1,1A --、()3,1B -、()3,2C(2)()2,1A -、()2,3B --、()4,1C -(3)()3,1A -、()3,3B --、()233,1C --(4)()2,5A 、()5,1B -、()2,1C --(5)()1,3A -、()1,2B -、()4,5C(6)()1,2A --、()2,1B -、()2,1C -【答案】略【例16】3.在角坐标平面内,已知A 、B 两点的坐标分别为()1,3-、()6,4,线段AB 的垂直平分线交x 轴于点P ,求点P 的坐标【答案】(3,0)【借题发挥】在直角坐标平面内,已知△OAB 是等边三角形,且O 、B 两点的坐标分别为()0,0、()4,0.(1)求点A 的坐标.(2)如果△OAB 内一点P 到三角形三边的距离都相等,求点P 的坐标.【答案】(1)()()2,23,2,23-;(2)22,33⎛⎫ ⎪⎝⎭,22,33⎛⎫- ⎪⎝⎭ 【随堂练习】填空题:1.在直角三角形中,两条直角边分别为5,12,则斜边上的高为 .2.若长方形的一条对角线与一边的差为1cm ,另一条边长3cm ,则这个长方形的面积等于 平方厘米.3.若3是关于x 的方程()22120x a x -++=的解,那么以3,a 为边的等腰三角形的面积为 . 4.如图所示,在△ABC 中,AD 是BC 边上的中线,且AD ⊥AB 于A ,10,8AC AB ==,如果将△ABD 绕点旋转180°,将交点A 转到点A '的位置,那么AA '= .5.如图,△ABC 为等边三角形,边长为4cm ,D 为BC 中点,DE ⊥AB ,垂足为E ,EF ∥BC 交AC 于F ,则△AEF 的周长是 .【答案】1.6013;2.12;3.3914或5114;4.6;5.12. 选择题:1.在△ABC 中,∠C =90°,∠A =30°,6BC cm =,则此三角形的周长为( )A.63;B.1263+;C.183;D.1863+.2.已知Rt △ABC 的三边都是整数,两条直角边长度的比是3:4,则斜边的长可能是( )A.9;B.10;C.12;D.14.3.已知()2,4P -,()4,2Q -下列各点中在线段PQ 垂直平分线上的点有( )①()1,1A ②()2,2B -③()1,1C --④()0,0DA.1个;B.2个;C.3个;D.4个.4.三角形三个内角的度数比为3:2:1,那么它的三条边的长度之比为( )A.3:2:1;B.3:2:1;C.2:3:1;D.9:4:1.5.已知直角三角形有一条直角边长11厘米,另外两条边的长度都是自然数,那么这个三角形的周长为( )A.120厘米;B.132厘米;C.144厘米;D.156厘米.【答案】DBB CB解答题:1.如图,在△ABC 中,,∠A =90°,AB AC =,BD 平分∠ABC 交AC 于点D ,若2AB cm =.求:AD 的长,2.在Rt △ABC 中,∠C =90°,中线AD 的长为7,中线BE 的长为4.求:AB 的长3.已知()2,3A -和()1,4B 在y 轴上找一点C ,使△ABC 为直角三角形.4.四边形中,∠A =60°,∠B =∠D =90°,2,1AB CD ==.(1)求BC 、AD 的长;(2)求四边形ABCD 的面积.【答案】1.(222)cm -;2.213;3.()()()()0,3,0,7,0,2,0,5-;4.332; 【课堂总结】【课后作业】1.如图所示,在平行四边形ABCD 中,BE ⊥CD 于E ,BF ⊥AD 于F ,∠ABC =120°,2,23BE cm BF cm ==,则平行四边形ABCD 的面积为 平方厘米.2.在△ABC 中,5,8AB cm AC cm ==,∠BAC =60°,则BC 的长为 cm .3.如图所示,在扇形AOB 中,4OA =,∠AOB =120°,那么阴影部分的面积等于 .4.已知弓形的高为4cm ,弦长为12cm ,则弓形所在圆的半径为 .5.在直角坐标平面内有()()()0,6,0,2,4,2A B C -三个点,则以这三个点为顶点的△ABC 是 三角形.【答案】1.8;2.7;3.163π-43;4.132;5.等腰直角; 选择题:1.以下列各组数为三边长的三角形中,不能组成三角形的是( )A.31,31,22+-;B.3.5,4.5,5;C.4,7.5,8.5;D.()221,2,11n n n n -+>.2.在直角三角形中,若斜边上的中线是奇数,一条直角边是偶数,则另一条直角边一定是( )A.偶数;B.奇数;C.自然数;D.以上结论都不对.3.在下列命题中,真命题有( )①有一个角等于另外两个角的差的三角熊是直角三角形;②有一条边的平方等于另外两条边的平方和的三角形是直角三角形;③三条边长分别为10,20,30的三角形是直角三角形;④三个外角的度数之比为3:4:5的三角形是直角三角形.A.4个;B.3个;C.2个;D.1个.4.在Rt △ABC 中,斜边上的中线17CD =,直角边16AC =,则直角边BC 的长等于( )A.30;B.32;C.33;D.34.5.若直角三角形三边a 、b 、c 满足整式3222230a a b ab ac bc b ++--+=则的形状为( )A.等腰三角形;B.等边三角形;C.等腰直角三角形;D.直角三角形.【答案】BDAAD解答题:1.如图,已知Rt △ABC 中,∠C =90°,点D 为AC 的中点,DE ⊥AB 于E .求证:222BE BC AE =+.2.如图,在△ABC 中,∠C =90°,6,8AC cm BC cm ==,以点C 为圆心,CA 的长为半径作弧,交斜边AB 于D .求AD 的长.3.如图,某船向正东航行,在A 处望见某岛C 在北偏东60°方向,前进6海里到B 点,此时又测得岛C 在北偏东30°方向,已知在该岛周围6海里内有暗礁,问若船继续向东航行,有无触礁危险,请说明理由.4.给出一组式子:32+42=52,82+62=102,152+82=172,242+102=262.…(1)你能发现上面式子的规律吗?请你用发现的规律,给出第5个式子;(2)请你证明你所发现的规律.5.在直角坐标平面内,已知△ABC 是直角三角形,且∠C =90°,点C 在x 轴上,A 、B 两点的坐标分别是()2,6、()10,2,求点C 的坐标.6.在直角坐标系内,已知△OAB 是等腰三角形,O 、A 两点的坐标分别为(0,0)、(3,4),点B 在x 轴上,求点B 的坐标.【答案】1.略;2.7.2cm ;3.有危险;4.略;5.()()4,0,8,0;6.()()()255,0,,0,5,0,6,06⎛⎫- ⎪⎝⎭二、综合提高练习1.如图甲是第七届国际数学教育大会(简称ICME ~7)的会徽,会徽的主体图案是由如图乙的一连串直角三角形演化而成的其中18732211=====A A A A A A OA Λ,如果把图乙中的直角三角形继续作下去,细心观察图形,认真分析各式,然后解答问题:A 1OA 2A 3A 4A 5A 6A 7A 8ICME-7 图甲 图乙;2121112==+S ,)( ;22,31)2(22==+S ;23,41)3(32==+S …… (1) 请用含有n (n 是正整数)的等式表示上述变化规律;(2) 推算出OA 10的长;(3) 求出210232221S S S S ++++Λ的值。