当前位置：文档之家 › 空间直角坐标系 空间两点间的距离公式(解析版)

空间直角坐标系 空间两点间的距离公式(解析版)

  • 格式：doc
  • 大小：98.00 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

空间直角坐标系、空间两点间的距离公式 课件

空间直角坐标系、空间两点间的距离公式 课件
4.空间中的中点坐标公式 在空间直角坐标系中，若A(x1，y1，z1)，B(x2，y2，z2)，则
线段AB的中点坐标是_x_1_＋2__x_2，__y_1_＋_2_y_2_，__z1_＋2__z_2_.
类型一 求空间中点的坐标 【例1】 建立适当的坐标系，写出底边长为2，高为3的正三 棱柱的各顶点的坐标.
|MN|＝
32－12＋（3－1）2＋（1－2）2＝
21 2.
解 以BC的中点为原点，BC所在的直线为y轴，以射线 OA所在的直线为x轴，建立空间直角坐标系，如图. 由题意知，AO＝ 23×2＝ 3，从而可知各 顶点的坐标分别为 A( 3，0，0)，B(0，1，0)， C(0，－1，0)，A1( 3，0，3)，B1(0，1，3)，C1(0，－1，3).
类型二 求空间中对称点的坐标 【例2】 在空间直角坐标系中，点P(－2，1，4).
空间直角坐标系 空间两点间的距离公式
1.空间直角坐标系 (1)空间直角坐标系及相关概念 ①空间直角坐标系：从空间某一定点引三条两两垂直，且有相 同 单 位 长 度 的 数 轴 ： __x_轴__、__y轴__、__z_轴__ ， 这 样 就 建 立 了 一 个 __空__间__直__角__坐__标__系__O_－__x_y_z_. ②相关概念：__点__O_叫做坐标原点，x_轴__、__y_轴__、__z_轴_叫做坐标轴.通 过____每__两__个__坐__标__轴___的平面叫做坐标平面，分别称为_x_O__y_平 面、_y_O__z _平面、__zO__x_平面.
(1)求点P关于x轴的对称点的坐标； (2)求点P关于xOy平面的对称点的坐标； (3)求点P关于点M(2，－1，－4)的对称点的坐标.
解 (1)由于点P关于x轴对称后，它在x轴的分量不变， 在y轴、z轴的分量变为原来的相反数，所以对称点为 P1(－2，－1，－4). (2)由于点P关于xOy平面对称后，它在x轴、y轴的分量 不变，在z轴的分量变为原来的相反数，所以对称点为 P2(－2，1，－4). (3)设对称点为P3(x，y，z)，则点M为线段PP3的中点， 由中点坐标公式，可得x＝2×2－(－2)＝6， y＝2×(－1)－1＝－3，z＝2×(－4)－4＝－12， 所以P3(6，－3，－12).

空间中两点的距离公式

空间中两点的距离公式
P
M1
Q
y
O
因为 x | M1M2 | 2 = | M1Q | 2 + | M2Q | 2 = | M1P | 2 + | PQ | 2 + | M2Q | 2 所以 d | M1M2 |
( x2 x1 ) ( y2 y1 ) ( z 2 z1 )
2 2
2
例1 求证以M 1(4，3，1)、M 2(7，1，2)、M 3(5，2，
1、设 O(0,0,0),P(x0,y0,z0)
z P C y B
则
OP OA OB OC x y z
2 0 2 0 2 0 2 2 2
A
x
o
二、空间两点间的距离
作一个以M 1和M 2为对 角线顶点的长方体，使 其三个相邻的面分别平 行于三个坐标面．
设M 1(x 1，y 1，z 1)、M 2(x 2，y 2，z 2)为空间两点． z
z1
P
M1 Q
y
O x
设M 1(x 1，y 1，z 1)、M 2(x 2，y 2，z 2)为空间两点．
作一个以 M 1 和 M 2 为 对角线顶点的长方体，使 其三个相邻的面分别平行 于 三 个 坐 标 面 ．
z
M2
与x 轴平行的边的边长为|x 2x 1|，
与y 轴平行的边的边长为|y 2y 1|， 与z 轴平行的边的边长为|z 2z 1|．
坐标面： 三条坐标轴中的任意两 条可以确定一个平面，这样 定出的三个平面统称为坐标 面．x轴及y轴所确定的坐标
z
面叫做 xOy面，另两个坐标
面是 yOz 面和zOx面.
O
y
x
坐标面：
三条坐标轴中的任意两

空间两点间距离公式

空间两点间距离公式

距离公式？
z
1、设
O(0,0,0),P(x0,y0,z0)
则
OP
o A
OA 2 OB 2 OC 2 x
P C y
B
x02 y02 z02
2、空间任意两点A(x1,y1,z1),P(x2,y2,z2)
作长方体使AP为 长方体的对角线
z
由已知得： C(x2,y1,z1),
P A
B(x2,y2 ,z1)
x 1, 所求点 (1,0,0), (1,0,0). 为
例4.平面上到坐标原点的距离为１的点的
轨迹是单位圆，其方程
为 x2 y2 1
．
在空间中，到坐标原点的距离为１
的点的轨迹是什么？试写出它的方程．
x2 y2 z2 1
轨迹是球面
练3:设A(3,3,1),B(1,-1,5),C(0,1,0),则AB
的中点M到C的距离为____1_3____
分析：介绍空间直角坐标系中的中点坐标 公式；
已知点A(x1,y1,z1),点B(x2,y2,z2) 则线段AB中点C的坐标是
X= 1 (X1+X2)
2 1
Z= 2 (z1+z2)
y=
1 2
(y1+y2)
M(2,1,3)
例5：如图：M—OAB是棱长为a的正四 面体，顶点M在底面OAB上的射影为H， 分别求出点B、H、M的坐标
(9,0,0)或(-1,0,0)
例２：在xoy平面内的直线x+y=1上确定 一点M，使M到N(6,5,1)的距离最小 略解：设M(x,1-x,0),利用距离公式构造 出一个二次函数后求最值
MN (x 6)2 (1 x 5)2 (1 0)2

空间坐标系两点间距离公式

空间坐标系两点间距离公式

空间坐标系两点间距离公式设点A的坐标为(x1,y1,z1)，点B的坐标为(x2,y2,z2)。

利用勾股定理，我们可以得到两点之间的距离d：d=√((x2-x1)²+(y2-y1)²+(z2-z1)²)这个公式就是空间坐标系中两点之间距离的一般公式。

下面我们将对这个公式进行详细解释：首先，我们可以将(x2-x1)²简化为(x2-x1)*(x2-x1)。

同样，(y2-y1)²可以简化为(y2-y1)*(y2-y1)，(z2-z1)²可以简化为(z2-z1)*(z2-z1)。

接下来，我们将这些简化后的表达式相加，得到：d=√((x2-x1)²+(y2-y1)²+(z2-z1)²)=√((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1)+(z2-z1)*(z2-z1))我们可以继续简化这个表达式，将每个乘法展开：d=√(x2²-2*x1*x2+x1²+y2²-2*y1*y2+y1²+z2²-2*z1*z2+z1²)现在，我们可以对这个表达式进行合并和化简。

首先，我们可以将常数项合并：d=√(x2²+y2²+z2²+x1²+y1²+z1²-2*x1*x2-2*y1*y2-2*z1*z2)然后，我们注意到这个表达式中存在三个平方项，我们可以将它们重新组合：d=√((x2²+y2²+z2²)+(x1²+y1²+z1²)-2*x1*x2-2*y1*y2-2*z1*z2)接下来，我们可以使用公式(a + b)² = a² + 2ab + b²，将表达式中的求和项写成平方的形式：d=√(x2²+2*x1*x2+x1²+y2²+2*y1*y2+y1²+z2²+2*z1*z2+z1²-2*x1*x2-2*y1*y2-2*z1*z2)再次合并和化简，我们可以得到：d=√((x2+x1)²+(y2+y1)²+(z2+z1)²-2*(x1*x2+y1*y2+z1*z2))这个公式更简洁，而且计算起来更方便。

空间两点间距离公式

空间两点间距离公式

d x y02 z02 y d y x02 z02
d z x02 y02
两点间距离公式
平面：| P1P2 | (x1 x2 )2 ( y1 y2 )2
类比
猜想
空间：| P1P2 | (x1 x2 )2 ( y1 y2 )2 (z1 z2 )2
例4:已知 A( 3,3,3 2), B( 3,1, 2) ，在平面 Oyz上是否存在一点C，使ABC为等边三角 形，如果存在求C坐标，不存在说明理由。
解:假设存在一点C(0,y,z)，满足条件：
AB AC BC

3
3 2 3 12 3 2
2
2

y
3
0 2
C 0,4, 2 或 0,0,3 2
所以存在一点C，满足条件.
课堂小结
一、空间两点间的距离公式：
d ( x2 x1 )2 ( y2 y1 )2 (z2 z1 )2
二、空间中点坐标公式：

x

y
ห้องสมุดไป่ตู้

z

x1 y1 z1
x2
2 y2
2 z2
2
AC 1 32 5 12 2 52 29
例1:已知三角形的三个顶点A(1,5,2)， B(2,3,4)，C(3,1,5)，求: (2)BC边上中线AM的长。
AM ?
例2:求证以 M1(4,3,1), M2(7,1,2), M3(5,2,3), 三点为顶点的三角形是一个等腰三角形. 解: M1M2 2 (7 4)2 (1 3)2 (2 1)2 14,
4.3.2 空间两点间的距离公式

解析几何中两点间距离公式

解析几何中两点间距离公式

解析几何中两点间距离公式欢迎来到解析几何的世界。

你是否曾经在求两点间距离时使用过勾股定理？如果这还是你的唯一方法，那么我建议你应该试试使用解析几何中的公式来求解两点间的距离。

在此，我将会向你介绍两点距离公式以及它的相关内容。

让我们开始吧！一、什么是两点间距离公式？两点间距离公式，是解析几何中用于计算两个点之间距离的公式。

它可以用于二维平面和三维空间中。

在二维平面中，两点间距离公式被表示为：d = √ ((x2 - x1)² + (y2 - y1)²)其中，d为两点之间的距离，(x1, y1)和(x2, y2)是平面上的两个点。

在三维空间中，两点间距离公式被表示为：d = √ ((x2 - x1)² + (y2 - y1)² + (z2 - z1)²)其中，d为两点之间的距离，(x1, y1, z1)和(x2, y2, z2)是空间中的两个点。

二、两点间距离公式的推导过程在计算两点间距离公式的推导过程中，我们使用了勾股定理（两边平方，然后开方），从而得到了该公式。

我们将在下面详细讲解推导过程。

二维平面:为了推导两点间距离公式，在平面上我们假设有两个点A和B。

如下图所示：我们可以通过画一个直角三角形来计算AB之间的距离。

我们可以看出，点A和点B之间的距离等于C点到直角三角形的对角线长度。

如下图所示：根据勾股定理，我们可以得出方程：C² = A² + B²其中，C为对角线的长度，A和B为直角三角形两条边的长度。

将上述方程稍加变换后，可以得出两点之间的距离公式：d = √ ((x2 - x1)² + (y2 - y1)²)三维空间：在三维空间中，我们同样假设有两个点A和B。

与二维平面的情况类似，我们可以通过画一个直角三角形来计算AB之间的距离。

如下图所示，假设我们要计算点A和点B之间的距离。

我们可以通过勾股定理来计算AB之间的距离。

测量坐标计算公式大全

测量坐标计算公式大全

测量坐标计算公式大全一、两点间距离公式（平面直角坐标系）设两点坐标分别为A(x_1,y_1)，B(x_2,y_2)，则两点间的距离d为：d = √((x_2 - x_1)^2+(y_2 - y_1)^2)例如，A(1,2)，B(4,6)，则x_1 = 1,y_1=2,x_2 = 4,y_2 = 6d=√((4 - 1)^2+(6 - 2)^2)=√(3^2 + 4^2)=√(9+16)=√(25) = 5二、中点坐标公式（平面直角坐标系）设两点坐标分别为A(x_1,y_1)，B(x_2,y_2)，则AB中点M的坐标为(x_m,y_m)，其中。

x_m=(x_1 + x_2)/(2)y_m=(y_1 + y_2)/(2)例如，A( - 2,3)，B(4,-1)，则中点M的坐标为。

x_m=(-2+4)/(2)=1y_m=(3+(-1))/(2)=1即中点M(1,1)三、直线的斜率公式（平面直角坐标系）设直线上两点坐标为A(x_1,y_1)，B(x_2,y_2)（x_1≠ x_2），则直线AB的斜率k 为：k=(y_2 - y_1)/(x_2 - x_1)例如，A(1,2)，B(3,6)，则k=(6 - 2)/(3 - 1)=(4)/(2)=2四、直线的点斜式方程（平面直角坐标系）已知直线过点(x_0,y_0)，斜率为k，则直线方程为y - y_0=k(x - x_0)例如，直线过点(1,3)，斜率k = 2，则直线方程为y-3 = 2(x - 1)，即y=2x+1五、平面直角坐标系中坐标旋转公式。

设点P(x,y)绕原点旋转θ角后得到点P'(x',y')x'=xcosθ - ysinθy'=xsinθ + ycosθ六、极坐标与直角坐标的转换公式。

1. 直角坐标(x,y)转换为极坐标(ρ,θ)ρ=√(x^2 + y^2)θ=arctan(y)/(x)(x≠0)2. 极坐标(ρ,θ)转换为直角坐标(x,y)x = ρcosθy=ρsinθ七、空间直角坐标系中两点间距离公式。

第6章 多元函数微分学

第6章 多元函数微分学

6.4 多元复合函数微分法 6.4.1 多元复合函数微分法 设 z = f (u,v), u = u (x,y), v = v(x,y),则 , ∂z ∂f ∂u ∂f ∂v ∂z ∂f ∂u ∂f ∂v = ⋅ + ⋅ = ⋅ + ⋅ , ∂x ∂u ∂x ∂v ∂x ∂y ∂u ∂y ∂v ∂y 这是本节最重要、最好记忆的公式, 这是本节最重要、最好记忆的公式,也是应 用时最容易出错的公式.只要你不偷懒的话, 用时最容易出错的公式.只要你不偷懒的话,你 是不会出错的. 是不会出错的. 本节假设所有的抽象函数总能 满足所需要的条件. 满足所需要的条件. 的偏微商. 练习 求 z = (x2 + y2)xy 的偏微商. 提示： 提示：令u = x2 + y2, v = xy.
∂z ∂z dz = dx + dy ∂x ∂y
的偏微商与全微分. 例 求z = cos2x + 3siny的偏微商与全微分 的偏微商与全微分 ∂z ∂z 解 = −2sin 2x, = 3cos y. ∂x ∂y
∂z ∂z dz = dx + dy ∂x ∂y
= − 2sin2xdx + 3cosydy
第6章 多元函数微分学
重点： 重点：求偏微商 难点： 难点：多元复合函数微分法 多元函数极值
6.1 空间解析几何
6.1.1 空间直角坐标系
点与坐标
两点间的距离公式 间的距离公式： 间的距离公式：
d = (x1 − x2 ) + ( y1 − y2 )
2
2
间的距离公式： 间的距离公式：
d = (x1 − x2 ) + ( y1 − y2 ) + (z1 − z2 )

《空间两点的距离距离公式》

《空间两点的距离距离公式》

z
( x1, y1, z1 )
p2 ( x , y , z ) 2 2 2
B( x2 , y2 , z1 )
O
x2
p1
y1
A
y2
y
x1
R ( x2 , y2 ,0)
x
Q ( x1 , y1 ,0)
在空间直角坐标系中，点 和 p2 ( x2 , y2 , z2 ) 点的距离
P 1 ( x1 , y1 z1 )
2 2
d a b c
问题2：在空间直角坐标系中原点O（0，0，0） 到空间任意点P（x0，y0，z0）的距离，怎么求？
z d P ( x0 , y0 , z0 ) B (0, y0 ,0) y
p1 ( x , y ,0)
0 d
x y z
2 0 2 0
2 0
练3:设A(3,3,1),B(1,-1,5),C(0,1,0),则AB 的中点M到C的距离为_________ 13 分析：介绍空间直角坐标系中的中点坐标 公式；
已知点A(x1,y1,z1),点B(x2,y2,z2) 则线段AB中点C的坐标是
1 X= (X1+X2) 2 1 Z= 2 (z1+z2)
d ( x 2 x1 ) ( y2 y1 ) ( z 2 z1 )
2 2
2
公式的记忆方法：同名坐标差的平方和的算术根
例１ 求空间两点Ａ（３，－２，５ ） Ｂ（６，０，－１）的距离ＡＢ
练1：P(1,2,-2)和Q(-1,0,-1)的 3 距离是________ 练2：给定空间直角坐标系，在x轴上找 一点P，使它与点P0(4,1,2) 距离为 30 分析：设P(x,0,0),由已知求得x=9或-1 (9,0,0)或(-1,0,0)

空间两点间的距离公式

空间两点间的距离公式

类比
猜想
空 间 ： | P 1 P 2 | =( x 1 - x 2 ) 2 + ( y 1 - y 2 ) 2 + ( z 1 - z 2 ) 2 .
二、空间中点坐标公式
在空间直角坐标系中，点P(x1,y1,z1)和点
Q(x2,y2,z2)的中点坐标(x,y,z):
x
y
z
x1 x2 2
y1 y2 2
4．已知点P在z轴上满足|OP|=1（O是坐标原点）， 则点P到点A(1，1，1)的距离是___2_或___6__. 5．正方体不在同一平面上的两个顶点的坐标分别 为A(-1，2，-1)，B(3，-2，3)，则正方体的棱长 为__4___.
一、两点间距离公式
平 面 ： | P 1 P 2| =( x 1-x 2) 2+ ( y 1-y 2) 2 ，
z
x1 x2 , 2
y1 y2 , 2
z1 z2 . 2
例1 求证以M1(4,3,1)、M2(7,1,2)、M3(5,2,3)三点 为顶点的三角形是一个等腰三角形.
证明: M 1 M 2 2 = (7 4 )2 (1 3 )2 (2 1 )2 1 4 ,
M 2 M 3 2 = (5 7 )2 (2 1 )2 (3 2 )2 6 ,
4.3.2 空间两点间的距离公式
2006年3月俄罗斯空军特 技飞行表演队在我国著名风 景区张家界市天门山进行特 技表演．
为了保证安全飞行，飞 行员及地面指挥员们如何准 确确定飞机之间的距离？
1. 在平面直角坐标系中两点间的距离公式是什么？ | P1P2 | (x1 - x2 )2 (y1 - y2 )2
z1 z2 2
不要害怕批评。当你提出新的观念时， 就要准备接受别人的批评。

空间直角坐标系空间两点间的距离公式

空间直角坐标系空间两点间的距离公式

【质疑探究 2】 空间中线段的中点坐标如何 表示? (设 M(x1,y1,z1),N(x2,y2,z2)是空间中两点,则
线段 MN 的中点 P 的坐标为( x1 x2 , y1 y2 ,
2
2
z1 z2 ))
2
(1)点 P(2,-4,2)与点
O(0,0,0)的中点坐标为
.
(2)空间直角坐标系中,点 A(-3,4,0)和点
(( x1 x2 , y1 y2 , z1 z2 ))
2
2
2
解:如图所示,分别以 AB,AD,AA1 所在的直线 为 x 轴、y 轴、z 轴建立空间直角坐标系. 由题意可知 C(3,3,0),D(0,3,0), ∵|DD1|=|CC1|=|AA1|=2, ∴C1(3,3,2),D1(0,3,2), ∵N 为 CD1 的中点,
课前预习
栏 目
导
航
课堂探究
【课标要求】
1.理解空间直角坐标系的有关概念,会根据 坐标描出点的位置、由点的位置写出点的 坐标. 2.掌握空间两点间的距离公式,理解公式使 用的条件,会用公式计算或证明.
【实例】我们知道了把几何问题放在坐标系中 研究,就可以得到一些数据,利用代数的方法研 究几何问题,对正方形 ABCD,边长为 2,建立一个 合适的坐标系后(如图所示可以得到 A(0,0), B(2,0),C(2,2),D(0,2)).
空间直角坐标系
1:要想给一个棱长为 2 的正方体 标注坐标,可以怎样建立坐标系呢? (可以建立空间直角坐标系)
1:(1)空间直角坐标系
如图,为了确定空间点 的位置,我们建立空间 直角坐标系:以正方体 为载体,以 O 为原点,分 别以射线 OA,OC,OD′ 的方向为正方向,以线段 OA,OC,OD′的长为单 位长,建立三条数轴:x 轴、y 轴、z 轴,这时我

北师大版必修2高中数学第2章解析几何初步33.3空间两点间的距离公式

北师大版必修2高中数学第2章解析几何初步33.3空间两点间的距离公式

思考：空间两点间的距离公式与平面两间点的距离公式的区别与 联系？
提示：平面两点间的距离公式是空间两点间的距离公式的特例： ①在平面直角坐标系 xOy 中，已知两点 A(x1，y1)，B(x2，y2)，则|AB| ＝ x1－x22＋y1－y22；②在 x 轴上的两点 A，B 对应的实数分别是 x1，x2，则|AB|＝|x2－x1|.
1．空间直角坐标系中，点 A(－3,4,0)和点 B(2，－1,6)的距离是
() A．2 43
B．2 21
C．9
D. 86
D [|AB|＝ －3－22＋4＋12＋0－62＝ 86.]
2．在空间直角坐标系中，设 A(1,2，a)，B(2,3,4)，若|AB|＝ 3，
则实数 a 的值是( )
A．3 或 5
【例 2】 已知 A(x,5－x,2x－1)，B(1，x＋2,2－x)，求|AB|取最 小值时 A、B 两点的坐标，并求此时的|AB|.
[思路探究] 解答本题可由空间两点间的距离公式建立关于 x 的 函数，由函数的性质求 x，再确定坐标．
[解] 由空间两点的距离公式得|AB|＝
1－x2＋[x＋2－5－x]2＋[2－x－2x－1]2
＝ 14x2－32x＋19
＝ 14x－872＋57， 当 x＝87时，|AB|有最小值
75＝
35 7.
此时 A87，277，79，B1，272，67.
解决这类问题的关键是根据点的坐标的特征，应用空间两点间的 距离公式建立已知与未知的关系，结合已知条件确定点的坐标.
2．在空间直角坐标系中，已知 A(3,0,1)，B(1,0，－3)．在 y 轴上 是否存在点 M，使△MAB 为等边三角形？若存在，求出点 M 的坐标； 若不存在，说明理由．

用4.3.2空间两点间的距离公式

用4.3.2空间两点间的距离公式
解：以底面中心作为坐标原点O，建立如图所示坐标系， 则P1P2⊥y轴，P1P4⊥x轴，SO在z轴上，且P1、P2、P3、P4 均在xOy平面上. ∵正四棱锥的所有棱长为a， a a a a 0) . ∴P1 ( ， ， 0) ，P2 ( ， ，
2 2
2 2
∵P3与P1关于原点O对称，P4与P2关于原点O对称.
dx dy dz
y z
2 0
2 0 2 0 2 0
O x
x z
2 0 2 0
x y
规律：谁没有，就等于谁.
练 5 ．点P(2,3,5)到平面xOy的距离为________ ． 1. 习 5
[解析]
d＝|z|＝5.
6．已知点M到三个坐标平面的距离都是1，且点M的三个 2.
[答案] ．(1,1,1)或(－1，－1，－1) 坐标同号，则点M的坐标为________
3 解： M的坐标为 (4, ,5) 2 5 N的坐标为 (4,3, ) 2
(0,0,5) (4,0,5) (4,3,5)
(0,3,5)
3 AC与BO交点的坐标 (2, ,0) 2
3 5 AC1与A1C的交点的坐标 (2, , ) 2 2
(0,3,0)
(0,0,0)
(4,0,0) (4,3,0)
练 7.如图所示，在棱长为1的正方体ABCD-A1B1C1D1中，E、F分别为D1D、BD的 1 习 中点，G在棱CD上，且CG= CD，H为C1G的中点，试建立适当的坐标系， 写出E、F、G、H点的坐标. 4 z (0,0,1) 解:如图所示,以D为原点,DA所在直线为x 轴,DC所在直线为y轴,DD1所在直线为z轴 建立空间直角坐标系. (1,0,1)
(2)求EF的长．

直角坐标系两点之间距离公式

直角坐标系两点之间距离公式

直角坐标系两点之间距离公式
直角坐标系中，两点之间的距离可以使用以下公式进行计算：
d = √((x2 - x1)^2 + (y2 - y1)^2)
其中，点1的坐标为(x1, y1)，点2的坐标为(x2, y2)。

这个公式也被称为欧几里德距离公式或直线距离公式。

它可以用
来计算两个平面上的点之间的直线距离。

除了直角坐标系中的点，这个公式也可以用于其他坐标系，比如
极坐标系或球坐标系。

只需将坐标系中的点的坐标转换成直角坐标系
的坐标，然后使用上述公式计算距离即可。

需要注意的是，此公式只适用于二维平面。

如果是三维空间中的点，则需要使用三维空间中两点之间的距离公式：
d = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)
其中，点1的坐标为(x1, y1, z1)，点2的坐标为(x2, y2, z2)。

如果要计算更高维度空间中两点之间的距离，可以使用m维空间中两点之间的距离公式：
d = √((x2 - x1)^2 + (y2 - y1)^2 + … + (mi - ni)^2)
其中，点1的坐标为(x1, y1, …, n1)，点2的坐标为(x2,
y2, …, n2)。

这个公式可以推广到任意维度的空间。

但在现实生活中，常用的是二维和三维空间的距离计算。

空间两点间的距离公式

空间两点间的距离公式
2 2
2
一、空间两点间的距离公式
在空间中，设点P1（x1，y1，z1），P2（x2， y2，z2）在xOy平面上的射影分别为M、N.
z
O x P1 N y P2
M
思考1:点M、N之间的距离如何？
MN
x1 x2
2
y1 y2
2
思考2:若直线P1P2 是xOy平面的一条 斜线，则点P1、P2的距离如何计算？
例2
设 P 在 x 轴上，它到 P1 ( 0, 2 ,3) 的距离为
到点 P2 ( 0,1,1) 的距离的两倍，求点 ， P在
PP1 PP2
x
2
2

2
3
2

x 2 11 , x2 2,
2 x 2 1 12
2 2
∴点 M
23 的坐标为0， 4 ，0.
小结
一、空间两点间的距离公式：
d ( x 2 x1 ) ( y2 y1 ) ( z 2 z1 )
2 2
2
二、空间中点坐标公式：
x1 x2 x 2 y1 y2 y 2 z1 z2 z 2
例 1 求证以 M 1 ( 4,3,1)、 M 2 ( 7,1,2)、 M 3 (5,2,3) 三点为顶点的三角形是一个等腰三角形.
解 M 1 M 2 (7 4)2 (1 3)2 ( 2 1)2 14,
2
M 2 M 3 (5 7)2 ( 2 1)2 ( 3 2)2 6, M 3 M1
z
P1 O x P2
A
y
M
N
P1 P2
x1 x2

空间直角坐标系公式

空间直角坐标系公式

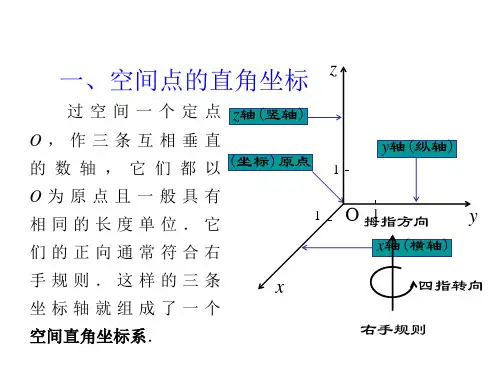
空间直角坐标系公式引言：空间直角坐标系是描述空间中点位置的常用工具，它通过三个相互垂直的坐标轴来确定一个点的位置。

本文将介绍空间直角坐标系的公式及其应用。

一、空间直角坐标系的定义空间直角坐标系是由三个相互垂直的坐标轴组成，分别是x轴、y 轴和z轴。

这三个轴的交点被定义为原点O，它们的方向和长度可以任意确定。

二、空间直角坐标系的公式在空间直角坐标系中，每个点的位置可以通过三个坐标值来表示，分别是x坐标、y坐标和z坐标。

假设某点的坐标为(x, y, z)，那么它与坐标轴的关系可以通过以下公式来表示：1. x轴上的投影：P(x, 0, 0)2. y轴上的投影：P(0, y, 0)3. z轴上的投影：P(0, 0, z)4. 坐标原点O：P(0, 0, 0)三、空间直角坐标系的应用空间直角坐标系广泛应用于物理学、几何学和工程学等领域。

下面将介绍一些常见的应用。

1. 点的距离计算在空间直角坐标系中，两点之间的距离可以通过勾股定理来计算。

假设两点分别为A(x1, y1, z1)和B(x2, y2, z2)，它们之间的距离d 可以通过以下公式计算：d = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)2. 点的中点计算在空间直角坐标系中，两点之间的中点坐标可以通过以下公式计算：中点坐标 = ((x1 + x2) / 2, (y1 + y2) / 2, (z1 + z2) / 2)3. 点的划分比例计算在空间直角坐标系中，可以通过给定两点和一个比例来计算划分点的坐标。

假设两点为A(x1, y1, z1)和B(x2, y2, z2)，要求划分比例为m:n，划分点的坐标为P(x, y, z)。

可以通过以下公式计算：x = (mx2 + nx1) / (m + n)y = (my2 + ny1) / (m + n)z = (mz2 + nz1) / (m + n)4. 直线的方程计算在空间直角坐标系中，可以通过给定一点和一个方向向量来计算直线的方程。

坐标系中两点距离怎么求

坐标系中两点距离怎么求

坐标系中两点距离的求解方法引言在坐标系中，我们经常需要计算两个点之间的距离，无论是平面坐标系还是三维坐标系。

求解两点间的距离可以应用于众多领域，包括数学、物理学、经济学等。

本文将介绍如何计算坐标系中两点之间的距离。

平面坐标系中两点距离的求解方法假设平面坐标系中有两个点A和B，坐标分别为A(x1, y1)和B(x2, y2)。

方法一：欧氏距离公式欧氏距离是在几何空间中常用的距离度量方法，可以用来计算平面坐标系中两点之间的距离。

欧氏距离公式如下：d = √((x2 - x1)^2 + (y2 - y1)^2)其中，d表示两点之间的距离。

方法二：勾股定理在三角学中，勾股定理可以用来计算两条直角边的长度，也可以用来计算平面坐标系中两点之间的距离。

根据勾股定理，可得：d = √((x2 - x1)^2 + (y2 - y1)^2)与欧氏距离公式相同。

三维坐标系中两点距离的求解方法假设三维坐标系中有两个点A和B，坐标分别为A(x1, y1, z1)和B(x2, y2, z2)。

方法一：欧氏距离公式在三维空间中，欧氏距离公式依然适用于计算两点之间的距离。

欧氏距离公式如下：d = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)其中，d表示两点之间的距离。

方法二：空间直角坐标系下的勾股定理在三维空间中，我们可以将两点之间的距离表示为三个坐标方向上的长度的平方和的平方根。

根据勾股定理，可得：d = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)与欧氏距离公式相同。

结论本文介绍了在平面坐标系和三维坐标系中求解两点之间距离的方法。

对于平面坐标系，我们可以使用欧氏距离公式或勾股定理来求解；而对于三维坐标系，同样可以使用欧氏距离公式或空间直角坐标系下的勾股定理来求解。

这些方法在实际应用中具有广泛的用途，不仅可以帮助我们计算距离，还可以应用于问题的建模与解决。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

空间直角坐标系空间两点间的距离公式班级：____________ 姓名：__________________
C ．(－4,0，－6)
D ．(－4,7,0)
解析：点M 关于y 轴对称的点是M ′(－4,7，－6)，点M ′在xOz 平面上的射影的坐标为(－4,0，－
6)．
答案：C
二、填空题
7．如图，长方体ABCD －A 1B 1C 1D 1中，已知A 1(a,0，c )，C (0，b,0)，则点B 1的坐标为________． 解析：由题中图可知，点B 1的横坐标和竖坐标与点A 1的横坐标和竖坐标相
同，点B 1的纵坐标与点C 的纵坐标相同，所以点B 1的坐标为(a ，b ，c )．
答案：(a ，b ，c )
8．在空间直角坐标系中，点(4，－1,2)关于原点的对称点的坐标是________．
解析：空间直角坐标系中关于原点对称的点的坐标互为相反数，故点(4，－1,2)关于原点的对称点的坐标是(－4,1，－2)．
答案：(－4,1，－2)
9．点P (－1,2,0)与点Q (2，－1,0)的距离为________．
解析：∵P (－1,2,0)，Q (2，－1,0)，
∴|PQ |＝(－1－2)2＋[2－(－1)]2＋02＝3 2.
答案：3 2
10．已知点P ⎝⎛⎭⎫32，52，z 到线段AB 中点的距离为3，其中A (3,5，－7)，B (－2,4,3)，则z ＝________.
解析：由中点坐标公式，得线段AB 中点的坐标为⎝⎛⎭
⎫12，92，－2.又点P 到线段AB 中点的距离为3，所以
⎝⎛⎭⎫32－122＋⎝⎛⎭
⎫52－922＋[z －(－2)]2＝3， 解得z ＝0或z ＝－4.
答案：0或－4
三、解答题
11．已知直三棱柱ABC －A 1B 1C 1中，∠BAC ＝90°，|AB |＝|AC |＝|AA 1|＝4，M 为BC 1的中点，N 为A 1B 1的中点，求|MN |.
解析：如右图，以A 为原点，射线AB ，AC ，AA 1分别为x 轴，y 轴，z 轴的正半轴建立空间直角坐标系，
则B (4,0,0)，C 1(0,4,4)，A 1(0,0,4)，B 1(4,0,4)，因为M 为BC 1的中点，N 为A 1B 1的中点，所以由空间
直角坐标系的中点坐标公式得M (4＋02，0＋42，0＋42)，N (0＋42，0＋02，4＋42
)，即M (2,2,2)，N (2,0,4)． 所以由两点间的距离公式得
|MN |＝(2－2)2＋(2－0)2＋(2－4)2＝2 2.
12．已知点P (2,3，－1)，求：
(1)点P 关于各坐标平面对称的点的坐标；
(2)点P 关于各坐标轴对称的点的坐标；
(3)点P 关于坐标原点对称的点的坐标．
解析：(1)设点P 关于xOy 坐标平面的对称点为P ′，则点P ′的横坐标、纵坐标与点P 的横坐标、纵坐标相同，点P ′的竖坐标与点P 的竖坐标互为相反数．
所以点P 关于xOy 坐标平面的对称点P ′的坐标为(2,3,1)．同理，点P 关于yOz ，xOz 坐标平面的对称点的坐标分别为(－2,3，－1)，(2，－3，－1)．
(2)设点P 关于x 轴的对称点为Q ，则点Q 的横坐标与点P 的横坐标相同，点Q 的纵坐标、竖坐标与点P 的纵坐标、竖坐标互为相反数．
所以点P 关于x 轴的对称点Q 的坐标为(2，－3,1)．
同理，点P 关于y 轴，z 轴的对称点的坐标分别为(－2,3,1)，(－2，－3，－1)．
(3)点P (2,3，－1)关于坐标原点对称的点的坐标为(－2，－3,1)．
13．如图，已知长方体ABCD －A 1B 1C 1D 1的对称中心在坐标原点，交于同一顶点的三个面分别平行于三个坐标平面，顶点A (－2，－3，－1)，求其他七个顶点的坐标．
解析：由题意，得点B 与点A 关于xOz 平面对称，
故点B 的坐标为(－2,3，－1)；
点D 与点A 关于yOz 平面对称，故点D 的坐标为(2，－3，－1)；
点C 与点A 关于z 轴对称，故点C 的坐标为(2,3，－1)；
由于点A 1，B 1，C 1，D 1分别与点A ，B ，C ，D 关于xOy 平面对称，
故点A 1，B 1，C 1，D 1的坐标分别为A 1(－2，－3,1)，B 1(－2,3,1)，C 1(2,3,1)，D 1(2，－3,1)．
14．已知点M (3,2,1)，N (1,0,5)，求：
(1)线段MN 的长度；
(2)到M ，N 两点的距离相等的点P (x ，y ，z )的坐标满足的条件．
解析：(1)根据空间两点间的距离公式得
|MN |＝(3－1)2＋(2－0)2＋(1－5)2＝26，
所以线段MN 的长度为2 6.
(2)因为点P (x ，y ，z )到M ，N 两点的距离相等，所以
(x －3)2＋(y －2)2＋(z －1)2＝(x －1)2＋(y －0)2＋(z －5)2，
化简得x ＋y －2z ＋3＝0，
因此，到M ，N 两点的距离相等的点P (x ，y ，z )的坐标满足的条件是x ＋y －2z ＋3＝0.。