空间两点之间的距离公式

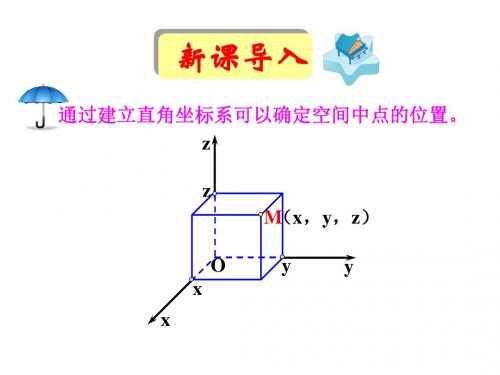
两点间距离公式用法
两点间距离公式用法：
两点间距离公式是用来计算平面上或空间中两个点之间距离的公式。

在平面上，我们可以使用勾股定理来计算两点间的距离，而在三维空间中，我们需要使用三维勾股定理来计算。

在平面上，如果给定两个点的坐标为 (x1, y1)和 (x2, y2)，那么可以使用勾股定
理来计算它们之间的距离。

勾股定理的公式为：d = √((x2 - x1)² + (y2 - y1)²)，其中
d 表示两点之间的距离。

在三维空间中，如果给定两个点的坐标为 (x1, y1, z1)和 (x2, y2, z2)，我们可以
使用三维勾股定理来计算它们之间的距离。

三维勾股定理的公式为：d = √((x2 -
x1)² + (y2 - y1)² + (z2 - z1)²)，其中 d 表示两点之间的距离。

使用这些公式时，我们需要将两个点的坐标代入相应的公式中，然后进行计算。

最终得到的结果就是两点之间的距离。

需要注意的是，这些公式只适用于平面上或空间中的直线距离计算。

如果需要
计算两点之间的其他类型的距离，如曲线或曲面上的距离，可能需要使用其他公式或方法进行计算。

总而言之，两点间距离公式是用来计算平面上或空间中两个点之间距离的数学
工具。

通过代入坐标并使用相应的公式，我们可以准确计算出这两点之间的距离。

空间直角坐标系点面距离公式(一)空间直角坐标系点面距离公式一、点到点的距离公式两点之间的距离可以用勾股定理来计算，即两点间直线的欧氏距离公式。

公式如下：d = √[(x2 - x1)² + (y2 - y1)² + (z2 - z1)²]其中，(x1, y1, z1)、(x2, y2, z2) 分别为两个点的坐标。

示例：假设有两个点 A(1, 2, 3) 和 B(4, 5, 6)，要计算它们之间的距离。

根据公式计算可得：d = √[(4 - 1)² + (5 - 2)² + (6 - 3)²]= √[3² + 3² + 3²]= √[9 + 9 + 9]= √27≈所以点 A 到点 B 的距离约为。

二、点到直线的距离公式点到直线的距离可以利用点到点的距离公式来计算。

设点 P(x, y, z) 到直线 L 的距离为 d，直线 L 上一点为 A(x1, y1, z1)，则有：d = |(Ax - Px) * i + (Ay - Py) * j + (Az - Pz) * k|/ √(i² + j² + k²)其中，(x, y, z) 为点 P 的坐标，(x1, y1, z1) 为直线上一点的坐标，(i, j, k) 为直线的方向向量。

示例：考虑一条直线 L 过点 A(1, 2, 3)，且方向向量为 (2, 2, 1)。

现有一点 P(-1, 0, 1)，要计算 P 到直线 L 的距离。

根据公式计算可得：d = |(2(-1 - 1) + 2(0 - 2) + 1(1 - 3))| / √(2² + 2²+ 1²)= |-4 - 8 - 2| / √(4 + 4 + 1)= |-14| / √9= 14 / 3≈所以点 P 到直线 L 的距离约为。

三、点到平面的距离公式点到平面的距离可以类比点到直线的距离公式，利用点到点的距离公式来计算。

两点之间的距离计算公式在数学中，两点之间的距离可以通过使用坐标系的方法来计算。

坐标系是一个图形化的方法，用于定位和测量点之间的距离。

假设我们有两个点A和B，它们分别具有(x1,y1)和(x2,y2)的坐标。

我们可以使用直角三角形的定理来计算两个点之间的距离。

直角三角形的定理是基于勾股定理。

根据这个定理，两个直角三角形的直角边的平方和等于斜边的平方。

在我们的例子中，斜边就是点A到点B的距离，而直角边就是每个点的x坐标和y坐标之间的差值。

因此，两点之间的距离d可以用以下公式计算：d=√[(x2-x1)²+(y2-y1)²]这个公式适用于任何两个二维坐标系中的点。

让我们通过一个简单的例子来解释：假设我们有两个点A(2,3)和B(5,7)。

我们可以使用上述公式计算它们之间的距离。

首先，我们计算x坐标之间的差值：5-2=3然后，我们计算y坐标之间的差值：7-3=4接下来，我们将这些差值的平方相加：3²+4²=9+16=25最后，我们将这个和开根号所以，点A和点B之间的距离为5个单位。

这个公式也可以扩展到三维坐标系中。

在三维中，我们有三个坐标轴（x，y，z），因此两个点之间的距离公式变为：d=√[(x2-x1)²+(y2-y1)²+(z2-z1)²]这个公式适用于在空间中计算两个点之间的距离。

总结：两点之间的距离可以通过使用直角三角形的定理来计算，在二维坐标系中使用d=√[(x2-x1)²+(y2-y1)²]的公式，在三维坐标系中使用d=√[(x2-x1)²+(y2-y1)²+(z2-z1)²]的公式。

这些公式是计算两点之间的距离的基础。

通过了解这些公式，我们可以在数学和物理中应用它们，计算点之间的距离。

两点之间的距离计算在几何学中，计算两点之间的距离是一项基本任务。

无论是在数学领域还是在实际应用中，我们经常需要计算两个点之间的距离。

本文将介绍几种常见的方法和公式，帮助读者准确计算两点之间的距离。

方法一：直线距离公式最常用的计算两点之间距离的方法是直线距离公式，也被称为欧几里得距离公式。

这个公式基于平面上的直角三角形的勾股定理，可以应用于二维和三维空间。

对于平面上的两点A（x1，y1）和B（x2，y2），直线距离公式可以表示为：d = √((x2 - x1)^2 + (y2 - y1)^2)其中，d表示两点之间的距离。

例如，假设点A坐标为（2，3），点B坐标为（5，7），我们可以使用直线距离公式计算两点之间的距离：d = √((5 - 2)^2 + (7 - 3)^2)= √(3^2 + 4^2)= √(9 + 16)= √25= 5因此，点A和点B之间的距离为5个单位。

方法二：曼哈顿距离公式曼哈顿距离是另一种常见的计算两点之间距离的方法。

该方法基于在平面上的直角路径，而不是直线路径。

曼哈顿距离常用于城市规划和计算机图形学等领域。

对于平面上的两点A（x1，y1）和B（x2，y2），曼哈顿距离公式可以表示为：d = |x2 - x1| + |y2 - y1|例如，假设点A坐标为（2，3），点B坐标为（5，7），我们可以使用曼哈顿距离公式计算两点之间的距离：d = |5 - 2| + |7 - 3|= 3 + 4= 7因此，点A和点B之间的曼哈顿距离为7个单位。

方法三：球面距离公式当我们需要在三维空间或地理球面上计算两点之间的距离时，直线距离公式和曼哈顿距离公式都不再适用。

此时，我们可以使用球面距离公式来计算。

球面距离公式基于球面三角形的余弦定理，可以应用于球体上的两点。

对于球面上的两点A（lat1，lon1）和B（lat2，lon2），球面距离公式可以表示为：d = R * arccos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 -lon1))其中，d表示两点之间的距离，R表示球体的半径。

两点之间的距离公式在数学中，两点之间的距离是指在数学空间中测量两个点之间的长度。

这个概念在几何学、代数学和物理学等多个领域中都有广泛的应用。

在平面几何中，两个点之间的距离可以使用勾股定理来计算。

勾股定理指的是一个直角三角形的两条直角边的平方和等于斜边的平方。

这个定理可以用来计算两点之间的距离，其中斜边即为两点之间的距离。

假设有两个点A（x1,y1）和B（x2,y2），我们可以通过勾股定理来计算它们之间的距离。

根据定理，我们可以将两点之间的距离表示为：d=√((x2-x1)^2+(y2-y1)^2)其中，d表示点A和点B之间的距离。

这个公式的推导过程是通过勾股定理来进行的。

根据勾股定理，直角三角形的斜边的平方等于直角边的平方之和。

在这个情况下，直角边对应（x2-x1）和（y2-y1），斜边对应d。

将这些值代入勾股定理的公式中，我们可以得到两点之间的距离公式。

这个距离公式可以扩展到三维空间，其中点A（x1,y1,z1）和点B（x2,y2,z2）之间的距离可以表示为：d=√((x2-x1)^2+(y2-y1)^2+(z2-z1)^2)这个公式的推导过程与二维情况类似，只是在三维空间中需要考虑三个坐标轴。

除了直角坐标系外，两点之间的距离公式还可以根据其他坐标系进行推导。

例如，在极坐标系中，可以使用极坐标变换公式将两点的极坐标表示转换为直角坐标表示，然后使用上述的距离公式进行计算。

另外，两点之间的距离公式还可以应用于更高维度的空间。

例如，在四维空间中，两点A（x1,y1,z1,w1）和B（x2,y2,z2,w2）之间的距离可以表示为：d=√((x2-x1)^2+(y2-y1)^2+(z2-z1)^2+(w2-w1)^2)这个公式的推导过程与二维和三维情况相似，只是需要考虑四个坐标轴。

综上所述，两点之间的距离公式可以通过勾股定理推导得出，并可以适用于平面几何和空间几何中的不同坐标系。

这个公式在数学和物理学中有广泛的应用，例如在测量、导航和机器学习等领域中。