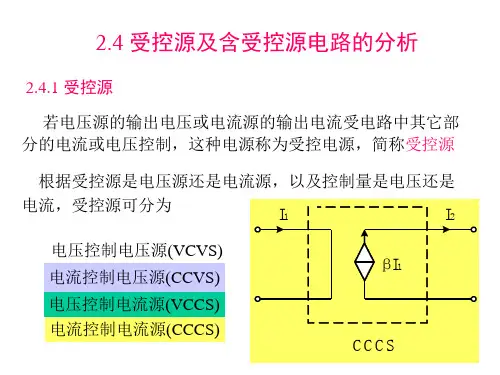
最新2.4 受控源及其等效变换
- 格式:ppt
- 大小:369.50 KB
- 文档页数:6

关于受控电源的简要分析摘要:利用等效变换把受控源支路等效为电阻或电阻与独立电压源串联组合求解含有受控源的现行电路。
关键词:受控电源;等效变换;独立电源前言:在求解含有受控源的线性电路中,存在着专门大的局限性.下面就此问题作进一步的探讨.受控源支路的电压或电流受其他支路电压、电流的操纵.受控源又间接地阻碍着电路中的响应.因此,不同支路的网络变量间除拓扑关系外,又增加了新的约束关系,从而使分析计算复杂化.如何揭露受控源隐藏的电路性质,这对简化受控源的计算是超级重要的.本文在对受控源的电路性质进行系统分析的基础上,给出了含受控源的线性电路的等效计算方式.正文:概述:在电路基础课程中,对含受控源的线性电路分析一直以来都是一个难点。
究其原由,是因为受控源具有与独立源完全不同的特性,它描述电路中两条支路电压或电流间的约束关系。
它的存在通常与两个量有关,一个是独立电源,另一个是受控源的操纵量,其中独立源是全然,没有独立源也就没有操纵量和受控源。
一样电路理论文献以为:独立源产生操纵量,控制量作用于受控源,受控源不能离开操纵量而存在,操纵量变,受控源也变。
在运用节点法、回路法和受控源的等效变换方面,可将受控源看成独立源处置;而一旦运用到叠加定理及求含受控源电路的戴维南等效电阻时,受控源却不能像独立源一样处置了。
如在叠加定理应用中,指出在每一个分电路中受控源要和电阻一样始终保留在电路中,即是将受控源看成电阻处理。
因此,受控源老是担负着一种既不是独立源又不是纯电阻的为难角色,具有双重性,从而使含受控源的电路分析计算难度加深。
其实,受控源的这一双重性是辨证统一的,若是在处置含受控源电路时,或将受控源视为“独立源”,或将受控源视为“电阻”,将使电路分析计算大大简化。
依照受控源的操纵量所在支路的位置不同,别离采取如下3种等效变换法.1. 1.当电流操纵型的受控电压源的操纵电流确实是该受控电压源支路的电流、或当电压操纵型的受控电流源的操纵电压确实是该受控电流源支路两头的电压时,该受控源的端电压与电流之间就成线性比例关系,其比值确实是该受控源的操纵系数.因此,可采纳置换定理,将受控源置换为一电阻,再进一步等效化简.例1-1:如图求解图a中所示电路的入端电阻R AB.解:第一,将电压操纵型的受控电流源gu1与R1并联的诺顿支路等效转变成电压操纵型的受控电压源gu1R1与电阻R1串联的等效戴维南支路,如图b所示.在电阻R1与电阻R2串联化简之前,应将受控电压源的操纵电压转换为端口电流i,即u 1=-R2i.然后,将由电压u1操纵的电压操纵型受控电压源gu1R1转化为电流操纵型的受控电压源-gR1R2i,如图c所示.由图c可知,由于该电流操纵型的受控电压源的操纵电流i确实是该受控电压源支路的电流,因此,可最终将该电流操纵型的受控电压源简化成一个电阻,其阻值为-gR1R2.如此,该一端口网络的入端电阻R AB=R1+R2-gR1R2.-Ba+例1—2 例1—2 求解图a 中所示电路的入端电阻R AB .解:可对该一端口网络持续运用戴维南-诺顿等效变换,最后可取得图 b 所示的电路.由于电压操纵型的受控电流源u1 8Ω的操纵量u1确实是它的端电压,且二者的假定正方向相反,因此,可将其简化为一阻值为-8Ω的电阻.如此,该一端口网络的入端电阻R AB =1/(1 2+1 2-1 8)=8 72. 2. 受控源的操纵量为网络的端口电压或电流时,可将各支路进行等效变换,可将受控源作为独立源处置.当电路等效到端口时,假设操纵量是端口电流,那么可将电路等效成受控电压源、独立电压源和电阻的串联组合;假设操纵量是端口电压,那么可将电路等效成受控电流源、独立电流源和电阻的并联组合.再进一步将受控源置换为一电阻,最后可求出最简单的等效电路. 例2—1 例2—1 简化图a 所示电路.-Ba+_BR 2R 1ib++-Bc111a 1111aU18b解:先将图4a 的受控电流源化为等效的受控电压源,归并后取得图4b 所示电路.将图4b 的受控电压源化为等效的受控电流源,再归并后取得图4c .因操纵量是端口电流,将电路等效成受控电压源和电阻的串联组合,取得图4d .最后,将受控源置换为一电阻-8Ω(如前所述),那么:R AB =-8+4 5= -36 5(Ω)由此可知,图 a 所示的一端口网络对外电路而言,相当于RAB =-36/5Ω的一只负电阻.3. 3. 受控源的操纵量支路为网络中任意其他支路时,在含受控源的线性电路中,为了维持受控源两条支路之间的耦合关系不变,在求解电路时一样要保留操纵量所在的支路,这对电路的分析计算带来许多限制,为此,咱们提出将受控源等效置换成独立电源的形式,使其不受电路结构的限制. 在一个网络中操纵量与网络变量之间的关系是由电路结构确信的,并被基尔霍夫定律互连约束和欧姆定律元件约束于电路中. 在分析电路时,能够将原操纵量变换为另一个新的操纵量而可不能改变电路的状态,即可用受控电压源的电流或受控电流源的端电压作为受控源新的操纵量.新操纵量与原操纵量之间为线性关系,它是由基尔霍夫定律和欧姆定律确信的.对电压操纵型受控电压源VCVS 可等效为u 2=μu 1=μ(m 1+n 1i )=μm 1+μn 1i对电压操纵型受控电压源CCVS 可等效为u 2=ri 1=r (m 2+n 2i )=rm 2+rn 2i对电压操纵型受控电压源VCCS 可等效为i 2=gu 1=g (m 3+n 3u )=gm 3+gn 3u对电压操纵型受控电压源CCCS 可等效为a aaaabcRabi 2=βi 1=β(m 4+n 4u )=βm 4+βn 4u式中:i,u ——受控电压源的电流和受控电流源的电压,即为受控源新的控m 1,m 2,m 3,m 4——常数,表示独立源的等效作用;n 1,n 2,n 3,n 4——常数,表示两支路响应间的转移系数. 由上式得出如图受控源的等效变换形式.从图中可见,受控电压源可用一独立电压源(其电压等于μm 1或rm 2)与一个电阻(其阻值等于μn 1或rn 2)的串联组合支路来等效,受控电流源可用一独立电流源(其电流等于gm 3或βm 4)与一个电导(其电导等于gn 3或βn 4)的并联组合支路来等效.其等效电路中的电源数值为原网络中独立电源的线性组合,而电阻参数与原网络中其他某些元件参数相关.从上述分析可知:受控源的电源与独立源的电源有所不同,独立源的电源是电路中的鼓励,有了它才能在电路中产生电流和电压;而受控源的电源那么不同,它的电压或电流受其他电压或电流的操纵,并最终受控于独立源,当独立源为零时,受控源也失去了电源的作用.例3—1见图a所示电路中虚线框出的电路部份可否用戴维南定理来化简?-+u 2i VCVSau 2CCVSb+-u VCCScu CCCSd解:显然,要保留受控源两条支路之间的耦合关系,有虚线框的部份是无法用戴维南定理简化的,但假设对受控源等效变换后,那么能够简化.现分析如下(电流单位为mA ).将受控电流源与R3=6k Ω的电阻并联等效为受控电压源与R3的串联组合,如图b 所示.b 式中,U k =2×103U 1×6×10-3=12U 1=12I 1R 1=12I 1×10-3×2×103=24I 1(V)列出节点a 电流方程I k +I s =I 1,即I 1=6+I k (mA),那么U k =24I 1=24(6+I k )=144+24I k (V)因此,受控源的受控支路可用U S =144V 的电压源与R k =24k Ω的电阻串联来等效代替,见图c .该电路虚线框图中的电路可用戴维南定理来简化,其等效电路如图d 虚线框图所示,Us ’=Us-E=144-12=132 R i =R k +R 3=24+6=30(k Ω)acd通过计算,变换前后外电路各支路电流、电压(I 1均为2.1mA ,Uab ,均为4.2V ),可验证等效变换的正确性.小结:由以上分析可知,受控源能够用等效的独立电源或一个阻抗置换,且不阻碍等效部份对外电路的阻碍。