受控电源的等效方法

含受控源二端网络等效电阻的求解作者：黄艳来源：《科技资讯》2014年第35期摘要：受控源电路是电路分析中常见的电路，在“电路分析”课程教学中，戴维宁定理、最大功率传输定理以及动态电路时间常数的分析和计算时都需要进行等效电阻的求解，因而其中含受控源二端网络输入电阻的求解与分析既是重点也是难点。

该文利用受控源的双重特性讨论了含受控源二端网络输入电阻的三种求解方法：外加电源法、开路电压短路电流法、电阻等效变换法，对每种方法的应用进行了举例，并通过举例进行了分析，给出了应用时的注意事项，实践证明这样更方便于学生在学习时能够系统地掌握含受控源二端网络等效电阻的求解。

关键词：受控源等效电阻外加电源法开路电压短路电流法电阻等效变换法中图分类号：TM13 文献标识码：A 文章编号：1672-3791（2014）12（b）-0179-02受控源电路是电路分析中非常重要的一部分，不管是叠加定理、戴维宁定理、网孔电流分析法、节点电压分析法等，都会遇到含受控源的电路，而且在电子技术不断发展的今天，受控源电路也出现的越来越多，其重要性也不言而喻。

但学生在学习含受控源电路的分析方法时，普遍反映该部分知识较难掌握。

在“电路分析”课程教学中，戴维宁定理、最大功率传输定理以及动态电路时间常数的分析和计算时都需要进行等效电阻的求解，因此，含受控源二端网络等效电阻的求解在电路学习过程中具有举足轻重的地位。

该文利用受控源的双重特性对含受控源二端网络等效电阻的求解方法进行了总结，以便学生在学习过程中更容易理解。

1 受控源电源分为独立电源和非独立电源。

独立电源是指能够产生电压和电流的电源，电压值或电流值由其本身决定，不受外界控制。

而非独立电源的参数受控制支路的电流或电压的控制，因此非独立源又叫受控源。

控制量可以是电压也可以是电流，根据控制量的不同可以分为电压控制的电压源（VCVS）、电流控制的电压源（CCVS）、电压控制的电流源（VCCS）、电流控制的电流源（CCCS）。

含受控源电路等效化简时控制量支路的一种处理方法冯向莉:含受控坚蔓鳖量塞坚=堡直含受控源电路等效化简时控制量支路的一种处理方法冯向莉(陕西理工学院电工电子实验中心陕西汉中723003)摘要:在电路的等效变换中,当电路中含受控电源时,电路的化简往往是一个难点,通常的做法是保留控制量支路.本文介绍一种不用保留控制量支路的处理方法,可在处理某些类似问题时显得更简便,灵活.文中给出了算例以及用该方法求解电路的过程.关键词:受控源;控制量支路;等效变换;处理方法中图分类号:TN702文献标识码:B文章编号:1004—373X(2005)1l一116一O2 ANewMethodonControlBranchesintheCircuitsofContainingControlled SourcewhenDealingwithEquivalentEffectiveSimplificationFENGXiangli(ElectricalandElectronicExperimentCenter.ShaaxnxiUniversityofTechnology.Hanzhon g,723003.China)Abstract:Inthecircuitequivalentconverter,whenelectroniccircuitscontainthecontrolledso urce,itSusuallydifficulttosimplifytheelectroniccircuits.Theusualmethodistokeepthecontrolvariablebranches.Thispaperint roducesanewmethodthatthecontrolvariablebranchesarenotkept.Thismethodcanmakesomeproblemsbecomeeasyandflexibl etosolve.Thispapergivessome calculationandtheprocessofcollectingcircuitswiththismethod.Keywords:controlledsource;controlledvariablebranches;equivalentconverter;method 1问题的提出及处理方法在含有电源的电路中,电源有2类:一类是独立电源,是一个单口理想元件,他是电路的激励,表征外界对电路的作用;另一类是非独立源(受控源),是一个双口理想元件,常用来模拟电子元器件(比如晶体管)的特性等,表征两条支路间网络变量的耦合关系.一般认为,为了保持两条支路间的耦合关系不变,在对电路等效化简时,通常不要把控制量所在的支路变换掉,否则控制量将随控制支路一道被消掉而无法计算出结果.笔者认为,在等效化简过程中,即使把控制量消去也无妨.因为控制量与网络变量间的关系已随电路结构的确定而被基尔霍夫定理约束于电路之中,而对局部网络的等效化简只相当于将KCL 和KVL中某些变量合并成另一个新变量而已,并不会改变其他支路状态.因此,从表面看控制量似乎已不存在,但实质上他却始终隐含于电路各变量之中.例如对图1(a)所示电路,若将15S电导和3Os电导合并成一个45s的电导其等效电路如图1(b)所示.显然控制量支路已被消去. (a)原电路圈(b)化简电路阔图1举例电路图收祷日期:2004—12—18116但此时45s支路电流可表示为:'nI一I—II一一J一I一一3I』J可见控制量仍然隐含在电路中,只相当于有一条支路通过而已.问题是随着电路结构的每一步变化必须及时找出控制量在等效电路中的代换关系.然而,若在等效变化的过程中先不计及控制量的代换关系,虽然在化简所得的最后电路中已看不到控制量与网络变量间的关系,然而总可在原电路中找出控制量与最终等效电路中某网络变量间的代换关系,从而解得所需要的结果.2举例说明例1试求图2(a)所示电路中的.岛囱(a)原电路图Co)化简电路幽(c)化简电路图图2例1的电路图解法一:用通常的方法,即保留控制量支路进行计算.将图2(a)中控制量支路以外的电路化简后的等效电路如图2(b).由图列出KCL方程:,,A21++一÷一01?J0由欧姆定律得:U一0.5I,代人上式可得I,一0.4A.解法二:用不保留控制量支路方法进行计算.将2005年第1期总噩星Q星图2(a)中所有电流源模型等效为电压源模型,使之成为单网孔电路,控制量支路被消去,如图2(c)所示.由图可得: I=(2+I)/(1.5+0.5)=1+0.5I.由原电路可找出控制量的代换关系为:I—I+2I一3I从而解得:I=0.4A.两种解法的结果相同.本例题中,显然无论从电路等效过程还是最后的电路计算,后一种解法更显简便.例2试求图3(a)电路中的U.【h)化简电路图图3例2的电路图解:本例中可先求再求U=6×(9一).将原电路图3(a)中支路两边电路分别等效成电压源模型.其等效电路如图3(b)所示,显然控制量.已被消隐.由图3(b)列出KVL方程:(6+2)+3.一88—0由图3(b)得控制量的代换关系式:I=2I+17.从而解得:全11.94A.所以:U,=6×(9一)==:一17.64V.例3试求图4(a)电路中的.和..解:将原电路图4(a)逐步等效变换为图4(c).由图列出KVL方程:8.1J.+18一18—0由原电路可得:I=一I.+1+[(36—18I.)/36]一(18I./36)一2—2.或可由简化过程中的一个中间等效电路图4(b)求得:I=2—2.代人KVL方程解得:.全0.645mA;U.=18I.全11.61V.3结语【b)化简电路图(c)化简电路图图4例3原电路图及化简电路(1)对含受控源电路进行等效化简时,可以不保留控制量支路,只要在原电路(或在化简过程中的某一中间电路)中列出控制量与某网络变量间的代换关系即可解得最后的结果.(2)对于某些类型的电路,较易从原电路中找出控制量与网络变量的代换关系,化去控制量支路往往会使等效变换更加灵活或使等效电路变得更简单便于计算.因此,这种方法也是一种有效的处理方法.参考文献[1]邱关源.电路[M].第3版.北京:高等教育出版社,1990.[2]张宇飞.关于含受控源电路分析的新方法[J].陕西工学院,2000,16(1):22—26.[3]冯向莉.含受控源电路中控制量变换的探讨[J].陕西工学院,2000,16(2):17—2O(上接第115页)传输一个完整8位数据时,先传送数据的最高位(MSB).在前一个8位数据传送完后,PC7会变为高电平,为了启动下一个8位数据的写操作,PC7引脚必须被置为低电平.4结语AD5621采用SC70封装,接口简单,使用方便,灵活,便于精密输出控制,同时又具备很低的功耗.该芯片具有很强的实用性,能够满足当前系统对低功耗,小封装和低成本的要求,从而为大批量应用提供优秀的解决方案.参考文献[1]AnalogDevicesInstruments.nanoDACD/A,SPIInterface,SC70Package,2004.[2]Motorola.M68HC11ReferenceManua1.2001.[3]刘书明.高性能模/数与数/模转换器件[M].西安:西安电子科技大学出版社,2000.[4][美]TocciRJ,AmbrosioFJ.微处理器与微型计算机:硬件和软件[M].第6版.李小洪,冯昭群译.北京:清华大学出版社,2004.作者简介冯波男,1977年出生,湖南益阳人,学士,武警湖南总队助理工程师.金童4男,1978年出生,江西临;I1人,硕士,教师.主要研究方向为数字通信网,数字图像处理,DSP及可骗程逻辑器件. 117。

含受控源戴维南等效电路求解步骤嘿，朋友们！今天咱就来唠唠含受控源戴维南等效电路求解步骤这个事儿。

咱先得明白，这受控源啊，就像是电路里的一个“小调皮”，你得好好捉摸它的脾气。

那求解第一步呢，就是把要求解的那部分电路从整个电路里“揪”出来，就像从一堆杂物里找出你想要的宝贝一样。

然后呢，把那些独立源都关掉，就当它们去“睡觉”啦！这时候再看看受控源，嘿，它可还在那呢。

接下来就要计算这部分电路的开路电压啦，这就好比给这部分电路量量“身高”。

计算开路电压的时候，可不能马虎哦，得仔细分析那些元件之间的关系，就像解开一团乱麻一样，要有耐心。

等算出开路电压了，咱就进入下一步啦，就是把电路里的独立源都去掉，只留下受控源和电阻啥的。

这就好像把舞台上的无关人员都请下去，只留下主角和配角。

接着呢，计算等效电阻。

这可有点像给电路称称“体重”，看看它到底有多重。

计算等效电阻的时候，可能会用到一些巧妙的方法，比如外加电源法之类的。

哎呀，这一步步的，不就跟咱盖房子似的嘛，得先打地基，再一层层往上盖。

等把开路电压和等效电阻都搞定了，那最后一步，就像给房子安上
一个漂亮的屋顶一样，把它们组合起来，就得到了含受控源戴维南等
效电路啦！
你说这神奇不神奇？咱通过这一系列的操作，就能把一个复杂的含
受控源电路变得简单易懂。

就好像把一本厚厚的书，精简成了一个薄
薄的小册子。

总之啊，求解含受控源戴维南等效电路可不能着急，得一步一步慢
慢来，就像走在一条小路上，得稳稳当当的。

只要咱有耐心，有细心，还怕搞不定它吗？咱肯定能行的呀！所以，大家都鼓起劲儿来，去试
试吧！。

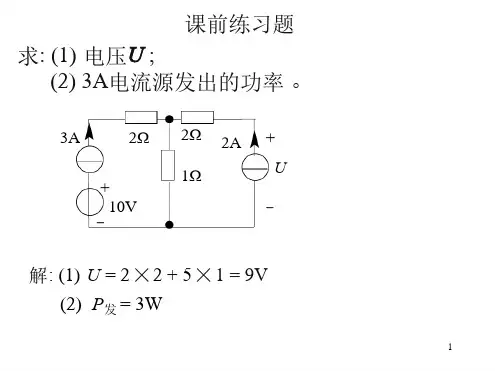
受控电流源等效电阻
受控电流源是一种电子元件，它可以提供一个稳定的电流输出。

然而，实际使用中，受控电流源会产生一定的内部电阻。

这个内部电阻会对电路产生影响，在某些情况下需要将其等效成一个电阻。

等效电阻是指在相同条件下，具有相同电流和电压的电阻所产生的功率和效果与实际电路中存在的内部电阻相同。

因此，将受控电流源等效成一个电阻可以更好地分析和设计电路。

通常，受控电流源的内部电阻可以通过 Ohm 定律来计算。

如果电源的输出电流是 I，而它的内部电阻是 R，那么它的内部电阻可以表示为 V=IR，其中 V 是电源的输出电压。

在一些应用中，需要将受控电流源等效成一个电阻。

为了实现这一点，可以使用串联电阻来模拟受控电流源的内部电阻。

这个串联电阻的值应该等于受控电流源的内部电阻。

这样，电路中的电流和电压就可以在等效电阻和串联电阻之间进行计算。

在设计电路时，受控电流源的等效电阻是一个非常重要的参数。

因为等效电阻可以影响电路的功率和稳定性，所以需要认真计算和考虑。

通过使用适当的电路设计工具和方法，可以更好地控制电路中的等效电阻，并实现更好的电路性能和效果。

- 1 -。

线性电路分析中受控电源的一种等效方法
李月玲;袁文杰
【期刊名称】《东北电力大学学报》
【年(卷),期】2002(022)002
【摘要】利用等效变换把受控源支路等效为电阻或电阻与独立电压源串联组合来求解含有受控源的现行电路.
【总页数】3页(P77-79)
【作者】李月玲;袁文杰
【作者单位】东北电力学院,轻工系,吉林,吉林,132012;东北电力学院,轻工系,吉林,吉林,132012
【正文语种】中文
【中图分类】TM131
【相关文献】
1.含受控源电路分析的一种改进方法 [J], 田艳芳;杨勇波
2.等效变换在含有受控源线性电路分析中的应用 [J], 李月玲;卢莉
3.在叠加定理中处理线性受控源的一种新方法 [J], 邵思飞;景向伟
4.电路分析中对受控电源的处理原则 [J], 王康兴;
5.含受控源的线性电路分析计算方法研究 [J], 曾小平
因版权原因，仅展示原文概要，查看原文内容请购买。

关于受控电源的简要分析摘要：利用等效变换把受控源支路等效为电阻或电阻与独立电压源串联组合求解含有受控源的现行电路。

关键词：受控电源；等效变换；独立电源前言：在求解含有受控源的线性电路中，存在着专门大的局限性．下面就此问题作进一步的探讨．受控源支路的电压或电流受其他支路电压、电流的操纵．受控源又间接地阻碍着电路中的响应．因此，不同支路的网络变量间除拓扑关系外，又增加了新的约束关系，从而使分析计算复杂化．如何揭露受控源隐藏的电路性质，这对简化受控源的计算是超级重要的．本文在对受控源的电路性质进行系统分析的基础上，给出了含受控源的线性电路的等效计算方式．正文：概述：在电路基础课程中，对含受控源的线性电路分析一直以来都是一个难点。

究其原由，是因为受控源具有与独立源完全不同的特性，它描述电路中两条支路电压或电流间的约束关系。

它的存在通常与两个量有关，一个是独立电源，另一个是受控源的操纵量，其中独立源是全然，没有独立源也就没有操纵量和受控源。

一样电路理论文献以为:独立源产生操纵量，控制量作用于受控源，受控源不能离开操纵量而存在，操纵量变，受控源也变。

在运用节点法、回路法和受控源的等效变换方面，可将受控源看成独立源处置;而一旦运用到叠加定理及求含受控源电路的戴维南等效电阻时，受控源却不能像独立源一样处置了。

如在叠加定理应用中，指出在每一个分电路中受控源要和电阻一样始终保留在电路中，即是将受控源看成电阻处理。

因此，受控源老是担负着一种既不是独立源又不是纯电阻的为难角色，具有双重性，从而使含受控源的电路分析计算难度加深。

其实，受控源的这一双重性是辨证统一的，若是在处置含受控源电路时，或将受控源视为“独立源”，或将受控源视为“电阻”，将使电路分析计算大大简化。

依照受控源的操纵量所在支路的位置不同，别离采取如下3种等效变换法．1. 1.当电流操纵型的受控电压源的操纵电流确实是该受控电压源支路的电流、或当电压操纵型的受控电流源的操纵电压确实是该受控电流源支路两头的电压时，该受控源的端电压与电流之间就成线性比例关系，其比值确实是该受控源的操纵系数．因此，可采纳置换定理，将受控源置换为一电阻，再进一步等效化简．例1-1：如图求解图a中所示电路的入端电阻R AB．解：第一，将电压操纵型的受控电流源gu1与R1并联的诺顿支路等效转变成电压操纵型的受控电压源gu1R1与电阻R1串联的等效戴维南支路，如图b所示．在电阻R1与电阻R2串联化简之前，应将受控电压源的操纵电压转换为端口电流i，即u 1＝－R2i．然后，将由电压u1操纵的电压操纵型受控电压源gu1R1转化为电流操纵型的受控电压源－gR1R2i，如图c所示．由图c可知，由于该电流操纵型的受控电压源的操纵电流i确实是该受控电压源支路的电流，因此，可最终将该电流操纵型的受控电压源简化成一个电阻，其阻值为－gR1R2．如此，该一端口网络的入端电阻R AB＝R1＋R2－gR1R2．-Ba+例1—2 例1—2 求解图a 中所示电路的入端电阻R AB ．解：可对该一端口网络持续运用戴维南－诺顿等效变换，最后可取得图 b 所示的电路．由于电压操纵型的受控电流源u1 8Ω的操纵量u1确实是它的端电压，且二者的假定正方向相反，因此，可将其简化为一阻值为－8Ω的电阻．如此，该一端口网络的入端电阻R AB =1/(1 2+1 2-1 8)=8 72. 2. 受控源的操纵量为网络的端口电压或电流时，可将各支路进行等效变换，可将受控源作为独立源处置．当电路等效到端口时，假设操纵量是端口电流，那么可将电路等效成受控电压源、独立电压源和电阻的串联组合；假设操纵量是端口电压，那么可将电路等效成受控电流源、独立电流源和电阻的并联组合．再进一步将受控源置换为一电阻，最后可求出最简单的等效电路． 例2—1 例2—1 简化图a 所示电路．-Ba+_BR 2R 1ib++-Bc111a 1111aU18b解：先将图4a 的受控电流源化为等效的受控电压源，归并后取得图4b 所示电路．将图4b 的受控电压源化为等效的受控电流源，再归并后取得图4c ．因操纵量是端口电流，将电路等效成受控电压源和电阻的串联组合，取得图4d ．最后，将受控源置换为一电阻－8Ω（如前所述），那么：R AB =-8+4 5= -36 5（Ω）由此可知，图 a 所示的一端口网络对外电路而言，相当于RAB ＝－36／5Ω的一只负电阻．3. 3. 受控源的操纵量支路为网络中任意其他支路时，在含受控源的线性电路中，为了维持受控源两条支路之间的耦合关系不变，在求解电路时一样要保留操纵量所在的支路，这对电路的分析计算带来许多限制，为此，咱们提出将受控源等效置换成独立电源的形式，使其不受电路结构的限制． 在一个网络中操纵量与网络变量之间的关系是由电路结构确信的，并被基尔霍夫定律互连约束和欧姆定律元件约束于电路中． 在分析电路时，能够将原操纵量变换为另一个新的操纵量而可不能改变电路的状态，即可用受控电压源的电流或受控电流源的端电压作为受控源新的操纵量．新操纵量与原操纵量之间为线性关系，它是由基尔霍夫定律和欧姆定律确信的．对电压操纵型受控电压源VCVS 可等效为u 2=μu 1=μ（m 1+n 1i ）=μm 1+μn 1i对电压操纵型受控电压源CCVS 可等效为u 2=ri 1=r （m 2+n 2i ）=rm 2+rn 2i对电压操纵型受控电压源VCCS 可等效为i 2=gu 1=g （m 3+n 3u ）=gm 3+gn 3u对电压操纵型受控电压源CCCS 可等效为a aaaabcRabi 2=βi 1=β（m 4+n 4u ）=βm 4+βn 4u式中：i,u ——受控电压源的电流和受控电流源的电压，即为受控源新的控m 1，m 2，m 3，m 4——常数，表示独立源的等效作用；n 1，n 2，n 3，n 4——常数，表示两支路响应间的转移系数． 由上式得出如图受控源的等效变换形式．从图中可见，受控电压源可用一独立电压源（其电压等于μm 1或rm 2）与一个电阻（其阻值等于μn 1或rn 2）的串联组合支路来等效，受控电流源可用一独立电流源（其电流等于gm 3或βm 4）与一个电导（其电导等于gn 3或βn 4）的并联组合支路来等效．其等效电路中的电源数值为原网络中独立电源的线性组合，而电阻参数与原网络中其他某些元件参数相关．从上述分析可知：受控源的电源与独立源的电源有所不同，独立源的电源是电路中的鼓励，有了它才能在电路中产生电流和电压；而受控源的电源那么不同，它的电压或电流受其他电压或电流的操纵，并最终受控于独立源，当独立源为零时，受控源也失去了电源的作用．例3—1见图a所示电路中虚线框出的电路部份可否用戴维南定理来化简？-+u 2i VCVSau 2CCVSb+-u VCCScu CCCSd解：显然，要保留受控源两条支路之间的耦合关系，有虚线框的部份是无法用戴维南定理简化的，但假设对受控源等效变换后，那么能够简化．现分析如下（电流单位为mA ）．将受控电流源与R3＝6k Ω的电阻并联等效为受控电压源与R3的串联组合，如图b 所示．b 式中，U k =2×103U 1×6×10-3=12U 1=12I 1R 1=12I 1×10-3×2×103=24I 1(V)列出节点a 电流方程I k +I s =I 1,即I 1=6+I k (mA),那么U k =24I 1=24(6+I k )=144+24I k (V)因此，受控源的受控支路可用U S ＝144V 的电压源与R k ＝24k Ω的电阻串联来等效代替，见图c ．该电路虚线框图中的电路可用戴维南定理来简化，其等效电路如图d 虚线框图所示,Us ’=Us-E=144-12=132 R i =R k +R 3=24+6=30(k Ω)acd通过计算，变换前后外电路各支路电流、电压（I 1均为2．1mA ，Uab ，均为4．2V ），可验证等效变换的正确性．小结：由以上分析可知，受控源能够用等效的独立电源或一个阻抗置换，且不阻碍等效部份对外电路的阻碍。