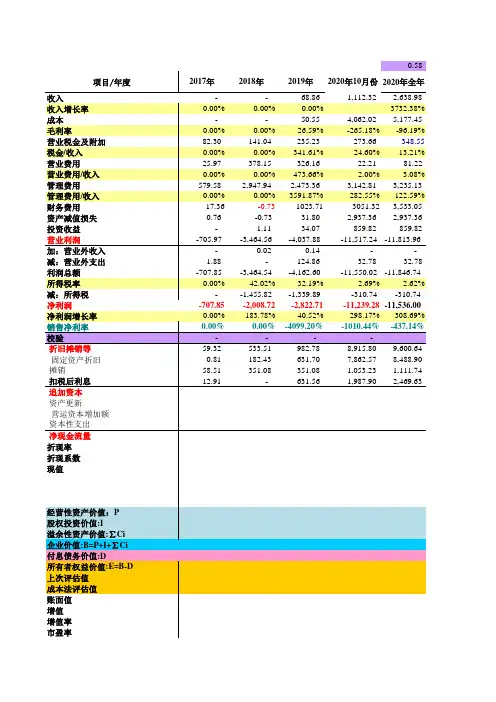
收益法计算表(递增)
- 格式:xls
- 大小:18.00 KB
- 文档页数:1

收益法计算公式范文收益法是一种评估企业价值的方法,它基于企业未来的收益能力来进行计算。
收益法的核心思想是利用企业未来的预期收益,通过贴现的方式将其转化为现在的价值。
收益法的计算公式如下:企业价值=预期未来收益/(1+折现率)^n其中,预期未来收益指的是企业在未来一段时间内所能获得的净利润或者自由现金流,折现率是用来衡量将未来收益转化为现值时所采用的贴现率,n是预期未来收益的时间周期。
在实际应用中,收益法有两种常见的计算方式:净利润法和自由现金流法。
1.净利润法:该方法假定企业在未来一段时间内的净利润呈稳定增长,并以稳定增长的速度持续增加。
计算公式如下:企业价值=(净利润/折现率)*(1-增长率)/(1+折现率)^n其中,增长率指的是净利润的年均增长率。
2.自由现金流法:该方法假定企业在未来一段时间内的自由现金流呈稳定增长,并以稳定增长的速度持续增加。
计算公式如下:企业价值=(自由现金流/折现率)*(1-增长率)/(1+折现率)^n其中,自由现金流是指企业在未来一段时间内扣除了投资支出和运营资本变动后所剩余的可自由支配的现金流量。
还有一些其他的收益法变种,如调整净利润法(考虑资本结构、财务风险等因素)和累计折现现金流法(将多年的自由现金流进行累计和折现)等,但核心思想与上述几种方法基本一致。
需要注意的是,收益法虽然是一种常见的企业估值方法,但其在实际应用中也存在一些限制和假设。
首先,该方法对未来的收益进行了预测和假设,因此对预测准确性要求较高;其次,该方法假设企业未来的收益呈稳定增长,但实际情况中企业的盈利能力可能会受到多种因素的影响,如市场变化、竞争压力等;此外,收益法还需要选择合适的折现率和增长率,这也对估值结果产生一定影响。
总之,收益法是一种重要的企业估值方法,通过将未来的收益贴现以反映其现值,为投资者提供了一个有理论依据的价值评估工具。
然而,在使用时需要综合考虑各种因素,并结合其他估值方法进行综合分析,以提高估值的准确性和可靠性。

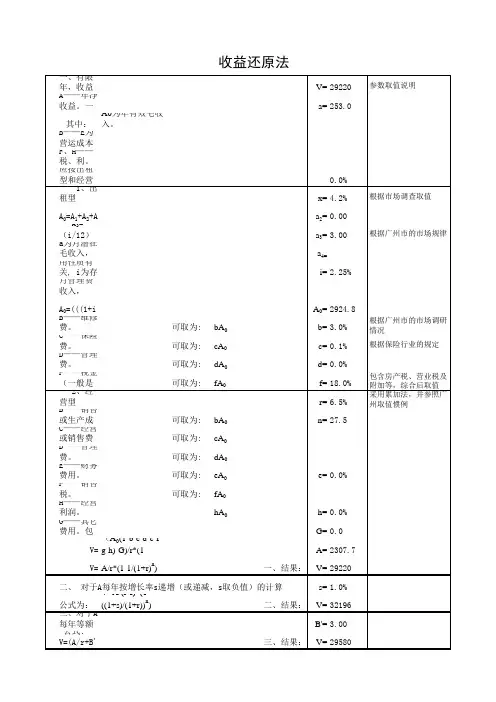
收益法递增公式范文收益法是一种用于估算投资收益的方法,适用于项目期限较长的情况。
递增公式是在收益法的基础上,考虑投资收益逐年递增的情况,能够更为准确地估算项目的收益。
收益法的基本原理是通过估算投资项目的全部未来收入减去支出,得到项目的净现值。
在递增公式中,我们假设投资项目的未来收入会逐年递增。
递增公式的一般形式如下:NPV=Σ(Ct-Ct)/(1+r)^t其中,NPV表示净现值,Ct表示第t年的现金流量,C0表示项目的初始投资,r表示折现率,t表示年数。
接下来,我们将详细介绍递增公式的推导过程,并解释其中的各个参数的含义和用法。
首先,考虑一个投资项目,假设该项目的初始投资为C0,第一年的现金流量为C1,第二年的现金流量为C2,以此类推,第n年的现金流量为Cn。
在递增公式中,我们假设第一年的现金流量为C1,第二年的现金流量为C1*(1+i),第三年的现金流量为C1*(1+i)^2,以此类推,第n年的现金流量为C1*(1+i)^(n-1)。
其中,i表示每年的现金流量递增率。
现在,我们将递增公式代入净现值公式中,得到:NPV=(C1-C0)/(1+r)+(C1*(1+i)-C0)/(1+r)^2+(C1*(1+i)^2-C0)/(1+r)^3+...+(C1*(1+i)^(n-1)-C0)/(1+r)^n化简上述公式,得到:NPV=(C1-C0)/(1+r)+C1*(1+i)/(1+r)^2+C1*(1+i)^2/(1+r)^3+...+C1*(1+i)^(n-1)/(1+r)^n进一步化简,得到:NPV=(C1/(1+r))*(1-(1+i)/(1+r)^n)/(1-(1+i)/(1+r))接下来,我们解释递增公式中的每个参数的含义和使用方法:-NPV:表示投资项目的净现值,即项目的全部未来收入减去支出后的剩余值。
如果净现值大于0,表示项目具有盈利能力;如果净现值小于0,表示项目无盈利能力。
-C1:表示第一年的现金流量,即项目第一年的收入减去支出。

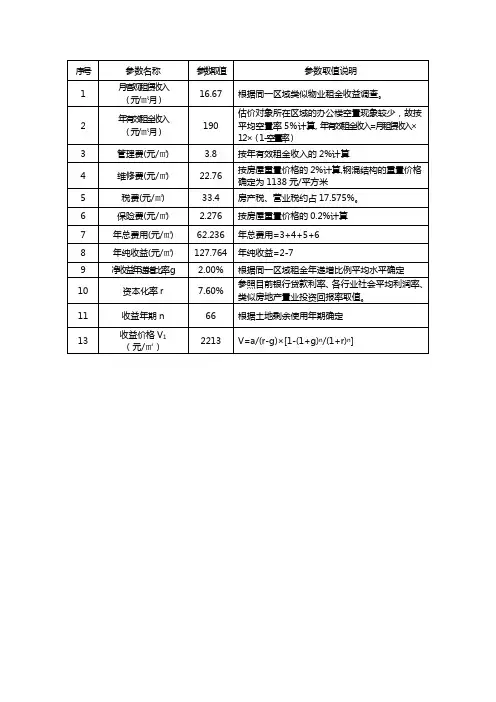
一、等差数列通项公式:求和公式:前n项和公式:二、等比数列通项公式:前n项和公式:三、报酬资本化法最一般的公式四、净收益每年不变的公式【例】某宗房地产是在政府有偿出让的土地上开发建设的,当时获得的土地使用年限为50年,已使用了6年;预计利用该宗房地产正常情况下每年可获得净收益8万元;该宗房地产的报酬率为8.5%。
试计算该宗房地产的收益价格。
【例】已知某宗收益性房地产30年土地使用权、报酬率为10%的价格为3000元/㎡,试求该宗房地产50年土地使用权、报酬率为8%的价格。
五、净收益按一定数额递增的公式【例】预计某宗房地产未来第一年的净收益为25万元,此后每年的净收益会在上一年的基础上减少2万七、净收益按一定比率递增的公式收益期限为48年,该类房地产的报酬率为10%。
试计算该宗房地产的收益价格。
【例】预计某宗房地产未来第一年的净收益为200万元,此后每年的净收益会在上一年的基础上增长2%,收益期限可视为无限年,该类房地产的报酬率为10%。
试计算该宗房地产的收益价格。
八、净收益按一定比率递减的公式【例】预计某宗房地产未来第一年的净收益为240万元,此后每年的净收益会在上一年的基础上递减2%,2、在有效毛收入始终大于运营费用的前提下,收益期限为无限年的计算公式为:【例】预计某宗房地产未来每年的有效毛收入不变,为16万元,运营费用第一年为8万元,此后每年会十、净收益在前后两段变化规律不同的公式【例】某宗房地产的收益期限为38年,通过预测得到其未来5年的净收益分别为20万元、22万元、25万元、28万元、30万元,从未来第6年到第38年每年的净收益将稳定在35万元左右,该类房地产的报酬率为10%。
试计算该宗房地产的收益价格。
【例】通过预测得到某宗房地产未来5年的净收益分别为20万元、22万元、25万元、28万元、30万元,从未来第6年到无穷远每年的净收益将稳定在35万元左右,该类房地产的报酬率为10%。
试计算该宗房地产的收益价格。

收益法等差递增公式好的,以下是为您生成的文章:咱今儿来聊聊收益法等差递增公式,这玩意儿在经济和财务领域里可有着不小的作用呢!先来说说啥是收益法等差递增公式。
简单讲,就是在计算收益的时候,考虑到每年的收益不是一成不变的,而是按照等差数列的方式逐渐增加。
比如说,第一年收益是 A ,每年递增的金额是 B ,那第 n 年的收益就是 A + (n - 1) * B 。
我想起之前有个朋友,开了一家小餐馆。
刚开业那阵子,生意一般般,第一年的净利润也就 5 万块。
但是他特别努力,不断改进菜品,提升服务,生意越来越好。
第二年比第一年多赚了 1 万,第三年又比第二年多赚了 1 万,这就是个典型的等差递增的情况。
那为啥要研究这个等差递增公式呢?其实很好理解。
对于投资者来说,通过这个公式可以更准确地预估未来的收益,从而判断一个项目值不值得投资。
对于企业管理者来说,能帮助他们制定合理的发展策略,知道每年要达到什么样的增长目标。
在实际运用中,可得小心一些细节。
比如说,要准确确定初始收益和递增的金额,这得基于充分的市场调研和实际的经营情况。
要是一开始就估计错了,后面的计算可就全乱套啦。
再比如说,还得考虑到市场的不确定性。
就算前几年收益是等差递增的,也不能保证后面一直这样增长下去。
说不定会遇到竞争对手的冲击,或者行业的大变动。
我还碰到过一个例子,是一家做服装生意的小店。
开始的时候,每年的销售额等差递增,老板可高兴了,准备大干一场。
结果呢,旁边突然开了一家大型商场,抢走了不少客源,递增的趋势就被打破了。
所以啊,虽然收益法等差递增公式能给我们提供一个参考,但不能完全依赖它。
得结合实际情况,灵活运用,不断调整策略,才能在变化多端的市场中站稳脚跟。
总之,收益法等差递增公式是个有用的工具,但用的时候要谨慎,多思考,多观察。
这样才能让它真正为我们的经济决策服务,避免被它给“坑”了。
希望您通过我这一番不太专业但还算实在的讲解,对收益法等差递增公式能有更清楚的认识!。



收益法两阶段公式一、基本原理。
1. 收益法是预计评估对象未来的正常净收益,选用适当的资本化率将其折现到评估基准日并累加,以此估算资产价值的方法。
在很多情况下,企业的发展会呈现出不同的阶段,所以采用两阶段模型来评估企业价值更为合适。
二、两阶段公式。
1. 假设企业在前段时期(通常为高速增长期)按一个较高的增长率g₁增长,持续n年,n年后进入稳定增长期,增长率为g₂。
- 企业整体价值(V)=预测期价值+后续期价值。
- 预测期价值:- V_1=∑_t = 1^n(R_0×(1 + g_1)^t)/((1 + r)^t)- 其中R_0为评估基准日的收益额,g_1为预测期(前n年)的增长率,r 为折现率,t为预测期的年份(t = 1,2,·s,n)。
- 后续期价值:- 首先计算第n+1年的收益额R_n + 1=R_0×(1 + g_1)^n×(1+g_2)。
- 后续期价值V_2=frac{R_n + 1}{r - g_2}×(1)/((1 + r)^n)。
- 最终企业整体价值V = V_1+V_2。
三、公式中各参数的确定。
1. 收益额R- 收益额可以是净利润、净现金流量等。
在确定收益额时,需要对企业的财务状况进行分析,考虑收入、成本、费用等各项因素的影响。
对于不同的企业和评估目的,可能选择不同的收益额指标。
例如,对于一些注重现金流的企业,净现金流量可能是更合适的收益额指标;而对于关注盈利水平的企业,净利润可能更适用。
2. 增长率g₁和g₂- g₁(预测期增长率)的确定:- 可以通过分析企业所处行业的发展趋势、企业自身的发展战略、市场份额的变化、新产品的开发等因素来确定。
例如,如果企业处于新兴行业,且有多项新产品即将投放市场,可能预计有较高的g₁。
- g₂(稳定期增长率)的确定:- 一般来说,g₂应不高于宏观经济的长期增长率。
可以参考国家的GDP增长率、行业的平均增长率等因素。
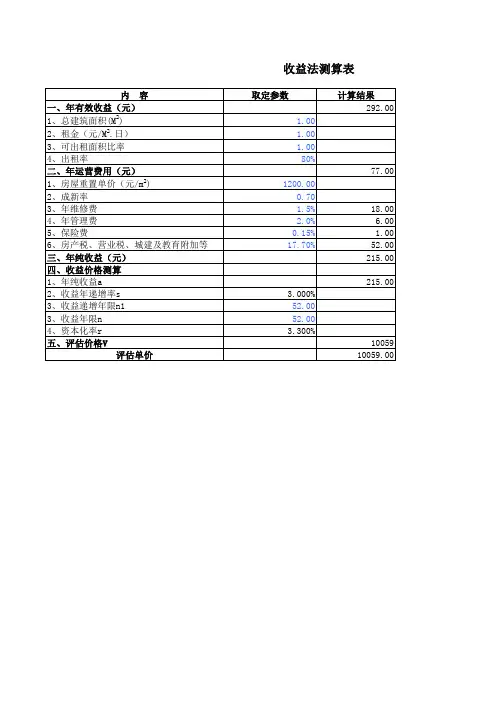
收益法计算公式及应用举例(三)计算公式1.评估房地合一的不动产的价值(L+B)不动产价值(L+B)=不动产净收益/综合资本化率r(4-10)式中,不动产净收益=不动产总收益-不动产总费用根据不动产获取收益的方式时不同,可分为出租型不动产、商业经营型不动产、生产经营型不动产等类型,每种类型不动产净收益的计算方法各有不同。
2.单独评估土地的价值L(1)由土地收益评估土地价值(空地出租)(2)建筑物价值扣除法(3)建筑物收益扣除法3.单独评估建筑物的价值建筑物价值B=不动产价值(L+B)-土地使用权价值L(4-14)建筑物价值B=(不动产净收益-土地净收益)/建筑物资本化率r(4-15)2【说明】(1)不动产总费用并不包含不动产折旧费。
(2)以上所列计算公式均假设土地使用年期为无限年期,但在评估实践中,应注意土地使用的有限年期,以便进行相应的有限年期计算。
(3)在选取估值模型时应注意区分报酬资本化法和直接资本化法。
(四)应用举例1.不动产概况评估对象位于某市某区,建成于2005年,用途为商业,总楼层为地上3层,地下1层,总建筑面积为地上6009.77平方米、地下1898.99平方米。
评估对象(1)位置状况。
评估对象用地四至为:东至永安路,北至道路,西侧为基督教会,南侧为永清大街。
(2)权益状况。
根据委托人提供的《房屋所有权证》(证号略),评估对象设计用途为商业。
地号(略),土地使用权类型为出让,土地使用权终止日期2043年7月30日,土地使用权面积为2145.14平方米。
评估基准日未设定他项权利。
(3)实物状况。
根据评估专业人员现场勘查,评估对象建筑物的装修标准及设备设施情况:钢混结构、外墙刷涂料,地下一层和地上一层地面铺瓷砖,石膏板吊顶,墙面刮大白。
地上二至三层地面铺地板,石膏板吊顶,墙面贴瓷砖。
供水、供电,照明系统,防火分区消防自动喷淋系统,给排风系统等。
(4)基础设施状况。
评估对象宗地红线内基础设施状况达到“六通”(即通路、通电、通讯、通上水、通下水、通热力)。