内插法计算表格

内插法计算表

根据规范
X1 Y1 X2 Y2 计算表格↓ X 待求值
两次内插法计算（粉）
X1 Y1 Y Y2 对应值过程值 (自动计算) 对应值待求值 X X2 对应值过程值 (自动计算) 对应值计算表格↓ 0.55 0.75 170 179.5 162.65 135
表格图例说明↑ 7 150 9 180
7.7
160.5
表格图例说明↑ 0.5 0.9 0.921 1 说明：黄色绿色蓝色红色 190 183.7 160
说明：黄色根据规范值填写绿色为试验统计成果值红色为待求值
Y Y1 Y Y 2 1 X X1 X 2 X1
Y2 Y1 Y Y1 X X1 X 2 X1
根据规范值填写为试验统计成果值自动计算，不需要填写为待求值
两次内插法计算（残）
X1 Y1 Y Y2 对应值过程值 (自动计算) 对应值待求值 X X2 对应值过程值 (自动计算) 对应值计算表格↓ 0.6 0.75 240 217.6 205.2 200
表格图例说明↑ 0.5 0.7 0.787 0.8 说明：黄色绿色蓝色红色 265 225.85 220

内插法计算公式

内插法计算公式
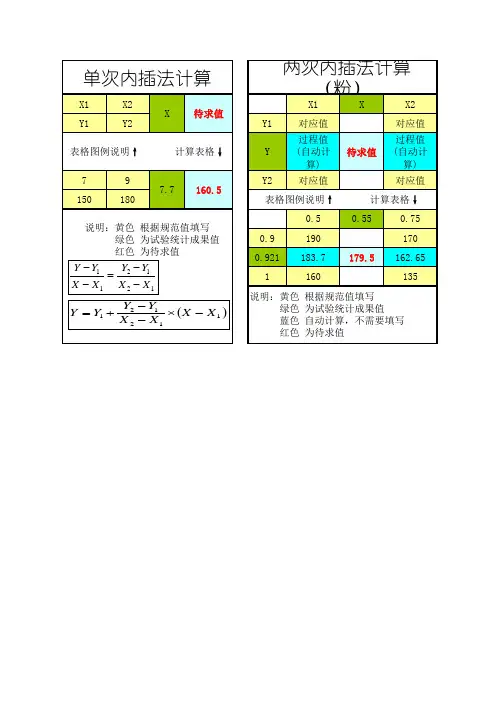
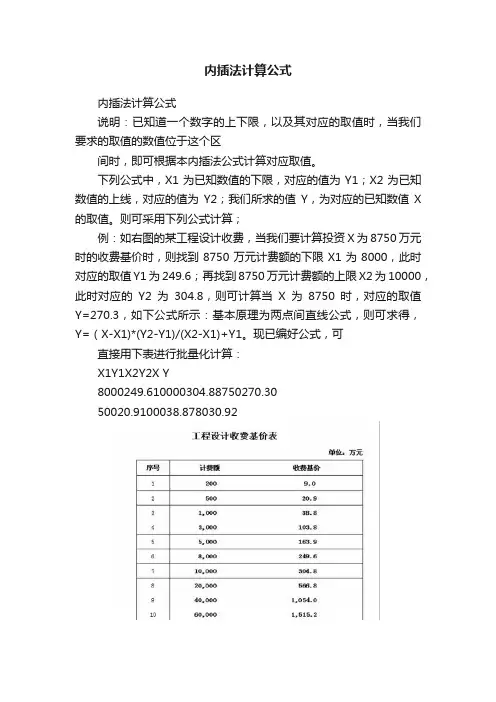
内插法计算公式
说明：已知道一个数字的上下限，以及其对应的取值时，当我们要求的取值的数值位于这个区
间时，即可根据本内插法公式计算对应取值。

下列公式中，X1为已知数值的下限，对应的值为Y1；X2为已知数值的上线，对应的值为Y2；我们所求的值Y，为对应的已知数值X 的取值。

则可采用下列公式计算；
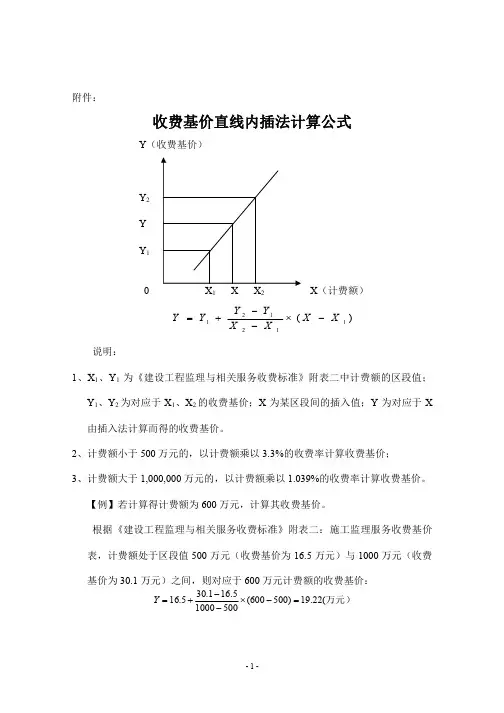
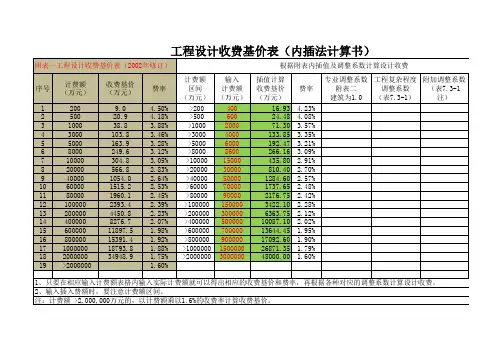
例：如右图的某工程设计收费，当我们要计算投资X为8750万元时的收费基价时，则找到8750万元计费额的下限X1为8000，此时对应的取值Y1为249.6；再找到8750万元计费额的上限X2为10000，此时对应的Y2为304.8，则可计算当X为8750时，对应的取值Y=270.3，如下公式所示：基本原理为两点间直线公式，则可求得，Y=（X-X1)*(Y2-Y1)/(X2-X1)+Y1。

现已编好公式，可
直接用下表进行批量化计算：
X1Y1X2Y2X Y
8000249.610000304.88750270.30
50020.9100038.878030.92。

内插法计算公式工程预算.pdf

-2-
附件：
收费基价直线内插法计算公式
Y（收费基价）
Y2 Y Y1
0
X1 X X2
X（计费额）
Y
Y1
Y2 Y1 ( X X2 X1
X 1)
说明：
1、X1、Y1 为《建设工程监理与相关服务收费标准》附表二中计费额的区段值； Y1、Y2 为对应于 X1、X2 的收费基价；X 为某区段间的插入值；Y 为对应于 X 由插入法计算而得的收费基价。
收费基价 16.5 30.1 78.1 120.8 181.0 218.6 393.4 708.2 99I．4 1255.8 1507.0 2712.5 4882.6 6835.6 8658.4 10390.1
注：计费额大于 1000000 万元的，以计费额乘以 1．039％的收费率计算收费基价。其他未包含的其收费由双方协商议定。
2
3、计费额大于 1,000,000 万元的，以计费额乘以 1.039%的收费率计算收费基价。
【例】若计算得计费额为 600 万元，计算其收费基价。
根据《建设工程监理与相关服务收费标准》附表二：施工监理服务收费基价
表，计费额处于区段值 500 万元（收费基价为 16.5 万元）与 1000 万元（收费
基价为 30.1 万元）之间，则对应于 600 万元计费额的收费基价： Y 16.5 30.1 16.5 (600 500) 19.22(万元） 1000 500
-1-
附表二
序号 1 2 3 4 5 6 7 8 9 10 ll 12 13 14 15 16
施工监理服务收费基价表计费额 500 1000 3000 5000 8000 10000 20000 40000 60000 80000 100000 200000 400000 600000 800000 1000000

第二章内插法

h 10 13.4 20
α
3
6.2
12.3
4
4.6
9.3
4.4
5.8
5
3.7
7.4
z
=z00+
z10 x1
- z 00 - x0
(x
-
x0)+
z 01 y1
-
z 00 y0
(y
-
y0 )
Z ＝4.6＋ 9.3－4.6 20-10
(13.4－10）＋
3.7－4.6 5-4
（4.4－4）＝5.8
n
mile
y1
c
代替曲线进行内插，即以
y
d
弦代替曲线进行内插。
f
结论：
y0
a
e
b
1） f（x）为线性函数，求
O
x0
x
x1 x
得的y值没有误差
2) f（x）为非线性函数，
求得的y值有df误差
①：只要在误差允许的范围内，均可采用线性内插。 ②：对非线性函数，表间距越小，利用线性内插求得的函数值的误差越小。但是表的篇幅会增大。
y＝f（x）
引数 x0
x1 …
函数值 yo
y1 …
比例内插公式：
y
y-y0 y1 -y0
＝xx1--xx00
y1
y
y ＝y0＋xx1--xx00 （y1－y0） y0
＝y0＋y1 x1
-y0 -x0
（x－x0）
O
f(x) c
d
a
e
x0
x
b x1 x
y
f(x) 比率内插的几何意义：
用表列引数两点的直线

1.2第二章内插法

比例双内插的简便算法
X
Y y0 y1 z00 z01 z10 z11
x0
x1
- z 00 z10 - z 00 z 01 z =z00+ (x - x 0 ) + (y - y 0 ) x1 - x 0 y1 - y 0
例2－1－3：求h＝13.4m，α＝4.4时的D？
h 10 6.2 4.6 3.7 13.4 20 12.3 9.3 7.4
（2）求α＝5′，h＝13.4m时的D2？
α h 3 4 5 10 6.2 4.6 3.7 13.4 20 12.3 9.3 7.4
5.0
7 .4 - 3 .7 D1-D 0 D1＝D0＋（h－h0）＝3.7＋ 20 - 10（13.4－10）＝5.0n mile h1-h0
2. 比例反内插内插的逆运算，y＝f（x），已知y求x？
当函数是非线性函数时，如果用比例内插计算将会导致一定的计算误差，为了尽量减小该误差，则引进了变率内插。
一. 变率单内插（一元函数）利用表中给出的函数变化率进行内插。
dy y＝y0＋（x－x0） dx
例2－2－1：用y＝x2造表，求x＝2.3时的y？
（1）用比例内插 y＝5.5 （2）用x＝2变率内插 y＝4＋4（2.3－2）＝5.2 （3）用x＝3变率内插 y＝9＋6（2.3－3）＝4.8 （4）用y＝x2直接计算 y＝5.29
例2－1－1：设物标高h，垂直角α，水平
距离D＝h ctgα，利用该式编表2-1-2如下：（1）求α＝4′，h＝13.4m时的D1？
α h 3 4 5 10 6.2 4.6 3.7 13.4 6.2 20 12.3 9.3 7.4
9 . 3 - 4 .6 D1-D 0 D1＝D0＋（h－h0）＝4.6＋ 20 - 10（13.4－10）＝6.2n mile h1-h0

工程设计收费内插法计算表(2019)

的收费基价和费率，再根据各种对应的调整系数计算设计收费。Fra bibliotek收费基价。
工程设计收费基价表（内插法计算书）
附表一工程设计收费基价表（2002年修订）序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 计费额（万元） 200 500 1000 3000 5000 8000 10000 20000 40000 60000 80000 100000 200000 400000 600000 800000 1000000 2000000 >2000000 收费基价（万元） 9.0 20.9 38.8 103.8 163.9 249.6 304.8 566.8 1054.0 1515.2 1960.1 2393.4 4450.8 8276.7 11897.5 15391.4 18793.8 34948.9 费率 4.50% 4.18% 3.88% 3.46% 3.28% 3.12% 3.05% 2.83% 2.64% 2.53% 2.45% 2.39% 2.23% 2.07% 1.98% 1.92% 1.88% 1.75% 1.60% 计费额区间（万元） >200 >500 >1000 >3000 >5000 >8000 >10000 >20000 >40000 >60000 >80000 >100000 >200000 >400000 >600000 >800000 >1000000 >2000000 输入计费额（万元） 400 600 2000 4000 6000 8600 15000 30000 50000 70000 90000 150000 300000 500000 700000 900000 1500000 3000000 根据附表内插值及调整系数计算设计收费插值计算收费基价（万元） 16.93 24.48 71.30 133.85 192.47 266.16 435.80 810.40 1284.60 1737.65 2176.75 3422.10 6363.75 10087.10 13644.45 17092.60 26871.35 48000.00 费率 4.23% 4.08% 3.57% 3.35% 3.21% 3.09% 2.91% 2.70% 2.57% 2.48% 2.42% 2.28% 2.12% 2.02% 1.95% 1.90% 1.79% 1.60% 专业调整系数工程复杂程度附加调整系数附表二调整系数（表7.3-1 建筑为1.0 （表7.3-1）注）

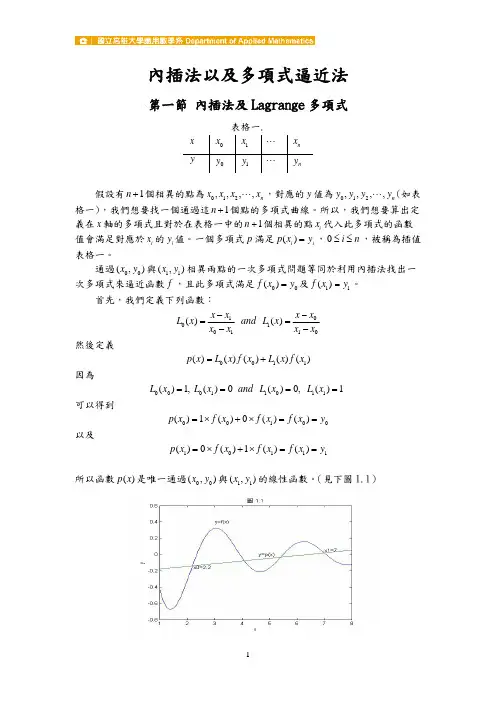
内插法以及多项式逼近法

這個多項式稱為 n 次的 Lagrange 插値多項式，此多項式定義於下列定理中：定理 1.1 如果有 x0 , x1 , x2 ,L , xn 共 n + 1 個相異的點且 f 為ㄧ函數，其函數値由 n + 1 個相異的點給定，則唯一存在一個維度最高為 n 次的多項式 p( x) ，對於 k = 0,1,L , n 使得 f ( xk ) = p ( xk ) 。此多項式為：
這個例子中我們造了一個函數 Ln ,k ( x) 滿足當 i ≠ k ， Ln ,k ( xi ) = 0 以及 Ln ,k ( xk ) = 1 。為了滿足當 i ≠ k ， Ln ,k ( xi ) = 0 ， Ln ,k ( x) 的分子必須為：
( x − x0 )( x − x1 )L ( x − xk −1 )( x − xk +1 )L ( x − xn )
p( x) = L0 ( x) f ( x0 ) + L1 ( x) f ( x1 )
因為
L0 ( x0 ) = 1, L0 ( x1 ) = 0 and L1 ( x0 ) = 0, L1 ( x1 ) = 1
可以得到
p( x0 ) = 1× f ( x0 ) + 0 × f ( x1 ) = f ( x0 ) = y0
內插法以及多項式逼近法
第ㄧ節內插法及 Lagrange 多項式
x
x0
表格一. L x1
xn
y
y0
y1
L
yn
假設有 n + 1 個相異的點為 x0 , x1 , x2 ,L , xn ，對應的 y 値為 y0 , y1 , y2 ,L , yn (如表格一)，我們想要找一個通過這 n + 1 個點的多項式曲線。所以，我們想要算出定義在 x 軸的多項式且對於在表格ㄧ中的 n + 1 個相異的點 xi 代入此多項式的函數值會滿足對應於 xi 的 yi 値。一個多項式 p 滿足 p( xi ) = yi ， 0 ≤ i ≤ n ，被稱為插値表格ㄧ。通過 ( x0 , y0 ) 與 ( x1 , y1 ) 相異兩點的一次多項式問題等同於利用內插法找出一次多項式來逼近函數 f ，且此多項式滿足 f ( x0 ) = y0 及 f ( x1 ) = y1 。首先，我們定義下列函數： x − x0 x − x1 L0 ( x) = and L1 ( x) = x0 − x1 x1 − x0 然後定義

线性内插法

线性内插法是指两个量之间如果存在线性关系，若A（X1，Y1）,B（X2，Y2）为这条直
线上的两个点，已知另一点P 的Y0 值，那么利用他们的线性关系即可求得P 点的对应值X0。

通常应用的
是点P 位于点A、B 之间，故称“线性内插法”。

在求解X0 时，可以根据下面方程计算：
（X0- X1）/(X2 - X1)= (Y0- Y1)/(Y2 - Y1)。

在具体应用中，关键是要搞清楚6 个量X1，Y1，X2，Y2，X0，Y0 之间的关系。

（1）“内插法”的原理是根据等比关系建立一个方程，然后解方程计算得出所要求的数据。

（2）仔细观察方程会看出一个特点，即相对应的数据在等式两方的位置相同。

例如：X1 位于等式左方
表达式的分子和分母的右侧，与其对应的数字Y1 应位于等式右方的表达式的分子和分母的右侧。

（3）应该注意的是，如果对X1 和X2 的数值进行交换，则必须同时对Y1 和Y2 的数值也交换，否则，计
算结果一定不正确。

总的原则是直线上任意两点间的变量X 差值之比应等于对应的变量Y 的差值之比。

内插法在财务管理[2,3],投资决策[4- 6]，古代历法[7]等领域都有广泛的应用.
举个例子，已知X1=1时Y1=3，X3=3时Y3=9，那么x=2时用线性插值得到y就是3和9的算术平均数6。

wps内插法计算公式

wps内插法计算公式
在WPS表格软件中，内插法是一种用于填充数据的方法。

内插法计算公式可以根据不同的内插方法而有所不同。

一般来说，线性插值和多项式插值是两种常见的内插方法。

1. 线性插值公式：
如果要在两个已知数据点之间进行线性插值，可以使用以下公式：
y = y1 + (x x1) ((y2 y1) / (x2 x1))。

其中，(x1, y1)和(x2, y2)是已知的数据点，(x, y)是要进行插值的点。

2. 多项式插值公式：
多项式插值通常使用拉格朗日插值法或牛顿插值法。

以拉格朗日插值为例，假设有n个已知数据点(x1, y1), (x2, y2), ..., (xn, yn)，则可以使用以下公式进行插值：
f(x) = y1 L1(x) + y2 L2(x) + ... + yn Ln(x)。

其中，Lk(x)是拉格朗日基函数，用于将已知数据点进行插值。

以上是WPS表格软件中内插法的计算公式的简要介绍。

不同的内插方法可能有不同的公式，具体使用时需要根据实际情况选择合适的内插方法和相应的计算公式。

内插法计算公式及例题

内插法计算公式及例题1. 什么是内插法？内插法是一种数值计算方法，用于在已知数据点的基础上，通过插值来推算在数据点外部的值。

它广泛应用于物理、工程、地理、金融等领域中。

常见的内插法有拉格朗日内插法、牛顿内插法等。

2. 拉格朗日内插法计算公式假设已有 n+1 个数据点(x0,y0), (x1,y1), …… (xn,yn)，那么拉格朗日插值多项式的形式为L(x)= y0L0(x) + y1L1(x) + …… + ynLn(x)其中，Ln(x)=∏i≠n(xi-x)/(xn-xi)L0(x), L1(x), ……, Ln(x)都是x的一次多项式。

例如，已知以下数据点：x | 1 | 3 | 6 | 9 | 12----------------------------------y | 3 | 5 | 2 | 7 | 1那么可以得到拉格朗日插值多项式为：L(x) = 3(-1/4)x^4 + 2x^3 + 9/4x^2 - 15/4x + 3用这个多项式可以估算出在 x=4 或 x=7.5 时的 y 值。

3. 牛顿内插法计算公式牛顿内插法也是一种常见的内插法，它的插值多项式为：f(x) = f(x0) + f[x0,x1](x-x0) + f[x0,x1,x2](x-x0)(x-x1) + …… +f[x0,x1,…,xn](x-x0)(x-x1)……(x-xn-1)其中，f[x0,x1], f[x0,x1,x2], ……, f[x0,x1,…,xn]是用递推算法求出的差商，它们可以表示为：f[xi] = fif[xi,xi+1] = (fi+1 - fi) / (xi+1 - xi)f[xi,…,xi+k] = (f[xi+1,… xi+k] - f[xi,…,xi+k-1]) / (xk - x0)例如，已知以下数据点：x | 4 | 10 | 15 | 20 | 22------------------------------------y | 2 | 5 | 10 | 15 | 20那么可以得到牛顿插值多项式为：f(x) = 2 + 0.25(x-4) + 0.088(x-4)(x-10) + 0.038(x-4)(x-10)(x-15) + 0.025(x-4)(x-10)(x-15)(x-20)用这个多项式可以估算出在 x=12 或 x=18 时的 y 值。

直线内插法

直线内插法(设计费)(总2页)
--本页仅作为文档封面，使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
附件：
收费基价直线内插法计算公式
)(112121X X X X Y Y Y Y -⨯--+
=
说明： 1、X1、Y1为《工程设计收费标准》附表一中计费额的区段值；Y1、Y2为对应于X1、X2的收费基价；X 为某区段间的插入值；Y 为对应于X 由插入法计算而得的收费基价。

2、计费额＞2000000万元的，以计费额乘以%的收费率计算收费基价。

；
【例】若计算得计费额为270万元，计算其设计收费基价。

根据《工程设计收费标准》附表一：工程设计收费基价表，计费额处于区段值200万元（收费基价为9万元）与500万元（收费基价为万元）之间，则对应于270万元计费额的收费基价：
万元）(78.11)200270(200
50099.209=-⨯--+=Y
Y
Y 2 Y Y 1
工程设计收费按照下列公式计算
1 工程设计收费＝工程设计收费基准价×（1±浮动幅度值）
2 工程设计收费基准价＝基本设计收费＋其他设计收费
3 基本设计收费＝工程设计收费基价×专业调整系数×工程复杂程度调整系。

内插法的计算公式-内插法计算公式

内插法（Interpolation Method）什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率，即租赁利率的方法中，内插法是在逐步法的基础上，找到两个接近准确答案的利率值，利用函数的连续性原理，通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数，求得在函数值为零时的折现率，就是租赁利率。

内插法原理数学内插法即“直线插入法”。

其原理是，若A(i1,b1),B(i2,b2)为两点，则点P（i,b)在上述两点确定的直线上。

而工程上常用的为i在i1,i2之间，从而P在点A、B之间，故称“直线内插法”。

数学内插法说明点P反映的变量遵循直线AB反映的线性关系。

上述公式易得。

A、B、P三点共线，则(b-b1)/(i-i1)＝（b2-b1)/(i2-i1)=直线斜率，变换即得所求。

内插法的具体方法求得满足以下函数的两个点，假设函数为线性函数，通过简单的比例式求出租赁利率。

以每期租金先付为例，函数如下：A表示租赁开始日租赁资产的公平价值；R表示每期租金数额；S表示租赁资产估计残值；n表示租期；r表示折现率。

通过简单的试错，找出二个满足上函数的点（a1，b1）（a2，b2），然后，利用对函数线性的假设，通过以下比例式求出租赁利率：内插法应用举例内插法在财务管理中应用很广泛，如在货币时间价值的计算中，求利率i，求年限n;在债券估价中，求债券的到期收益率；在项目投资决策指标中，求内含报酬率。

中级和CPA教材中都没有给出内插法的原理，很多同学都不太理解是怎么一回事。

下面我们结合实例来讲讲内插法在财务管理中的应用。

一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。

内含报酬率是使投资项目的净现值等于零时的折现率，通过内含报酬率的计算，可以判断该项目是否可行，如果计算出来的内含报酬率高于必要报酬率，则方案可行；如果计算出来的内含报酬率小于必要报酬率，则方案不可行。

标准表修正值计算

标准修正值计算
目前，常用“内插法”即“直线插入法”计算标准器具的修正值，下面介绍“内插法”计算其修正值的原理：
标准读数值
标准修正值
A
y B
y
图1 “内插法”计算修正值的原理图
),(A A y x A )和),(B B y x B 两点的坐标已知，采用“内插法”时，在A 、B 两点确定的直线上的任意一点),(y x P 的坐标值将满足下式：
)(A A
B A
B A x x x x y y y y -⨯--+
= 在计量检定/校准工作中，将校准/检定时标准器具的读数值作为坐标x ，其修正值作为y 。

举例：
工作器具（气温传感器）校准结果表
注：铂电阻标准温度计校准结果通常给出的是其误差值，而其修正值应与误差值符号相反
由于10组标准数据的平均值为23.36℃，则应在表2中（20.07，0.00）和（30.34，-0.02）两点构成的直线上，则此时标准温度表的修正值y 为：
01
.0006.029.327.1002.0)
07.2036.23(07.2034.3000
.002.000.0-≈-=⨯-=-⨯---+
=y。

合集下载