下载文档原格式
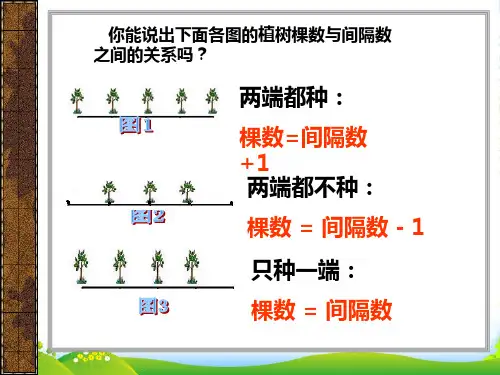
第七单元 植树问题(1)两端都种：棵数=间隔数+1(2)两端不种：棵数 = 间隔数－1(4)封闭图形:棵树 = 间隔数(3)一端种一端不种:棵数 =间隔数知识点一：两端都栽的植树问题植树问题基本解决思路：间隔数=总长÷间隔距离两端都栽：棵数=间隔数＋1知识点二：两端都不栽的植树问题两端不栽：棵数=间隔数－1知识点三：封闭图形的植树问题一端栽一端不栽：棵数=间隔数在一条首尾相接的封闭曲线上植树,所需棵数与间隔数“一一对应”,相当于线段上一端栽一端不栽的情况。
【易错典例1】在一条长300米的公路两边种树,每隔5米种一棵（两端都种）．一共种（）棵树．A．61B．121C．122【思路引导】利用植树问题公式：如果植树路线的两边与两端都植树,那么植树的棵数应比要分的段数多1,再乘2,即：棵数＝（段数+1）×2．根据植树棵数先求段数：300÷5＝60（段）,然后求植树棵数：（60+1）×2计算即可．【完整解答】解：（300÷5+1）×2＝（60+1）×2＝61×2＝122（棵）答：一共种树122棵．故选：C．【考察注意点】本题主要考查植树问题,关键是分清段数和植树棵数的关系做题．【易错典例2】（•红安县期末）一个圆形水池的周长为150米,沿池边每隔37.5米安盏观景灯,一共要安装4盏观景灯．【思路引导】根据题意,在圆形上植树,植树的棵数与间隔数相等,直接用150除以37.5即可．【完整解答】解：根据题意可得：150÷37.5＝4（盏）答：一共需要装4盏灯．故答案为：4．【考察注意点】在封闭线路上植树,棵数与间隔数相等,即：棵数＝间隔数．【易错典例3】操场上等距离放了8张课桌,把相邻的两张课桌用一段绳子连接起来,一共要准备7段绳子．【思路引导】根据题意相当于两端都不植树的问题,用课桌的张数减去1,就是一共要准备的绳子的段数．【完整解答】解：8﹣1＝7（段）答：一共要准备7段绳子．【考察注意点】如果植树线路的两端都不植树,那么植树的棵数比要分的段数少1,即：棵数＝间隔数﹣1．【易错典例4】为庆祝“六一“儿童节,学校在48米长的走廊两边摆鲜花,现在从走廊的一头开始,每隔4米摆一盆鲜花,直至走廊另一头,一共要摆多少盆鲜花？【思路引导】先看一边,据题意可知,走廊长48米,每隔4米摆一盆花,也就是48米被平均分成4米长的若干小段,花摆在分点上；所以间隔数是48÷4＝12个；又因为两端都摆花,所以盆数等于段数加1；然后再乘2就可求出两边的花盆数．【完整解答】解：（48÷4+1）×2＝13×2＝26（盆）答：一共要摆26盆鲜花．【考察注意点】此题属于植树问题．解答此类题（两端都植树）的关键要知道：植树的棵数应比要分的段数多1,即：棵数＝间隔数+1．一．选择题1．（•眉山月考）一条马路长440米,在路的两旁每隔8米植一颗树,两端都要植,共植了（）棵。
五年级上7.2封闭图形的植树问题《五年级上 72 封闭图形的植树问题》在我们的日常生活中，植树是一项非常有意义的活动。
而在数学世界里，植树问题也是一个有趣且实用的知识领域。
今天，让我们一起来探索五年级上册 72 节中封闭图形的植树问题。
首先，我们来明确一下什么是封闭图形。
封闭图形就像是一个圆圈，或者是一个长方形、正方形等，它们的首尾是相连的，没有开口。
比如说，一个圆形的花坛，一个正方形的池塘四周，这都属于封闭图形。
那么在封闭图形中植树，又有什么规律和特点呢？我们先来看一个简单的例子。
假设有一个圆形的花坛，周长是 20 米，每隔 5 米种一棵树，那么一共能种多少棵树呢？我们来算一算。
因为是在封闭图形上植树，所以树的数量和间隔的数量是相等的。
这个圆形花坛的周长是 20 米，每隔 5 米一个间隔，那么间隔数就是 20÷5 ＝ 4（个），所以树的数量也是 4 棵。
再比如一个正方形的池塘，边长是 12 米，每隔 3 米种一棵树，四个角都种，一共要种多少棵树呢？我们先算出每条边的间隔数：12÷3 ＝ 4（个）。
因为正方形有四条边，所以总间隔数就是 4×4 ＝ 16（个）。
但是要注意，由于四个角的树都被重复计算了一次，所以实际上树的数量就是 16 4 ＝ 12（棵）。
通过这两个例子，我们可以总结出封闭图形植树问题的公式：植树的棵数＝间隔数。
那为什么在封闭图形中，植树的棵数会等于间隔数呢？这其实很好理解。
想象一下我们围着一个圆形的操场跑步，起点和终点是重合的。
在这种情况下，跑过的间隔数和经过的位置数是一样的。
植树也是同样的道理，在封闭图形上，树就相当于跑步时经过的位置，间隔就相当于跑过的距离。
掌握了封闭图形的植树问题，对我们的生活也有很大的帮助呢。
比如说，在规划一个公园的时候，如果要在湖边种一排树，知道了湖的周长和树的间隔距离，就能很快算出需要种多少棵树，从而合理安排预算和人力。
再比如，要在一个圆形的广场周围安装路灯，如果知道了广场的周长和路灯之间的间隔，也能轻松算出需要安装多少盏路灯，让广场在夜晚能够明亮又美观。
5-1-3.植树问题（一）教学目标1．封闭与非封闭植树路线的讲解及生活运用。
2．掌握空心方阵和实心方阵的变化规律．3．几何图形的设计与构造知识点拨一、植树问题分两种情况：（一）不封闭的植树路线.①若题目中要求在植树的线路两端都植树，则棵数比段数多1.全长、棵数、株距之间的关系就为：棵数=段数1+=全长÷株距1+全长=株距⨯(棵数1-)株距=全长÷(棵数1-)②如果题目中要求在路线的一端植树，则棵数就比在两端植树时的棵数少1，即棵数与段数相等.全长、棵数、株距之间的关系就为：全长=株距⨯棵数；棵数=段数=全长÷株距；株距=全长÷棵数.③如果植树路线的两端都不植树，则棵数就比②中还少1棵.全长、棵数、株距之间的关系就为：棵数=段数1-=全长÷株距1-.株距=全长÷(棵数1+).全长=株距⨯(棵数+1)（二）封闭的植树路线.在圆、正方形、长方形、闭合曲线等上面植树，因为头尾两端重合在一起，所以种树的棵数等于分成的段数. 全长、棵数、株距之间的关系就为：棵数=段数=周长÷株距.二、解植树问题的三要素（1）总路线长（2）间距（棵距）长（3）棵数，只要知道这三个要素中任意两个要素，就可以求出第三个．三、方阵问题（1）明确空心方阵和实心方阵的概念及区别.（2）每边的个数＝总数÷41+”；（3）每向里一层每边棋子数减少2；（4）掌握计算层数、每层个数、总个数的方法，及每层个数的变化规律。
例题精讲【例 1】大头儿子的学校旁边的一条路长400米，在路的一边从头到尾每隔4米种一棵树，一共能种几棵树？【考点】直线上的植树问题【难度】1星【题型】解答【解析】从图上可以看出，每隔4米种一棵树，如果20米长的路的一边共种了6棵树，这是因为我们首先要在这条路的一端种上一棵，就是说种树的棵树要比间距的个数多1，所以列式为：400÷4+1=101（棵）. 【答案】101棵【巩固】在一条长240米的水渠边上植树，每隔3米植1棵。
假期思维题： 类型一：植树问题植树问题要注意以下情况：1、两侧：两侧都种； 一侧种，另一侧不种。
2、两端的分类情况: 两端都种：棵树=空数+1一端种，另一端不种：棵数=空数两端都不种：棵数=空数-13、封闭图形：棵数=空数7月1日1、 马路的一侧种树，且两端都种。
若每隔5米种一棵树，马路长30米，一共能种多少棵树？2、 马路的两侧种树，且两端都种。
若每隔5米种一棵树，一共能种20棵树，马路长多少米？7月2日马路的一侧安路灯。
（1） 一端有路灯，另一端没有，若每隔4米安一盏灯，马路长40米，可以安多少盏灯？（2） 两端都没有路灯，若每隔6米安一盏灯，共安12盏灯，马路长多少米？7月3日学校有一个圆形水池。
（1） 水池外的周长是40米。
如果绕着水池每隔4米种一棵树，一共能种多少棵树？（2） 水池内的周长为30米。
如果绕着水池内共有10个换水孔，且相邻两个换水孔的距离相等，相邻的两个换水孔间的距离是多少米？7月4日有如图三条马路。
现在要在马路的一侧种树，且每条马路的两端都种树。
已知北路长40米，5米种一棵树，一共能种多少棵树？7月道路两侧插红旗，且两端都要插。
若每隔6米插一面，马路有24米，一共要插多少面红旗？ 7月6日马路的两侧种树，且两端都不种。
若每隔3米种一棵树，马路有30米，一共要种多少棵树？ 7月7日鸟巢外一周共有1000米，绕着鸟巢的一周有灯和树。
（1） 如果每两盏灯之间的距离是5米，鸟巢外一周有多少盏灯？（2） 如果鸟巢外共有250棵树，且相邻两棵树的距离相等，相邻两棵树之间的距离是多少米？7月8日在如图所示的两条马路的一侧安路灯，且每条马路的两端都不安路灯，若每隔9米安一盏路盏路灯，已知北路长81米，西路长多少米？。
封闭植树问题公式
封闭图形的植树问题的公式是棵数=间隔数、棵树=周长÷间距、棵树=长度÷间距+1(两端都栽)、棵树=长度÷间距-1(两端都不栽)、棵树=长度÷间距(一端栽、一端不栽)。
在封闭图形上进行植树，段数等于株数，满足的公式和直线型仅在路的一端植树是一样的：株数=段数=全长÷株距，全长=株距×株数，株距=全长÷株数。
解植树问题首先要判断地形，分清是否封闭图形，从而确定是沿线段植树还是沿周长植树，然后按基本公式进行计算。
将封闭图形“化曲为直”后，发现封闭图形和在不封闭图形“一头种”中棵数和间隔数的关系是一样的，都是棵数等于间隔数。
请注意，在解答具体问题时，应结合题目的实际情况选择合适的公式进行计算。
