检验临界值DW分布-dw检验临界值表教学提纲

2014-2015学年第二学期《数学建模B》第四次论文*员：** 20122641雷翕茜 20122624王伟清 20122628*师：**教学班号： 42015年06月投资额与国民经济摘要本文首先利用了互联网数据，研究四川地区投资额与国民生产总值及物价指数的关系，并对未来国民生产总值及物价指数的估计预测未来的实际投资额。

由于投资额、国民生产总值、物价指数等许多经济变量均有一定的滞后性，因此，在这样的时间序列数据中，同一变量的顺序观测值之间可能出现自相关。

本文用D-W检验诊断数据不存在自相关现象，然后建立回归模型对投资额与国民生产总之及物价指数的关系，最终根据现行预测了未来的国民生产总值及物价指数的估计预测未来的实际投资额。

其次，本文选择了国民经济的一个方面——房地产方面，通过房地产投资额和房地产投资额年增长比率这两个指标对房地产投资规模进行分析。

建立模型，利用计算机Matlab定量评估投资额对GDP的影响，最后还对其惊醒了平稳性ADF 检验，协整分析，物差修正和Granger因果检验。

较为有依据地定量评估了房地产投资额对经济发展的影响关键词:投资额国民生产总值回归模型房地产1、问题重述问题一：利用互联网数据，研究四川地区投资额与国民生产总值及物价指数的关系，并对未来国民生产总值及物价指数的估计预测未来的实际投资额。

问题二：选择国民经济的某个方面，如铁路建设、房地产，建立模型定量评估投资额对经济发展的影响。

2、问题分析问题一：第一问要求研究四川地区投资额与国民生产总值及物价指数的关系，并对未来国民生产总值及物价指数的估计预测未来的实际投资额。

数据是以时间为序的，称时间序列数据。

由于投资额、国民生产总值、物价指数等许多经济变量均有一定的滞后性，比如，前期的投资额对后期投资额一般有明显的影响。

因此，在这样的时间序列数据中，同一变量的顺序观测值之间的出现相关现象（称自相关）是很自然的。

然而，一旦数据中存在这种自相关序列，如果仍采用普通的回归模型直接处理，将会出现不良后果，其预测也会失去意义，为此，我们必须诊断数据是否存在自相关，如果存在，就要考虑自相关关系，建立新的回归模型。

DW检验（Durbin-Watson Test）是一种用于检测时间序列数据自相关性的统计方法。

以下是进行DW检验的步骤：
1. 准备数据：首先，需要准备一个时间序列数据，包括一系列连续的时间点和相应的数据值。

2. 建立回归模型：根据数据构建线性回归模型，包括常数项和解释变量。

3. 计算DW统计量：根据回归模型，计算残差（预测值与实际值之间的差）的平方和RSS。

然后，计算DW统计量，公式为DW = (n - 2) * RSS / (n * σ^2)，其中n为样本数量，σ^2为残差的方差。

4. 查找DW值：在给定的显著水平α下，查找DW值的上界（du）和下界（dL）。

这两个值是根据样本容量n和解释变量个数k'查表得到的。

5. 判断自相关性：将计算得到的DW值与上下界进行比较。

如果DW值接近du，说明不存在自相关性；如果DW值接近dL，说明存在自相关性。

6. 结果解释：根据DW检验的结果，判断回归模型中是否存在自相关性。

如果存在自相关性，可能需要对模型进行调整，如添加滞后项或使用其他建模方法。

需要注意的是，DW检验有一些局限性，如对高阶自相关性的检测能力较弱，不适用于含有缺失数据或复杂数据结构的样本。

在实际应用中，可以根据实际情况选择其他适用于的时间序列分析方法。

附表（临界值表）附表1 符号检验界域表附表2 二项分布表()∑=---=≤xk kn k p p k n k n x X P 01)!(!!)(附表3 标准正态分布表[])(1)(21)(22Z z dweZ W ZΦ-=-Φ-Φ-∞-?π附表4 威尔科克森带符号的秩和检验临界值（T值）表这里T是最大整数，即P（T≤t/n）≤a累积的单尾概率附表5 秩和检验临界值表括号数值表示样本容量（n1,n2）附表6 曼.怀特尼检验（U的临界值）单尾0.025或双尾0.05单尾0.05或双尾0.1附表7 游程检验的临界值表附表8 关于最长游程检验的临界值表当n1,n2≤25时,W a的值P(W≥W a)≤a Ⅰa=0.01Ⅱa=0.05附表9 游程长度平方和检验的临界值表附表10 X2分布表本表对自由度n的X2分布给出上侧分位数(X2a)表，P(X2n>X2a)=α附表11 Kolmogorov—Smirnov拟合优度检验临界值D n表附表12 Kolmogorov----Smirnov双样本检验中D的分子K D的临界值表(小样本) n1=n2≤30附表12续 Kolmogorov----Smirnov双样本检验中D的临界值表附表13 Spearman检验统计量的临界值近似右尾临界值r s*；P(r s>r s*)≤a；n=4--30注意：r s*的相应左尾临界值为-r s*附表14 Kendall检验统计量的临界值当n>60时,T的近似数可以由下式得到：W p≌X p18)52)(1(+-nnn式中X p的值可以从标准正态分布中得到。

上表中只给出肯达尔统计检验量T的数值W p，即T的数值的上界，而下界数可由以下关系式得出：W p=-W p临界域为：T>W p或T<-W p附表15 Kendall协和系数中S的临界值表附表16 Cruskall---Wallis检验统计量的临界值附表17 上、下游程分布的数目。

用于检验序列相关的DW统计量的取值范围
Durbin-Watson统计量（简称DW统计量）是一种常用来检验序列相关性的统计指标，主要用在时间序列分析中。

她由Durbin和Watson 在1950年发明，是个介于0 ~ 4之间的统计量，也可以视作2阶自相关。

DW统计量的范围是0 ~ 4，其中该指标取0或4的可能性比较小，但可以推出如果随机模型的DW检验（DW Test）的临界值不同，那么原来的取值范围也会改变，如果DW检验的临界值为2，得到的DW的范围是一般是小于2的，此时可以推断出序列有自相关性，如果DW检验的临界值是3，则DW的范围一般会大于3，此时可以推断出序列没有自相关性。

一般来说，DW检验会介于[-2，2]之间，当值接近0时，说明该序列存在一定的自相关性，此时所拟合的模型可能是错误的。

当DW统计量处于[-2，2]之间时，说明模型中存在自相关结构，此时可以通过改进模型来消除自相关结构。

总之，Durbin-Watson统计量的取值范围是介于0~4之间，但根据具体的序列相关性不同，可改变[-2，2]之间的临界值，如果DW检验的临界值是2，则其范围会改变到0 ~ 2之间，如果DW检验的临界值是3，则其范围会改变到3 ~ 4之间。

当值处于[-2，2]之间时，一般认为存在自相关结构，此时可以通过改进模型来消除自相关结构。

dw检验临界值表
dw检验临界值表是用来确定抽样单元离散警戒点的统计检验方法，可用于检测状态变化。

它通常用于检测变量的机器学习或控制，也可以检测发生不同类型的异常行为。

一、背景介绍
dw检验是根据特定的假设条件，采用传统的概率统计学将假设检验应用至可以采用连续变量来描述的过程检验的方法。

一般来说，dw检验会产生一组临界值，这些值用来检验变量的变化，检验是否离散警戒点。

二、准备条件
1、数据要求：dw检验要求被检测变量为连续值，且需另外分组定义正常或异常状态，以判断其波动范围。

2、模型设置：在dw检验过程中，需定义数据的空间分布，即假设条件如何定义，检验原理是否可信等。

三、临界值表
dw检验所得到的临界值表是以T或z值来表示的，其结果与分析结果有关，以下是一个示例表格：
拒绝域T值z值
α=0.05 1.645 1.96
α=0.01 2.326 2.33
α=0.001 3.090 3.09
对于不同置信水平，临界值是有差别的，在解释这些结果时，大多数情况下会给出T值，而罕见情况下则为z值。

T值和z值都具有双尾拒绝域，这决定了可接受的最大随机误差。

四、总结
dw检验临界值表是用来确定抽样单元离散警戒点的统计检验方法，可用于检测状态变化。

通过dw检验得到临界值时，一般会用T或z值来表示，而这些值可以用来判断变量是否出现警戒点，从而确定是否出现异常。

DW检验表-dw检验表完整版Durbin-Watson Statistic: 5 Per Cent Significance Points of dL and dU k'=1k'=2k'=3k'=4k'=5k'=6k'=7k'=8k'=9k'=10 n dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU 60.6101.400------------------------------------------------------------------------------------------70.7001.3560.4671.896--------------------------------------------------------------------------------80.7631.3320.5591.7770.3672.287----------------------------------------------------------------------90.8241.3200.6291.6990.4552.1280.2962.588------------------------------------------------------------100.8791.3200.6971.6410.5252.0160.3762.4140.2432.822--------------------------------------------------110.9271.3240.7581.6040.5951.9280.4442.2830.3152.6450.2033.004----------------------------------------120.9711.3310.8121.5790.6581.8640.5122.1770.3802.5060.2682.8320.1713.149------------------------------131.0101.3400.8611.5620.7151.8160.5742.0940.4442.3900.3282.6920.2302.9850.1473.266--------------------141.0451.3500.9051.5510.7671.7790.6322.0300.5052.2960.3892.5720.2862.8480.2003.1110.1273.360----------151.0771.3610.9461.5430.8141.7500.6851.9770.5622.2200.4472.4710.3432.7270.2512.9790.1753.2160.1113.438精品Durbin-Watson Statistic: 5 Per Cent Significance Points of dL and dU k'=1k'=2k'=3k'=4k'=5k'=6k'=7k'=8k'=9k'=10 n dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU161.1061.3710.9821.5390.8571.7280.7341.9350.6152.1570.5022.3880.3982.6240.3042.8600.2223.0900.1553.304171.1331.3811.0151.5360.8971.7100.7791.9000.6642.1040.5542.3180.4512.5370.3562.7570.2722.9750.1983.184181.1581.3911.0461.5350.9331.6960.8201.8720.7102.0600.6032.2580.5022.4610.4072.6680.3212.8730.2443.073191.1801.4011.0741.5360.9671.6850.8591.8480.7522.0230.6492.2060.5492.3960.4562.5890.3692.7830.2902.974201.2011.4111.1001.5370.9981.6760.8941.8280.7921.9910.6912.1620.5952.3390.5022.5210.4162.7040.3362.885211.2211.4201.1251.5381.0261.6690.9271.8120.8291.9640.7312.1240.6372.2900.5462.4610.4612.6330.3802.806221.2391.4291.1471.5411.0531.6640.9581.7970.8631.9400.7692.0900.6772.2460.5882.4070.5042.5710.4242.735231.2571.4371.1681.5431.0781.6600.9861.7850.8951.9200.8042.0610.7152.2080.6282.3600.5452.5140.4652.670241.2731.4461.1881.5461.1011.6561.0131.7750.9251.9020.8372.0350.7502.1740.6662.3180.5842.4640.5062.613251.2881.4541.2061.5501.1231.6541.0381.7670.9531.8860.8682.0130.7842.1440.7022.2800.6212.4190.5442.560精品Durbin-Watson Statistic: 5 Per Cent Significance Points of dL and dU k'=1k'=2k'=3k'=4k'=5k'=6k'=7k'=8k'=9k'=10 n dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU261.3021.4611.2241.5531.1431.6521.0621.7590.9791.8730.8971.9920.8162.1170.7352.2460.6572.3790.5812.513精品Durbin-Watson Statistic: 5 Per Cent Significance Points of dL and dUk'=1k'=2k'=3k'=4k'=5k'=6k'=7k'=8k'=9k'=10 n dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU271.3161.4691.2401.5561.1621.6511.0841.7531.0041.8610.9251.9740.8452.0930.7672.2160.6912.3420.6162.470281.3281.4761.2551.5601.1811.6501.1041.7471.0281.8500.9511.9590.8742.0710.7982.1880.7232.3090.6492.431291.3411.4831.2701.5631.1981.6501.1241.7431.0501.8410.9751.9440.9002.0520.8262.1640.7532.2780.6812.396301.3521.4891.2841.5671.2141.6501.1431.7391.0711.8330.9981.9310.9262.0340.8542.1410.7822.2510.7122.363311.3631.4961.2971.5701.2291.6501.1601.7351.0901.8251.0201.9200.9502.0180.8792.1200.8102.2260.7412.333321.3731.5021.3091.5741.2441.6501.1771.7321.1091.8191.0411.9090.9722.0040.9042.1020.8362.2030.7692.306331.3831.5081.3211.5771.2581.6511.1931.7301.1271.8131.0611.9000.9941.9910.9272.0850.8612.1810.7962.281341.3931.5141.3331.5801.2711.6521.2081.7281.1441.8081.0791.8911.0151.9780.9502.0690.8852.1620.8212.257351.4021.5191.3431.5841.2831.6531.2221.7261.1601.8031.0971.8841.0341.9670.9712.0540.9082.1440.8452.236精品Durbin-Watson Statistic: 5 Per Cent Significance Points of dL and dUk'=1k'=2k'=3k'=4k'=5k'=6k'=7k'=8k'=9k'=10 n dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU361.4111.5251.3541.5871.2951.6541.2361.7241.1751.7991.1141.8761.0531.9570.9912.0410.9302.1270.8682.216371.4191.5301.3641.5901.3071.6551.2491.7231.1901.7951.1311.8701.0711.9481.0112.0290.9512.1120.8912.197381.4271.5351.3731.5941.3181.6561.2611.7221.2041.7921.1461.8641.0881.9391.0292.0170.9702.0980.9122.180391.4351.5401.3821.5971.3281.6581.2731.7221.2181.7891.1611.8591.1041.9321.0472.0070.9902.0850.9322.164401.4421.5441.3911.6001.3381.6591.2851.7211.2301.7861.1751.8541.1201.9241.0641.9971.0082.0720.9522.149451.4751.5661.4301.6151.3831.6661.3361.7201.2871.7761.2381.8351.1891.8951.1391.9581.0892.0221.0382.088501.5031.5851.4621.6281.4211.6741.3781.7211.3351.7711.2911.8221.2461.8751.2011.9301.1561.9861.1102.044551.5281.6011.4901.6411.4521.6811.4141.7241.3741.7681.3341.8141.2941.8611.2531.9091.2121.9591.1702.010601.5491.6161.5141.6521.4801.6891.4441.7271.4081.7671.3721.8081.3351.8501.2981.8941.2601.9391.2221.984精品Durbin-Watson Statistic: 5 Per Cent Significance Points of dL and dUk'=1k'=2k'=3k'=4k'=5k'=6k'=7k'=8k'=9k'=10 n dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU651.5671.6291.5361.6621.5031.6961.4711.7311.4381.7671.4041.8051.3701.8431.3361.8821.3011.9231.2661.964 701.5831.6411.5541.6721.5251.7031.4941.7351.4641.7681.4331.8021.4011.8381.3691.8741.3371.9101.3051.948 751.5981.6521.5711.6801.5431.7091.5151.7391.4871.7701.4581.8011.4281.8341.3991.8671.3691.9011.3391.935精品Durbin-Watson Statistic: 5 Per Cent Significance Points of dL and dUk'=1k'=2k'=3k'=4k'=5k'=6k'=7k'=8k'=9k'=10 n dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU dL dU801.6111.6621.5861.6881.5601.7151.5341.7431.5071.7721.4801.8011.4531.8311.4251.8611.3971.8931.3691.925 851.6241.6711.6001.6961.5751.7211.5501.7471.5251.7741.5001.8011.4741.8291.4481.8571.4221.8861.3961.916 901.6351.6791.6121.7031.5891.7261.5661.7511.5421.7761.5181.8011.4941.8271.4691.8541.4451.8811.4201.909 951.6451.6871.6231.7091.6021.7321.5791.7551.5571.7781.5351.8021.5121.8271.4891.8521.4651.8771.4421.903 1001.6541.6941.6341.7151.6131.7361.5921.7581.5711.7801.5501.8031.5281.8261.5061.8501.4841.8741.4621.898 1501.7201.7471.7061.7601.6931.7741.6791.7881.6651.8021.6511.8171.6371.8321.6221.8461.6081.8621.5931.877 2001.7581.7791.7481.7891.7381.7991.7281.8091.7181.8201.7071.8311.6971.8411.6861.8521.6751.8631.6651.874如有侵权请联系告知删除，感谢你们的配合！精品如有侵权请联系告知删除，感谢你们的配合！精品。

小样本DW统计量的分布特征张晓峒1赵初晓2(1. 南开大学国际经济研究所, 天津 300071)(2. 天津大学管理学院, 天津 300072)摘要：本文用模特卡罗模拟方法研究了样本容量在54以下的DW统计量的分布特征，并给出小样本DW检验临界值表。

同时用DW检验提出了一个判别最小二乘估计中是否存在虚假回归的有效方法。

关键词：模特卡罗模拟，DW分布，非平稳性，协整Distribution of Small Sample DW StatisticZhang Xiaotong1Zhao Chuxiao2(1. Institute of International Economics, Nankai University, Tianjin 300071)(2. Management School, Tianjin University, Tianjin 300072)Abstract In this paper we investigated the DW distribution with sample size under 54 byMonte Carlo simulation method and gave a critical table for small sample DW test. Basedon that we proposed a method for recognizing spurious regression in ordinary least squaresestimation.Keywords: Monte Carlo simulation, DW distribution, nonstationary, cointegration1．概述八十年代以来，Engle-Granger (1987), Engle-Yoo (1987) 和Sargan-Bhargava (1983)都曾提及用DW统计量检验非平稳变量间的协整性问题。

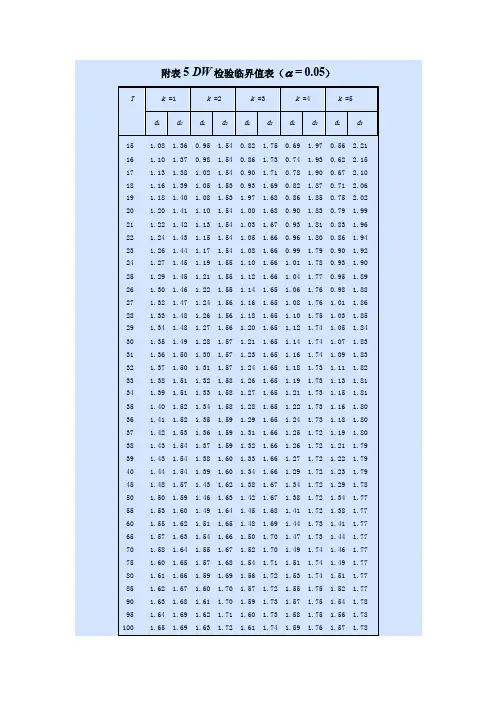
附表5 DW检验临界值表（ = 0.05）T k =1k =2k =3k =4 k =5d L dUdLdUdLdUdLdUdLdU15 1.08 1.360.95 1.540.82 1.750.69 1.970.56 2.2116 1.10 1.370.98 1.540.86 1.730.74 1.930.62 2.1517 1.13 1.38 1.02 1.540.90 1.710.78 1.900.67 2.1018 1.16 1.39 1.05 1.530.93 1.690.82 1.870.71 2.0619 1.18 1.40 1.08 1.53 1.97 1.680.86 1.850.75 2.0220 1.20 1.41 1.10 1.54 1.00 1.680.90 1.830.79 1.9921 1.22 1.42 1.13 1.54 1.03 1.670.93 1.810.83 1.9622 1.24 1.43 1.15 1.54 1.05 1.660.96 1.800.86 1.9423 1.26 1.44 1.17 1.54 1.08 1.660.99 1.790.90 1.9224 1.27 1.45 1.19 1.55 1.10 1.66 1.01 1.780.93 1.9025 1.29 1.45 1.21 1.55 1.12 1.66 1.04 1.770.95 1.8926 1.30 1.46 1.22 1.55 1.14 1.65 1.06 1.760.98 1.8827 1.32 1.47 1.24 1.56 1.16 1.65 1.08 1.76 1.01 1.8628 1.33 1.48 1.26 1.56 1.18 1.65 1.10 1.75 1.03 1.8529 1.34 1.48 1.27 1.56 1.20 1.65 1.12 1.74 1.05 1.8430 1.35 1.49 1.28 1.57 1.21 1.65 1.14 1.74 1.07 1.8331 1.36 1.50 1.30 1.57 1.23 1.65 1.16 1.74 1.09 1.8332 1.37 1.50 1.31 1.57 1.24 1.65 1.18 1.73 1.11 1.8233 1.38 1.51 1.32 1.58 1.26 1.65 1.19 1.73 1.13 1.8134 1.39 1.51 1.33 1.58 1.27 1.65 1.21 1.73 1.15 1.8135 1.40 1.52 1.34 1.58 1.28 1.65 1.22 1.73 1.16 1.8036 1.41 1.52 1.35 1.59 1.29 1.65 1.24 1.73 1.18 1.8037 1.42 1.53 1.36 1.59 1.31 1.66 1.25 1.72 1.19 1.8038 1.43 1.54 1.37 1.59 1.32 1.66 1.26 1.72 1.21 1.7939 1.43 1.54 1.38 1.60 1.33 1.66 1.27 1.72 1.22 1.7940 1.44 1.54 1.39 1.60 1.34 1.66 1.29 1.72 1.23 1.79 45 1.48 1.57 1.43 1.62 1.38 1.67 1.34 1.72 1.29 1.78 50 1.50 1.59 1.46 1.63 1.42 1.67 1.38 1.72 1.34 1.77 55 1.53 1.60 1.49 1.64 1.45 1.68 1.41 1.72 1.38 1.77 60 1.55 1.62 1.51 1.65 1.48 1.69 1.44 1.73 1.41 1.77 65 1.57 1.63 1.54 1.66 1.50 1.70 1.47 1.73 1.44 1.77 70 1.58 1.64 1.55 1.67 1.52 1.70 1.49 1.74 1.46 1.77 75 1.60 1.65 1.57 1.68 1.54 1.71 1.51 1.74 1.49 1.77 80 1.61 1.66 1.59 1.69 1.56 1.72 1.53 1.74 1.51 1.77 85 1.62 1.67 1.60 1.70 1.57 1.72 1.55 1.75 1.52 1.77 90 1.63 1.68 1.61 1.70 1.59 1.73 1.57 1.75 1.54 1.78 95 1.64 1.69 1.62 1.71 1.60 1.73 1.58 1.75 1.56 1.78 100 1.65 1.69 1.63 1.72 1.61 1.74 1.59 1.76 1.57 1.78注：1. 表示检验水平，T表示样本容量，k表示回归模型中解释变量个数（不包括常数项）。