DW值判断准则
- 格式:doc
- 大小:109.00 KB
- 文档页数:2

dw统计量的取值范围
dw统计量的取值范围
dw统计量,指的是数学统计学中用来描述研究对象特征的一种分类指标,也
被称为$DFW(Description Flow Width)。它的本质是运用数学语言描述某个对象
的特征,用以说明该对象的特性和关系。相对来说,它的取值范围要比其他统计指
标更丰富、更容易理解。
dw统计量取值范围通常是数学定义的,从最大值到最小值;它也可以是一个
从序数型中取值的范围;它也可以是从集合中取值;此外,还可以是从空间上取值;
甚至可以是以可视化形式取值。另外,dw统计量的取值范围还可以是从变量的范
围内取值;最后,也可以从响应时间的分布中取值。
总的来说,dw统计量的取值范围是一个十分广阔的范围,可以根据特定的研
究需求和特定的研究对象,来优选最合适的取值范围,获取最丰富的数据,以得出
最准确的结论和有效的解决方案。

dw检验方法啥是 dw 检验方法呀?这可真是个挺专业的玩意儿呢!其实啊,它就像是我们生活中的一个小侦探,专门来帮我们看看数据之间是不是存在着一些猫腻。
想象一下,我们有一堆数据,就好像是一群调皮的小孩子,有时候它们会乖乖的,但有时候也会捣乱。
那 dw 检验方法呢,就是来判断这些数据乖不乖的工具。
它能告诉我们数据有没有那种自相关的问题。
啥叫自相关呢?就好比你走路,一步一步很有规律,这就是一种自相关。
数据要是有自相关,那就可能会影响我们对结果的判断呢。
比如说,我们研究一个现象,根据这些数据得出了一个结论。
但如果数据有自相关,那这个结论可能就不那么靠谱啦,就好像你根据一个人今天穿什么颜色的衣服,就说他以后每天都穿这个颜色,这不是有点荒唐嘛!那 dw 检验方法具体是咋工作的呢?它会通过一些计算和分析,给我们一个数值。
这个数值就像是一个信号灯,告诉我们数据的情况。
如果数值在一个特定范围内,那就说明数据没啥大问题,我们可以放心使用;要是不在这个范围内,那可得小心了,得重新审视这些数据。
你可能会问,这有啥难的呀,不就是算个数嘛。
嘿,可别小瞧它,这里面的门道可多着呢!就像做菜一样,同样的食材,不同的人做出来味道可不一样。
dw 检验方法也是,不同的人用可能会得出不一样的结果,这就得靠经验和技巧啦。
而且啊,这可不是一锤子买卖。
有时候我们还得反复用这个方法,就像给数据做体检一样,一次不放心就多检查几次。
这样才能确保我们得出的结论是可靠的呀。
在实际应用中,dw 检验方法可是帮了大忙呢!比如在经济学、统计学等领域,它能让我们更准确地分析数据,做出更合理的决策。
就像一个聪明的军师,为我们出谋划策。
总之呢,dw 检验方法虽然有点专业,但它真的很重要。
它就像是我们在数据世界里的导航仪,帮助我们找到正确的方向,避免我们在错误的道路上越走越远。
所以啊,大家可别小看了它哟!现在,你对dw 检验方法是不是有了更清楚的认识啦?。

DW检验的实施步骤1. 确定研究目的在进行DW检验之前,首先需要明确研究的目的是什么。
DW检验一般用于评估两个或多个相关样本或处理组之间是否存在差异。
2. 收集数据收集与研究目的相关的数据,并对数据进行整理和清洗。
确保数据的准确性和完整性,并进行必要的数据预处理,如缺失值处理和异常值处理。
3. 确定检验的类型根据研究目的和收集到的数据,确定使用哪种类型的DW检验。
常见的DW检验类型包括独立样本DW检验、配对样本DW检验和重复测量DW检验。
•独立样本DW检验适用于比较两个相互独立的样本或处理组之间的差异。
•配对样本DW检验适用于比较同一组个体或样本在不同时间点或处理条件下的差异。
•重复测量DW检验适用于比较同一组个体或样本在多个处理条件下的差异。
4. 假设检验进行DW检验之前,需要提出研究假设并进行假设检验。
DW检验的零假设表示样本或处理组之间不存在差异,备择假设表示样本或处理组之间存在差异。
5. 计算DW统计量根据所选的DW检验类型和收集到的数据,通过计算DW统计量来评估样本或处理组之间的差异。
•对于独立样本DW检验,计算的是两个样本或处理组的DW统计量。
•对于配对样本DW检验,计算的是同一组个体或样本在不同时间点或处理条件下的DW统计量。
•对于重复测量DW检验,计算的是同一组个体或样本在多个处理条件下的DW统计量。
6. 判断显著性通过与相应的临界值比较DW统计量来判断样本或处理组之间的差异是否显著。
如果DW统计量大于临界值,则拒绝零假设,认为样本或处理组之间存在显著差异。
7. 结果解释根据显著性判断的结果,进行结果的解释和分析。
说明样本或处理组之间的差异的方向和程度,并讨论可能的原因和影响。
8. 结论和建议根据分析的结果和讨论,得出结论并提出相应的建议。
结论应该回答研究目的,并基于实际的研究结果做出合理的推断。
以上是DW检验的实施步骤,通过按照这些步骤进行操作,可以对样本或处理组之间的差异进行评估和分析。

dw检验的公式推导
DW检验是一种统计方法,用于检验时间序列数据中是否存在自相关性。
其公式推导过程如下:计算样本数据的一阶差分值,即将每个数据点减去前一个数据点的值,得到一个新的时间序列。
然后,计算新时间序列的平方和,即将每个差分值平方并相加。
接下来,将原始时间序列的平方和减去新时间序列的平方和,得到DW统计量的分子。
计算DW统计量的分母,即将新时间序列中每个差分值与其前一个差分值的差值平方并相加,再将结果乘以2。
最终,将DW统计量的分子除以分母,得到DW检验的结果。
若DW值接近于2,则表明时间序列数据不存在自相关性;若DW值偏离2,则表明时间序列数据存在正向或负向的自相关性。
DW检验是一种简单而有效的方法,可用于判断时间序列数据中是否存在自相关性。
通过上述公式推导的过程,我们可以更好地理解DW检验的原理和应用。

stata dw检验命令Stata DW检验命令是统计学中常用的一种方法,用来检验序列数据的平稳性。
DW检验的全称为Durbin-Watson检验,是由统计学家James Durbin和Geoffrey Watson于1951年提出的一种自相关性检验方法。
在时间序列数据分析中,如果变量之间存在自相关性,就会导致数据不满足独立同分布的假设,从而影响到最终的统计推断结果。
在Stata中,可以通过使用“dw”命令进行DW检验。
该命令会输出检验统计量的值,以及对应的临界值,从而帮助我们判断序列数据是否存在自相关性。
一般来说,如果DW统计量的值接近于2,表明序列数据不存在一阶自相关性;如果DW统计量的值远离2,就意味着序列数据存在自相关性。
为了进行DW检验,首先需要导入需要分析的数据集。
在Stata中,可以使用命令“use 文件路径\文件名”来导入数据。
接着,我们可以使用“dw 变量名”来对指定的变量进行DW检验。
Stata会输出DW 统计量的值,以及对应的上下临界值,我们可以通过比较DW统计量与临界值的大小来判断序列数据是否存在自相关性。
除了使用“dw”命令外,我们还可以使用“dwtest”命令进行DW检验。
这个命令会输出更加详细的检验结果,包括DW统计量的值、临界值、p值等信息,帮助我们做出更准确的判断。
需要注意的是,在进行DW检验之前,需要确保数据的时间序列是连续的,没有缺失值。
否则,DW检验的结果可能会出现偏差,影响到最终的分析结论。
总的来说,Stata中的DW检验命令是一种简单而有效的方法,用来检验时间序列数据的自相关性。
通过对DW统计量的计算和比较,我们可以快速判断序列数据是否存在自相关性,为进一步的数据分析提供参考依据。
希望本文对读者们能够有所帮助,谢谢阅读。

dw检验的基本步骤
嘿,咱今儿来聊聊 DW 检验的那些事儿哈!
你知道不,DW 检验就像是一个侦探,要去探寻数据里有没有啥问题呢!那它到底咋个操作呢?
首先呢,咱得把数据准备好呀,就像厨师做菜得先有食材一样。
然后计算出残差,这残差可重要啦,就好比是案件的线索。
接着呢,根据这些残差来计算出一个统计量,这个统计量就像是给线索打分一样。
再然后呀,就把这个统计量和标准的数值范围去比较,看看是在正常范围内呢,还是超出啦。
这就好比判断一个人是好人还是坏人,得有个标准不是?
如果在正常范围内,那就可以松口气啦,说明数据没啥大问题。
但要是超出了,那可就得好好琢磨琢磨啦,是不是哪里出了岔子呀。
你想想看,要是数据有问题,就像盖房子根基没打好,那后面得出的结论能靠谱吗?这可不是闹着玩的呀!
就好比你走路,要是方向偏了一点,可能越走越远,最后都不知道走到哪里去啦。
DW 检验就是帮咱把方向给搞对咯。
咱可不能小瞧了这 DW 检验的基本步骤哦,每一步都得认真对待。
这可不是随便玩玩的,这是关系到整个研究、分析是不是可靠的关键呀!
它就像一个细心的卫士,守护着数据的准确性和可靠性。
没有它,
咱可能就会在数据的海洋里迷失方向,找不到北咯!
所以呀,咱得好好掌握 DW 检验的基本步骤,让它为咱的研究、分
析保驾护航。
别嫌麻烦,这可是为了得到准确结果必须付出的努力呀!你说是不是这个理儿呢?。

(最新版3篇)编写:_______________审核:_______________审批:_______________单位:_______________时间:_______________序言小编为大家精心编写了3篇《简述dw方法检验一阶自相关的方法》,供大家借鉴与参考。
下载后,可根据实际需要进行调整和使用,希望对大家有所帮助。
(3篇)《简述dw方法检验一阶自相关的方法》篇1DW(Durbin-Watson)方法是一种常用的检验一阶自相关的方法,它的基本思想是通过检验残差的序列相关性来判断回归模型中是否存在一阶自相关。
在使用 DW 方法进行自相关检验时,需要满足以下前提条件:1. 回归模型中含有截距项;2. 解释变量是非随机的;3. 随机扰动项是一阶线性自相关;4. 没有缺失数据,样本比较大。
具体操作步骤如下:1. 根据给定的显著水平 a、样本容量 n 和解释变量个数 k",查 D.W.表得到 d 统计量的上界 du 和下界 dL;2. 计算残差的散点图,并将其绘制出来;3. 观察残差散点图,如果图中的点呈现出明显的序列相关性,则说明存在一阶自相关;4. 根据 d 统计量的值与 du、dL 的大小关系,判断自相关的程度及是否存在自相关。
《简述dw方法检验一阶自相关的方法》篇2DW(Durbin-Watson)方法是一种常用的检验一阶自相关的方法,它的基本思想是通过检验残差的序列相关性来判断随机误差项是否存在一阶自相关。
在使用 DW 方法进行自相关检验时,需要满足以下前提条件:1. 回归模型中含有截距项;2. 解释变量是非随机的;3. 随机扰动项是一阶线性自相关;4. 没有缺失数据,样本比较大。
具体操作步骤如下:1. 根据给定的显著水平 a、样本容量 n 和解释变量个数 k",查 D.W.表得到 d 统计量的上界 du 和下界 dL;2. 计算残差的散点图,并将其绘制出来;3. 观察残差散点图,如果图中的点呈现出明显的序列相关性,则说明随机误差项存在一阶自相关;4. 根据 d 统计量的值与 du、dL 的大小关系,判断一阶自相关的程度及是否存在一阶自相关。

DW检验(Durbin-Watson Test)是一种用于检测时间序列数据自相关性的统计方法。
以下是进行DW检验的步骤:
1. 准备数据:首先,需要准备一个时间序列数据,包括一系列连续的时间点和相应的数据值。
2. 建立回归模型:根据数据构建线性回归模型,包括常数项和解释变量。
3. 计算DW统计量:根据回归模型,计算残差(预测值与实际值之间的差)的平方和RSS。
然后,计算DW统计量,公式为DW = (n - 2) * RSS / (n * σ^2),其中n为样本数量,σ^2为残差的方差。
4. 查找DW值:在给定的显著水平α下,查找DW值的上界(du)和下界(dL)。
这两个值是根据样本容量n和解释变量个数k'查表得到的。
5. 判断自相关性:将计算得到的DW值与上下界进行比较。
如果DW值接近du,说明不存在自相关性;如果DW值接近dL,说明存在自相关性。
6. 结果解释:根据DW检验的结果,判断回归模型中是否存在自相关性。
如果存在自相关性,可能需要对模型进行调整,如添加滞后项或使用其他建模方法。
需要注意的是,DW检验有一些局限性,如对高阶自相关性的检测能力较弱,不适用于含有缺失数据或复杂数据结构的样本。
在实际应用中,可以根据实际情况选择其他适用于的时间序列分析方法。

dw检验练习题 一、问题描述与分析 DW检验(Durbin-Watson test)是一种常用的线性回归模型诊断方法,用于判断回归模型中误差项是否存在自相关性。本文将通过一个实例来介绍DW检验的基本原理和应用。
在进行线性回归分析时,我们通常假设误差项满足独立同分布(i.i.d.)的条件,即误差项之间不存在相关性。然而,在实际应用中,误差项之间往往存在一定的相关性,这可能导致参数估计的不准确性和模型诊断结果的不可靠性。
为了判断误差项是否存在自相关性,统计学家Durbin和Watson提出了DW检验方法。DW检验的原假设(H0)是误差项不存在自相关性,备择假设(H1)是误差项存在正向或负向的一阶自相关性。
二、DW检验的计算方法 DW检验通过计算DW统计量来判断误差项的自相关性。DW统计量的取值范围为0到4,理论上近似服从正态分布。若DW统计量接近2,则表明误差项不存在自相关性;若DW统计量接近0或4,则表明误差项存在正向或负向的自相关性。
具体计算DW统计量的方法如下:首先,将回归方程的残差(误差项的估计值)按时间顺序排列,然后计算相邻残差之间的差异值。接下来,将这些差异值的平方和除以残差平方和,即可得到DW统计量。 三、DW检验的实例 为了更好地理解DW检验的应用,我们选择一个实例来进行分析。 假设我们想研究一所中学的学生考试成绩与以下两个变量的关系:学习时间和家庭背景。我们采集了100个学生的数据,并使用线性回归模型进行拟合。
回归方程如下所示: Y = β0 + β1*X1 + β2*X2 + ε 其中,Y代表考试成绩,X1代表学习时间,X2代表家庭背景,β0、β1、β2分别是回归系数,ε代表误差项。
接下来,我们使用统计软件计算回归模型的残差,并进行DW检验。 根据计算结果,DW统计量为1.2,显著大于0且接近2,说明误差项不存在自相关性。因此,我们可以认为学习时间和家庭背景与考试成绩之间的线性回归模型是有效的。

用于检验序列相关的DW统计量的取值范围
Durbin-Watson统计量(简称DW统计量)是一种常用来检验序列相关性的统计指标,主要用在时间序列分析中。
她由Durbin和Watson 在1950年发明,是个介于0 ~ 4之间的统计量,也可以视作2阶自相关。
DW统计量的范围是0 ~ 4,其中该指标取0或4的可能性比较小,但可以推出如果随机模型的DW检验(DW Test)的临界值不同,那么原来的取值范围也会改变,如果DW检验的临界值为2,得到的DW的范围是一般是小于2的,此时可以推断出序列有自相关性,如果DW检验的临界值是3,则DW的范围一般会大于3,此时可以推断出序列没有自相关性。
一般来说,DW检验会介于[-2,2]之间,当值接近0时,说明该序列存在一定的自相关性,此时所拟合的模型可能是错误的。
当DW统计量处于[-2,2]之间时,说明模型中存在自相关结构,此时可以通过改进模型来消除自相关结构。
总之,Durbin-Watson统计量的取值范围是介于0~4之间,但根据具体的序列相关性不同,可改变[-2,2]之间的临界值,如果DW检验的临界值是2,则其范围会改变到0 ~ 2之间,如果DW检验的临界值是3,则其范围会改变到3 ~ 4之间。
当值处于[-2,2]之间时,一般认为存在自相关结构,此时可以通过改进模型来消除自相关结构。
stata dw检验命令
Stata DW检验命令是统计学中常用的一种方法,用来检验时间序列数据是否存在单位根,即数据是否平稳。
在本文中,我们将详细介绍Stata中如何使用DW检验命令来进行单位根检验。
打开Stata软件并导入你的时间序列数据。
接着,在Stata命令窗口中输入以下命令:dwtest 变量名,其中“变量名”为你要进行单位根检验的变量名称。
执行该命令后,Stata会输出Durbin-Watson统计量以及对应的p值。
Durbin-Watson统计量的取值范围为0到4之间。
如果Durbin-Watson统计量接近于2,表明数据存在正自相关性;如果接近于0或4,则表明数据存在负自相关性。
一般来说,Durbin-Watson统计量在1.5到2.5之间,可以认为数据不存在自相关性。
而p值则用来判断DW统计量的显著性。
一般情况下,若p值小于0.05,则可以拒绝原假设,即数据不具有单位根;反之,如果p值大于0.05,则接受原假设,数据具有单位根。
在进行DW检验之前,建议先进行单位根检验,以确保数据的平稳性。
如果数据存在单位根,应该首先对数据进行差分处理,然后再进行DW检验。
除了使用DW检验命令外,Stata还提供了其他单位根检验方法,如ADF检验、PP检验等。
研究人员可以根据具体情况选择合适的方法
进行检验。
Stata DW检验命令是一种简单而有效的方法,用来判断时间序列数据是否具有单位根。
通过对数据进行单位根检验,可以帮助研究人员更准确地分析数据,从而得出更可靠的结论。
希望本文能对您有所帮助。
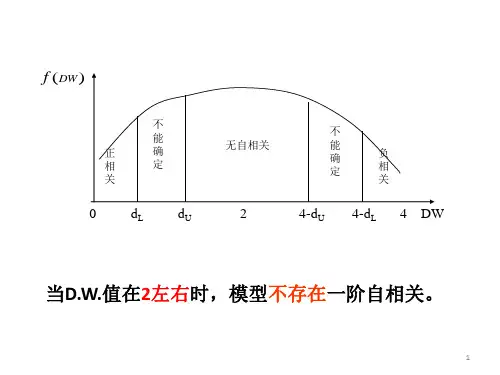
D--W检验
D--W检验,仅适用于一阶自相关的检验。构造统计量:
nttnttteeeDW1
2
2
2
1
)(
(1)
计算该统计量的值,根据样本容量n和解释变量数目k查D-W分布表,得到临界值dl和du, dl du 4-du 即对于相邻的样本点,ie都较大或较小,此时,1iiee较小,DW统计量的分子较小, DW值较小;如果模型存在负自相关,即对于相邻的样本点,若ie较大则1ie较小,若ie较 niinininiiiiieeeeeDW1 (2) 当n较大时,niiniiniieee1222122,,大致相等,则(2)可以化简为: ee n n 如果存在完全一阶负相关,即 ee n n 如果完全不相关,即 ee n n 从判断准则中看到,存在一个不能确定的D.W.值区域,这是这种检验方法的一大缺陷。
然后按照下列准则考察计算得到的DW值,以判断模型的自相关状态。
若 0
不能确定
无自相关
为什么可以通过DW值检验自相关的存在呢?从直观上看,如果模型存在正自相关,
小则1ie较大,此时,1iiee较大,DW统计量的分子较大,DW值也较大;如果模型不
存在自相关,则ie与1ie呈随机关系,此时,1iiee较为适中,则D.W.统计量取一个适
中值。从数学上也容易证明,展开D.W.统计量:
2
222
121
2
2
)ˆ1(2)1(21221niiniiieeeDW
如果存在完全一阶正相关,即
01ˆ1221DW
e
i
i
i
ii
41ˆ1221DW
e
i
i
i
ii
20ˆ1221DW
e
i
i
i
ii
D.W.检验虽然只能检验一阶自相关,但在实际计量经济学问题中,一阶自相关是出现最多
的一类序列相关,而且经验表明,如果不存在一阶自相关,一般也不存在高阶序列相关。所
以在实际应用中,对于序列相关问题一般只进行D.W.检验。