当前位置：文档之家 › 数字信号处理(方勇)第三章习题答案

数字信号处理(方勇)第三章习题答案

  • 格式：doc
  • 大小：2.91 MB
  • 文档页数：49

下载文档原格式

  / 49

合集下载

数字信号处理 Chapter03答案

数字信号处理 Chapter03答案

11
3.2 Properties of the z-Transform
Ex. ( linearity) x(n) = [3(2n) – 4(3n)] u(n) 3 4 – 1 – 2z –1 1 – 3z –1
X(z) =
ROC: |z| > 3
12
3.2 Properties of the z-Transform
z = re
jθ
=
n =−∞
∑ x ( n )r
−n
∞
− n − jθ n
e
X ( z) ≤
n =−∞
∞
∑
−1
x (n) r
+∑
n=0
∞
∞
x ( n) rn
x (n) rn
≤ ∑ x ( −n ) r + ∑
n n =1 n =0
7
3.1 The z-Transform
3.1.1 The Direct z-Transform
3.2 Properties of the z-Transform
X(z) = ∑ x(n) z – n
14
3.2 Properties of the z-Transform
X(z) = ∑ x(n) z – n
15
X(z) = ∑ x(n) z – n
16
3.3 Rational z-Transforms
1 2 −1 1 2 2
X ( z ) = 1+ z + (
X ( z) = 1 1− z
1 2 −1
)
z + .... + (
−2
1 n 2
)
z −n

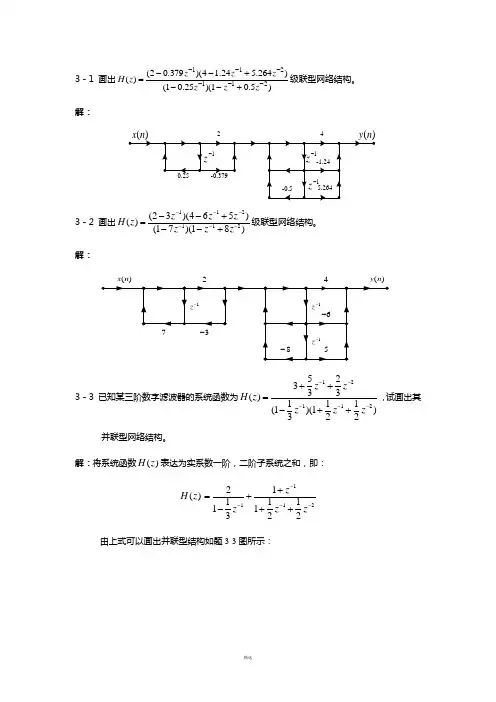
数字信号处理(方勇)第三章习题答案

数字信号处理(方勇)第三章习题答案

3－1 画出)5.01)(25.01()264.524.14)(379.02()(211211------+--+--=z zz z z z z H 级联型网络结构。

解：243－2 画出112112(23)(465)()(17)(18)z z z H z z z z --------+=--+级联型网络结构。

解：()x n ()y n 243－3 已知某三阶数字滤波器的系统函数为1211252333()111(1)(1)322z z H z z z z -----++=-++，试画出其并联型网络结构。

解：将系统函数()H z 表达为实系数一阶，二阶子系统之和，即：()H z 11122111111322z z z z ----+=+-++ 由上式可以画出并联型结构如题3-3图所示：)题3-3图3－4 已知一FIR 滤波器的系统函数为121()(10.70.5)(12)H z zz z ---=-++，画出该FIR滤波器的线性相位结构。

解： 因为121123()(10.70.5)(12)1 1.30.9H z zz z z z z ------=-++=+-+，所以由第二类线性相位结构画出该滤波器的线性相位结构，如题3-4图所示：()x n 1-1-1z -题3-4图3－5 已知一个FIR 系统的转移函数为：12345()1 1.25 2.75 2.75 1.23H z z z z z z -----=+--++求用级联形式实现的结构流图并用MATLAB 画出其零点分布及其频率响应曲线。

解： 由转移函数可知，6=N ，且)(n h 偶对称，故为线性相位系统，共有5个零点，为5阶系统，因而必存在一个一阶系统，即1±=z 为系统的零点。

而最高阶5-z 的系数为+1，所以1-=z 为其零点。

)(z H 中包含11-+z 项。

所以：11()()(1)H z H z z -=+。

1()H z 为一四阶子系统，设12341()1H z bzcz bz z ----=++++，代入等式，两边相等求得12341()10.2530.25H z zz z z ----=+-++，得出系统全部零点，如图3-5（b ）所示。

《数字信号处理》课后答案

《数字信号处理》课后答案

数字信号处理课后答案 1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值； （2）试用延迟单位脉冲序列及其加权和表示()x n 序列； （3）令1()2(2)x n x n =-，试画出1()x n 波形； （4）令2()2(2)x n x n =+，试画出2()x n 波形； （5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14； （2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

数字信号处理课后习题答案(全)1-7章

数字信号处理课后习题答案(全)1-7章

2． 给定信号：
2n+5
－4≤n≤－1
(x(n)=
6
0
0≤n≤4 其它
(1) 画出x(n)序列的波形， 标上各序列值；
(2) 试用延迟的单位脉冲序列及其加权和表示x(n)序列；
第 1 章 时域离散信号和时域离散系统
（3） 令x1(n)=2x(n－2)， 试画出x1(n)波形； （4） 令x2(n)=2x(n+2)， 试画出x2(n)波形； （5） 令x3(n)=x(2－n)， 试画出x3(n)波形。 解： (1) x(n)序列的波形如题2解图（一）所示。 (2) x(n)=－3δ(n+4)－δ(n+3)+δ(n+2)+3δ(n+1)+6δ(n)
第 1 章 时域离散信号和时域离散系统
题8解图（一）
第 1 章 时域离散信号和时域离散系统
x(n)=－δ(n+2)+δ(n－1)+2δ(n－3)
h(n)=2δ(n)+δ(n－1)+ δ(n－2)
由于
x(n)*δ(n)=x(n)
1
x(n)*Aδ(n－k)=Ax(n－k)
2
故
第 1 章 时域离散信号和时域离散系统
y(n)=x(n)*h(n)
=x(n)*［2δ(n)+δ(n－1)+ δ(n－2) 1 2
, 这是2π有理1数4， 因此是周期序
3
（2） 因为ω=
,
所以
1
8
=16π, 这是无理数， 因此是非周期序列。
2π
第 1 章 时域离散信号和时域离散系统
4． 对题1图给出的x(n)要求：
(1) 画出x(－n)的波形；

数字信号处理课后答案课件

数字信号处理课后答案课件
傅里叶变换具有线性、对称性、时移性、频移性等性质，这些性质 在信号处理中具有重要应用。
傅里叶变换的性质
线性性质
若离散信号x(n)和y(n)的 傅里叶变换分别为 X(e^jωn)和Y(e^jωn)， 则对于任意实数a和b，有 aX(e^jωn) + bY(e^jωn) 的傅里叶变换等于 aX(e^jωn)和bY(e^jωn) 的傅里叶变换之和。
从而实现信号的分离、抑制或提 取。
滤波器分类
根据不同的特性，滤波器可分为 低通、高通、带通和带阻滤波器，
每种滤波器都有各自的应用场景 和特点。
滤波器原理
滤波器的原理是基于频率响应， 即不同频率的信号经过滤波器后， 其幅度和相位会发生不同的变化。
IIR滤波器设计
IIR滤波器概述
IIR滤波器设计方法
IIR滤波器稳定性
在设计IIR滤波器时，需要考虑其稳定 性。如果系统函数的极点位于单位圆 外，则系统不稳定，可能会导致无穷 大的输出。因此，在设计过程中需要 进行稳定性分析。
FIR滤波器设计
FIR滤波器概述
FIR（Finite Impulse Response）滤 波器是一种具有有限冲击响应的数字 滤波器，其系统函数可以表示为有限 项之和。
插值法
对于非周期性的连续时间信号，可以通过插值法得到离散时间信号。常用的插值方法包括 线性插值、多项式插值、样条插值等。
傅里叶变换法
对于任何连续时间信号，可以通过傅里叶变换将其转换为频域表示形式，然后对频域表示 形式进行采样，得到离散时间信号。再通过逆傅里叶变换将其转换回时域表示形式。
05 第五章 信号的分 析与合成
抽样定理的充分性
对于任何连续时间信号，如果其最高频率分量小于等于fmax，则可 以通过其抽样信号无失真地重建出原信号。

数字信号处理课后第三章习题答案

数字信号处理课后第三章习题答案

1 e j 0 N
2 j(0 k ) N 1 e
k 0, 1, , N 1
（8） 解法一
直接计算：
1 j 0 n x8 (n) sin(0 n) RN (n) [e e j 0 n ] R N ( n ) 2j
X 8 (n)

n 0
N 1
kn x8 (n)WN
k 0, 1, , N 1
(4)
X (k ) WNkn
n 0
m1
π j ( m1) k 1 WNkm N e 1 WNk
π sin mk N R (k ) N π sin k N
第３章
离散傅里叶变换(DFT)及其快速算法 (FFT)
所以
DFT[ X (n)] X (n)W
n 0
N 1
N 1
kn N
N 1 mn kn x(m)WN WN n 0 m 0
N 1
n ( m k ) x(m)WN m 0 n 0
N 1
第３章
由于
离散傅里叶变换(DFT)及其快速算法 (FFT)
第３章
离散傅里叶变换(DFT)及其快速算法 (FFT)
（10） 解法一
X (k )

n 0
N 1
kn nWN
k 0, 1, , N 1
上式直接计算较难， 可根据循环移位性质来求解X(k)。 因为x(n)=nRN(n)， 所
以
x(n)－x((n－1))NRN(n)+Nδ(n)=RN(n) 等式两边进行DFT， 得到
1 [e j0 n e j0 n ] e 2 j n 0

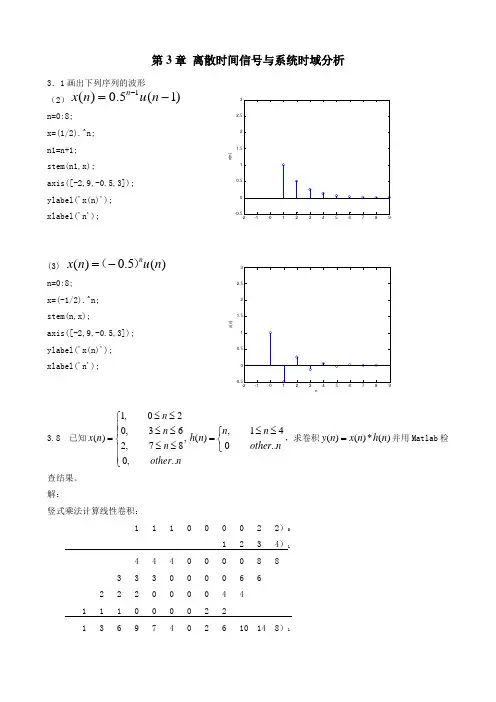
数字信号处理》课后作业参考答案

数字信号处理》课后作业参考答案

第3章 离散时间信号与系统时域分析3．1画出下列序列的波形（2）1()0.5(1)n x n u n -=- n=0:8; x=(1/2).^n;n1=n+1; stem(n1,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');(3) ()0.5()nx n u n =-（）n=0:8; x=(-1/2).^n;stem(n,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');3.8 已知1,020,36(),2,780,..n n x n n other n≤≤⎧⎪≤≤⎪=⎨≤≤⎪⎪⎩,14()0..n n h n other n≤≤⎧=⎨⎩，求卷积()()*()y n x n h n =并用Matlab 检查结果。

解：竖式乘法计算线性卷积： 1 1 1 0 0 0 0 2 2）01 2 3 4）14 4 4 0 0 0 0 8 83 3 3 0 0 0 0 6 62 2 2 0 0 0 0 4 41 1 1 0 0 0 02 21 3 6 9 7 4 02 6 10 14 8）1x (n )nx (n )nMatlab 程序:x1=[1 1 1 0 0 0 0 2 2]; n1=0:8; x2=[1 2 3 4]; n2=1:4; n0=n1(1)+n2(1);N=length(n1)+length(n2)-1; n=n0:n0+N-1; x=conv(x1,x2); stem(n,x);ylabel('x(n)=x1(n)*x2(n)');xlabel('n'); 结果：x = 1 3 6 9 7 4 0 2 6 10 14 83.12 (1) 37πx （n ）=5sin(n) 解：2214337w πππ==，所以N=14 (2) 326n ππ-x （n ）=sin()-sin(n)解：22211213322212,2122612T N w T N w N ππππππ=========，所以(6) 3228n π-x （n ）=5sin()-cos(n) 解：22161116313822222()T N w T w x n ππππππ=======，为无理数，所以不是周期序列所以不是周期序列3.20 已知差分方程2()3(1)(2)2()y n y n y n x n --+-=，()4()nx n u n -=，(1)4y -=，(2)10,y -=用Mtalab 编程求系统的完全响应和零状态响应，并画出图形。

数字信号处理习题第三章

数字信号处理习题第三章

第3章频域中的离散时间信号3.16 求下面每个序列的DTFT:(a) x1[n]=αnμ[n−1],|α|<1(b) x2[n]=nαnμ[n],|α|<1(e) x5[n]= αnμ[−n−1],|α|>1答案：（a）X1(e jω)=∑αn e−jωn∞n=1=∑(αe−jω)n=∞n=1∑(αe−jω)n−1=αe−jω1−αe−jω∞n=0（b）X2(e jω)=j dX(e jω)dω=j ddω(11−αe−jω)=αe−jω(1−αe−jω)2（e）X5(e jω)=∑αn e−jωn=∑α−m e jωm=∑α−m e jωm−1=∞m=0∞m=1−1n=−∞e jωα−e jω3.17 求下面每个序列的DTFT：(a) xa[n]= μ[n+2]−μ[n−3](b) xb[n]=αn(μ[n−1]− μ[n−4]),|α|<1(c) xc[n]= 2nαnμ[n],|α|<1答案：（a）设μ[n]的DTFT变换为：μ(e jω)=11−e−jω+∑πδ(ω+2kπ)∞k=−∞Xa(e jω)=(e j2ω−e−j3ω)μ(e jω)=(e j2ω−e−j3ω)[11−e−jω+∑πδ(ω+2kπ)]∞k=−∞（b）设x[n]= αnμ[n],|α|<1，其DTFT变换为：X(e jω)=11−αe−jωXb (e jω)=e−jωX(e jω)−e−j4ωX(e jω)=e−jω−e−j4ω1−αe−jω（c）xc[n]= 2nαnμ[n]=2(n+1)αnμ[n]−2αnμ[n],|α|<1X C (e jω)=2(1−αe−jω)2−21−αe−jω=2αe−jω(1−αe−jω)23.21 求下面每个DTFT的逆DTFT：(a) Xa (e jω)=∑δ(ω+2πk)∞k=−∞(b) Xb (e jω)=e jω(1−e jωN)1−e jω(c) Xc (e jω)=1+2∑cosωιNι=0(d) Xd (e jω)=−αe−jω(1−αe−jω)2,|α|<1答案：（a） xa [n]=12π∫δ(ω)e jωn∞−∞dω=1（b ） X b (e jω)=e jω(1−e jωN )1−e jω=e jω∑ejωnN−1n=0 令m =−n X(ejω)=∑e−jωm −N+1m=0 x[n]={1,−(N −1)≤n ≤00,其他X b (e jω)=e jω∑e−jωm−N+1m=0=e jωX(e jω) X b [n]=x[n+1]={1,−N ≤n ≤−10,其他（c ）X c (e jω)=1+2∑cosωιN ι=0=2+∑e−jωιN ι=−N , x c [n]={3,n =01,0<|n |<N 0,其他（d ）X 0(e jω)=11−αe −jω x o [n]=αn μ[n]X d (ejω)=−αe −jω(1−αe −jω)2=dX0(e jω)dωx d [n]=n x o [n]=nαn μ[n]3.26 X (e jω)是实序列x[n]的DTFT 。

第三章习题答案1要点

第三章习题答案1要点

第三章习题答案1要点数字信号处理学习拓展3-1画H（z）？解决方案：(2?0.379z?1)(4?1.24z?1?5.264z?2)(1?0.25z)(1?z?1?1?0.5z)?2级联型网络结构。

x（n）z？10.2524y（n）z？1-1.24-0.5-0.379z？十五点二六四(2?3z?1)(4?6z?1?5z?2)3－2画出h(z)?级联型网络结构。

?1?1?2(1?7z)(1?z?8z)解：x（n）24y（n）z？17? 3z？1.6.8z？十五523?z?1?z?2333－3已知某三阶数字滤波器的系统函数为h(z)?，试画出其1?11?11?2(1?z)(1?z?z)322并联型网络结构。

解：系统函数H（z）表示为一阶和二阶子系统的实系数之和，即：21?z?1?h(z)?1?11?11?21?z1?z?z322由上式可以画出并联型结构如题3-3图所示：3-1数字信号处理学习拓展2x（n）1/31z？1y（n）？1/2? 1/2z？1z？十一题3-3图3-4已知FIR滤波器的系统函数为h（z）？（1×10.7z×1×0.5z×2）（1×2Z×1），绘制fir滤波器的线性相位结构。

解决方案：因为H（z）？（1？0.7z？1？0.5z？2）（1？2z？1）？1.1.3z？1.0.9z？2.Z第二类线性相位结构画出该滤波器的线性相位结构，如题3-4图所示：x（n）1z？1z？1z？1y（n）11.3？零点九题3-4图3-5众所周知，FIR系统的传递函数为：h(z)?1?1.25z?1?2.75z?2?2.75z?3?1.23z?4?z?5找到以叶栅形式实现的结构流程图，并用MATLAB绘制其零点分布和频响曲线。

解：由转移函数可知，n?6，且h(n)偶对称，故为线性相位系统，共有5个零点，为5因此，必须有一个一阶系统，也就是Z？？1是系统的零点。

数字信号处理》第三版课后习题答案

数字信号处理》第三版课后习题答案

数字信号处理课后答案教材第一章习题解答1.用单位脉冲序列()nδ及其加权和表示题1图所示的序列。

解：2.给定信号：25,41 ()6,040,n nx n n+-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n序列；（3）令1()2(2)x n x n=-，试画出1()x n波形；（4）令2()2(2)x n x n=+，试画出2()x n波形；（5）令3()2(2)x n x n=-，试画出3()x n波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）（3）1()x n的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n时，先画x(-n)的波形，然后再右移2位，3()x n波形如题2解图（四）所示。

3.判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14；（2）12,168w wππ==，这是无理数，因此是非周期序列。

5.设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

（1）()()2(1)3(2)y n x n x n x n =+-+-； （3）0()()y n x n n =-，0n 为整常数； （5）2()()y n x n =； （7）0()()nm y n x m ==∑。

解：（1）令：输入为0()x n n -，输出为'000'0000()()2(1)3(2)()()2(1)3(2)()y n x n n x n n x n n y n n x n n x n n x n n y n =-+--+---=-+--+--=故该系统是时不变系统。

第3章 完整版习题解答

第3章 完整版习题解答

（2） f

fs N

4096 4096
1Hz
（3）直接用 DFT 计算，所需要的复乘次数为
M d (300 200 1)N 101 4096 413696
若用按时间抽取 FFT 则需要的复乘次数为
MF

N 2
log10
N

2048 12

24576
3.13 下面是三个不同的信号 xi (n) ，每个信号均为两个正弦信号的和：
DFT 在加窗后会有两个可区分的谱峰？
解：利用
64
点
DFT
来估计信号谱时，其频率分辨率为


Hale Waihona Puke 2 64信号 x1 (n) cos( n / 4) cos(17 n / 64) 的两个余弦信号的频率间隔为：
1

17 64

4

64

2 64
故利用 64 点 DFT 来估计信号谱时，不能分辨 x1(n) 中两个正弦信号的谱峰。

2M
时，DIF-FFT
共需
M
级分解，每级运算要计算的碟形运算有
N 2
个。
3.4 考虑图 T3-1 中的蝶形。这个蝶形是从实现某种 FFT 算法的信号流图中取出的。从下述论述中选择出最 准确的一个：
（1）这个蝶形是从一个按时间抽取的 FFT 算法中取出的。 （2）这个蝶形是从一个按频率抽取的 FFT 算法中取出的。 （3）由图无法判断该蝶形取自何种 FFT 算法。

N 2
1
[x(n)
n0

x(n

N 2
)]WNnr/

数字信号处理 答案 第三章

数字信号处理 答案 第三章

解： x1 ( n) 和 x2 (n) 的图形如图 P3.7_1 所示：
3.8 图 P3.8 表示一个 4 点序列 x( n) 。 （1）绘出 x( n) 与 x( n) 的线性卷积结果的图形。 （2）绘出 x( n) 与 x( n) 的 4 点循环卷积结果的图形。 （3）绘出 x( n) 与 x( n) 的 8 点循环卷积结果的图形，并将结果与（1）比较，说明线性卷积与循环卷 积之间的关系。
j [(2π k /10) + (π /10)]
={
3.7
N ,k=m或 k=−m 2 0,其 他
图 P3.7 表示的是一个有限长序列 x( n) ,画出 x1 ( n) 和 x2 (n) 的图形。 （1） x1 ( n) = x ⎡ ⎣( n − 2 ) ⎤ ⎦ 4 R4 (n)
（2） x2 ( n) = x ⎡ ⎣( 2 − n ) ⎤ ⎦ 4 R4 (n)
解： （1） X ( k )
= ∑ δ (n)WNnk = δ (0) = 1, 0 ≤ k ≤ N − 1
n=0
N −1
（2） X ( k ) =
∑ δ [(n − n )]
n =0 0
N −1
N
RN (n)WNnk = WNn0 k , 0 ≤ k ≤ N − 1
（3） （4）
X (k ) = ∑ a W
− jω N
−j
N ω 2
j
N ω 2
−j
N ω 2
⎛N ⎞ sin ⎜ ω ⎟ N −1 ) ⎝ 2 ⎠ e− j 2 ω = sin
ω
2
⎛N ⎞ sin ⎜ ω ⎟ ⎝ 2 ⎠ , ϕ (ω ) = − N − 1 ω | X (e jω ) |= ω 2 sin 2

数字信号处理课后答案第三章3

数字信号处理课后答案第三章3

1e 4

1

(1)k
j k
1e 4
当 k 2,4,6,... 时，X%1(k) 0
序列2: X%2 (k)

2 j nk
e4
n0
j 3 k

1

e

4 j
k
1e 4
当 k 2,4,6,... 时，X%1(k) 0
序列3:
x%3(n) x%1(n) x%1(n 4)
故 f (n)中只有 n 5到 n 14的点对应于 x(n) y(n)
应该得到的点。
10. 已知两个有限长序列为
n 1, 0 n 3
x(n)
0,
4n6
y(n)

1,

1,
0n4 5n6
试用作图表示 x(n) ，y(n)以及 f (n) x(n) ⑦ y(n) 。
又因N必须为2的整数幂，所以一个记录中的
最少点数为 N 210 1024
x((n))5
x((n))6 x((n))6 R6 (n)
x((n 3))5 R5(n)
x((n))3 R3(n) x((n))7 R7 (n)
5. 试求以下有限长序列的N 点DFT（闭合形式表
达式）：
(2) x(n) anRN (n)
N 1
解：X (k) x(n)WNnk RN (k)
根据序列移位性质可知
X%3 (k )

X%1 (k )

e
j k X%1 (k )

(1

ej kΒιβλιοθήκη )1(1)k j k
1e 4

数字信号处理课后习题答案全章

数字信号处理课后习题答案全章
5． 设系统分别用下面的差分方程描述， x(n)与y(n)分别表示系统 输入和输出， 判断系统是否是线性非时变的。
（1）y(n)=x(n)+2x(n－1)+3x(n－2) （2）y(n)=2x(n)+3 （3）y(n)=x(n－n0) n0 （4）y(n)=x(－n)
团结 信赖 创造 挑战
（5）y(n)=x2(n)
因此系统是非时变系统。
团结 信赖 创造 挑战
（5） y(n)=x2(n)
令输入为
输出为
x(n－n0)
y′(n)=x2(n－n0)
y(n－n0)=x2(n－n0)=y′(n)
故系统是非时变系统。 由于
T［ax1(n)+bx2(n)］=［ax1(n)+bx2(n)］2 ≠aT［x1(n)］+bT［x2(n) =ax21(n)+bx22(n)
x(n)=－δ(n+2)+δ(n－1)+2δ(n－3)
h(n)=2δ(n)+δ(n－1)+ δ(n－12)
由于
2
x(n)*δ(n)=x(n)
x(n)*Aδ(n－k)=Ax(n－k)
故
团结 信赖 创造 挑战
y(n)=x(n)*h(n)
=x(n)*［2δ(n)+δ(n－1)+ δ(n－21 ) 2
=2x(n)+x(n－1)+ x1 (n－2) 将x(n)的表示式代入上式， 得到2
解： （1） y(n)=x(n)*h(n)=
R4(m)R5(n－m)
先确定求和域。 由R4(m)和R5(n－mm)确定y（n）对于m的
间如下:
0≤m≤3
－4≤m≤n

数字信号处理课后答案第3和4章

数字信号处理课后答案第3和4章
用DFT/FFT对序列进行频谱分析， 频谱分析范围为π; 用DFT/FFT对模拟信号进行频谱分析， 频谱分析范围为采 样频率的一半， 即0.5Fs。
用DFT/FFT对信号进行谱分析的误差表现在三个方面， 即混叠现象、 栅栏效应和截断效应。 截断效应包括泄漏和 谱间干扰。
第３章 离散傅里叶变换(DFT)及其快速算法
第３章 离散傅里叶变换(DFT)及其快速算法
(FFT)
xN(n)=IDFT［X(k)］为x(n)的周期延拓序列（以N为延拓周期） 的主值序列。 以后这一结论可以直接引用。
［例3.4.2］ 已知 x(n)=R8(n), X(ejω)=FT［x(n)］
对X(ejω)采样得到X(k)，
X(k)X(ej)|2πk, k0,1, ,5 6
第３章 离散傅里叶变换(DFT)及其快速算法
(FFT)
当然， 截取信号的长度要足够长。 但如果截取的长度 不够长， 而依靠在所截取的序列尾部加零点， 增加变换区 间长度， 也不会提高分辨率。 例如， 分析周期序列的频谱， 只观察了一个周期的1/4长度， 用这些数据进行DFT， 再通 过尾部增加零点， 加大DFT的变换区间N， 也不能分辨出是 周期序列， 更不能得到周期序列的精确频率。
令m=N－1－n， 则上式可写成
0
N1
X(k) x(m )W N k(n1) x(m )W N km
m N1
m 0
W N k(N 1 )X ( (k)N )R N (k)
第３章 离散傅里叶变换(DFT)及其快速算法
(FFT)
当 k N 时（N为偶数）， 2
因为
X N 2 W N N 2(N 1 )X N 2 NW N N 2(N 1 )X N 2

数字信号处理第三章习题答案

数字信号处理第三章习题答案
1 最小记录时间 ; 2 最大取样间隔 ； 3 最少采样点数 ； （4）在频带宽度不变的情况下, 将频率分辨率提高一倍的N值。
解 （1） 已知F＝50Hz （2） （3）
（4）频带宽度不变就意味着采样间隔T不变, 应该使记录时间 扩大一倍为0.04s实现频率分辨率提高1倍（F变为原来的1/2）.
解
、
和
(a)、(b)、(c)所示。
分别如题3解图
x1(n) (a)
x2(n) (b)
y (n)
(a)
(b)
(c) (c)
5.如果X(k)=DFT[ x(n)], 证明DFT的初值定 理 证明 由IDFT定义式
可知
14.两个有限长序列x(n)和y(n)的零值区间为 x(n)=0, n<0, 8≤n y(n)=0, n<0, 20 ≤ n
对每个序列作20点DFT, 即
X (k)=DFT [x(n)],
Y(k)=DFT [y(n)],
如果
F(k)=X(k)▪Y(k),
k=0,1,…,19 k=0,1,…,19 k=0,1,…,19
f(n)=IDFT [F(k)], k=0,1,…,19
试问在哪些点上f(n)=x(n)*y(n)?为什么？
解 如前所述, 记
,而
fl(n)长度为27,f(n)长度为20.前面已推出二者的关系为
只有在如上周期延拓序列中无混叠的点上, 才满足f(n)=fl(n)7
21-47
41-67
1-7
21-27
8-20
7-19 当从0开始时候
15.用微处理器对实数序列作谱分析, 要求谱分辨率F≤50Hz, 信号最高频率为1kHz, 试确定以下各参数；
教材第三章习题解答

数字信号处理原理与实践方勇习题答案。三章全

数字信号处理原理与实践方勇习题答案。三章全

第一章习 题1-1 有一个连续信号)2cos()(ψπ+=ft t x a ，式中Hz f 20=，2πψ=，（１） 求出)(t x a 的周期；（２） 用采样间隔s T 02.0=对)(t x a 进行采样，写出采样信号)(ˆt xa 的表达式； （３） 画出对应)(ˆt xa 的时域离散信号（序列）)(n x 的波形，并求出)(n x 的周期。

解：（1）)(t x a 的周期是（2）∑∞-∞=-+=n a nT t fnT t x)()2cos()(ˆδψπ（3）)(n x 的数字频率为πω8.0=，252=ωπ周期5=N 。

)28.0cos()(ππ+=n n x ，画出其波形如题1-1图所示。

题1-1图 1-2 设)sin()(t t x a π=，()()sin()a s s x n x nT nT π==，其中s T 为采样周期。

（1）)(t x a 信号的模拟频率Ω为多少？ （2）Ω和ω的关系是什么？（3）当s T s 5.0=时，)(n x 的数字频率ω为多少？ 解：（1）)(t x a 的模拟频率s rad /π=Ω。

（2）Ω和ω的关系是：s T ⋅Ω=ω。

（3）当s T s 5.0=时，rad πω5.0=。

1-3 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）)873cos()(ππ-=n A n x ，A 为常数；（2）)81()(π-=n j e n x 。

解： （1）πω73=，3142=ωπ，这是有理数，因此是周期序列，周期是14=T ； （2）81=ω，πωπ162=，这是无理数，因此是非周期序列。

1-4 研究一个线性时不变系统，其单位脉冲响应为指数序列)()(n u a n h n =，10<<a 。

对于矩阵输入序列，求出输出序列，并用MA TLAB 计算，比较其结果。

分析：输入)()(n R n x N =，线性时不变系统的输出等于输入序列与单位脉冲响应的卷积，用公式表示为∑∞-∞=-⋅=*=k k n h k x n h n x n y )()()()()(为了计算输出序列的第n 个值，必须计算出乘积)()(k n h k x -⋅，并将所得到的序列值相加。

第三章习题答案1要点

第三章习题答案1要点

第三章习题答案1要点数字信号处理学习拓展3－1 画出H(z)?解：(2?0.379z?1)(4?1.24z?1?5.264z?2)(1?0.25z)(1?z?1?1?0.5z)?2级联型网络结构。

x(n)z?10.2524y(n)z?1-1.24-0.5-0.379z?15.264(2?3z?1)(4?6z?1?5z?2)3－2 画出H(z)?级联型网络结构。

?1?1?2(1?7z)(1?z?8z)解： x(n)24y(n)z?17?3z?1?6?8z?15523?z?1?z?2333－3 已知某三阶数字滤波器的系统函数为H(z)?，试画出其1?11?11?2(1?z)(1?z?z)322并联型网络结构。

解：将系统函数H(z)表达为实系数一阶，二阶子系统之和，即：21?z?1?H(z)? 1?11?11?21?z1?z?z322由上式可以画出并联型结构如题3-3图所示：3－1数字信号处理学习拓展2x(n)1/31z?1y(n)?1/2?1/2z?1z?11题3-3图3－4 已知一FIR滤波器的系统函数为H(z)?(1?0.7z?1?0.5z?2)(1?2z?1)，画出该FIR滤波器的线性相位结构。

解：因为H(z)?(1?0.7z?1?0.5z?2)(1?2z?1)?1?1.3z?1?0.9z?2?z?3，所以由第二类线性相位结构画出该滤波器的线性相位结构，如题3-4图所示：x(n)1z?1z?1z?1y(n)11.3?0.9题3-4图3－5 已知一个FIR系统的转移函数为：H(z)?1?1.25z?1?2.75z?2?2.75z?3?1.23z?4?z?5求用级联形式实现的结构流图并用MATLAB画出其零点分布及其频率响应曲线。

解：由转移函数可知，N?6，且h(n)偶对称，故为线性相位系统，共有5个零点，为5阶系统，因而必存在一个一阶系统，即z??1为系统的零点。

而最高阶z的系数为+1，所以z??1为其零点。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

数字信号处理(方勇)第三章习题答案3－1 画出)5.01)(25.01()264.524.14)(379.02()(211211------+--+--=z zz z z z z H 级联型网络结构。

解：23－2 画出112112(23)(465)()(17)(18)z z z H z z z z --------+=--+级联型网络结构。

解：()x n ()y n 243－3 已知某三阶数字滤波器的系统函数为1211252333()111(1)(1)322z z H z z z z -----++=-++，试画出其并联型网络结构。

解：将系统函数()H z 表达为实系数一阶，二阶子系统之和，即：()H z 11122111111322z z z z ----+=+-++ 由上式可以画出并联型结构如题3-3图所示：)题3-3图3－4 已知一FIR 滤波器的系统函数为121()(10.70.5)(12)H z z z z ---=-++，画出该FIR 滤波器的线性相位结构。

解： 因为121123()(10.70.5)(12)1 1.30.9H z zz z z z z ------=-++=+-+，所以由第二类线性相位结构画出该滤波器的线性相位结构，如题3-4图所示：()x n 1-1-1z -题3-4图3－5 已知一个FIR 系统的转移函数为：12345()1 1.25 2.75 2.75 1.23H z z z z z z -----=+--++求用级联形式实现的结构流图并用MATLAB 画出其零点分布及其频率响应曲线。

解： 由转移函数可知，6=N ，且)(n h 偶对称，故为线性相位系统，共有5个零点，为5阶系统，因而必存在一个一阶系统，即1±=z 为系统的零点。

而最高阶5-z 的系数为+1，所以1-=z 为其零点。

)(z H 中包含11-+z 项。

所以：11()()(1)H z H z z -=+。

1()H z 为一四阶子系统，设12341()1H z bz cz bz z ----=++++，代入等式，两边相等求得12341()10.2530.25H z zz z z ----=+-++，得出系统全部零点，如图3-5（b ）所示。

系统流图如题3-5（a ）图所示。

)(n x )(n y 1-z 1-z 1-z题3-5（a ）图MATLAB 程序如下，结果如题3-5（b ）图所示：b=[1 1.25 -2.75 -2.75 1.25 1];a=[1]; figure(1) zplane(b,a);figure(2);OMEGA=-pi:pi/100:pi; H=freqz(b,a,OMEGA);subplot(2,1,1),plot(OMEGA,abs(H));subplot(2,1,2),plot(OMEGA,180/pi*unwrap(angle(H)));题3-5（b ）图3－6 给定26()1(164)H j Ω=+Ω，确定模拟滤波器的系统函数()H s 。

解：根据给定的平方幅度响应，得262311()1641()0.5H j ⨯Ω==Ω+Ω+与221()1()NcHj Ω=Ω+Ω比较，得到3,0.5cN =Ω=。

取左半平面的三个极点，得1262θπππ=+=，极点111(cos sin )c sj θθ=Ω+； 222θπππ=+=，极点222(cos sin )c csj θθ=Ω+=-Ω；因此由()()N ck kH s s s Ω=-∏，得3123()()()()cH s s s s s s s Ω=---对共轭极点1s ，3s 有2213111()()()()2cos c cs s s s s s s s s s θ*--=--=-Ω+Ω代入上式，得20.125()(0.5)(0.50.25)H s s s s =+++3－7 模拟低通滤波器的参数如下：3dBpα=，25dB s α=，25Hz p f =，50Hz s f =，用巴特沃斯近似求()H s 。

解：已知3dBpα=，25dB sα=，25Hz p f =，50Hzs f =，确定巴特沃斯滤波器的阶数如下：250))225s p N ππΩ⨯≥=Ω⨯50lg() 4.1525==取5N =。

本题由于pα正好是3dB ，故低通滤波器的3dB 截止频率为：222550157()c p p f rad s πππΩ=Ω==⨯==或者，由下式来求取cΩ。

110.10.13210225157()(101)(101)ppc Nrad s απ⨯Ω⨯Ω===--将cΩ代入五阶巴特沃斯模拟低通传递函数54321()() 3.236() 4.236() 4.236() 3.236()1c c c c cH s s s s s s=+⨯+⨯+⨯+⨯+ΩΩΩΩΩ1159494634211.04810 5.32610 5.32610 1.09510 1.719100.0211s s s s s s -----=⨯+⨯+⨯+⨯+⨯++3－8 已知1()1/acH s s =+Ω，使用脉冲响应不变法和双线性方法分别设计数字低通滤波 器，使得3dB 截止频率为cω=0.25π。

解：（1）双线性变换法：3dB 截止频率为cω=0.25π，20.250.828tan()2c T TπΩ==于是1()1/0.828aH s sT =+∴11112111()()1(2/0.828)[(1)(1)]a z s T z H z H s z z -----=⋅+==+-+=0.292011110.4159z z--+- 参数T 不参与设计（2）脉冲响应不变法：3dB 截止频率为cω=0.25π，20.250.828tan()2c T TπΩ==于是1()1/0.828aH s sT =+0.828/0.828/T s T=+ 因为脉冲响应不变法是由下面的映射完成的：1111l p Tls pez--→+-所以0.828/10.82810.828/0.828/()11T TTTH z e ze z -⋅--⋅-==--3－9 用脉冲响应不变法将()H s 转换为()H z ，采样周期为T0()()mA H s s s =-，其中m 为任意整数解：[]0-11()()()(1)!s nT m Ah t H s e t u t m -==-L01()()()(1)!m s nTm AT h n Th nT n e u n m -==-[]0011111101()()(1)(1)!(1)!1m m m s nT m n m m s T m n AT AT d H z h n n e z z m m dz e z -∞------=⎛⎫===- ⎪---⎝⎭∑L上式递推可得：000111,11(),2,3,(1)s T s T m s T m AT m e zH z AT e z m e z ---⎧=⎪-⎪=⎨⎪=⎪-⎩3－10 要求设计一个数字低通滤波器，在频率低于0.2613ωπ=的范围内，低通幅度特性为常数，并且不低于0.75dB ，在频率0.4018ωπ=和π之间，阻带衰减至少为20dB 。

试求出满足这些指标的最低阶巴特沃斯滤波器的传递函数)(z H ，采用双线性变换。

解：令2()aH j Ω为模拟滤波器的平方幅度函数，且由于采用双线性变换，2tan(/2)TωΩ=若1T =，故我们要求0.261320lg (2tan())0.7520.401820lg (2tan())202a H j Ha j ππ≥-≤-因此巴特沃斯滤波器的形式为：221()1(/)a Na H j Ω=+ΩΩ所以20.075222tan(0.1306)1()102tan(0.2009)1()10NcNcππ+=Ω+=Ω因此：20.0751lg[(101)/(101)]2lg[tan(0.2009)/tan(0.1306)]N ππ--==1lg[99/0.1885]220.136160.36153⨯-+=1 2.72033 6.0352520.22537⨯=指标放松一点，可以取6N =，代入上式得2621/122tan(0.2009)1()102tan(0.2009)990.9967ccc ππ⨯+=Ω=ΩΩ=对于这个0.9967cΩ=值，通带技术指标基本达到，阻带技术指标刚好满足，在s 平面左半部由三个极点对，其坐标为1()2(1)c j NpsΩ=-。

极点对1：0.25790.9627j -±；极点对2：0.70470.7047j -±；极点对3：0.96270.2579j -±。

于是2220.9804()(0.51580.9933)( 1.40940.9933)( 1.92560.9933)a H s s s s s s s =++++++以112(1)/(1)s zz --=-+代入上式，最后可得16120.0044(1)()1 1.09150.8127z H z z z ---+=⨯-+121210.86910.443410.93920.5597z z z z -----+-+3－11 试设计一巴特沃斯数字低通滤波器，设计指标为：在0.3π通带频率范围内，通带幅度波动小于1dB ，在0.5ππ阻带频率范围内，阻带衰减大于12dB 。

解： 由题意可以得出：pω＝ 0.3πrad , pα＝1dBsω＝ 0.5πrad , sα＝12dB（1）频率预畸变pΩ＝22p tg T ω ＝π15.02tg T＝ 1.019/T rad/s sΩ＝22s tg T ω ＝π25.02tg T＝ 2/T rad/s（2）确定滤波器阶数：spk ＝1101101.01.0--s pαα ＝1101102.11.0-- ＝ 0.1321spλ＝ps ΩΩ ＝ T T 019.112⨯＝1.9627N ＝ －spspk λlg lg ＝ －9627.1lg 1321.0lg ＝ 3.002 ， 取N＝ 3（3）查表求归一化低通滤波器函数)(p H a ＝122123+++p p p（4）求模拟滤波器系统函数110.10.1261.019 1.2764(101)(101)pNc p T Tα--Ω=Ω-=-=（/rad s ）)(s H a ＝)(p H a csp Ω=|＝3322322cc c cs s s Ω+Ω+Ω+Ω332222.07932*1.27642*1.2764 2.0793s T T s Ts =+++(5) 求系统函数)(z H将112(1)(1)z s T z ---=+代入得：)(z H =1231230.07660.23270.23270.076610.80040.50400.6799z z z z z z ------+++-+-3－12 用双线性变换法设计数字低通滤波器，等效模拟滤波器指标参数如下：输入模拟信号)(t xa的最高频率100H dfz=；选用巴特沃斯滤波器，3dB 截止频率100H cfz=，阻带截止频率150H s f z=，阻带最小衰减sα=20dB。