数字信号处理-答案第三章

第三章 部分习题解答（数字信号处理（第二版），刘顺兰，版权归作者所有，未经许可，不得在互联网传播）3.1如果一台通用计算机的速度为平均每次复乘需100μs ，每次复加需20μs ，今用来计算N=1024点的)]([n x DFT ，问用直接运算需要多少时间，用FFT 运算需要多少时间？ 解： ∑−=====101010,21024,)()(N n nk N M N Wn x k X直接运算所需的总时间为s N N s N T d μμ20)1(1002×−+×=秒分62126201023102410010242=≈××+×=s s s μμFFT 运算所需总时间为 s NM s M N T F μμ201002×+×=s s s 717.02010102410010102421=××+×××=μμ3.2在基-2FFT 算法中，最后一级或开始一级运算的系数10==N p N W W ，即可以不做乘法运算。

问（1）乘法可节省多少次，所占百分比为多少？ 解： 可节省2N 次，所占百分比为 %100log 1%100log 2222×=×N N N N 如 8=N 则为%3.33%10031≈×3.11以20kHz 的采样率对最高频率10kHz 的带限信号()a x t 采样，然后计算)(n x 的1000N =个采样点的DFT ，即210()()N j nk N n X k x n eπ−−==∑，1000N =.（1）试求频谱采样点之间的频率间隔是多少?（2）在()X k 中，200k =对应的模拟频率是多少?（3）在()X k 中，700k =对应的模拟频率是多少?解:（1）频谱采样点之间的频率间隔为:20000201000s f f Hz N Δ=== （2）200k =对应的模拟频率为 20000200400041000s k f f k Hz kHz N ==×== （3）因700k =大于N/2,故其对应的模拟频率为 20000()300600061000s k f f N k Hz kHz N =−=×== 3.12 对一个连续时间信号)(t x α采样1s 得到一个4096个采样点的序列：(1) 若采样后没有发生频谱混叠，)(t x α的最高频率是多少？(2) 若计算采样信号的4096点DFT，DFT 系数之间的频率间隔是多少Hz?(3) 假定我们仅仅对Hz f Hz 300200≤≤频率范围所对应的DFT 采样点感兴趣，若直接用DFT，要计算这些值需要多少次复乘？若用按时间抽取FFT 则需要多少次？ 解：（1）由题意可知：4096s f Hz =，故)(t x α的最高频率/22048h s f f Hz == （2）409614096s f f Hz N Δ=== （3）直接用DFT 计算，所需要的复乘次数为(3002001)1014096413696d M N =−+=×=若用按时间抽取FFT 则需要的复乘次数为10log 204812245762F N M N ==×= 3.17若给定两个实序列)(1n x 、)(2n x ，令：)()()(21n jx n x n g +=，)(kG 为其傅里叶变换，可以利用快速傅里叶变换来实现快速运算，试利用傅里叶变换的性质求出用)(k G 表示的)(1n x 、)(2n x 的离散傅里叶变换)(1k X 、)(2k X 。

第三章离散傅里叶变换及其快速算法习题答案参考3.1 图P3.1所示的序列(xn 是周期为4的周期性序列。

请确定其傅里叶级数的系数(X k。

解:(111*0((((((N N N nk nk nk N N N n n n X k x n W x n W x n W X k X k −−−−−=====−= =−=∑∑∑3.2 (1设(xn 为实周期序列,证明(x n 的傅里叶级数(X k 是共轭对称的,即*((X k X k =− 。

(2证明当(xn 为实偶函数时,(X k 也是实偶函数。

证明:(1 111**((([(]((N nk N n N N nk nkNNn n Xk x n W Xk x n W xn W X−−=−−−==−=−===∑∑∑ k(2因(xn 为实函数,故由(1知有 *((Xk X k =− 或*((X k X k −= 又因(xn 为偶函数,即((x n x n =− ,所以有(111*0((((((N N N nk nk nk N N N n n n X k x n W x n W x n W X k X k −−−−−=====−= =−=∑∑∑3.3 图P3.3所示的是一个实数周期信号(xn 。

利用DFS 的特性及3.2题的结果,不直接计算其傅里叶级数的系数(Xk ,确定以下式子是否正确。

(1,对于所有的k; ((10Xk X k =+ (2((Xk X k =− ,对于所有的k; (3; (00X=(425(jkX k eπ,对所有的k是实函数。

解:(1正确。

因为(x n 一个周期为N =10的周期序列,故(X k 也是一个周期为N=10的周期序列。

(2不正确。

因为(xn 一个实数周期序列,由例3.2中的(1知,(X k 是共轭对称的,即应有*((Xk X = k −,这里(X k 不一定是实数序列。

(3正确。

因为(xn (0n ==在一个周期内正取样值的个数与负取样值的个数相等,所以有 10(0N n Xx −=∑ (4不正确。

第三章答案3．1解： (1):由题设：h (n) =)()(10n h n hy (n)=)1()(-n yn y 则u (n) =h (n) y (n)所以可得最陡下降法解：h (n=1) =h *+(I-2μR )2h (0)- h *其中R =)0()1()1()0(yy yy yy yy R R R = 3223（2）：h *= R1-P =3 =1-（3）：由于R =5225 则可得λ1=1，λ2=5；所以μ的取值范围为：0＜μ＜51当μ=61时迭代公式收敛。

（4）：μ=61时h (n) ＝ 14- + 100132× h (0) － 14-＝14- ＋32--(0) － 14-3．2解：（1）空（2）e (n) = x (n)-y (n)[2μe (n-1)y (n-1)+h (n-1)] = x (n)-u (n)[2μe (n-1)y (n-1)+h (n-1)] 对e (n)进行z 变换： e (Z) = x (z) - 2μZ1-e (Z) - Z1-h (Z)由h (n)=2μe (n-1)u (n-1)+h (n-1) 得 h (Z)=2μZ1-e (Z) + Z1-h (Z)h (Z)=1-11)(Z 2--ZZ e μ 所以：e (Z) = x (Z)-2μZ1-e (Z)- Z1-1-11)(z 2--zz e μH (Z) = 11)1(211---+-ZZ μ 所以零点在单位园上，极点在Z = 1-2μ园上。

（3）：要使H(Z)稳定，则极点在单位园内即： 0121><-μμ且3.3(1)性能曲面函数：[][][]⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡---+=-+=+-=-==+-=-=-=-====-==⎥⎦⎤⎢⎣⎡---==-+=1022202222010222)1([)]()1([)]1()([)([102)]([)()55(2125)]1()([0)]()([10)]([85585)]()1([)]1()([25)]1([25)]([)2cos(2)()2sin()()()()()1()()()()]()([)1([)]()1([)]1()([)([)]()([2)]([)(W W n x E n x n x E n x n x E n x E W W WP RW W n d E n n x n d E n x n d E n d E n x n x E n x n x E n x E n x E n N n d n N n x n W n W n W n x n d n x n d E n X n d E P n x E n x n x E n x n x E n x E n X n X E R WP RW W n d E n T T TTT T ξππξ[]⎥⎦⎤⎢⎣⎡--10)1()()()(2W W n x n d n x n d[]⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+-+=10202585585]855852510W W W W⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+--10)55(212502W W1211020)55(21525)45545(2510w w w w w ++++-++=(2)误差性能曲面matlab 程序： (3)[][][][][])1(*)(*2)1(**2)(*)1(**2)(*)(*2)(*)1(**2)(**2 210112001---+-=∂∂-+-+=∂∂⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂=∇n x n d n x E w n x n X E w w n x n d n x n X E w n X E w w w w w Tξξξξξ (4)⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⎥⎥⎦⎤⎢⎢⎣⎡==---* 2.1029-0.6498 7553.40 0.4422 0.1367-0.1367- 0.4422 7553.402.5 0.77250.7725 2.5 )1()()()(1)-(n x 1)-x)n *x(n)1)-x(n *n) x( )( *11221n x n d n x n d n x pR w(5)[][]91-10 1029.2698.04.7553- 0-10 *)(2min ==⎥⎦⎤⎢⎣⎡-=-=*w p n d E T ξ 3.4[][]2725.3*2*27275.1*2*20.70717071.0 0.7071- 7071.02725.3 7275.1 2.5 .0.77250.7725 2.5 1)-(n x 1)-x(n *x(n)1)-x(n * x(n) )(1120102111021w2==∂∂==∂∂====⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡=λλξλλξV V V V n x E R TT[][][][]4216142)2( 8722242 8722112 )]([ 2)]([)(15..3101021201010101010101022+--++=+-⎥⎦⎤⎢⎣⎡+++=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+=-+=ωωωωωωωωωωωωωωωωωωωωωωωεn d E P R n d E n T ）解：（[][][][]()()()[]6222)5(30014'300113122112'21124 )4(438423287)]([)]([ )3(323296872112872112 210'1''1'0min 2min 2110min 2*2min *1*03131*1*011*2'122'02====⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+=Λ+=⎥⎦⎤⎢⎣⎡=Λ∴--=--=⎥⎦⎤⎢⎣⎡--=-Λ+=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+=+==-=⎥⎦⎤⎢⎣⎡-=-==⇒⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⇒⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡==∂∂∂∂--λλεελλλλλλεεεεωεωωωωωεεv v T T TTv v v v v v R E v v v v v v Rv v n d E P n d E P R ）、（3．6 解：（1）[][]()()[][][][][][][][][]NN N NN NN N N N N N T NN NN N N N N n N N N TT TT T T T n d E n n E n d E E n E n n E n n E n r n x n d n r n x n d E n X n d E P R n n n n x n E n r n x E n x n x E n r n x n r n x E n r n x E n nr E n r E n E n r n E n r n x E n r n x n r n x E n r n x n r n x E E n X n X E R n n n X n d E n n X n X E n n n y n d E n e E n ππππππππππππππππππππππππωωωωωϕωωωωϕϕωωεϕϕϕφωωωωωωεπ212021*********221221211022222242222212212212122124221222212cos -122222222210222sin 2cos ))(5.0(2sin 02cos cos )]([)(2]cos 4[)]([sin 0][sin ][sin )]1(sin )1([cos sin cos 2[)]1()1()(())()()(([)]()([cos cos cos ))]cos((cos E[ )]1(sin sin E[1)]-E[x(n)x(n 1)]-E[r(n)r(n )]1()[()]1()([)]1()([))]1()1())(()([(]))1()1([(E )(sin 2)(sin ))((sin ]r(n))E[(x(n)]))1()1([())]()())(1()1([())]1()1())(()([(]r(n))E[(x(n) ]1)-r(n 1)-x(n r(n)x(n)1)-r(n 1)-x(n r(n)x(n)[])()([1)-r(n 1)-x(n r(n)x(n)X(n) )()()]()([2)(])()([)()](E[d ]))()([()]([)(N 4+++++=⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+++=∴====--=-+-+==⎥⎦⎤⎢⎣⎡++=∴=--=-==+-+-+-=-+-+-+-=+=+⎥⎦⎤⎢⎣⎡=++=+=+⎥⎦⎤⎢⎣⎡-+-+-+--+-++=++++==++==-+=-==[]05.0][1044/1T 14.54/1(4)T )21/(1u 0 : ][021][)cos(2/11/2 0 ]cos cos [R -E ]cos cos [)3())cos()21/(()sin()21(2))cos()21/(()sin()cos(20)sin(2)cos(2)5.0(0)cos(2)5.0( )2(2mse21mse112122122122121212212212122221*222220*2201210101======+<<∴<<+=+=+==------=++=⎪⎩⎪⎨⎧-++-=-+=⇒⎪⎩⎪⎨⎧=+++==++===∇-+=∂∂∂∂∂∂∂∂∂∂R ut M u u u R t u R t R r r r N N NN N N N N N N N N N T λλϕϕλλϕλϕλϕλλϕϕϕϕωϕωωωϕωωϕππππππππππππωεπωεωεωεωε值范围为系统收敛的3.11答案：11)(4)(4.0)()]()([2))(()()]([)(min))(()()()()()()1(22222+-=-+===-=n h n h n h n y n x E n y E n h n x E n n e E n n y n h n x n e ξξ5)(04)(8.0)()(==-=n h n h n dh n d ξ （2）μμμξ4)()2.31())(8.04()())(()()1(48.0)(+-=-+=-∇+=+-=∂∂=∇n h n h u n h n n h n h h hn 数迭代计算公式为：最陡下降法推导加权系（3）求加权系数表达式]10)0([)8.01(10])0([)2()(**--+=--+=h h h R I h n h nn μμ要求1max 0-<<λμ5.204.010<<<<∴μμ即3.12答案：2102][][0)1(1011<<==<<∑=--μλμμ即满足为保证收敛应使k k R tr R tr器的收敛速度相同。

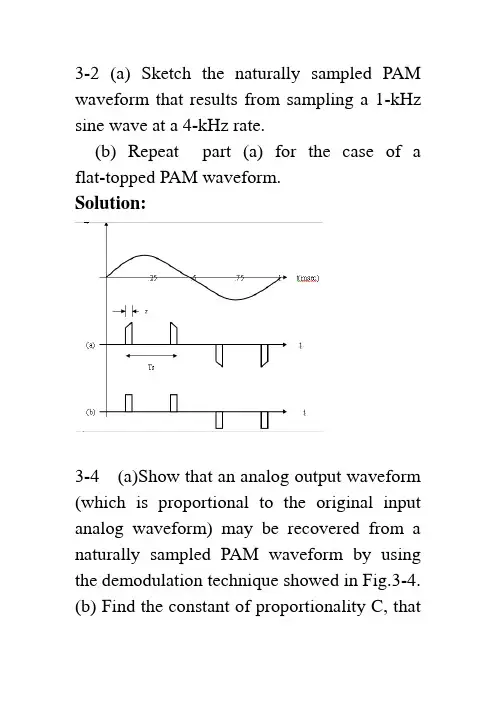
3-2 (a) Sketch the naturally sampled PAM waveform that results from sampling a 1-kHz sine wave at a 4-kHz rate.(b) Repeat part (a) for the case of a flat-topped PAM waveform.Solution:3-4 (a)Show that an analog output waveform (which is proportional to the original input analog waveform) may be recovered from a naturally sampled PAM waveform by using the demodulation technique showed in Fig.3-4.(b) Find the constant of proportionality C, thatis obtained with this demodulation technique , where w(t) is the oriqinal waveform and Cw(t) is the recovered waveform. Note that C is a function of n ,where the oscillator frequency isnfs.Solution:()()()()()()1111sin sin 2cos sin 2cos cos sin [cos 2cos cos sin 2cos s s jk ts k k k jk ts k k s s k s s s s s k n kt kT s t c ek d k d ded d k tk dk dk d w t w t d d k t k d v t w t n tk d w t d n t n d dd k t n tn k ddωωτππωπππωπωππωππωω∞∞-=-∞=-∞∞∞-=-∞=∞=∞=≠-⎡⎤=∏=⎢⎥⎣⎦==+⎡⎤=+⎢⎥⎣⎦==++∑∑∑∑∑∑2]s n t ω211cos cos 222s s n t n tωω=+after LPF:()()()sin sin o w t w t n d d n d n ddn dcw t c ππππ==∴=3-7 In a binary PCM system, if the quantizing noise is not to exceed P ± percent of the peak-to-peak analog level, show that the number of bits in each PCM word needs to be⎪⎭⎫⎝⎛=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛≥P pn 50log 32.350log 10] [log 10102(Hint: Look at Fig. 3-8c.)Solution:Binary PCM M=n2levelsforPPq V P n 100||≤We need)50(log)10(log 50log 5025011002 size step 1022pP n PM P M V P MV nPPPP ≥⎪⎭⎫⎝⎛≥≥=≤≤==δ)(log )(log )(log )(log )(log x b a x x b a b b a ==3-8 The information in an analog voltagewaveform is to be transmitted over a PCM system with a ±0.1% accuracy (full scale). The analog waveform has an absolute bandwidth of 100 Hz and an amplitude range of –10 to +10V .(a) Determine the minimum sampling rate needed.(b) Determine the number of bits needed in each PCM word.(c) Determine the minimum bit rate required in the PCM signal.(d) Determine the minimum absolute channel bandwidth required for transmission of this PCM signal. Solution:(a) Determine the minimum sampling rate needed./sec samples 200)100(22===B f s(b) Determine the number of bits needed in each PCM word.Using the results given in prob. 3-7.(c) Determine the minimum bit rate required in the PCM signal.s f w ords n bits K bits (9)200 1.8 w ord sec sec R ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭(d) Determine the minimum absolute channelbandwidth required for transmission of this920.1%0.1%24250025125009V V V M and n bits a PC M w ord δδδ±=±→====>=→PCM signal.For binary PCM D=RHz9002==⇒D B3-9 An 850-Mbyte hard disk is used to store PCM data. Suppose that a voice-frequency (VF) signal is sampled at 8 ksamples/s and the encoded PCM is to have an average SNR of at least 30dB. How many minutes of VF conversation (i.e., PCM data) can be stored on the hard disk? Solution:53002.6230lg 1022=→=∴=≥=⎪⎭⎫⎝⎛n n M dB MM N S nsec 58sec 40sec 405sec 8kbytes bits byte kbits R kbits sample bits ksamples n f R s =⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⇒=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛==min13,47min 833,2minsec/60sec 10170sec 10170sec10170sec 10510850sec585033336hrs T kbytes Mbytes T ==⨯=⨯=⇒⨯=⨯⨯==3-10 An analog signal with a bandwidth of 4.2 MHz is to be converted into binary PCM and transmitted over a channel, The peak-signal quantizing noise ratio at the receiver output must be at least 55 dB.(a) If we assume that 0=Pe and that there is no ISI, what will be the word length and the number of quantizing steps needed?(b) What will be the equivalent bit rate? (c) What will be the channel null bandwidth required if rectangular pulse shapes are used? Solution:(a) If we assume that 0eP = and that there is no ISI, what will be the word length and the num-ber of quantizing steps needed? Using(3-18),lengthword 9 34.85577.402.6bitsn use n n dB N S peak =⇒≥⇒≥+=⎪⎭⎫⎝⎛steps quantizing 512229===nM(b)sec Mbits6.75Sample bits 9sec 4.8ecMsamples/s4.8)MHz 2.4(22log=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛=====Msamplesn f R f f s anasFor rectangular pulse shapeMHz 6.75==R B null3-12 G iven an audio signal with spectralcomponents in the frequency band 300 to 3000Hz, assume that a sampling rate of 7KHz will be used to generate a PCM signal .Design an appropriate PCM system as follows:a. Draw a block diagram of the PCM system , including the transmitter, channel, receiver.b. S pecify the number of uniform quantization steps needed and the channel null bandwidth required , assume that the peak signal-to-noise ratio at the receiver output needs to be at least 30dB and that polar NRZ signaling is used.c. Discuss how nonuniform quantization canbe used to improve the performance of the system.Solution: (a) 略 (b)lengthword 5 10.43077.402.6bitsn use n n dB N S peak=⇒≥⇒≥+=⎪⎭⎫ ⎝⎛stepsquantizing 32225===nM7sam ples/sec 7 5bits K bits 35 sec Sam ple sec s s f K K sam plesR f n =⎛⎫⎛⎫===⎪⎪⎝⎭⎝⎭()KHzR B null 35==∴( c) uniform quantizing : for all samples,the quantizing noise power is the same 122δ=N↑→↓→NS signal big N S signal smalluniform quantizing is not good for small signal.Nonuniform quantizing: samples are nonlinear processed,Small signal is amplified↑→N S(or small signal ---using small step size ↑→N S )3-14 In a PCM system , the bits error rate dueto channel noise is 10-4. Assume that peak signal-to-noise ratio on the received analog signal needed to be at least 30dB.(a) Find the minimum number of quantizing steps that can be used to encode the analog signal into a PCM signal.(b) If the original analog signal had an absolute bandwidth of 2.7kHz , what is the null bandwidth of PCM signal for the polar NRZ signaling case.Solution: (a) 410-=PedB N S PKout30≥⎪⎭⎫⎝⎛()2231000141PK out S M N M Pe⎛⎫=≥ ⎪+-⎝⎭52206.19===≥n M M use M nKz f s 4.57.22=⨯=27KHz R /274.55＝==⨯==nullsB sKb nf R 3-17 For a 4 bit PCM system , calculate and sketch a plot of the output SNR(in decibels) as a function of the relative input level , ()20lg rmsx V for(a) A PCM system that uses 10μ= law companding(b) A PCM system that uses uniform quantizationWhich of these system is better to use in practice? Why?Solution: n = 4 bits ---- a PCM word (a)()()()6.02 4.7720lg ln 16.024 4.7720lg ln 11021.25dB SNn dBμ=+-+⎡⎤⎣⎦=⨯+-+⎡⎤⎣⎦=(b)() 6.02 4.7720lg ()6.024 4.7720lg ()28.8520lg ()rm s dBrm s rm s S N n x V x V x V =++=⨯++=+3-19 A multilevel digital communication system sends one of 16 possible levels over the channel every 0.8 ms .(a) What is the number of bits corresponding to each level? (b) What is the baud rate? (c) What is the bit rate? Solution:(a) What is the number of bits corresponding to each level?2164/lL l bits level==⇒=(b) What is the baud rate?311,2500.810secN sym bol D baudT -===⨯(c) What is the bit rate?kbits/sec5)250,1(4===lD R3-20 A multilevel digital communication system is to operate at a data rate of 9,600 bits/s.(a) If 4-bit words are encoded into each level for transmission over the channel, what is the minimum required bandwidth for the channel?(b) Repeat part (a) for the case of 8-bit encoding into each level. Solution:(a) If 4-bit words are encoded into each level for transmission over the channel. What is the min-imum required bandwidth for the channel?(b) Repeat part (a) for the case of 8-bit encoding into each level.600600)1200(2121baud 120089600minHz B HzD B D ===≥==3-24 Consider a random data pattern consisting of binary 1’s and 0’s, where the probability of obtaining either a binary 1 or abinary 0 is21. Calculate the PSD for thefollowing types of signaling formats as a function of b T ,the time needed to send 1 bit of data:(a) Polar RZ signaling where the pulse width isbT 21=τ.(b) Manchester RZ signaling where the pulse width isbT 41=τ. What is the first nullbandwidth of these signals? What is the spectral efficiency for each of these signaling cases? Solution:(a) Polar RZ signaling where the pulse width is bT 21=τ.sin(/2)()[()]2/2b b b T fT F f F f t fT ππ==and the data are independent from bit to bit1:1:210,2n n b a AV AV →+→-，依概率依概率()222:01,221,2nn knFor k A a a a and I A +=⎧⎪⎪===⎨⎪-⎪⎩依概率依概率()2222111(0)()22n n i ii R a a P A A A ===⨯+-⨯=∑The first-null bandwidth is RT B bnull 22==andthe bandwidth efficiency is12R B η==(b) Manchester RZ signaling where the pulse width isbT 41=τ. What is the first nullband-width of these signals? What is the spectral efficiency for each of these signaling cases?()()2,0:3400,0A k Thus R k k ⎧==-⎨≠⎩()()22S s2222222()P ()336T sin (/2)12(/2)sin (/2)4(/2)sj k f T k b b b b b b b F f fR k a T fT A T fT A T fT fT eπππππ∞=-∞=-⎛⎫= ⎪⎝⎭=∑Equation (3-36) can also be used to evaluate the PSD for RZ Manchester signaling where the pulse shape is shown in the figure.⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛=-22)sin()(τωτωτπτπτj j ee f f f F⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⇒2sin )sin(2)(ωττπτπτf f j f FUsing (3-40) and (3-36), the PSD forManchester signaling is()()2222)][sin(sin 4)(τπτπτπτf f f T A f p b⎥⎦⎤⎢⎣⎡=IfbT 41=τ, this becomes2224sin 44sin 41)(⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=b b b b fT fT fT T A f p πππThe first-null bandwidth is RT B bnull 44==and thespectral efficiency is41=η(bits/sec)/Hz.3-29 The data stream 01101000101 appears at the input of a differential encoder. Depending on the initial start-up condition of the encoder, find out two possible differential encoded data streams that can appear at the output. Solution:3-30 Create a practical block diagram for a differential encoding system. Explain how thesystem work by showing the encoding and decoding for the sequence 001111010001. Assume that the reference digit is a binary 1. Show that error propagation can not occur. Solution:3-34 The information in an analog waveform is first encoded into binary PCM and then converted to a multilevel signal for transmission over the channel. The number of multilevels is eight. Assume that the analog signa has a bandwidth of 2700Hz and is tobe reproduced at the receiver output with an accuracy of 1%±(full scall).(a) Determine the minimum bit rate of the PCM signal.(b) Determine the minimum baud rate of the multilevel signal.(c) Determine the minimum absolute channel bandwidth required for transmission of this PCM signal. Solution:1221%50624100V M n V V δδδ±=±→=→==→= m in ()62270032.4/()28332.410.83()5.42s la R nf kb s b L L l R D kBdlD c B kH z==⨯⨯=========3-35 A binary waveform of 9600bits/s is converted into an octal (Multilevel) waveform that is pass through a channel with a raisedcosine-rolloff Nyquist filter characteristic . The channel has a conditioned (equalized) phase response out to 2.4kHz .(a) What is the baud rate of the multilevel signal?(b) What is the rolloff factor of the filtercharacteristic?Solution:09600()8332003()(1)(1) 2.40.52R a L l D Bdl D b B f r r kH z r =→=====+=+=→=3-37 A binary communication system uses polar signal. The overall impulse response is designed to be of thesin x xtype, as given byEq(3-67),so that there will be no ISI. The bitrate is 300/s R f bit s ==.(a) What is the baud rate of the polar signal? (b) Plot the waveform of polar signal at the system output when the input binary data is 01100101. Can you discern the data by looking at this polar waveform? Solution:1502s T f B H z==(b)sin ()s e s f t h t f t ππ=1()eSsf H f f f ⎛⎫= ⎪⎝⎭∏1Ss f DT ==3-43 Using the results of prob.3-42, demonstrate that the following filter characteristics do or do not satisfy Nyquist ’s criterion for eliminating ISI (0022s f f T ==).()()00122eT a H f fT ⎛⎫=⎪⎝⎭∏()()00223eT b H f fT ⎛⎫=⎪⎝⎭∏Solution:()()000012222e T T f a H ffT f ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭∏∏()()0000232322eT T f b H f fT f ⎛⎫⎪⎛⎫==⎪⎪⎝⎭⎪⎝⎭∏∏3-45 An analog signal is to be converted into a PCM signal that is a binary polar NRZ line code. The signal is transmitted over a channel that is absolutely bandlimited to 4kHz. Assume that the PCM quantizer has 16 steps and that the overall equivalent system transfer function is of the raised cosine-rolloff type with r =0.5.(a) Find the maximum PCM bit rate that can be supported by this system without introducing ISI.(b) Find the maximum bandwidth that canbe permitted for the analog signal . Solution:()0:164 a PC M w ord 40.522 5.33/1T T M n B kH zr B a R D f kb sr==→=====⨯=+量化器()analog analog 2 5.331000667224s b R nf n B R B H zn=≥⋅⨯∴≤==⨯3-47 Multilevel data with an equivalent bit rate of 2,400 bits/s is sent over a channel using a four-level line code that has a rectangular pulse shape at the output of the transmitter. The overall transmission system (i.e., the transmitter, channel, and receiver) has an r =0.5 raised cosine-rolloff Nyquist filtercharacteristic.(a) Find the baud rate of the received signal.(b) Find the 6-dB bandwidth for this transmission system.(c) Find the absolute bandwidth for the system. Solution:(a) Find the baud rate of the received signal.242=⇒==l L l2400/1200aud2D R l B ===(b) Find the 6-dB bandwidth for thistransmission system.611(1200)600H z 22dB B D ===(c) Find the absolute bandwidth for the system.113(1)(10.5)(1200)(1200)900224absolute T B B r D H z==+=+==3-54 One analog waveform w 1(t ) is bandlimited to 3 kHz, and another, w 2(t), is bandlimited to 9 kHz. These two signals are to be sent by TDM over a PAM-type system. (a) Determine the minimum sampling frequency for each signal, and design a TDM commutator and decommutator to accommodate the signals.(b) Draw some typical waveforms for w 1(t ) and w 2(t ), and sketch the corresponding TDM PAM waveform. Solution:(a) Determine the minimum sampling frequency for each signal, and design a TDM commutator and decommutator to accommodate the signals. TDM1122(): 3kH z 6ksam ples/sec (): 9kH z 18ksam ples/secs s t B f t B f ωω=⇒==⇒=(b) Draw some typical waveforms for w 1(t ) and w 2(t ), and sketch the corresponding TDM PAM waveform.3-56 Twenty-three analog signals , each with a bandwidth of 3.4kHz, are sampled at an 8-kHz rate and multiplexed together with a synchronization channel (8kHz)into a TDM PAM signal. This TDM signal is passed through a channel with an overall raised cosine-rolloff Nyquist filter characteristic of r=0.75.(a) Draw a block diagram for the system, indicating the fc of the commutator and the overall pulse rate of the TDM PAM signal.(b) Evaluate the absolute bandwidth required for the channel.Solution:248k pulses/sec=192k pulses/sec D =⨯()()192k pulse/sec110.75168kH z 22D B r =+=+=3-58 Rework Prob.3-56 for a TDM pulse code modulation system in witch an 8-bit quantizer is used to generate the PCM words for each of the analog inputs and an 8-bit synchronization word is used in the synchronization channel.Solution:3-59 Design a TDM PCM system that will accommodate four 300-bit/s (synchronous) digital inputs and one analog input that has a bandwidth of 500Hz. Assume that the analog samples will be encoded into 4-bit PCM word. Draw a block diagram for your design, analogous to Fig.3-39, indicating the data rates at the various points on the diagram. Explain how your design works.Solution:3-60 Design a TDM PCM system that will accommodate two 2400-bit/s synchronous digital inputs and an analog input that has a bandwidth of 2700 Hz. Assume that the analog input is sampled at 1.11111 times the Nyquist rate and converted into 4-bit PCM word. Draw a block diagram for your design, and indicate the data rates at the various points on your diagram. Explain how your TDM scheme works.Solution:。

数字信号处理刘顺兰第三章完整版习题解答一、题目解答1. 题目利用时域抽样、频域抽样、零填充、插值法等，实现信号的变换。

1.1 时域抽样时域抽样是指将一个连续时间信号在时间轴上的等间隔位置上进行采样，可以得到一个离散时间信号。

时域抽样的原理是，将时间轴上的信号按照一定的时间间隔进行采样，每个采样点的振幅值就是该点对应的连续时间信号的振幅值。

时域抽样可以通过以下步骤进行实现：1.假设连续时间信号为x(t)，采样频率为Fs（采样频率是指每秒采样的次数），采样间隔为Ts（采样间隔是指相邻两个采样点之间的时间间隔）。

2.根据采样频率和采样间隔，计算出采样点数N：N =Fs * T，其中T为采样时长。

为Ts。

4.在每段的中点位置进行采样，得到N个采样点。

5.将N个采样点按照时域顺序排列，即可得到离散时间信号。

1.2 频域抽样频域抽样是指将一个连续频谱信号在频率轴上的等间隔位置上进行采样，可以得到一个离散频谱信号。

频域抽样的原理是，将频率轴上的信号按照一定的频率间隔进行采样，每个采样频率点上的能量值就是该频率点对应的连续频谱信号的能量值。

频域抽样可以通过以下步骤进行实现：1.假设连续频谱信号为X(f)，采样频率为Fs（采样频率是指每秒采样的次数），采样间隔为Δf（采样间隔是指相邻两个采样频率点之间的频率间隔）。

2.根据采样频率和采样间隔，计算出采样点数N：N =Fs / Δf，其中Δf为采样频率点之间的频率间隔。

为Δf。

4.在每段的中点位置进行采样，得到N个采样频率点。

5.将N个采样频率点按照频域顺序排列，即可得到离散频谱信号。

1.3 零填充零填充是指在信号的末尾添加一些零值样本，使得信号的长度变长。

零填充的原理是，通过增加信号的长度，可以在时域和频域上提高信号的分辨率，从而更精确地观察信号的特征。

零填充可以通过以下步骤进行实现：1.假设原始信号为x(n)，长度为N。

2.计算需要填充的长度L，L > 0。

绪论单元测试1.确定性信号和随机信号的区别是什么？A:能否用计算机处理B:能否用有限个参量进行唯一描述答案:B2.如何由连续时间信号获得离散时间信号？A:在时域上对连续时间信号进行采样B:在信号幅度上进行量化答案:A第一章测试1.以下那个说法是正确的？A:在对连续时间信号进行采样得到离散时间信号的过程中，只要实现了等间隔采样，采样间隔T怎样选择都不会影响采样后离散时间信号的频谱特征。

B:在对连续时间信号进行采样得到离散时间信号的过程中，采样间隔T的选择非常关键，如果选择不当，采样后的离散时间信号将存在频域混叠失真现象。

答案:B2.A:B:C:D:答案:D3.A:对B:错答案:A4.下面哪段语句不会报错？A:x = ones(1,4);nh = 0:2;h = (nh+1)* ones(1,3);n=0:5;y=conv(x,h);stem(n,y);B:x = [1 2 3];h = ones(1,5);n=0:7;y=conv(x,h);stem(n,y);C:x = ones(1,5);nh = 0:2;h = (nh+1).* ones(1,3);n=0:6;y=conv(x,h);stem(n,y);答案:C5.A:B:C:D:答案:D6.请问以下哪个说法是正确的？A:连续时间正弦信号采样后不一定为周期序列。

B:连续时间正弦信号采样后一定为周期序列。

答案:A7.A:B:C:D:答案:C8.A:3B:C:8/3D:8答案:D9.A:10B:40C:5D:20答案:A10.A:线性移不变系统B:线性移变系统C:非线性移不变系统D:非线性移变系统答案:C11.A:非线性移变系统B:非线性移不变系统C:线性移不变系统D:线性移变系统答案:D12.A:B:答案:A13.A:B:C:D:答案:B14.A:非因果、非稳定系统B:因果、非稳定系统C:非因果、稳定系统D:因果、稳定系统答案:D15.A:系统是非因果、稳定系统B:系统是因果、稳定系统C:系统是非因果、非稳定系统D:系统是因果、非稳定系统答案:A16.A:b = [1 1];a = [1 0.9 -0.81];x = ones(1,100);y = filter(b,a,x);B:b = [1 1];a = [1 -0.9 0.81];x = ones(1,100);y = filter(b,a,x);答案:B17.A:10msB:150msC:200msD:2ms答案:D18.A:B:C:采样间隔T的取值是不唯一的。

3－1 画出)5.01)(25.01()264.524.14)(379.02()(211211------+--+--=z zz z z z z H 级联型网络结构。

解：243－2 画出112112(23)(465)()(17)(18)z z z H z z z z --------+=--+级联型网络结构。

解：()x n ()y n 243－3 已知某三阶数字滤波器的系统函数为1211252333()111(1)(1)322z z H z z z z -----++=-++，试画出其并联型网络结构。

解：将系统函数()H z 表达为实系数一阶，二阶子系统之和，即：()H z 11122111111322z z z z ----+=+-++ 由上式可以画出并联型结构如题3-3图所示：)题3-3图3－4 已知一FIR 滤波器的系统函数为121()(10.70.5)(12)H z zz z ---=-++，画出该FIR滤波器的线性相位结构。

解： 因为121123()(10.70.5)(12)1 1.30.9H z zz z z z z ------=-++=+-+，所以由第二类线性相位结构画出该滤波器的线性相位结构，如题3-4图所示：()x n 1-1-1z -题3-4图3－5 已知一个FIR 系统的转移函数为：12345()1 1.25 2.75 2.75 1.23H z z z z z z -----=+--++求用级联形式实现的结构流图并用MATLAB 画出其零点分布及其频率响应曲线。

解： 由转移函数可知，6=N ，且)(n h 偶对称，故为线性相位系统，共有5个零点，为5阶系统，因而必存在一个一阶系统，即1±=z 为系统的零点。

而最高阶5-z 的系数为+1，所以1-=z 为其零点。

)(z H 中包含11-+z 项。

所以：11()()(1)H z H z z -=+。

1()H z 为一四阶子系统，设12341()1H z bzcz bz z ----=++++，代入等式，两边相等求得12341()10.2530.25H z zz z z ----=+-++，得出系统全部零点，如图3-5（b ）所示。

第三章习题答案 3.1 （1）非周期（2）N=1 （3）N=10 （4）N=4 （5）N=20 3.2 02s f f ωπ=，1s sf T = （1）0153,2f ωπ==；0.3s T =，05f π= （2）010,25f ωπ==；0.3s T =，0503f =（3）0,0.55f πω==；0.3s T =，013f =（4）03.5,8.75f ωπ==；0.3s T =，0356f =（5） ()()()(){}0.20.210.20.20.20.2(0.2)(0.2)1cos(0.2)()2130.6cos(0.2)() 1.8()0.6()211.80.6()0.6()2110.910.610.6j n j n n n j n j n n nj n j n j j n e e F n u n F e e u n F e u n F e u n ee ππππππωπωπππ-+-----+=+⎡⎤⎡⎤-=-•+-⎢⎥⎣⎦⎣⎦⎡⎤⎡⎤=-•-+-⎣⎦⎣⎦⎛⎫=-+ ⎪++⎝⎭3.3 function [X]=myDTFT(x, n, w)% 计算DTFT% [X]=myDTFT(x, n, w) %X=输出的DTFT 数组 %x=输入的有限长序列 %n=样本位置行向量 %w=频率点位置行向量 X=x*exp(-j*n ’*w)3.4 (1) 7()10.3j j X e eωω-=- （2）20.51()(10.5)10.5j j j j e X e e e ωωωω---=---（3）2()0.80.1610.4j j j e X e e ωωω--=⨯⨯-（4）112210.920.9()(10.9)10.9(10.9)j j j j j j e e X e e e e ωωωωωω-----⨯-⨯=-=---3.5(1) 23456()642246j j j j j j j X e e e e e e e ωωωωωωω------=++++++（2）234567()642246j j j j j j j j X e e e e e e e e ωωωωωωωω-------=+++++++ （3）234567()642246j j j j j j j j X e e e e e e e e ωωωωωωωω-------=+++---- （4）235678()642246j j j j j j j j X e e e e e e e e ωωωωωωωω-------=+++----3.6 00()()11()211j j j A X e ae ae ωωωωω---+⎡⎤=+⎢⎥--⎣⎦3.7 N=5，()5611()11j j j j j j e ee X e e e ωωωωωω----=+--N=25，()252611()11j j j j j j e e eX e e e ωωωωωω----=+-- N=100，()10010111()11j j j j j j e ee X e e e ωωωωωω----=+-- N=5，》n = -5:5; x =ones(1,11); % x(n)k = -500:499; w = (pi/500)*k; % [-pi, pi] X =1/11* x*exp(-j*pi/500*n'*k); % DTFT magX = abs(X); angX = angle(X); realX = real(X); imagX = imag(X); subplot(2,2,1); plot(w/pi,magX); gridxlabel('以pi 为单位的频率'); title('幅度部分'); ylabel('幅值') subplot(2,2,2); plot(w/pi,angX); gridxlabel('以pi 为单位的频率'); title('相位部分'); ylabel('弧度')-1-0.500.5100.51以pi 为单位的频率幅度部分幅值-1-0.500.51-4-2024以pi 为单位的频率相位部分弧度N=25,>> n = -25:25; x =ones(1,51); % x(n)k = -500:499; w = (pi/500)*k; % [-pi, pi] X =1/51* x*exp(-j*pi/500*n'*k); % DTFT magX = abs(X); angX = angle(X); realX = real(X); imagX = imag(X); subplot(2,2,1); plot(w/pi,magX); gridxlabel('以pi 为单位的频率'); title('幅度部分'); ylabel('幅值') subplot(2,2,2); plot(w/pi,angX); gridxlabel('以pi 为单位的频率'); title('相位部分'); ylabel('弧度')-1-0.8-0.6-0.4-0.200.20.40.60.81以pi 为单位的频率相位部分弧度-1-0.8-0.6-0.4-0.200.20.40.60.81以pi 为单位的频率幅度部分幅值N=100,>> n = -100:100; x =ones(1,201); % x(n)k = -500:499; w = (pi/500)*k; % [-pi, pi] X =1/201* x*exp(-j*pi/500*n'*k); % DTFT magX = abs(X); angX = angle(X); realX = real(X); imagX = imag(X); subplot(2,2,1); plot(w/pi,magX); gridxlabel('以pi 为单位的频率'); title('幅度部分'); ylabel('幅值') subplot(2,2,2); plot(w/pi,angX); gridxlabel('以pi 为单位的频率'); title('相位部分'); ylabel('弧度')-1-0.500.5100.51以pi 为单位的频率幅度部分幅值-1-0.500.51-4-2024以pi 为单位的频率相位部分弧度随着N 的增大，DTFT 的幅度特性主瓣越尖锐，旁瓣越小，越接近于1)(=n x 的DTFT 特性。