当前位置：文档之家 › Eviews6章基本回归模型的OLS估计

Eviews6章基本回归模型的OLS估计

  • 格式：ppt
  • 大小：329.50 KB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

计量经济学-多元线性回归分析;eviews6操作

计量经济学-多元线性回归分析;eviews6操作

E(i ) 0
V(a i)rE (i2)2
C( o i,v j) E (ij) 0
i j i,j 1 ,2 , ,n
假设5，解释变量与随机项不相关
Co(Xvji,i)0
j1,2 ,k
假设6，随机项满足正态分布
i ~N(0,2)
2021/6/4
7
上述假设的矩阵符号表示 式：
假设1，nk矩阵X是非随机的，且X的秩=k，即X满
五、样本容量问题
六、估计实例
2021/6/4
10
一、普通最小二乘估计
对于随机抽取的n组观测值 ( Y i,X j) ii , 1 , 2 , ,n ,j 0 , 1 , 2 , k
如果样本函数的参数估计值已经得到，则有：
Y ˆ i ˆ 1 ˆ 2 X 2 i ˆ 3 X 3 i ˆ k X kii=1,2…n
1、线性性
β ˆ(X X )1X Y CY
其中,C=(X’X)-1 X’ 为一仅与固定的X有关的行向量
2021/6/4
18
2、无偏性
E(βˆ) E((XX)1 XY) E((XX)1 X(Xβ μ)) β (XX)1 E(Xμ) β
这里利用了假设: E(X’)=0
3、有效性（最小方差性）
习惯上：把常数项看成为一虚变量的系数，该 虚变量的样本观测值始终取1。这样：
模型中解释变量的数目为（k）
2021/6/4
3
模 型 ： Y t 1 2 t X 2 t k X k t u t
也被称为总体回归函数的随机表达形式。它 的
非随机表达式为: E ( Y i | X 2 i , X 3 i , X k ) i 1 2 X 2 i 3 X 3 i k X ki

eviews--回归分析

eviews--回归分析

3、Eviews 的窗口
Eviews 的窗口分为几个部分：标题栏、主菜单栏、命令窗口、状态行和工作区（如图 1-1 所示） 。
1
计量经济软件 Eviews 上机指导及演示示例
图 1-1 Eviews 窗口 （1）标题栏 标题栏位于主窗口的顶部，标记有 Eviews 字样。当 Eviews 窗口处于激活时，标题栏颜 色加深，否则变暗。单击 Eviews 窗口的任意区域将使它处于激活状态。标题栏的右端有三 个按钮：最小化、最大化（或复原）和关闭。标题栏左边是控制框，控制框也有上述三个按 钮的功能且双击它关闭该窗口。 （2）主菜单 主菜单位于标题栏之下。 将指针移至主菜单上的某个项目并用鼠标左键单击， 打开一个 下拉式菜单，通过单击下拉菜单中的项目，就可以对它们进行访问。菜单中黑色的是可执行 的，灰色的是不可执行的无效项目。 主菜单栏上共有 7 个选项： “File”, “Edit”, “Objects”, “View”,“Procs”, “Quick”,“Options”,“Windows”,“Help” 。 （3）命令窗口 主菜单下的区域称作命令窗口。在命令窗口输入命令，按“ENTER”后命令立即执行。 命令窗口中的竖条称为插入点（或提示符） ，它指示键盘输入字符的位置。允许用户在提示 符后通过键盘输入 Eviews（TSP 风格）命令。如果熟悉 Micro TSP(DOS)版的命令，可以直 接在此输入，如同 DOS 版一样使用 Eviews。按 F1 键（或移动箭头） ，输入的历史命令将重 新显示出来，供用户选用。 将插入点移至从前已经执行过的命令行，编辑已经存在的命令，按 ENTER，立即执行原 命令的编辑版本。 命令窗口支持 cut-and-paste 功能，命令窗口、其他 Eviews 文本窗口和其他 Windows 程序窗口间可方便地进行文本的移动。 命令窗口的内容可以直接保存到文本文件中备用， 为 此必须保持命令窗口处于激活状态，并从主菜单上选择“File”→“Save as” 。 若输入的命令超过了命令窗口显示的大小， 窗口中就自动出现滚动条， 通过上下或左右

Eviews6.0第四讲 向量自回归模型

Eviews6.0第四讲 向量自回归模型
7
(4) 在Endogenous Variables和Exogenous Variables编辑 和 编辑 栏中输入相应的内生变量和外生变量。 栏中输入相应的内生变量和外生变量。系统通常会自动给 出常数c作为外生变量，但是相应的编辑栏中输入c作为外 出常数 作为外生变量，但是相应的编辑栏中输入 作为外 作为外生变量 生变量，也可以，因为 只会包含一个常数。 生变量，也可以，因为EViews只会包含一个常数。 只会包含一个常数 其余两个菜单（Cointegration 和 Restrictions）仅与 其余两个菜单（ ） VEC模型有关，将在下面介绍。 模型有关，将在下面介绍。 模型有关
1 s ˆ MSE = ∑( yt +i − yt +i )2 s i=1
(3.2.1)
15
这样可以更正式地用如下的数学语言来描述 Granger因果的定义：如果关于所有的s > 0，基于 t，yt因果的定义：如果关于所有的 因果的定义 ，基于(y 预测y 预测 得到的均方误差，与基于(y 和 1，…)预测 t+s得到的均方误差，与基于 t，yt-1，…)和(xt， xt-1，…)两者得到的 t+s 的均方误差相同 ， 则 y不是由 两者得到的y 不是由x 两者得到的 不是由 Granger引起的。对于线性函数，若有 引起的。对于线性函数， 引起的
ˆ (3.2.2) MSE[E( yt +s | yt , yt −1,⋯ )] ˆ = MSE[E( yt +s | yt , yt −1,⋯, xt , xt −1,⋯ )]
可 以 得 出 结 论 ： x 不 能 Granger 引 起 y。 等 价 的 ， 如 果 。 对于y是外生的 (3.2.2)式成立 ， 则 称 x对于 是外生的 。 这个意思相同的 式成立， 对于 是外生的。 式成立 第三种表达方式是x关于未来的 无线性影响信息 第三种表达方式是 关于未来的y无线性影响信息。 关于未来的 无线性影响信息。

Eviews6.0线性回归

Eviews6.0线性回归
（10）. F统计量和边际显著性水平 F统计量检验回归中所有的系数是否为零(除了常数或截距)。 对于普通最小二乘模型，F统计量由下式计算：
R2 k1
F1R2Tk
在原假设为误差正态分布下，统计量服从 F(k – 1 , T – k) 分布。
25
F统计量下的P值，即Prob(F-statistic), 是F检验的边际显 著性水平。如果P值小于所检验的边际显著水平，比如说 0.05，则拒绝所有系数都为零的原假设。注意F检验是一个 联合检验，即使所有的t统计量都是不显著的，F统计量也可 能是高度显著的。
变量名下；如果是使用公式法来说明方程，EViews会列出实际 系数 c(1), c(2), c(3) 等等。
对于所考虑的简单线性模型，系数是在其他变量保持不变
的情况下自变量对因变量的边际收益。系数 c 是回归中的常数 或者截距---它是当其他所有自变量都为零时预测的基本水平。 其他系数可以理解为假设所有其它变量都不变，相应的自变量
ARCH方法。 EViews计算R2 的公式为：
R21 uˆuˆ
， uˆyXb
(yy)(yy)
其中，uˆ是残差，y 是因变量的均值。
19
（2） R2 调整 使用R2 作为衡量工具存在的一个问题，即在增加新的自变 量时R2 不会减少。在极端的情况下，如果把样本观测值都作R 2为 自变量，总能得到R2 为1。
s uˆuˆ/(Tk)
（4）残差平方和 残差平方和可以用于很多统计计算中，为了方便，现在将 它单独列出：
T
uˆuˆ (yt Xtb)2 t1 21
（5） 对数似然函数值 EViews可以作出根据系数的估计值得到的对数似然函数 值（假设误差为正态分布）。似然比检验可通过观察方程严 格形式和不严格形式的对数似然值之间的差异来进行。 对数似然计算如下：

Eviews数据统计与分析教程章基本回归模型的OLS估计普通最小二乘法

Eviews数据统计与分析教程章基本回归模型的OLS估计普通最小二乘法

EViews统计分析基础教程
三、 多元线性回归模型
通常情况下，把多元线性回归方程中的常数项看作虚拟 变量的系数，在参数估计过程中该常数项始终取值为1。 因而模型的解释变量个数为k+1.多元回归模型的矩阵形 式为
Y = X + u 其中，Y是因变量观测值的T维列向量；X是所有自变量 （包括虚拟变量）的T个样本点观测值组成的T×（k+1） 的矩阵；是k+1维系数向量；u是T维扰动项向量。
EViews统计分析基础教程
五、 线性回归模型的检验
3.异方差性检验
（1）图示检验法
图示检验法通过散点图来判断用OLS方法估计的模 型异方差性，这种方法较为直观。通常是先将回归 模型的残差序列和因变量一起绘制一个散点图，进 而判断是否存在相关性，如果两个序列的相关性存 在，则该模型存在异方差性。
EViews统计分析基础教程
EViews统计分析基础教程
五、 线性回归模型的检验
4.序列相关检验
（1）杜宾（D .W .—Durbin-Watson）检验法
如果，
0 < D .W . < dt ，存在一阶正自相关 dt < D .W . < du ，不能确定是否存在自相关 du < D .W . < 4－du ，不存在自相关 4－du < D .W . < 4－dt 不能确定是否存在自相关 4－dt < D .W . < 4 ，存在一阶负自相关
EViews统计分析基础教程
五、 线性回归模型的检验
1.拟合优度检验
拟合优度检验用来验证回归模型对样本观测值（实
际值）的拟合程度，可通过R2统计量来检验。
EViews统计分析基础教程

Eviews5章基本回归模型的OLS估计PPT课件

Eviews5章基本回归模型的OLS估计PPT课件
White检验的统计量服从χ2分布，即
N· R 2 ～χ2 (k) 其中，N为样本容量，k为自由度，k等于辅助回归模型（）
中解释变量的个数。如果χ2值大于给点显著性水平下对应 的临界值，则可以拒绝原假设，即存在异方差；反之，接 受原假设，即不存在异方差。
28
EViews统计分析基础教程
五、 线性回归模型的检验
“Scatter”选项，生成散点图，进而可判断机
项是否存在异方差性。
26
EViews统计分析基础教程
五、 线性回归模型的检验
3.异方差性检验
（2）怀特（White）检验法 检验步骤：
用OLS（最小二乘法）估计回归方程，得到残差e。
作辅助回归模型：
求辅助回归模型的拟合优度R2的值。
White检验的统计量服从χ2分布，即
25
EViews统计分析基础教程
五、 线性回归模型的检验
3.异方差性检验
（1）图示检验法 检验步骤：
建立方程对象进行模型的OLS（最小二乘）估计，
此时产生的残差保存在主窗口界面的序列对象resid
中。
建立一个新的序列对象，并将残差序列中的数据
复制到新建立的对象中。
然后选择主窗口中的“Quick” | “Graph” |
21
EViews统计分析基础教程
五、 线性回归模型的检验
2.显著性检验
变量显著性检验（t检验）
检验中的原假设为：
备择假设为：
H0：i= 0，
H1：i ≠ 0，
如果原假设成立，表明解释变量x对被解释变量y没
有显著的影响；当原假设不成立时，表明解释变量
x对被解释变量y有显著的影响，此时接受备择假设。
22

EViews软件应用及对OLS的回归分析[研究材料]

EViews软件应用及对OLS的回归分析[研究材料]
引入了流行的对象概念，操作灵活简便，可采用多种操作
方式进行各种计量分析和统计分析，数据管理简单方便。
调研学习
5
EViews 的发展历史
EViews是TSP (Time Series Processor) 软件包的 Windows版本
• 1981年Micro TSP面世，基于DOS操作系统
• 1994年QMS (Quantitative Micro Software) 公司 在Micro TSP基础上开发EViews并投入使用
调研学习
3
A. 什么是EViews
EViews：Econometrics Views， 通常称为计量经济学软
件包。它的本意是对社会经济关系与经济活动的数量规律， 采用计量经济学方法与技术进行“观察” 经济学家开发，主要用于经济学领域，主要处理但不局限 于时间序列数据 当今世界上使用最为广泛的经济计量统计软件之一 在系统数据分析和评价、金融分析、宏观经济预测、模拟、 销售预测、成本分析甚至医学研究等领域中有着广泛的应 用：■ 应用经济计量学 ■ 总体经济的研究和预测 ■ 销售预测 ■ 财务分析 ■ 成本分析和预测 ■ 蒙地卡罗模拟 ■ 经济模型的估计和仿真 ■ 利率与外汇预测
EViews的大多数工作通过工作文件来实现 使用EViews工作的第一步：建立一个新的
工作文件（file/ new/ workfile）或调用一个 已有的工作文件（ file/ open/ EViews workfile ）
调研学习
11
建立一个新工作文件
打开一个已有工作文件
调研学习
12
创建工作文件：File→new→workfile…
1. 工作文件（Workfile） 2. 对象（Object）

实验一 回归模型的OLS估计

实验一 回归模型的OLS估计

实验一回归模型的OLS估计【实验目的】掌握一元线性、非线性回归模型的建模方法【实验内容】建立我国税收预测模型【实验步骤】【例1】建立我国税收预测模型。

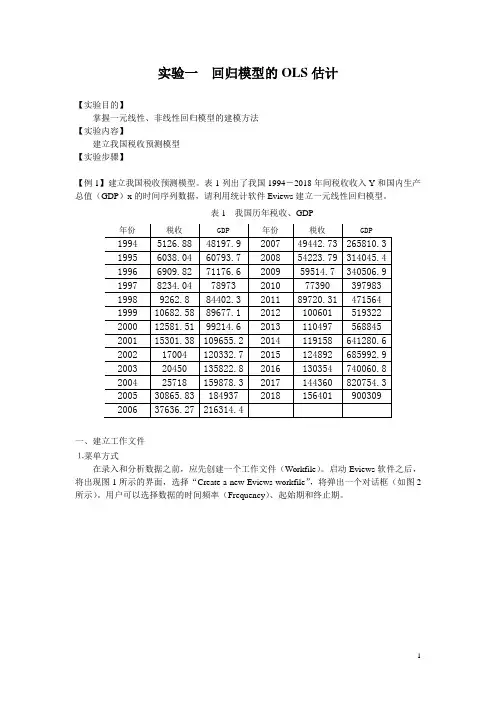
表1列出了我国1994－2018年间税收收入Y和国内生产总值（GDP）x的时间序列数据，请利用统计软件Eviews建立一元线性回归模型。

表1 我国历年税收、GDP一、建立工作文件⒈菜单方式在录入和分析数据之前，应先创建一个工作文件（Workfile）。

启动Eviews软件之后，将出现图1所示的界面，选择“Create a new Eviews workfile”，将弹出一个对话框（如图2所示）。

用户可以选择数据的时间频率（Frequency）、起始期和终止期。

图1 Eviews菜单方式创建工作文件示意图图2 工作文件定义对话框本例中选择时间频率为Annual（年度数据），在起始栏和终止栏分别输入相应的日期94和18。

然后点击OK，在Eviews软件的主显示窗口将显示相应的工作文件窗口（如图3所示）。

图3 Eviews工作文件窗口一个新建的工作文件窗口内只有2个对象(Object）,分别为c（系数向量）和resid（残差）。

它们当前的取值分别是0和NA（空值）。

可以通过鼠标左键双击对象名打开该对象查看其数据，也可以用相同的方法查看工作文件窗口中其它对象的数值。

⒉命令方式还可以用输入命令的方式建立工作文件。

在Eviews软件的命令窗口中直接键入CREATE命令，其格式为：CREATE 时间频率类型起始期终止期本例应为：CREATE A 1994 2018二、输入数据在Eviews软件的命令窗口中键入数据输入/编辑命令：DA TA Y X此时将显示一个数组窗口（如图4所示），即可以输入每个变量的数值图4 Eviews数组窗口三、图形分析借助图形分析可以直观地观察经济变量的变动规律和相关关系，以便合理地确定模型的数学形式。

⒈趋势图分析命令格式：PLOT 变量1 变量2 ……变量K作用：⑴分析经济变量的发展变化趋势⑵观察是否存在异常值本例为：PLOT Y X⒉相关图分析命令格式：SCAT 变量1 变量2作用：⑴观察变量之间的相关程度⑵观察变量之间的相关类型，即为线性相关还是曲线相关，曲线相关时大致是哪种类型的曲线说明：⑴SCAT命令中，第一个变量为横轴变量，一般取为解释变量；第二个变量为纵轴变量，一般取为被解释变量⑵SCAT命令每次只能显示两个变量之间的相关图，若模型中含有多个解释变量，可以逐个进行分析⑶通过改变图形的类型，可以将趋势图转变为相关图本例为：SCA T Y X图5 税收与GDP趋势图图5、图6分别是我国税收与GDP时间序列趋势图和相关图分析结果。

EViews软件应用及对OLS的回归分析ppt课件

EViews软件应用及对OLS的回归分析ppt课件
最新版整理ppt
10
1、工作文件（Workfile）
EViews的大多数工作通过工作文件来实现 使用EViews工作的第一步：建立一个新的
工作文件（file/ new/ workfile）或调用一个 已有的工作文件（ file/ open/ EViews workfile ）
最新版整理ppt
11
最新版整理ppt
47
可以用EViews工作文件窗口菜单上的“View”或对象窗口 工具栏上的“View”来改变对象的视图。一个对象视图的变化并 不改变对象中的数据，仅仅是显示形式改变了。
• 线性坐标视图 最新版整理ppt • line
48
• 柱状坐标视图 • bar
最新版整理ppt
49
有关对象的其他简单的统计分析和相关操作
9
C. EViews应用中的一些基本概念
1. 工作文件（Workfile） 2. 对象（Object）
• EViews的核心是对象，对象是指有一定关系的 信息或算子捆绑在一起供使用的单元，用 EViews工作就是使用不同的对象。
• 对象都放置在对象集合中，其中工作文件 （workfile）是最重要的对象集合。
模型 合成数据
行向量 样本 标量 序列 最新版整理ppt 状态空间
对称矩阵 系统
表格 文本
值图 向量自回归
列向量30
（1）对象的显示限制
当工作文件中包含很多对象时，工作文件窗 口就会显得很乱。可以用显示限制（Filter）来限 制窗口中所显示的对象。对象类型和对象名称可 作为限制条件。
最新版整理ppt
最新版整理ppt
4
A. 什么是EViews
具有现代Windows软件可视化操作的优良性。可以使用鼠

计量经济学 讲义一 EVIEWS6.0

计量经济学 讲义一 EVIEWS6.0

讲义一一．运用Eviews5.0进行一元线性回归的步骤：1．建立工作文件(研究消费与收入的关系)启动Eviews4.exe后，在弹出的窗口中点击“OK”。

点击File\New\Workfile ，在弹出的对话框中选择数据的时间频率（frequency）为Unstructure/Undated (截面数据) ，Data range （以只有10个观测值的一元线性模型为例）为10，点击OK即可。

2．输入数据在主菜单点击Quick\Empty Group ，录入收入（X）、消费（Y）的数据，在窗口中点击数据，就可以修改数据列的名称，点“OK”关闭即可。

在group窗口中点transpose可以改变数据的排列方式。

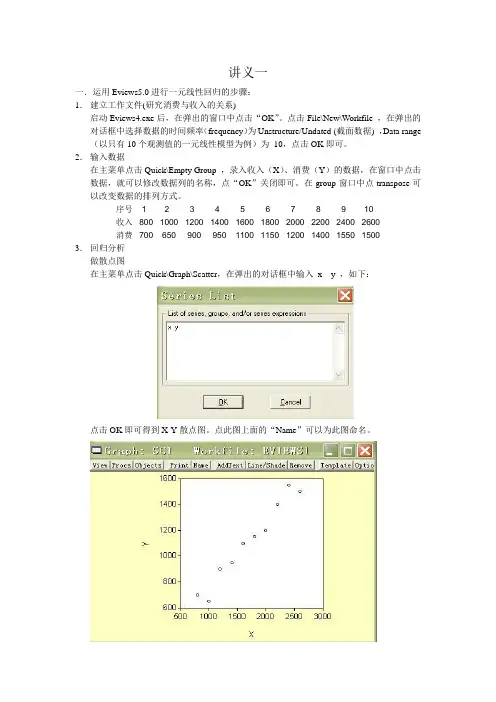
序号 1 2 3 4 5 6 7 8 9 10收入800 1000 1200 1400 1600 1800 2000 2200 2400 2600消费700 650 900 950 1100 1150 1200 1400 1550 15003．回归分析做散点图在主菜单点击Quick\Graph\Scatter，在弹出的对话框中输入x y ，如下：点击OK即可得到X-Y散点图。

点此图上面的“Name”可以为此图命名。

由上面的散点图可以看出，x y存在近似的线性关系。

①OLS估计在主菜单点击Quick\Estimate Equation ，弹出如下对话框：图2 OLS回归分析的设置按图2设置。

输入的顺序为“被解释变量常数项解释变量1 解释变量2”，每个变量之间以空格分开(如果是多元回归就在后面依次添加其他的解释变量即可)。

点击“OK”后，得到如下结果，单击“name”为其命名后就可以关闭。

（同时也可以点击“Freeze”将其保存为表格形式。

而且，此表格不会受到以后操作的影响。

）图3 OLS计算结果其中，最上面的说明分别是“Dependent variable：Y”为“被解释变量是Y”；“Method:Least Squares”为“使用的方法：最小二乘法”；日期（Date）、时间（Time）；样本范围（Sample:1~10）；包含的观测对象（Included observations:10）10个。

eviews基本回归模型

eviews基本回归模型
量更为一般的序列相关检验方法。
2019/1/15 21
7. 因变量均值和标准差（Mean/S.D. dependent var） y 的均值和标准差由下面标准公式算出：
y yi T
i 1
T
sy
y
T t 1
i
y
2
T 1
作为一个规则，如果 DW 值接近 2 ，证明不存在序列相关。 在例 1 的结果中， DW 值很小，表明残差中存在序列相关。关 于 Durbin-Watson 统计量和残差序列相关更详细的内容参见 “序列相关理论”。 对于序列相关还有更好的检验方法。在 “序列相关的检
验”中，我们讨论Q统计量和 LM检验，这些都是比DW统计
2019/1/15
3
§ 6.2 在EViews中对方程进行说明 当创建一个方程对象时，会出现如下对话框：
在这个对话框中需要说明三件事：方程说明，估计方法，估 计使用的样本。在最上面的编辑框中，可以说明方程：因变量 （左边）和自变量（右边）以及函数形式。 有两种说明方程的基本方法：列表法和公式法。列表法简单 但是只能用于不严格的线性说明；公式法更为一般，可用于说明 非线性模型或带有参数约束的模型。
2019/1/15 16
6.4.2 方程统计量
1. R2 统计量(R-squared)
R2 统计量衡量在样本内预测因变量值的回归是否成功。R2
是自变量所解释的因变量的方差。如果回归完全符合，统计值 会等于 1。如果结果不比因变量的均值好，统计值会等于 0。 R2 可能会由于一些原因成为负值。例如，回归没有截距或常数， 或回归包含系数约束，或估计方法采用二阶段最小二乘法或
ARCH方法。
EViews计算R2 的公式为： ˆ u ˆ u 2 R 1 ( y y )( y y ) ，

eviews简单回归方程的构建命令

eviews简单回归方程的构建命令

eviews简单回归方程的构建命令在eviews中，构建简单回归方程的命令为OLS（Ordinary Least Squares）。

该命令用于估计线性回归模型的参数，并进行模型诊断和预测分析。

下面将分步介绍如何使用OLS命令构建简单回归方程。

打开eviews软件，并加载需要进行回归分析的数据集。

点击“File”菜单中的“Open”选项，选择数据文件并加载进入eviews。

确保数据集中包含自变量和因变量的观测值。

接下来，点击“Quick”菜单中的“Estimate Equation”选项。

在弹出的对话框中，选择“Single Equation”并点击“OK”。

在弹出的“Single Equation Estimation”对话框中，选择需要建立回归方程的变量。

将因变量拖放到“Dependent”框中，将自变量拖放到“Independent”框中。

确认变量的顺序和选择是否正确。

然后，在“Estimation Method”选项中选择“Ordinary Least Squares”作为估计方法。

这是最常用的回归分析方法，用于估计线性回归模型的参数。

接下来，点击“OK”按钮进行回归分析。

eviews将根据所选的变量和估计方法，对数据进行回归分析，并生成回归结果报告。

在回归结果报告中，可以查看回归方程的参数估计值、显著性水平、拟合优度等统计指标。

此外，还可以进行残差分析、预测分析等进一步的数据处理和分析。

在进行回归分析后，可以进一步对回归方程进行诊断和验证。

例如，可以检查回归残差的正态性、异方差性等假设。

可以使用eviews 提供的工具和命令进行这些分析。

除了使用OLS命令进行简单回归分析外，eviews还提供了其他回归分析方法和模型。

例如，可以使用最小二乘法进行非线性回归分析，或者使用面板数据模型进行多变量回归分析。

使用eviews进行简单回归方程的构建非常简单。

只需要几个简单的步骤，就可以对数据进行回归分析，并得到相应的回归结果。

Eviews_基本回归模型

Eviews_基本回归模型
量更为一般的序列相关检验方法。
21
7. 因变量均值和标准差（S.D） y 的均值和标准差由下面标准公式算出：
y yi T
i 1
T
sy
y
T t 1
i
y
2
T 1
8. AIC准则(Akaike Information Criterion)
16
§3.4.2 方程统计量
1. R2 统计量 R2 统计量衡量在样本内预测因变量值的回归是否成功。R2 是自变量所解释的因变量的方差。如果回归完全符合，统计值 会等于 1。如果结果不比因变量的均值好，统计值会等于 0。 R2 可能会由于一些原因成为负值。例如，回归没有截距或常数， 或回归包含系数约束，或估计方法采用二阶段最小二乘法或 ARCH方法。 EViews计算R2 的公式为：
R2 调整后的记为 R 2 ，消除R2 中对模型没有解释力的新增
变量。计算方法如下：
T 1 R 1 1 R T k
2

2

R 2从不会大于R2 ，随着增加变量会减小，而且对于很不
适合的模型还可能是负值。
18
3. 回归标准差 (S.E. of regression)
回归标准差是在残差的方差的估计值基础之上的一个总结。 计算方法如下：
2
§3.1 创建方程对象
EViews中的单方程回归估计是用方程对象来完成 的。为了创建一个方程对象: 从主菜单选择Object/New
Object/Equation 或 Quick/Estimation Equation …，或
者在命令窗口中输入关键词equation。 在随后出现的方程说明对话框中说明要建立的方
第三章
基本回归模型

Eviews5章基本回归模型的OLS估计

Eviews5章基本回归模型的OLS估计

编辑课件ppt
5
EViews统计分析基础教程
一、普通最小二乘法（OLS）
2.方程对象
EViews5.1提供了8种估计方法： “LS”为最小二乘法； “TSLS”为两阶段最小二乘法； “GMM”为广义矩法； “ARCH”为自回归条件异方差； “BINARY”为二元选择模型，其中包括Logit模型、 Probit模型和极端值模型； “ORDERED”为有序选择模型； “CENSORED”截取回归模型； “COUNT”为计数模型。
12
EViews统计分析基础教程
四、 线性回归模型的基本假定
线性回归模型必须满足以下几个基本假定：
假定1：随机误差项u具有0均值和同方差，即 E ( ui ) = 0 i=1，2，…，n Var ( ui ) = σ2 i=1，2，…，n
其中，E表示均值，也称为期望，在这里随机误差项u的 均值为0。Var表示随机误差项u的方差，对于每一个样 本点i，即在i=1，2，…，n的每一个数值上，解释变量y 对被解释变量x的条件分布具有相同的方差。当这一假定
样本回归函数为
yt= B1 + B2xt +μt
yt= b1 + b2xt + et 其中，et为残差项，
5-3式为估计方程，b1 和b2分别为B1和B2的估计量， 因而
e = 实际的yt –估计的yt
编辑课件ppt
3
EViews统计分析基础教程
一、普通最小二乘法（OLS）
1.最小二乘原理 估计总体回归函数的最优方法是选择B1和B2的估计量b1 ， b2，使得残差et尽可能达到最小。 用公式表达即为
条直线能反映出该组数据的变化。
如果用不同精度多次观测一个或多个未知量，为了确定各未 知量的可靠值，各观测量必须加改正数，使其各改正数的平 方乘以观测值的权数的总和为最小。因而称最小二乘法。

Eviews数据统计与分析教程6章 基本回归模型的OLS估计-加权最小二乘法

Eviews数据统计与分析教程6章 基本回归模型的OLS估计-加权最小二乘法

EViews统计分析基础教程
Байду номын сангаас
四、非线性最小二乘法（NLS）
基本原理： 设定非线性回归模型的一般式为 yi = f(xi, ,β) + μi i=1，2,…，n 则其残差平方和为
（1）
2 n ˆ S ( ) = y f x , （2） ˆ i i i 1 能使(2)达到最小的为参数β的非线性最小二乘估计。要 得到β的估计值，首先对式（1）中的β求偏导，然后令 该式等于0。 还可以通过迭代法求的近似值，先给出参数估计的初始 值，然后通过迭代法得到一个新的估计值，重复迭代直 到估计值收敛为止。
EViews统计分析基础教程
五、广义矩估计（GMM）
基本原理： 广义矩估计是设定参数满足的一种理论关系。其原理是 选择参数估计尽可能接近理论上关系，把理论关系用样 本近似值代替；并且估计量的选择就是要最小化理论值 和实际值之间的加权距离。参数要满足的理论关系通常 是参数函数f(θ)与工具变量Zt之间的正则条件，即 E[f(θ)′Z]=0，θ是被估计参数 广义矩估计法（GMM）中估计量选择的标准是，使工 具变量与函数f(θ)之间的样本相关性越接近于0越好。
EViews统计分析基础教程
五、广义矩估计（GMM）
EViews基本操作： 选择主菜单栏中 “Object”|“New Object”|“Equation”选项， 或者选择“Quick”|“Estimate Equation” 选项，在 “Method”中选择“GMM”后弹出如下图所示的方程设 定对话框。
基本思路： 赋予每个观测值残差不同的权数，从而使得回归模型的随 机误差项具有同方差性。
EViews统计分析基础教程
一、加权最小二乘法（WLS）

Eviews估计方法汇总

Eviews估计方法汇总

Eviews估计方法汇总来源：计量经济学01最小二乘法（1）普通最小二乘估计（OLS）：这是使用的最为普遍的模型，基本原理就是估计残差平方和最小化，不予赘述。

（2）加权最小二乘估计（WLS）Eviews路径：LS模型设定对话框-----optionsOLS的假设条件最为严格，其他的估计方法往往是在OLS的某些条件无法满足的前提下进行修正处理的。

WLS就是用来修正异方差问题的。

在解释变量的每一个水平上存在一系列的被解释变量值，每一个被解释变量值都有自己的分布和方差。

在同方差性假设下，OLS对每个残差平方ei^2都同等看待，即采取等权重1。

但是，当存在异方差性时，方差δi^2越小，其样本值偏离均值的程度越小，其观测值越应受到重视，即方差越小，在确定回归线时的作用应当越大；反之方差δi^2越大，其样本值偏离均值的程度越大，其在确定回归线时的作用应当越小。

WLS的一个思路就是在拟合存在异方差的模型的回归线时，对不同的δi^2区别对待。

在利用样本估计系数时依旧是使得总体残差最小化，但是WLS会给每个残差平方和一个权重wi=1/δi。

这样，当δi^2越小，wi越大；反之，δi^2越大，wi越小。

Eviews的WLS没有要求权重因子必须是1/δi。

一般纠正异方差性的方法还包括模型变换法，这种方法假定已知Var（ui）=δi^2=δ^2*f(Xi)，令权重wi=f(Xi)^（1/2），用f(Xi)^（1/2）去除原模型，可知随机干扰项转换为ui/f(Xi)^（1/2），这时Var（ui）=δi^2=δ^2，即实现了同方差。

由上面的分析可知，WLS核心就是找到一个等式：Var（ui）=δi^2=δ^2*f(Xi)。

这个等式经过调整更容易理解：δ^2=δi^2/f(Xi)或δ=δi/f(Xi)^（1/2）。

δ为某一常数，权重wi=1/f(Xi)^（1/2），经过wi的加权便实现了同方差。

前面提到的特殊权重wi=1/δi，即f(Xi)=1/δi^2,这时δ=δi/f(Xi)^（1/2）=1。

Eviews统计第六章

Eviews统计第六章


自相关检验及修正的EViews操作


1.绘图检验自相关问题的EViews操作 进行了OLS回归后，选择EViews主窗口的Quick|Graph命令，输入残差序列名 （Resid），选择图形类型，最后单击确定键即得到残差图。绘制残差序列图也可以通 过Equation对象窗口的Resids按钮或View|Acutal,Fitted,Residual命令实现。 2.DW检验操作 通常OLS回归估计输出结果中包含着对模型的D.W.检验结果，无需单独进行操作。通 过查询DW临界值表可以判断模型自相关问题。DW统计量值越接近2，表明自相关程 度越弱。

异方差与加权最小二乘法 3.异方差的常用检验方法
观表现出变量之间的关系。利用时间序列 图、散点图以及残差序列对解释变量的散点图可以直观的 对模型否存在异方差进行初步判断。 （2）怀特检验 怀特检验通过OLS估计求得残差的估计值，然后利用残差 估计值的平方与解释变量及其交叉项辅助回归式，得到拟 合优度 ，从而构建统计量进行检验。 怀特检验的原假设为原回归模型不存在异方差，被择假设 为原回归模型存在异方差。


应用普通最小二乘法时要求模型的随机误差项必须满足：
（1）无偏性假定。即所有随机误差项的期望为0 （2）同方差性假定。即所有随机误差项的方差相等 （3）无序列相关性假定。即随机误差项之间无序列相关性 （4）解释变量与随机误差项相互独立。即解释变量X为非随机变量 （5）正态性假定。即随机误差项服从均值为0的正态分布。



5.异方差形式未知时的模型处理方法-White异方差一致协方差估计 当异方差形式未知时，无法使用加权最小二乘法（Weighted Least Square，WLS）消除异方差，此时需要采用White异方差一致协方差 估计。

Eviews数据统计与分析教程5章 基本回归模型OLS估计-普通最小二乘法

Eviews数据统计与分析教程5章 基本回归模型OLS估计-普通最小二乘法
2.方程对象
选择工作文件窗口工具栏中的“Object”| “New Object”| “Equation”选项，在下图所示的对话框中输入方程变量。
EViews统计分析基础教程
一、普通最小二乘法（OLS）
2.方程对象
EViews5.1提供了8种估计方法： “LS”为最小二乘法； “TSLS”为两阶段最小二乘法； “GMM”为广义矩法； “ARCH”为自回归条件异方差； “BINARY”为二元选择模型，其中包括Logit模型、Probit 模型和极端值模型； “ORDERED”为有序选择模型； “CENSORED”截取回归模型； “COUNT”为计数模型。
五、 线性回归模型的检验
3.异方差性检验
异方差性的后果 ：
当模型出现异方差性时，用OLS（最小二乘估计法）得到的 估计参数将不再有效；变量的显著性检验（t检验）失去意 义；模型不再具有良好的统计性质，并且模型失去了预测 功能。
EViews统计分析基础教程
五、 线性回归模型的检验
4.序列相关检验
方法：
EViews统计分析基础教程
四、 线性回归模型的基本假定
线性回归模型必须满足以下几个基本假定：
假定1：随机误差项u具有0均值和同方差，即 E ( ui ) = 0 i=1，2，…，n Var ( ui ) = σ2 i=1，2，…，n 其中，E表示均值，也称为期望，在这里随机误差项u的 均值为0。Var表示随机误差项u的方差，对于每一个样本 点i，即在i=1，2，…，n的每一个数值上，解释变量y对 被解释变量x的条件分布具有相同的方差。当这一假定条 件不成立是，称该回归模型存在异方差问题。
EViews统计分析基础教程
四、 线性回归模型的基本假定

Eviews数据统计与分析教程5章 基本回归模型的OLS估计-普通最小二乘法

Eviews数据统计与分析教程5章 基本回归模型的OLS估计-普通最小二乘法

EViews统计分析基础教程
五、 线性回归模型的检验
3.异方差性检验 （1）图示检验法 检验步骤：
建立方程对象进行模型的OLS（最小二乘）估计， 此时产生的残差保存在主窗口界面的序列对象 resid中。 建立一个新的序列对象，并将残差序列中的数据 复制到新建立的对象中。 然 后 选 择 主 窗 口 中 的 “ Quick‖ | ―Graph‖ | ―Scatter‖选项，生成散点图，进而可判断随机项 是否存在异方差性。
EViews统计分析基础教程
二、一元线性回归模型
2.实际值、拟合值和残差
估计方程为
表示的是yt的拟合值， 和 分别是 0 和1的估计量。 实际值指的是回归模型中被解释变量（因变量）y的原始观 测数据。拟合值就是通过回归模型计算出来的yt的预测值。
EViews统计分析基础教程
二、一元线性回归模型
EViews统计分析基础教程
一、普通最小二乘法（OLS）
1.最小二乘原理
估计总体回归函数的最优方法是选择B1和B2的估计量b1 ，b2， 使得残差et尽可能达到最小。 用公式表达即为
总之，最小二乘原理就是选择样本回归函数使得y的估计值 与真实值之差的平方和最小。
EViews统计分析基础教程
一、普通最小二乘法（OLS）
EViews统计分析基础教程
五、 线性回归模型的检验
3.异方差性检验
（2）怀特（White）检验法
在EViews5.1软件中选择方程对象工具栏中的“View‖ | ―Residual Tests‖ | ―White Heteroskedasticity‖选项即 可完成操作。
EViews统计分析基础教程
最小二乘原理设双变量的总体回归方程为ytb1b2xtt样本回归函数为样本回归函数为ytb1b2xtet其中et为残差项53式为估计方程b1和b2分别为b1和b2的估计量因而e实际的yt估计的yteviews统计分析基础教程一普通最小二乘法ols1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

EViews统计分析基础教程
四、非线性最小二乘法（NLS）
基本原理： 设定非线性回归模型的一般式为 yi = f(xi, ,β) + μi i=1，2,…，n 则其残差平方和为
（1）
2 n ˆ S ( ) = y f （2） ˆ xi , i i 1 能使(2)达到最小的为参数β的非线性最小二乘估计。要 得到β的估计值，首先对式（1）中的β求偏导，然后令 该式等于0。 还可以通过迭代法求的近似值，先给出参数估计的初始 值，然后通过迭代法得到一个新的估计值，重复迭代直 到估计值收敛为止。
EViews统计分析基础教程
五、广义矩估计（GMM）
EViews基本操作： 选择主菜单栏中 “Object”|“New Object”|“Equation”选项， 或者选择“Quick”|“Estimate Equation” 选项，在 “Method”中选择“GMM”后弹出如下图所示的方程设 定对话框。
EViews统计分析基础教程
本章小结：
• 了解WLS、GLS、NLS、TSLS、GMM五种估计方 法的基本原理 • 掌握这五种估计法的EViews相关操作
EViews统计分析基础教程
一、加权最小二乘法（WLS）
1.异方差问题的解决
消除方法（EViews操作） 在“Specification”选项卡的“Equation specification”文 本框中输入用OLS（普通最小二乘法）估计的方程。 在“Options”选项卡中，选中“Weighted LS/TSLS”复 选框，并在“Weighted”的文本框中输入加权序列的名 称，例如输入“w”。 加权序列“w ”用OLS估计模型 时得到的残差序列的绝对值的 倒数序列。填好后再单击 “确定”按钮
在“Equation specification”（方程设定）中列出方程的被 解释变量和所有解释变量（包括常数项），在 “Instrument list”（工具变量列表）中，列出工具变量名。
注意：工具变量的个数不能比被估计参数的个数少，否则广义矩估 计法（GMM）的估计量不可识别。同样，在这里常数项会被自动 加入工具变量列表中。
基本思路： 赋予每个观测值残差不同的权数，从而使得回归模型的随 机误差项具有同方差性。
EViews统计分析基础教程
一、加权最小二乘法（WLS）
1.异方差问题的解决
基本原理： 设一元线性方程为
yt =β0 +β1xt +μt 如果随机误t差项的方差Var(μt)与解释变量成比例关系，
即
Var(μt) = σt2 = f(xt)×σ2 说明随机误差项的方差与解释变量xt之间存在相关性，即存
EViews统计分析基础教程
三、两阶段最小二乘法（TSLS）
基本原理：
两阶段最小二乘法分两个阶段： 第一阶段:找到工具变量，用最小二乘估计法（OLS）对 模型中的每一解释变量与工具变量做回归； 第二阶段:用第一阶段的拟合值代替内生变量，对原方 程进行第二次回归，这次回归得到的系数就是用两阶段 最小二乘法得到的新估计值。
EViews统计分析基础教程
五、广义矩估计（GMM）
EViews基本操作： 选择主菜单栏中 “Object”|“New Object”|“Equation”选项， 或者选择“Quick”|“Estimate Equation” 选项，在 “Method”中选择“GMM”后弹出如下图所示的方程设 定对话框。
EViews统计分析基础教程
二、广义最小二乘法（GLS）
广义最小二乘法（Generalized Least Squared，GLS） 常用来对存在序列相关和异方差的模型进行估计。普通 最小二乘法（OLS）和加统计分析基础教程
二、广义最小二乘法（GLS）
在异方差问题。
EViews统计分析基础教程
一、加权最小二乘法（WLS）
1.异方差问题的解决
消除方法： 用
1 f
x 乘以一元线性方程的两端，得
i
1 f
x
i
yt = f β 0 + x
i
1
f x i
1
β 1 xt +
1
μt)2 = E(μt)2 = σ2 f x f x 从而，消除了异方差，随机误差项同方差。这时再用普通 最小二乘法（OLS）估计其参数，得到有效的β0，β1估 计量。 则，Var(
EViews统计分析基础教程
三、两阶段最小二乘法（TSLS）
EViews操作：
在上图的方程设定（Equation specification）的文本框中 列出解释变量和被解释变量， 在工具变量列表（Instrument list）的文本框中输入工具 变量。 在进行两阶段最小二乘估计时，方程中的工具变量数至 少要与估计系数相等。常数项常常用来做工具变量。
EViews统计分析基础教程
四、非线性最小二乘法（NLS）
非线性模型包括可线性化的非线性模型和不可线性化的 非线性模型。可线性化的模型是指该模型可以通过线性 化的处理变为线性模型，如一元二次方程，幂函数等。 例如： y =axb lny =lna+blnx 即 y﹡=a﹡+bx﹡ 并非所有的函数均可被线性化，能被线性化的可以继续 用OLS等线性回归模型适用的方法进行估计，不能被线 性化的模型就可以用非线性最小二乘法（Nonlinear Least Square，NLS）进行估计。
EViews统计分析基础教程
五、广义矩估计（GMM）
广义矩估计法（Generalized Method of Moments，GMM） 则可以不受模型假定的限制，它不要求随机扰动项一定 非序列相关，不存在异方差等，并且所得到的参数估计 值比用其他估计方法得到的参数估计值更与实际接近。 广义矩估计法（GMM）是一个大样本估计，其估计量 在大样本下有效，在小样本下无效。
EViews统计分析基础教程
三、两阶段最小二乘法（TSLS）
EViews操作：
选择主菜单栏中的“Object”| “New Object” | “Equation” 选项，或者选择“Quick”| “Estimate Equation” 选项，在 打开的方程对话框的“Method”种选择“TSLS”法，会得 到如下对话框。
i i i
f x μt) = E(
1
f x i
1
μt
1
EViews统计分析基础教程
一、加权最小二乘法（WLS）
1.异方差问题的解决
消除方法（EViews操作） （1）用最小二乘法（OLS）估计方程，得到残差序列； （2）根据残差序列计算出加权序列； （3）选择EViews主菜单栏中的“Quick”| “Estimate Equation”选项，弹出下图所示的对话框。 包括两个选项卡： （1）“Specification”选项 卡 （2）“Options”选项卡
EViews统计分析基础教程
二、广义最小二乘法（GLS）
基本原理： 再求模型(3)的滞后1期即(t-1)期的回归模型，并在两侧 同乘 yt-1= 0 + 1x1t-1 +2x2t-1 +…+kxkt-1+ ut-1 (4) 用（2）式与(4)相减，得 ut- yt-1 = 0 (1-)+1(x1t-x1t-1)+ …+k(xk-1- xkt-1) + vt (5) 令 yt* = yt - yt -1 xjt* = xjt -xjt -1, j = 1 , 2 , … k (6) 0* = 0 (1 - ) 则yt* = 0*+ 1 x1 t* + 2 x2 t* +… + k xk t* + vt 如果模型不存在异方差和序列相关，则使用广义最小二 乘法等于普通最小二乘法。
EViews统计分析基础教程
第6章 基本回归模型的OLS估计
重点内容：
• 加权最小二乘法（消除异方差）
• 广义最小二乘法（消除序列相关和异方差）
• 广义矩估计
EViews统计分析基础教程
一、加权最小二乘法（WLS）
1.异方差问题的解决
当线性回归模型出现异方差时，所得到的估计量是非有效 的。用加权最小二乘法（WLS）可以解决异方差问题。



EViews统计分析基础教程
四、非线性最小二乘法（NLS）
EViews操作： 选择主菜单栏中 “Object”|“New Object”|“Equation”选项， 或者选择“Quick”|“Estimate Equation” 选项，打开方程 设定对话框，在“Equation specification”中输入非线性模 型的表达式，如“y c 1/x”，即为双曲线的回归模型。 EViews软件会自动用非线性最小二乘法（NLS）进行估 计，因而建立方程时，只输入非线性表达式即可。例如 y =axb ，只需输入“y= c(1)*x^c(2)”即可。
基本原理：
通过变换原回归模型，使随机误差项消除自相关，进而 利用普通最小二乘法估计回归参数 。 设原回归模型是 yt = 0 + 1x1t + 2 x2t+…+ kxkt +ut (t = 1, 2, …, n )（1） 其中，ut具有一阶自回归形式 ut = ut-1 + vt （2） vt 满足线性回归模型的基本假定条件，把（2）式代入 （1）式中，得 yt = 0+1x1t+2x2t+…+0xkt+ut- 1 + vt （3）
EViews统计分析基础教程
五、广义矩估计（GMM）
基本原理： 广义矩估计是设定参数满足的一种理论关系。其原理是 选择参数估计尽可能接近理论上关系，把理论关系用样 本近似值代替；并且估计量的选择就是要最小化理论值 和实际值之间的加权距离。参数要满足的理论关系通常 是参数函数f(θ)与工具变量Zt之间的正则条件，即 E[f(θ)′Z]=0，θ是被估计参数 广义矩估计法（GMM）中估计量选择的标准是，使工 具变量与函数f(θ)之间的样本相关性越接近于0越好。